Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization for Hyperspectral Classification
Abstract
:1. Introduction
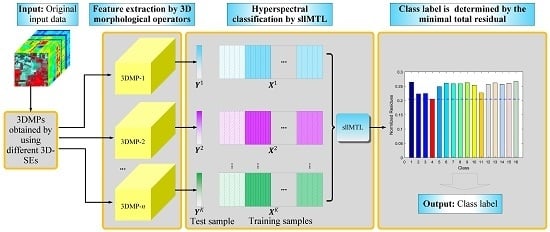
- 3D-MPs are adopted for feature extraction of the HSI cube. Compared to the vector/image-based methods, we respect the 3D nature of the HSI and take the HSI cube as a whole entity to simultaneously extract the spectral-spatial features. Different from the existing 3D-MPs-based method, we do not simply stack multiple 3D-MPs but fully exploit the spectral-spatial feature of each 3DMP in a novel MTL framework.
- sllMTL is proposed to simultaneously classify the 3D-MPs by taking each 3D-MP as the feature of a specific task. Compared to the existing MTL, the proposed sllMTL can capture both specificities and shared factors of the tasks by utilizing the sparse and low-rank constraints. Moreover, the Laplacian-like regularization can improve the classification performance further by making full use of the class label information.
2. Multiple Morphological Profiles Extracted by 3D Mathematical Morphology
3. Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization
| Algorithm 1: LADMAP for Solving the Optimization Problem (see Equation (5)) in the Proposed sllMTL Method |
2: while Convergence is not attained do 3: Fix the others and update the variable by Equation (12) 4: Fix the others and update the variable by Equation (13) 5: Fix the others and update the variable by Equation (15) 6: Update the Lagrange multipliers and by 7: Update the parameter by 8: Update t by 9: end while 10: Determine the class label of by Equation (16) |
4. Experiments
4.1. Dataset Description
- Indian Pines data: the first data was gathered by the National Aeronautics and Space Administration’s (NASA) Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor on 12 June 1992 over the Indian Pines test site in Northwest Indiana, and it consists of pixels and 220 spectral reflectance bands cover the wavelength range of 0.4–2.5 m. The number of bands is reduced to 200 by removing the noisy and water-vapor absorption bands (bands 104–108, 150–163, and 220). The spatial resolution is about 20 m per pixel. Figure 4 depicts the three-band false color composite image together with its corresponding ground truth. The data contains 16 classes of interest land-covers and 10366 labeled pixels ranging unbalanced from 20 to 2468, which poses a big challenge to the classification problem. Table 1 displays the detailed number of samples of each class, and the background color represents different classes of land-covers.
- University of Pavia data: the second dataset was captured by the Reflective Optics System Imaging Spectrometer (ROSIS) sensor on 8 July 2002 over an urban area surrounding the University of Pavia, Italy. It contains pixels with a spatial resolution of 1.3 m per pixel. The original dataset has 115 spectral channels with a coverage range from 0.43 to 0.86 m. 12 most noisy bands are removed before experiments, remaining 103 bands for experiments. 9 classes of interest are considered in this dataset. The color composite image, the ground truth data as well as the available training samples are depicted in Figure 5. As shown in Table 2, there are more than 900 pixels in each class, but the available training samples of each class are less than 600. In analogy to the Indian Pines data, the background color in Table 2 also agrees with that in Figure 5b,c.
- Salinas data: the third dataset was acquired by the AVIRIS sensor on 8 October 1998 over the Salinas Valley, Southern California, USA. There are 224 bands in the original dataset, and 24 bands (bands 108–112, 154–167, and 224) are removed for the water absorption. The size of each band is pixels with a spatial resolution of 3.7 m per pixel. The color composite image and the ground truth are plotted in Figure 6. This dataset contains 16 classes of ground truth, and the detailed number of samples in each class is listed in Table 3, whose background color corresponds to different classes of land-covers.
4.2. Experimental Design
4.3. Experimental Results
5. Discussion
5.1. Statistical Significance Analysis of the Results
5.2. Sensitivity Analysis of the Parameters
5.3. Influence Analysis of the 3D-SEs
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for Earth Observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef] [Green Version]
- Angelliaume, S.; Ceamanos, X.; Viallefont-Robinet, F.; Baqué, R.; Déliot, P.; Miegebielle, V. Hyperspectral and Radar airborne imagery over controlled release of oil at sea. Sensors 2017, 17, 1772. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Zhao, C.; Wang, J.; Jia, X.; Yang, G.; Song, X.; Feng, H. An improved combination of spectral and spatial features for vegetation classification in hyperspectral images. Remote Sens. 2017, 9, 261. [Google Scholar] [CrossRef]
- Schneider, S.; Murphy, R.J.; Melkumyan, A. Evaluating the performance of a new classifier-the GP-OAD: A comparison with existing methods for classifying rock type and mineralogy from hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2014, 98, 145–156. [Google Scholar] [CrossRef]
- Sun, B.; Kang, X.; Li, S.; Benediktsson, J.A. Random-walker-based collaborative learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 212–222. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Zhong, Y.; Jia, T.; Zhao, J.; Wang, X.; Jin, S. Spatial-spectral-emissivity land-cover classification fusing visible and thermal infrared hyperspectral imagery. Remote Sens. 2017, 9, 910. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Kuo, B.C.; Ho, H.H.; Li, C.H.; Hung, C.C.; Taur, J.S. A kernel-based feature selection method for SVM with RBF kernel for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 317–326. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, C.; You, D.; Zhang, Y.; Wang, S.; Zhang, Y. Representative multiple kernel learning for classification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2852–2865. [Google Scholar] [CrossRef]
- Gurram, P.; Kwon, H. Sparse kernel-based ensemble learning with fully optimized kernel parameters for hyperspectral classification problems. IEEE Trans. Geosci. Remote Sens. 2013, 51, 787–802. [Google Scholar] [CrossRef]
- Maulik, U.; Chakraborty, D. Learning with transductive SVM for semisupervised pixel classification of remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2013, 77, 66–78. [Google Scholar] [CrossRef]
- Wang, L.; Hao, S.; Wang, Q.; Wang, Y. Semi-supervised classification for hyperspectral imagery based on spatial-spectral label propagation. ISPRS J. Photogramm. Remote Sens. 2014, 97, 123–137. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.; Ganesh, A.; Sastry, S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Huang, Y.; Zhang, L. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2056–2065. [Google Scholar] [CrossRef]
- Srinivas, U.; Suo, Y.; Dao, M.; Monga, V.; Tran, T.D. Structured sparse priors for image classification. IEEE Trans. Image Process. 2015, 24, 1763–1776. [Google Scholar] [CrossRef] [PubMed]
- Dao, M.; Nguyen, N.H.; Nasrabadi, N.M.; Tran, T.D. Collaborative multi-sensor classification via sparsity-based representation. IEEE Trans. Signal Process. 2016, 64, 2400–2415. [Google Scholar] [CrossRef]
- Bian, X.; Chen, C.; Xu, Y.; Du, Q. Robust hyperspectral image classification by multi-layer spatial-spectral sparse representations. Remote Sens. 2016, 8, 985. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Fu, W.; Fang, L. Multiscale superpixel-based sparse representation for hyperspectral image classification. Remote Sens. 2017, 9, 139. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Su, H.; Zhou, S. Discriminative sparse representation for hyperspectral image classification: a semi-supervised perspective. Remote Sens. 2017, 9, 386. [Google Scholar] [CrossRef]
- Dao, M.; Kwan, C.; Koperski, K.; Marchisio, G. A joint sparsity approach to tunnel activity monitoring using high resolution satellite images. In Proceedings of the IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 322–328. [Google Scholar]
- Ul Haq, Q.S.; Tao, L.; Sun, F.; Yang, S. A fast and robust sparse approach for hyperspectral data classification using a few labeled samples. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2287–2302. [Google Scholar] [CrossRef]
- He, Z.; Wang, Q.; Shen, Y.; Sun, M. Kernel sparse multitask learning for hyperspectral image classification with empirical mode decomposition and morphological wavelet-based features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5150–5163. [Google Scholar]
- Li, J.; Zhang, H.; Zhang, L.; Huang, X.; Zhang, L. Joint collaborative representation with multitask learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5923–5936. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L. A nonlinear multiple feature learning classifier for hyperspectral images with limited training samples. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 2728–2738. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, K.; Du, B.; Zhang, L.; Hu, X. Hyperspectral target detection via adaptive joint sparse representation and multi-task learning with locality information. Remote Sens. 2017, 9, 482. [Google Scholar] [CrossRef]
- Jia, S.; Deng, B.; Zhu, J.; Jia, X.; Li, Q. Superpixel-based multitask learning framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2575–2588. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Benediktsson, J.; Palmason, J.; Sveinsson, J. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Hou, B.; Huang, T.; Jiao, L. Spectral-spatial classification of hyperspectral data using 3-D morphological profile. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2364–2368. [Google Scholar]
- Lin, Z.; Liu, R.; Su, Z. Linearized alternating direction method with adaptive penalty for low-rank representation. In Advances in Neural Information Processing Systems 24 (NIPS 2011); Curran Associates, Inc.: Granada, Spain, 2011; pp. 612–620. [Google Scholar]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral image classification based on structured sparse logistic regression and three-dimensional wavelet texture features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2276–2291. [Google Scholar] [CrossRef]
















 |
 |
 |
| Class | sllMTL | 3D-MPs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spec | EMP | 3D-DWT | 3D-MPs | SVM | SVMCK | MTL | sllMTL | sllMTL | sllMTL | ||
| 1 | 25.38 | 59.13 | 63.46 | 88.46 | 93.27 | 93.27 | 70.77 | 70.43 | 73.72 | 88.46 | |
| 2 | 63.90 | 80.36 | 82.52 | 70.68 | 57.49 | 61.79 | 78.27 | 77.03 | 74.44 | 70.68 | |
| 3 | 48.85 | 71.70 | 70.29 | 78.42 | 87.79 | 85.83 | 75.61 | 66.39 | 73.09 | 78.42 | |
| 4 | 26.54 | 73.86 | 74.68 | 86.15 | 69.96 | 76.45 | 53.46 | 72.35 | 73.30 | 86.15 | |
| 5 | 73.70 | 72.23 | 73.81 | 74.59 | 65.73 | 67.30 | 75.94 | 63.08 | 72.49 | 74.59 | |
| 6 | 88.44 | 91.90 | 92.35 | 95.81 | 89.53 | 90.37 | 93.25 | 90.12 | 92.11 | 95.81 | |
| 7 | 53.75 | 100.00 | 100.00 | 100.00 | 95.42 | 100.00 | 100.00 | 99.48 | 100.00 | 100.00 | |
| 8 | 92.98 | 99.20 | 99.20 | 99.17 | 98.62 | 98.60 | 97.19 | 99.07 | 99.17 | 99.17 | |
| 9 | 46.67 | 95.14 | 93.75 | 88.89 | 47.22 | 80.00 | 70.56 | 84.03 | 87.04 | 88.89 | |
| 10 | 64.06 | 75.89 | 76.62 | 89.98 | 70.52 | 75.72 | 75.82 | 78.05 | 82.64 | 89.98 | |
| 11 | 73.24 | 91.17 | 91.21 | 94.35 | 90.23 | 90.69 | 93.78 | 91.84 | 96.64 | 94.35 | |
| 12 | 36.39 | 74.63 | 74.79 | 86.33 | 60.02 | 63.82 | 65.85 | 74.16 | 74.30 | 86.33 | |
| 13 | 94.16 | 99.46 | 99.46 | 99.52 | 97.94 | 98.42 | 93.21 | 98.50 | 98.41 | 99.52 | |
| 14 | 92.58 | 97.45 | 97.38 | 99.53 | 98.17 | 98.24 | 97.66 | 97.10 | 99.17 | 99.53 | |
| 15 | 26.81 | 82.18 | 83.18 | 85.11 | 80.72 | 83.38 | 70.19 | 78.32 | 84.13 | 85.11 | |
| 16 | 50.00 | 99.73 | 99.56 | 100.00 | 91.72 | 95.70 | 89.57 | 99.33 | 98.57 | 100.00 | |
| OA | 68.54 | 85.40 | 85.84 | 88.55 | 81.35 | 83.11 | 84.62 | 84.07 | 86.93 | 88.55 | |
| AA | 59.84 | 85.25 | 85.77 | 89.81 | 80.90 | 84.97 | 81.32 | 83.71 | 86.20 | 89.81 | |
| 63.92 | 83.28 | 83.79 | 86.90 | 78.73 | 80.76 | 82.35 | 81.73 | 85.00 | 86.90 | ||
| Class | sllMTL | 3D-MPs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spec | EMP | 3D-DWT | 3D-MPs | SVM | SVMCK | MTL | sllMTL | sllMTL | sllMTL | ||
| 1 | 68.90 | 87.91 | 88.13 | 92.04 | 86.62 | 89.64 | 87.20 | 86.07 | 91.25 | 92.04 | |
| 2 | 77.85 | 67.59 | 70.63 | 69.31 | 69.31 | 68.13 | 73.70 | 65.15 | 67.74 | 69.31 | |
| 3 | 51.60 | 65.60 | 73.70 | 82.99 | 72.46 | 74.85 | 73.56 | 66.22 | 71.80 | 82.99 | |
| 4 | 86.85 | 63.94 | 82.21 | 97.81 | 72.06 | 83.58 | 80.29 | 79.96 | 88.19 | 97.81 | |
| 5 | 72.19 | 99.93 | 99.93 | 79.33 | 59.70 | 76.58 | 60.59 | 99.85 | 98.74 | 79.33 | |
| 6 | 38.38 | 72.94 | 61.13 | 76.72 | 55.90 | 63.59 | 58.62 | 75.98 | 69.85 | 76.72 | |
| 7 | 89.77 | 93.08 | 96.84 | 93.01 | 96.69 | 96.54 | 91.20 | 95.34 | 94.74 | 93.01 | |
| 8 | 41.01 | 78.79 | 61.68 | 74.99 | 63.25 | 63.82 | 69.07 | 83.41 | 74.96 | 74.99 | |
| 9 | 59.13 | 97.99 | 95.67 | 99.26 | 96.09 | 98.63 | 96.20 | 99.47 | 99.37 | 99.26 | |
| OA | 67.79 | 74.45 | 74.73 | 78.62 | 71.39 | 73.82 | 74.71 | 75.14 | 76.43 | 78.62 | |
| AA | 65.08 | 80.86 | 81.10 | 85.05 | 74.68 | 79.48 | 76.71 | 83.49 | 84.07 | 85.05 | |
| 58.03 | 67.42 | 67.54 | 73.02 | 62.68 | 66.36 | 66.74 | 68.67 | 70.02 | 73.02 | ||
| Class | sllMTL | 3D-MPs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spec | EMP | 3D-DWT | 3D-MPs | SVM | SVMCK | MTL | sllMTL | sllMTL | sllMTL | ||
| 1 | 97.48 | 98.54 | 99.35 | 99.90 | 99.45 | 98.09 | 98.29 | 98.64 | 99.30 | 99.90 | |
| 2 | 99.78 | 99.16 | 99.02 | 100.00 | 97.97 | 99.13 | 99.70 | 99.54 | 99.78 | 100.00 | |
| 3 | 98.01 | 98.11 | 97.14 | 99.54 | 98.77 | 97.65 | 98.62 | 98.21 | 99.64 | 99.54 | |
| 4 | 98.12 | 98.99 | 99.35 | 99.71 | 98.70 | 97.61 | 99.28 | 98.70 | 98.99 | 99.71 | |
| 5 | 98.53 | 97.81 | 96.57 | 98.83 | 96.57 | 96.34 | 97.51 | 96.83 | 98.30 | 98.83 | |
| 6 | 99.95 | 99.95 | 99.13 | 99.97 | 99.16 | 98.72 | 99.72 | 99.92 | 99.92 | 99.97 | |
| 7 | 99.72 | 98.50 | 99.41 | 99.86 | 95.96 | 99.27 | 99.63 | 99.69 | 99.77 | 99.86 | |
| 8 | 89.56 | 88.19 | 91.49 | 93.85 | 83.82 | 87.42 | 91.76 | 90.10 | 93.37 | 93.85 | |
| 9 | 99.45 | 99.67 | 99.25 | 99.90 | 99.59 | 99.09 | 99.35 | 99.54 | 99.79 | 99.90 | |
| 10 | 89.65 | 95.10 | 93.93 | 98.34 | 87.70 | 92.70 | 96.21 | 96.09 | 95.93 | 98.34 | |
| 11 | 91.49 | 98.01 | 94.99 | 99.62 | 90.26 | 95.65 | 88.55 | 92.90 | 96.78 | 99.62 | |
| 12 | 99.58 | 99.42 | 99.79 | 100.00 | 99.63 | 99.58 | 99.84 | 99.84 | 99.79 | 100.00 | |
| 13 | 98.45 | 98.34 | 99.12 | 99.45 | 97.90 | 98.12 | 98.23 | 94.81 | 99.45 | 99.45 | |
| 14 | 94.81 | 95.85 | 97.26 | 99.34 | 96.79 | 93.67 | 93.86 | 97.92 | 97.54 | 99.34 | |
| 15 | 57.05 | 85.24 | 83.16 | 86.46 | 82.34 | 81.26 | 80.93 | 81.14 | 81.42 | 86.46 | |
| 16 | 98.04 | 97.26 | 98.49 | 99.22 | 96.98 | 96.48 | 98.27 | 98.64 | 97.54 | 99.22 | |
| OA | 90.67 | 94.54 | 94.80 | 96.64 | 92.33 | 93.34 | 94.66 | 94.43 | 95.46 | 96.64 | |
| AA | 94.35 | 96.76 | 96.71 | 98.37 | 95.10 | 95.67 | 96.24 | 96.39 | 97.33 | 98.37 | |
| 89.57 | 93.93 | 94.20 | 96.25 | 91.45 | 92.59 | 94.05 | 93.79 | 94.94 | 96.25 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wang, Y.; Hu, J. Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization for Hyperspectral Classification. Remote Sens. 2018, 10, 322. https://doi.org/10.3390/rs10020322
He Z, Wang Y, Hu J. Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization for Hyperspectral Classification. Remote Sensing. 2018; 10(2):322. https://doi.org/10.3390/rs10020322
Chicago/Turabian StyleHe, Zhi, Yiwen Wang, and Jie Hu. 2018. "Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization for Hyperspectral Classification" Remote Sensing 10, no. 2: 322. https://doi.org/10.3390/rs10020322
APA StyleHe, Z., Wang, Y., & Hu, J. (2018). Joint Sparse and Low-Rank Multitask Learning with Laplacian-Like Regularization for Hyperspectral Classification. Remote Sensing, 10(2), 322. https://doi.org/10.3390/rs10020322