Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal
Abstract
:1. Introduction
- (1)
- Fully considering the latent priors of stripes, we formulate an sparse model to depict the intrinsically sparse characteristic of the stripes.
- (2)
- We solve the non-convex model by a designed PADMM based algorithm which the corresponding theoretical analysis is given by this paper (see Appendix A).
- (3)
- The proposed method outperforms recent several competitive image destriping methods.
2. Related Work
2.1. Destriping Problem Formulation
2.2. UTV for Remote Sensing Image Destriping
3. The Proposed Method
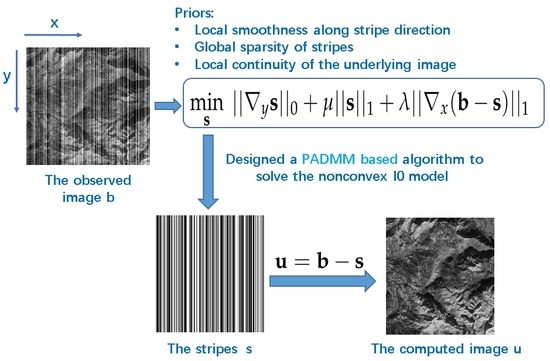
3.1. The Proposed Model
3.1.1. Local Smoothness Along Stripe Direction
3.1.2. Local Continuity of the Underlying Image
3.1.3. Global Sparsity of Stripes
3.2. The Solution
3.3. PADMM Based Algorithm
| Algorithm 1 The algorithm for model in Equation (13) |
| Input: The observed image (with stripes), the parameters , the constant , the maximum number of iterations , and the calculation accuracy . Output: The stripes Initialize: (1) , , , rho← 1 While rho> tol and k < (2) (3) Solve by Equation (21) (4) Solve by Equation (23) (5) Solve by Equation (25) (6) Solve by Equation (27) (7) Solve by Equation (29) (8) Update the multipliers by Equation (30) (9) Calculate . Endwhile |
4. Experiment Results
4.1. Simulated Experiments
4.1.1. Periodic Stripes
4.1.2. Nonperiodic Stripes
4.1.3. Averagely Quantitative Performance on 32 Test Images
4.2. Real Experiments
4.3. More Analysis
4.3.1. Qualitative Analysis
4.3.2. The Influence of Different Regularization Terms in the Proposed Model
5. Discussion
5.1. Parameter Value Selection
5.2. Limitation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Convergence of the Proposed Method
- (i)
- According to the limit of and the update formula of the multipliers , we can get
- (ii)
- According to the limit of , , and the subproblem of in Equation (18) , we can getBy the first optimality condition of , we have
- (iii)
- According to the limit of , and the subproblem of in Equation (22), we can getBy the first optimality condition of , we have
- (iv)
- According to the limit of , and the subproblem of in Equation (24), we can getBy the first optimality condition of , we have
- (v)
- According to the limit of , and the subproblem of in Equation (26), we can getBy the first optimality condition of , we have
- (vi)
- According to the limit of and the update formula of subproblem of in Equation (28), we have the first optimality condition of is
References
- Chen, J.S.; Shao, Y.; Guo, H.D.; Wang, W.M.; Zhu, B.Q. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Pal, M.K.; Porwal, A. Destriping of Hyperion images using low-pass-filter and local-brightness-normalization. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar]
- Gadallah, F.L.; Csillag, F.; Smith, E.J.M. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Woodham, R.J. Destriping Landsat MSS images by histogram modification. Comput. Graph. Image Process. 1979, 10, 69–83. [Google Scholar] [CrossRef]
- Weinreb, M.P.; Xie, R.; Lienesch, J.H.; Crosby, D.S. Destriping GOES images by matching empirical distribution functions. Remote Sens. Environ. 1989, 29, 185–195. [Google Scholar] [CrossRef]
- Wegener, M. Destriping multiple sensor imagery by improved histogram matching. Int. J. Remote Sens. 1990, 11, 859–875. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Restoration of Aqua MODIS band 6 using histogram matching and local least squares fitting. IEEE Trans. Geosci. Remote Sens. 2009, 47, 613–627. [Google Scholar] [CrossRef]
- Sun, L.X.; Neville, R.; Staenz, K.; White, H.P. Automatic destriping of Hyperion imagery based on spectral moment matching. Can. J. Remote Sens. 2008, 34, S68–S81. [Google Scholar] [CrossRef]
- Shen, H.F.; Jiang, W.; Zhang, H.Y.; Zhang, L.P. A piece-wise approach to removing the nonlinear and irregular stripes in MODIS data. Int. J. Remote Sens. 2014, 35, 44–53. [Google Scholar] [CrossRef]
- Fehrenbach, J.; Weiss, P.; Lorenzo, C. Variational algorithms to remove stationary noise: applications to microscopy imaging. IEEE Trans. Image Process. 2012, 21, 4420–4430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fehrenbach, J.; Weiss, P. Processing stationary noise: model and parameter selection in variational methods. SIAM J. Imaging Sci. 2014, 7, 613–640. [Google Scholar] [CrossRef]
- Escande, P.; Weiss, P.; Zhang, W.X. A variational model for multiplicative structured noise removal. J. Math. Imaging Vis. 2017, 57, 43–55. [Google Scholar] [CrossRef]
- Shen, H.F.; Zhang, L.P. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; Zhao, X.L.; Deng, L.J.; Huang, J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sens. 2017, 9, 559. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Zhang, H.Y.; He, W.; Zhang, L.P.; Shen, H.F.; Yuan, Q.Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Zhou, G.; Fang, H.Z.; Yan, L.X.; Zhang, T.X.; Hu, J. Removal of stripe noise with spatially adaptive unidirectional total variation. Opt. Int. J. Light Electron Opt. 2014, 125, 2756–2762. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.L.; Liu, S.Y.; Liu, T.T.; Chang, Y. Destriping algorithm with L0 sparsity prior for remote sensing images. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 2295–2299. [Google Scholar]
- Chang, Y.; Yan, L.X.; Fang, H.Z.; Liu, H. Simultaneous destriping and denoising for remote sensing images with unidirectional total variation and sparse representation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1051–1055. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.X.; Fang, H.Z.; Luo, C.N. Anisotropic Spectral-Spatial Total Variation Model for Multispectral Remote Sensing Image Destriping. IEEE Trans. Image Process. 2015, 24, 1852–1866. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Zhang, H.Y.; Zhang, L.P.; Shen, H.F. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Zorzi, M.; Chiuso, A. Sparse plus low rank network identification: A nonparametric approach. Automatica 2017, 76, 355–366. [Google Scholar] [CrossRef]
- Zorzi, M.; Sepulchre, R. AR identification of latent-variable graphical models. IEEE Trans. Autom. Control 2016, 61, 2327–2340. [Google Scholar] [CrossRef]
- Liu, X.X.; Lu, X.L.; Shen, H.F.; Yuan, Q.Q.; Jiao, Y.L.; Zhang, L.P. Stripe Noise Separation and Removal in Remote Sensing Images by Consideration of the Global Sparsity and Local Variational Properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote Sensing Image Stripe Noise Removal: From Image Decomposition Perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.Z.; Selesnick, I.W.; Lv, X.G.; Chen, P.Y. Image restoration using total variation with overlapping group sparsity, Information Sciences. Inf. Sci. 2015, 295, 232–246. [Google Scholar] [CrossRef]
- Mei, J.J.; Dong, Y.Q.; Huang, T.Z.; Yin, W.T. Cauchy noise removal by nonconvex ADMM with convergence guarantees. J. Sci. Comput. 2018, 74, 743–766. [Google Scholar] [CrossRef]
- Ji, T.Y.; Huang, T.Z.; Zhao, X.L.; Ma, T.H.; Deng, L.J. A non-convex tensor rank approximation for tensor completion. Appl. Math. Model. 2017, 48, 410–422. [Google Scholar] [CrossRef]
- Carfantan, H.; Idier, J. Statistical linear destriping of satellite-based pushbroom-type images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1860–1871. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Zhao, X.L.; Wang, F.; Huang, T.Z.; Ng, M.K.; Plemmons, R.J. Deblurring and sparse unmixing for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4045–4058. [Google Scholar] [CrossRef]
- Ma, T.H.; Huang, T.Z.; Zhao, X.L.; Lou, Y.F. Image Deblurring With an Inaccurate Blur Kernel Using a Group-Based Low-Rank Image Prior. Inf. Sci. 2017, 408, 213–233. [Google Scholar] [CrossRef]
- Getreuer, P. Total variation inpainting using split Bregman. Image Process. Line 2012, 2, 147–157. [Google Scholar] [CrossRef]
- Yuan, G.Z.; Ghanem, B. l0TV: A new method for image restoration in the presence of impulse noise. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5369–5377. [Google Scholar]
- Shen, H.F.; Li, X.H.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.F. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Dong, B.; Zhang, Y. An efficient algorithm for ℓ0 minimization in wavelet frame based image restoration. J. Sci. Comput. 2013, 54, 350–368. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, T.Z.; Ma, T.H.; Zhao, X.L. Cartoon-texture image decomposition via non-convex low-rank texture regularization. J. Frankl. Inst. 2017, 354, 3170–3187. [Google Scholar] [CrossRef]
- Lu, Z.S.; Zhang, Y. Sparse approximation via penalty decomposition methods. SIAM J. Optim. 2013, 23, 2448–2478. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assesment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- He, B.S.; Yuan, X.M. On the O(1/n) Convergence Rate of the Douglas Rachford Alternating Direction Method. SIAM J. Numer. Anal. 2012, 50, 700–709. [Google Scholar] [CrossRef]
- Deng, W.; Yin, W.T. On the global and linear convergence of the generalized alternating direction method of multipliers. J. Sci. Comput. 2016, 663, 889–916. [Google Scholar] [CrossRef]
- Wen, Z.W.; Yang, C.; Liu, X.; Marchesini, S. Alternating direction methods for classical and ptychographic phase retrieval. Inverse Probl. 2012, 28, 115010. [Google Scholar] [CrossRef]
- Fazel, M.; Pong, T.K.; Sun, D.F.; Tseng, P. Hankel matrix rank minimization with applications to system identification and realization. SIAM J. Matrix Anal. Appl. 2013, 34, 946–977. [Google Scholar] [CrossRef]














| Images | (a) | (b) | (c) | (d) | (e) | (f) | |
|---|---|---|---|---|---|---|---|
| ReErr | WFAF | 0.1588 | 0.2828 | 0.2519 | 0.2468 | 0.2386 | 0.2574 |
| SLD | 0.0874 | 0.1670 | 0.1723 | 0.1664 | 0.1330 | 0.1346 | |
| UTV | 0.0831 | 0.1542 | 0.2371 | 0.1818 | 0.1314 | 0.1375 | |
| GSLV | 0.0867 | 0.1030 | 0.2385 | 0.1926 | 0.0912 | 0.1654 | |
| LRSID | 0.0917 | 0.1884 | 0.2731 | 0.2125 | 0.1450 | 0.1897 | |
| Ours | 0.0193 | 0.0693 | 0.0365 | 0.0892 | 0.0304 | 0.0813 | |
| PSNR | WFAF | 37.1239 | 21.3097 | 33.1166 | 28.6960 | 24.5539 | 28.1562 |
| SLD | 42.3121 | 25.8878 | 36.4164 | 32.1200 | 29.6283 | 33.7867 | |
| UTV | 42.7463 | 26.5787 | 33.6413 | 31.3504 | 29.7370 | 33.6047 | |
| GSLV | 42.3798 | 30.0798 | 33.5899 | 30.8506 | 32.9031 | 31.9996 | |
| LRSID | 40.8345 | 24.7115 | 32.8728 | 30.4638 | 28.9817 | 31.6380 | |
| Ours | 55.4503 | 33.5287 | 49.8954 | 38.1697 | 42.4454 | 38.1677 |
| Intensity | Intensity = 10 | Intensity = 50 | Intensity = 100 | ||||
|---|---|---|---|---|---|---|---|
| Ratio | r = 0.2 | r = 0.6 | r = 0.2 | r = 0.6 | r = 0.2 | r = 0.6 | |
| PSNR | WFAF | 41.400 ± 3.601 | 41.702 ± 3.870 | 37.160 ± 1.975 | 37.553 ± 1.975 | 32.196 ± 1.457 | 32.501 ± 1.732 |
| SLD | 42.037 ± 2.927 | 41.048 ± 2.909 | 41.710 ± 2.930 | 41.957 ± 2.928 | 40.614 ± 2.549 | 41.644 ± 2.836 | |
| UTV | 42.030 ± 3.229 | 41.032 ± 2.886 | 40.920 ± 2.773 | 43.086 ± 2.298 | 41.470 ± 3.385 | 41.058 ± 3.299 | |
| GSLV | 42.552 ± 2.955 | 42.630 ± 2.886 | 42.202 ± 3.058 | 43.533 ± 2.856 | 43.431 ± 3.091 | 43.801 ± 2.705 | |
| LRSID | 43.948 ± 2.104 | 42.775 ± 2.010 | 42.308 ± 2.169 | 44.548 ± 1.976 | 43.779 ± 2.500 | 44.035 ± 2.014 | |
| Ours | 52.918 ± 4.074 | 49.497 ± 3.956 | 52.853 ± 4.910 | 49.212 ± 4.390 | 52.854 ± 4.902 | 49.182 ± 4.368 | |
| SSIM | WFAF | 0.9934 ± 0.0058 | 0.9936 ± 0.0062 | 0.9887 ± 0.0084 | 0.9905 ± 0.0078 | 0.9818 ± 0.0103 | 0.9847 ± 0.0085 |
| SLD | 0.9966 ± 0.0029 | 0.9966 ± 0.0029 | 0.9965 ± 0.0031 | 0.9965 ± 0.0032 | 0.9962 ± 0.0033 | 0.9964 ± 0.0037 | |
| UTV | 0.9959 ± 0.0027 | 0.9959 ± 0.0027 | 0.9911 ± 0.0025 | 0.9928 ± 0.0023 | 0.9954 ± 0.0024 | 0.9937 ± 0.0076 | |
| GSLV | 0.9991 ± 0.0077 | 0.9968 ± 0.0076 | 0.9916 ± 0.0079 | 0.9903 ± 0.0082 | 0.9966 ± 0.0085 | 0.9969 ± 0.0053 | |
| LRSID | 0.9990 ± 0.0107 | 0.9945 ± 0.0056 | 0.9932 ± 0.0044 | 0.9947 ± 0.0032 | 0.9936 ± 0.0047 | 0.9957 ± 0.0031 | |
| Ours | 0.9994 ± 0.0007 | 0.9987 ± 0.0011 | 0.9994 ± 0.0013 | 0.9986 ± 0.0016 | 0.9994 ± 0.0062 | 0.9986 ± 0.0019 | |
| Intensity | Intensity = 10 | Intensity = 50 | Intensity = 100 | ||||
|---|---|---|---|---|---|---|---|
| Ratio | r = 0.2 | r = 0.6 | r = 0.2 | r = 0.6 | r = 0.2 | r = 0.6 | |
| PSNR | WFAF | 40.971 ± 2.523 | 39.372 ± 2.249 | 30.536 ± 1.508 | 37.609 ± 2.263 | 24.849 ± 1.573 | 22.594 ± 1.541 |
| SLD | 41.476 ± 2.592 | 40.935 ± 2.201 | 35.964 ± 1.510 | 42.007 ± 3.020 | 30.963 ± 1.414 | 28.403 ± 1.729 | |
| UTV | 41.153 ± 2.880 | 38.615 ± 2.041 | 35.648 ± 1.527 | 42.505 ± 3.010 | 31.055 ± 4.687 | 31.599 ± 2.578 | |
| GSLV | 42.282 ± 2.359 | 39.018 ± 1.654 | 41.985 ± 1.239 | 39.838 ± 2.903 | 36.184 ± 1.399 | 35.408 ± 2.472 | |
| LRSID | 42.672 ± 1.418 | 39.034 ± 1.302 | 42.814 ± 1.349 | 40.497 ± 2.024 | 37.779 ± 1.212 | 33.559 ± 1.132 | |
| Ours | 48.801 ± 3.985 | 44.700 ± 3.784 | 49.057 ± 4.791 | 49.057 ± 4.492 | 44.365 ± 5.106 | 39.452 ± 4.494 | |
| SSIM | WFAF | 0.9925 ± 0.0056 | 0.9903 ± 0.0069 | 0.9744 ± 0.0104 | 0.9905 ± 0.0081 | 0.9364 ± 0.0207 | 0.9029 ± 0.0565 |
| SLD | 0.9965 ± 0.0031 | 0.9952 ± 0.0031 | 0.9950 ± 0.0041 | 0.9964 ± 0.0032 | 0.9907 ± 0.0060 | 0.9823 ± 0.0142 | |
| UTV | 0.9958 ± 0.0029 | 0.9934 ± 0.0052 | 0.9937 ± 0.0042 | 0.9914 ± 0.0056 | 0.9886 ± 0.0193 | 0.9851 ± 0.0122 | |
| GSLV | 0.9982 ± 0.0016 | 0.9917 ± 0.0042 | 0.9962 ± 0.0101 | 0.9967 ± 0.0088 | 0.9956 ± 0.0091 | 0.9933 ± 0.0152 | |
| LRSID | 0.9983 ± 0.0032 | 0.9934 ± 0.0113 | 0.9891 ± 0.0070 | 0.9962 ± 0.0042 | 0.9975 ± 0.0091 | 0.9924 ± 0.0402 | |
| Ours | 0.9991 ± 0.0006 | 0.9956 ± 0.0035 | 0.9990 ± 0.0010 | 0.9986 ± 0.0016 | 0.9979 ± 0.0012 | 0.9942 ± 0.0042 | |
| Images | Index | WFAF | SLD | UTV | GSLV | LRSID | Ours | |
|---|---|---|---|---|---|---|---|---|
| (a) | MICV | 4.7759 | 4.9274 | 6.8851 | 5.3955 | 7.4612 | 5.4162 | |
| MMRD (%) | 0.0078 | 0.0446 | 0.1646 | 0.1199 | 0.1590 | 0.0945 | ||
| (b) | MICV | 5.5871 | 5.5740 | 8.9350 | 6.4436 | 7.5592 | 7.4144 | |
| MMRD (%) | 0.0405 | 0.0377 | 0.1142 | 0.0695 | 0.0900 | 0.0662 | ||
| (c) | MICV | 3.9619 | 3.9940 | 4.3038 | 4.2884 | 4.0437 | 4.9604 | |
| MMRD (%) | 0.0286 | 0.0271 | 0.0276 | 0.0258 | 0.0385 | 0.0243 | ||
| (d) | MICV | 1.7057 | 1.6720 | 3.2297 | 2.2237 | 3.5039 | 2.6574 | |
| MMRD (%) | 0.3600 | 0.3785 | 0.1707 | 0.0876 | 0.2250 | 0.0262 | ||
| (e) | MICV | 0.8673 | 0.8533 | 0.8849 | 0.8786 | 0.8955 | 0.9017 | |
| MMRD (%) | 0.0328 | 0.0311 | 0.0432 | 0.0312 | 0.0265 | 0.0264 | ||
| (f) | MICV | 13.5619 | 13.2952 | 16.1001 | 16.5111 | 13.6906 | 16.7897 | |
| MMRD (%) | 0.0196 | 0.0210 | 0.0214 | 0.0190 | 0.0250 | 0.0176 |
| Image Size | WFAF | SLD | UTV | GSLV | LRSID | Ours | |
|---|---|---|---|---|---|---|---|
| 300 × 300 | 0.2274 | 0.0466 | 0.2745 | 1.1442 | 4.2581 | 6.6541 | |
| 400 × 400 | 0.2603 | 0.0650 | 0.5711 | 1.7004 | 8.5212 | 15.2448 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, H.-X.; Huang, T.-Z.; Deng, L.-J.; Zhao, X.-L.; Huang, J. Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal. Remote Sens. 2018, 10, 361. https://doi.org/10.3390/rs10030361
Dou H-X, Huang T-Z, Deng L-J, Zhao X-L, Huang J. Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal. Remote Sensing. 2018; 10(3):361. https://doi.org/10.3390/rs10030361
Chicago/Turabian StyleDou, Hong-Xia, Ting-Zhu Huang, Liang-Jian Deng, Xi-Le Zhao, and Jie Huang. 2018. "Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal" Remote Sensing 10, no. 3: 361. https://doi.org/10.3390/rs10030361
APA StyleDou, H. -X., Huang, T. -Z., Deng, L. -J., Zhao, X. -L., & Huang, J. (2018). Directional ℓ0 Sparse Modeling for Image Stripe Noise Removal. Remote Sensing, 10(3), 361. https://doi.org/10.3390/rs10030361