Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK
Abstract
:1. Introduction
2. The Forth Road Bridge and Its Monitoring System, GeoSHM
3. Data Processing Strategy
3.1. GNSS Data Pre-Processing
3.2. The Processing of the Vertical Deformation Time Series
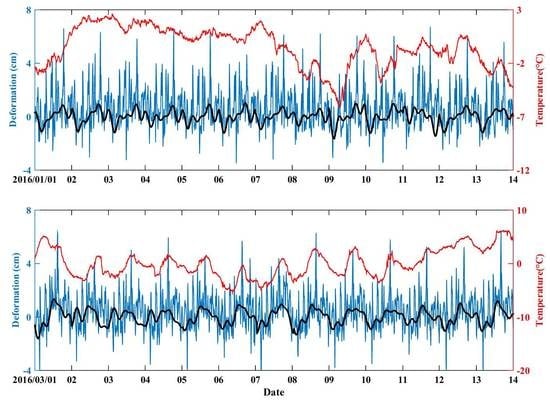
4. Results
4.1. Annual Signal Analysis
4.2. Daily Signal Analysis
4.3. Noise Characteristic Analysis
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Estes, A.C. Bridge Maintenance, Safety Management, Health Monitoring and Informatics. Struct. Infrastruct. Eng. 2009, 5, 341. [Google Scholar] [CrossRef]
- Larocca, A.P.C.; Schaal, R.E.; Santos, M.C.; Langley, R.B. Analyzing the dynamic behavior of suspension bridge towers using GPS. In Proceedings of the 19th International Technical Meeting of the ION Satellite Division—ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Chen, Z.; Zhou, X.; Wang, X.; Dong, L.; Qian, Y. Deployment of a Smart Structural Health Monitoring System for Long-Span Arch Bridges: A Review and a Case Study. Sensors 2017, 17, 2151. [Google Scholar] [CrossRef] [PubMed]
- Meng, X. Real-Time Deformation Monitoring of Bridges Using GPS/Accelerometers. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2002. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Laboratory: Los Alamos, NM, USA, 1996.
- Ashkenazi, V.; Roberts, G.W. Experimental monitoring of the Humber Bridge using GPS. Proc. Inst. Civ. Eng.-Civ. Eng. 1997, 120, 177–182. [Google Scholar] [CrossRef]
- Ren, W.-X.; Harik, I.E.; Blandford, G.E.; Lenett, M.; Baseheart, T.M. Roebling suspension bridge. II: Ambient testing and live-load response. J. Bridge Eng. 2004, 9, 119–126. [Google Scholar] [CrossRef]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Bao, Y.; Beck, J.L.; Li, H. Compressive sampling for accelerometer signals in structural health monitoring. Struct. Health Monit. 2011, 10, 235–246. [Google Scholar]
- Zonta, D.; Esposito, P.; Pozzi, M.; Molignoni, M.; Zandonini, R.; Ming, W.; Daniele, I.; Daniele, P.; Glisic, B. Monitoring load redistribution in a cable-stayed bridge. In Proceedings of the 5th European Conference on Structural Control, Genova, Italy, 18–20 June 2012. [Google Scholar]
- Curry, S.; Griffioen, P. Real-Time Kinematic GPS for Surveying: Centimeters in Seconds. In Proceedings of the American Society for Photogrammetry and Remote Sensing and America Congress on Surveying and Mapping Annual Convention, New Orleans, LA, USA, 15–18 February 1993; p. 109. [Google Scholar]
- Meng, X.; Roberts, G.W.; Dodson, A.H.; Ince, S.; Waugh, S. GNSS for structural deformation and deflection monitoring: Implementation and data analysis. In Proceedings of the 3rd IAG/12th FIG symposium, Baden, Austria, 22–24 May 2006. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System: Theory and Practice; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Brown, C.J.; Roberts, G.W.; Meng, X. A Tale of Five Bridges; the use of GNSS for Monitoring the Deflections of Bridges. J. Appl. Geod. 2014, 8, 241–264. [Google Scholar]
- Celebi, M.; Sanli, A. GPS in pioneering dynamic monitoring of long-period structures. Earthq. Spectra 2002, 18, 47–61. [Google Scholar] [CrossRef]
- Yang, J.; Li, J.B.; Lin, G. A simple approach to integration of acceleration data for dynamic soil–structure interaction analysis. Soil Dyn. Earthq. Eng. 2006, 26, 725–734. [Google Scholar] [CrossRef]
- Psimoulis, P.A.; Stiros, S.C. Measuring deflections of a short-span railway bridge using a robotic total station. J. Bridge Eng. 2013, 18, 182–185. [Google Scholar] [CrossRef]
- Sousa, J.J.; Hlaváčová, I.; Bakoň, M.; Lazecký, M.; Patrício, G.; Guimarães, P.; Bento, R. Potential of multi-temporal InSAR techniques for bridges and dams monitoring. Procedia Technol. 2014, 16, 834–841. [Google Scholar] [CrossRef]
- Caldera, S.; Realini, E.; Barzaghi, R.; Reguzzoni, M.; Sansò, F. Experimental Study on Low-Cost Satellite-Based Geodetic Monitoring over Short Baselines. J. Surv. Eng. 2016, 142, 04015016. [Google Scholar] [CrossRef]
- Sampietro, D.; Caldera, S.; Capponi, M.; Realini, E. Geoguard—An Innovative Technology Based on Low-cost GNSS Receivers to Monitor Surface Deformations. In Proceedings of the First Eage Workshop on Practical Reservoir Monitoring, Amsterdam, The Netherlands, 6–9 March 2017. [Google Scholar]
- Li, H.-N.; Yi, T.-H.; Yi, X.-D.; Wang, G.-X. Measurement and analysis of wind-induced response of tall building based on GPS technology. Adv. Struct. Eng. 2007, 10, 83–93. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- The Forth Bridges. Available online: https://www.theforthbridges.org/forth-road-bridge/facts-and-figures/ (accessed on 17 February 2018).
- Transport Scotland. Available online: https://www.transport.gov.scot/publication/forth-replacement-crossing-environmental-statement/j11223-007/#22 (accessed on 17 February 2018).
- Business Applications. Available online: https://artes-apps.esa.int/projects/showcases/monitoring-bridges-space (accessed on 17 February 2018).
- Rizos, C. Alternatives to current GPS-RTK services and some implications for CORS infrastructure and operations. GPS Solut. 2007, 11, 151–158. [Google Scholar] [CrossRef]
- Geng, J.; Shi, C. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously. J. Geod. 2016, 91, 361–374. [Google Scholar] [CrossRef]
- Gil, H.; Park, J.; Cho, J.; Jung, G. Renovation of structural health monitoring system for Seohae bridge, Seoul, South Korea. Transp. Res. Rec. 2010, 2201, 131–138. [Google Scholar] [CrossRef]
- Ogundipe, O.; Roberts, G.W.; Brown, C.J. GPS monitoring of a steel box girder viaduct. Struct. Infrastruct. Eng. 2014, 10, 25–40. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef]
- Williams, S. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Santamaría Gómez, A.; Bouin, M.N.; Collilieux, X.; Woeppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Langbein, J. Estimating rate uncertainty with maximum likelihood: Differences between power-law and flicker–random-walk models. J. Geod. 2012, 86, 775–783. [Google Scholar] [CrossRef]
- Langbein, J. Noise in GPS displacement measurements from Southern California and Southern Nevada. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- King, M.A.; Williams, S.D. Apparent stability of GPS monumentation from short-baseline time series. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Davis, J.L.; Wernicke, B.P.; Tamisiea, M.E. On seasonal signals in geodetic time series. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Zhou, X. Effect of the span of Australian GPS coordinate time series in establishing an optimal noise model. Sci. China Earth Sci. 2015, 58, 523–539. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R. Noise in multivariate GPS position time-series. J. Geod. 2009, 83, 175–187. [Google Scholar] [CrossRef]
- Wang, J.; Meng, X.; Qin, C.; Yi, J. Vibration Frequencies Extraction of the Forth Road Bridge Using High Sampling GPS Data. Shock Vib. 2016, 2016. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H. Thermal Load in Large-Scale Bridges: A State-of-the-Art Review. Int. J. Distrib. Sens. Netw. 2013, 9. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S.I. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107. [Google Scholar] [CrossRef]
- Hill, E.M.; Davis, J.L.; Elósegui, P.; Wernicke, B.P.; Malikowski, E.; Niemi, N.A. Characterization of site-specific GPS errors using a short-baseline network of braced monuments at Yucca Mountain, southern Nevada. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Yang, L.; Wang, G.; Bao, Y.; Kearns, T.J.; Yu, J. Comparisons of ground-based and building-based CORS: A case study in the region of Puerto Rico and the Virgin Islands. J. Surv. Eng. 2015, 142, 05015006. [Google Scholar] [CrossRef]
- Holický, M.; Marková, J. Thermal Actions. 2008. Available online: http://eurocodes.jrc.ec.europa.eu/doc/WS2008/Holicky_Markova_2008.pdf (accessed on 22 February 2018).
- Roy, R.; Agrawal, D.K.; Mckinstry, H.A. Very Low Thermal Expansion Coefficient Materials. Ann. Rev. Mater. Res. 1989, 19, 59–81. [Google Scholar] [CrossRef]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Wind_chill (accessed on 17 February 2018).













| Component | Linear Velocity (mm/year) | Annual Oscillation | Semi-Annual Oscillation | ||
|---|---|---|---|---|---|
| Amplitude (mm) | Phase (°) | Amplitude (mm) | Phase (°) | ||
| Z | –4.7 ± 0.1 | 9.3 ± 0.1 | 239 ± 1 | 0.7 ± 0.1 | 277 ± 8 |
| Component | Annual Oscillation | Semi-Annual Oscillation | ||
|---|---|---|---|---|
| Amplitude (mm) | Phase (°) | Amplitude (mm) | Phase (°) | |
| GVD | 9.2 ± 1.8 | 268 ± 12 | 5.6 ± 1.8 | 293 ± 18 |
| TED | 9.3 ± 0.6 | 240 ± 4 | 2.1 ± 0.6 | 11 ± 16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Jiang, W.; Meng, X.; Jiang, P.; Wang, K.; Xie, Y.; Ye, J. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sens. 2018, 10, 364. https://doi.org/10.3390/rs10030364
Chen Q, Jiang W, Meng X, Jiang P, Wang K, Xie Y, Ye J. Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sensing. 2018; 10(3):364. https://doi.org/10.3390/rs10030364
Chicago/Turabian StyleChen, Qusen, Weiping Jiang, Xiaolin Meng, Peng Jiang, Kaihua Wang, Yilin Xie, and Jun Ye. 2018. "Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK" Remote Sensing 10, no. 3: 364. https://doi.org/10.3390/rs10030364
APA StyleChen, Q., Jiang, W., Meng, X., Jiang, P., Wang, K., Xie, Y., & Ye, J. (2018). Vertical Deformation Monitoring of the Suspension Bridge Tower Using GNSS: A Case Study of the Forth Road Bridge in the UK. Remote Sensing, 10(3), 364. https://doi.org/10.3390/rs10030364