1. Introduction
Due to the frequent changing of landmarks, especially for rapidly developing cities, it is essential to be able to immediately update such changes for the purposes of navigation and urban planning. Remote-sensing technologies, such as satellite and aerial photography, can capture images of certain areas routinely and serve as useful tools for these types of tasks. In recent years, due to the technical development of imaging sensors and emerging platforms, such as unmanned aerial vehicles, the availability and accessibility of high-resolution remote-sensing imagery have increased dramatically [
1]. Meanwhile, the state-of-the-art deep-learning methods have largely improved the performance of image segmentation. However, more accurate building segmentation results are still critical for further applications such as automatic mapping.
Building detection can be viewed as a specific image segmentation application that segments buildings from their surrounding background. Over the past decades, a great amount of image segmentation algorithms have been proposed. The majority of these algorithms can be classified into four categories: threshold-based, edge-based, region-based and classification-based methods. Image thresholding is a simple and commonly used segmentation method. Pixels with different values are allocated to different parts according to manually or automatically selected thresholds [
2]. Normally, image thresholding is not capable of differentiating among different regions with similar grayscale values. Edge-based methods adopt edge-detection filters, such as Laplacian of Gaussian [
3], Sobel [
4] and Canny [
5], to detect the abrupt changes among neighboring pixels and generate boundaries for segmentation. Region-based methods segment different parts of an image through clustering [
6,
7,
8,
9], region-growing [
10] or shape analysis [
11,
12]. Due to the variety of illuminance and texture conditions of an image, edge-based or region-based methods cannot provide stable and generalized results. Unlike the other three methods, classification-based methods treat image segmentation as a process of classifying the category of every pixel [
13]. Since the segmentation is made by classifying every pixel, the classification-based method can produce more precise segmentations with proper feature extractors and classifiers.
Before deep learning, traditional classification-based methods must undergo a two-step procedure of feature extraction and classification. The spatial and textural features of an image are extracted through mathematical feature descriptors, such as haar-like [
14], scale-invariant feature transform [
15], local binary pattern [
16], and histogram of oriented gradients (HOG) [
17]. After that, the prediction for every pixel is made on the basis of the extracted features through classifiers such as support vector machines [
18], adaptive boosting (AdaBoost) [
19], random forests [
20] and conditional random fields (CRF) [
21]. However, because of the complexity of building structures and also because of strong similarities with other classes (e.g., pieces of roads), the prediction results rely heavily on manual feature design and adaptation, which easily leads to bias and poor generalization.
With the development of algorithms, computational capability and the availability of big data, convolutional neural networks (CNNs) [
22] have attracted more and more attention in this field. Unlike two-step methods requiring artificial feature extraction, CNNs can automatically extract features and make classifications through sequential convolutional and fully connected layers. The CNN method can be considered as a one-step method that combines feature extraction and classification within a single model. Since the feature extraction is learned from the data itself, CNN usually possesses better generalization capability.
In the early stages, patch-based CNN approaches label a pixel by classifying the patch that centers around that pixel [
23,
24]. Even for a small patch of 32 × 32 pixels, to cover the whole area, the memory cost of these patch-based methods increases by 32 × 32 times. For larger areas or patch sizes, these approaches encounter dramatically increased memory cost and significantly reduced processing efficiency [
25]. Fully convolutional networks (FCNs) improve this problem greatly by replacing the fully connected layer with upsampling operations [
26]. Through multiple convolutional and upsampling operations, the FCN model allows efficient pixel-to-pixel classification of an image. However, the FCN model and other similar convolutional encoder–decoder models, such as SegNet [
27] and DeconvNet [
28], use only part of layers to generate the final output, leading to lower edge accuracy.
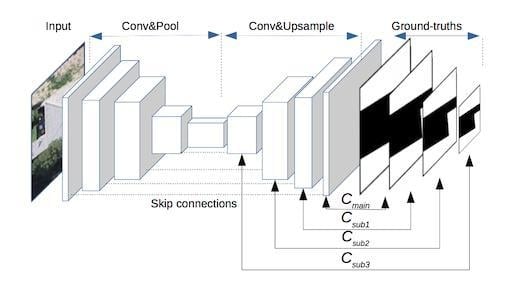
To overcome this limitation, one of the state-of-the-art fully convolutional models, U–Net [
29], adopts bottom-up/top-down architecture with skip connections that combine both the lower and higher layers to generate the final output, resulting in better performance. However, the U–Net model also has its own limitations: (1) At training phase, the parameter updating of both-end layers is prior to those of the intermediate layers (i.e., the layers closer to the top of the feature pyramid) during every backpropagation iteration, which makes the intermediate layers less semantically meaningful [
30]; and (2) the existing study has indicated that multi-scale feature representation (contributed by both end layers and intermediate layers) is very useful for improving the performance and generalization capability of the model [
31], while in the classic U–Net model, due to the loose constraint for the intermediate features, the multi-scale feature representation could be further enhanced if explicit constraints are applied directly on these layers.
Based on the above analysis, we propose a novel architecture of deep fully convolutional networks with multi-constraints, termed multi-constraint fully convolutional networks (MC–FCNs). The MC–FCN model adopts the basic structure of a U–Net and adds multi-scale constraints for variant layers. Here, an optimization target between the prediction and the corresponding ground truth for a certain layer is defined as a constraint. During every iteration, parameters are updated through the multi-constraints, which prevents the parameters from biasing to a single constraint. Also, the constraints are applied on different layers, which helps to better optimize the hidden representation of variant layers. The experiments on a very-high-resolution aerial image dataset with a coverage area of 18 km in New Zealand demonstrate the effectiveness of the proposed MC–FCN model. In comparative trials, the mean values of Jaccard index, overall accuracy and kappa coefficient achieved by our method are 0.833, 0.976 and 0.893, respectively, which are better than those achieved by the classic U–Net model, and significantly outperform the classic FCN and the Adaboost methods using features extracted by HOG. Furthermore, the sensitivity analysis indicates that constraints applied on different layers have impacts of varying degrees on the improvement performance of the proposed model. The main contributions of this study are summarized as follows: (1) We propose a novel multi-constraint fully convolutional architecture that increases the performance of the state-of-the-art method (i.e., U–Net) in building segmentation of very-high-resolution aerial imagery; and (2) we further analyze the effects of different combinations of constraints in MC–FCN to explore how these constraints affect the performance of the deep CNN models.
The remainder of this paper is organized as follows. The materials and methods are described in
Section 2, where the configuration details of the network are also presented. In
Section 3, the results of evaluation and the sensitivity analysis are introduced. The discussion and conclusions are made in
Section 4 and
Section 5, respectively.
3. Results
The classic FCN and U–Net model are adopted as the baseline deep-learning methods for comparison. In addition, as a representative classification method based on manually designed features, the AdaBoost classifier using HOG features (HOG–Ada for short) is also involved in the trials.
3.1. Qualitative Result Comparison
Figure 4 shows that the U–Net and MC–FCN methods are better than FCN, and significantly outperform the HOG–Ada method. In Test-1, HOG–Ada returns more false positives and false negatives than do the other CNN-based methods. However, in the left-middle corner of Test-1, where FCN, U–Net and MC–FCN misclassifies a small lake, HOG–Ada is still able to distinguish the lake with the help of textual features. In regions occupied by non-building backgrounds (Test-3), MC–FCN and U–Net show a significantly smaller number of false positives than other methods, while maintaining high completeness in building extraction. Similar comparison results can be observed from Test-2.
Figure 5 shows the enlarged segmentation results of the center patches from the Test-1, Test-2 and Test-3 regions. In general, the U–Net and MC–FCN methods significantly outperform the FCN and HOG–Ada methods. From rows 2 and 3, although the FCN method outperforms HOG–Ada in detecting buildings (in Test-1 and -2), it sometimes performs even worse in background recognition (in Test-3). From rows 4 and 5, especially in Test-1, MC–FCN returns a similar number of true positives but much fewer false positives than does U–Net for variant types of landmarks. The visual observation is consistent with quantitative comparison results of
Table 5, which indicates that the MC–FCN model shows higher increments of precision rather than those of recall.
Since there is a large number of building samples in our experiment, in order to generate an objective reflection of the segmentation results, several samples are randomly selected for comparison first.
Figure 6 presents the results of the samples from the Test-1, Test-2 and Test-3 regions generated by the HOG–Ada, FCN, U–Net and MC–FCN methods. In row 2, the HOG–Ada method is not able to extract buildings in most cases (in a, b, d, e and h). In c, f and g, although the HOG–Ada method correctly extracts major parts of the buildings, it still returns a significant number of false positives. In row 3, the FCN method shows quite good building extraction but still sometimes produces obvious false positives in the backgrounds (in a, f, g and h). From rows 4 and 5, the MC–FCN and U–Net methods present better performance in building extraction and noise reduction. When comparing the two, detectable improvements of MC–FCN over U–Net can be observed in restoring building boundaries (a, b, e, f and h) and suppressing false positives (a, e and h).
In order to further explore the improvements of our method over the classic U–Net, some representative samples were selected for additional comparison.
Figure 7 shows the results of eight buildings generated by the U–Net and MC–FCN methods. The results indicate that both MC–FCN and U–Net methods are able to accurately extract the major parts of the buildings. Compared with the U–Net method, the MC–FCN method shows considerably fewer false positives, especially around the building edges (a, b, d, e and g) or in the gap areas between buildings (c, f and h). Interestingly, in some cases, the MC–FCN method also has better performance within the building boundaries (b and c).
3.2. Quantitative Result Comparison
Five commonly used metrics for image segmentation, including precision, recall, Jaccard index, overall accuracy and kappa coefficient, are used for quantitative evaluation in this study.
Table 5 shows the comparison results of the four different methods for Test-1, Test-2 and Test-3 regions.
In the case of precision, the MC–FCN method holds the highest values among all testing regions, which indicates that our method performs well in suppressing false positives. Compared with U–Net, MC–FCN achieves 3.0% relative increase (0.890 vs. 0.864) on the mean value of precision. Particularly, in the test region with less residential area (Test-3), we achieve more significant improvement by gaining 4.4% relative increment of precision (0.862 vs. 0.826) over U–Net.
As for recall, the MC–FCN method presents the highest values of this value in Test-1 and Test-2 regions. Surprisingly, the FCN method outperforms the U–Net and MC–FCN methods in Test-3. Nonetheless, this slight advantage for FCN is far from being significant due to its low performance in other evaluation metrics. The difference between MC–FCN and U–Net in recall is not evident, although the former is slightly better than the latter in all three test regions.
For the Jaccard index, all methods except for HOG–Ada achieve their highest values in Test-2. Within all testing regions, the values of the Jaccard index from the MC–FCN method are the highest. The increments of MC–FCN over U–Net are more significant in regions with more complicated backgrounds (Test-1 and Test-3 regions). The increments of the Test-1, Test-2 and Test-3 regions are 0.026, 0.019 and 0.032, respectively. MC–FCN improves on the mean value of the Jaccard index of U–Net from 0.807 to 0.833 with a relative increase of about 3.2%.
As for overall accuracy, four methods obtain their highest values in the Test-3 region. Since overall accuracy only focuses on the correctness of pixel classification, even the smallest mean overall accuracy of the four methods reached 0.844 (HOG–Ada). The results of the MC–FCN method are the best among all regions.
As with the kappa coefficient, the four methods, except for the HOG–Ada, reached their highest values of the kappa coefficient in the Test-2 region. MC–FCN shows the highest kappa values across the Test-1, Test-2 and Test-3 regions. Compared with HOG–Ada, FCN and U–Net, the mean values of this metric increase were 0.453, 0.290 and 0.019, respectively.
3.3. Sensitivity Analysis of Constraints
The sensitivity to the number of applied subconstraints is analyzed.
Figure 8 presents the representative segmentation results from MC–FCN models with 0, 1, 2 or 3 subconstraints. Looking from top to bottom, MC–FCN models with more subconstraints result in slightly fewer false positives (a, d, f and h). However, in some cases, more subconstraints lead to more false negatives and weaker performance (b and g).
In
Table 6, the evaluation results of the MC–FCN models with 0, 1, 2 and 3 subconstraints are listed. The values of Jaccard index, overall accuracy or kappa coefficient indicate that having more constraints generally increases the performance of the MC–FCN, although models with two or three subconstraints hold consistent mean values of the three metrics. However, as for the imbalanced metrics, precision and recall show an inconsistent trend of increments, which implies that the model becomes unstable in controlling false predictions when the number of subconstraints increases.
Figure 9 shows the representative segmentation results from MC–FCN models with constraint combinations of
only,
,
or
. The MC–FCN models with constraint combinations of
and
have much fewer false positive, especially at building edges (a, b, e, g and h) or in the gaps between buildings (c).
Table 7 shows the evaluation results of the MC–FCN models with constraint combinations of
only,
,
or
. It turns out that the performance of the model with the constraint combination of
is better than those of other combinations. Apparently, the better performance of this combination benefits from a good tradeoff between precision and recall.
3.4. Computational Efficiency
Considering the relatively closer performance, an efficiency comparison between different deep-learning methods was conducted. The algorithms of FCN, U–Net and MC–FCN were implemented in Keras using Tensorflow as backend and performed on a 64-bit Ubuntu system (ASUS: Beitou District, Taipei, Taiwan) equipped with NVIDIA GeForce GTX 1070 GPU (Nvidia: Santa Clara (HQ), CA, USA) graphic device with 8G byte graphic memory. During training, the Adam stochastic optimizer [
42] with a learning rate of 0.001 was used. The difference of computational efficiency between these methods mainly lies in the time cost of the training process, which is generally proportional to the complexity of the model. The FCN, U–Net and the proposed MC–FCN models require 178.3, 365.7 and 372.1 min, respectively, for 100 epochs of iterations using the same training dataset. It can be concluded that MC–FCN gains 3.0% (0.833 vs. 0.807) and 2.2% (0.893 vs. 0.874) relative increments of Jaccard index and kappa coefficient, respectively, over U–Net with the cost of only 1.8% increment of model-training time; the extra time brings a cost-effective improvement of the segmentation performance.
4. Discussions
4.1. About the Proposed MC–FCN Model
The proposed MC–FCN model follows the basic structure of U–Net [
29]. From the perspective of model design, our major improvement is applying a 1 × 1 convolution operation for the intermediate layers of the top-down feature pyramid to generate additional predictions, which enables multi-constraints on different spatial scales for the model during the training process. Although the effectiveness of multi-constraints applied on FCNs has been demonstrated by Xie et al. [
30], their work was conducted based on the FCN framework for application of edge detection. However, in our study, targeting building segmentation from aerial images, the more effective U–Net architecture is adopted. Another related study has proven the usefulness of multi-scale prediction based on the feature pyramid [
31]. However, compared with our approach, their study focused more on fusing the features extracted from different scales to achieve higher performance, and the multi-constraints were not explicitly applied on the intermediate layers in their model.
In the field of remote sensing, some studies on the detection of informal settlements [
43] or buildings in rural areas [
24,
44] have demonstrated the potential of applying CNN architectures for high-accuracy automatic building detection. However, their patch-based CNN methods usually require large amounts of memory and computational capability, which limit the applicability of these methods to large areas. There are also other studies [
45,
46] that segment aerial imagery in an end-to-end fully convolutional manner, and these approaches significantly reduce the usage of memory and improve segmentation accuracy. However, their methods are built up by the classic FCN model, which simply upsamples intermediate layers (no skip connection) and leads to insufficient precision. The state-of-the-art U–Net model that we use for building segmentation shows better performance. More recently, by integrating the architecture of U–Net and the deep residual networks (ResNet) [
47], Xu et al. achieved high performance in accurately extracting buildings from aerial imagery [
48]. However, compared with our approach, they adopted infrared band data and the digital surface model besides RGB images to improve the accuracy. Meanwhile, multi-constraints applied on intermediate layers, which are proven effective in our MC–FCN model, were not considered in Xu et al.’s work.
4.2. Accuracies, Uncertainties and Limitations
As compared to the AdaBoost methods using hand-crafted feature descriptors (HOG–Ada), classic fully convolutional networks (FCNs) and the state-of-the-art fully convolutional model (U–Net), our MC–FCN model showed better performance in the evaluation metrics of the Jaccard index, overall accuracy and kappa coefficient. Particularly, the mean values of the kappa coefficient of the MC–FCN, U–Net, FCN and HOG–Ada methods are 0.893, 0.874, 0.603 and 0.440, respectively. Our MC–FCN method is better than the U–Net and FCN methods, and significantly outperforms the HOG–Ada method.
In the sensitivity analysis of the MC–FCN, when gradually increasing the number of subconstraints in ascending order, models with more subconstraints () performed better. Also, when applying only one subconstraint along with the main constraint, different combinations led to different impacts on the performance. Specifically, the farther the – combination, the better the model performs. Another interesting finding is that the model with two constraints outperforms that with all four constraints. The increments of the Jaccard index and the kappa coefficient by the MC–FCN model with and reach 0.026 and 0.019, respectively, whereas these numbers are 0.015 and 0.012, respectively, in the case of the MC–FCN model with and . This demonstrates that the improvement of the performance is affected more by the positions of the subconstraints rather than the number of them.
Previous applications of ResNet have shown that a deeper network is very likely to lead to better results. However, the effectiveness of applying multi-constraints on a deeper network remains uncertain for us. The model scales are determined by two important factors: the scale of data as well as the computational capability. Although a deeper neural network has greater representation capability, it is better to have a large-enough dataset for training in order to avoid overfitting. In our study, the overfitting problem is well handled when applying a relatively deep network. Meanwhile, the computational capability should also be considered because of efficiency requirements in the experiment. In this approach, when high accuracy was achieved, we fixed the number of layers due to limited computing resources.
In general, CNN-based methods, especially our proposed MC–FCN method, significantly outperform the HOG–Ada method in building extraction and background elimination. However, in the left-middle corner of Test-1 (see
Figure 10), the CNN-based methods have a number of misclassified pixels, while the HOG–Ada method produces quite clean results with simple RGB and texture features extracted by the HOG descriptor. The ability to adaptively adjust the parameters by the feeding data is an advantage for the CNN method but can also sometimes be a limitation when there are insufficient training data. Recent research [
49,
50], which combines hand-crafted features and CNN-learned features, shows promising improvement. As a continuation of this work, additional data sources (e.g., more complicated background types), as well as the fusion of hand-crafted features and CNN-learned features, could be considered for improving this limitation.