Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans
Abstract
:1. Introduction
1.1. Description of the Baltic Sea
1.2. Theory of Inherent Optical Properties
1.3. Atmospheric Correction Models
1.4. Forward Modelling
1.5. Retrieval of Level 2 Products via Inverse Modelling
2. Materials and Methods
2.1. Baltic Data Set
2.2. Reference Data Set
2.3. Optical Measurements in the Baltic Sea
2.4. AC9 and TACCS Data Processing
2.5. Spectral Slope of Particle Scattering
2.6. Volume Scattering Function (VSF) Measurements and Calibration
2.7. Water Samples and Data Analysis
2.7.1. CDOM Measurements
2.7.2. Suspended Particulate Matter
2.7.3. Chlorophyll Analysis
2.7.4. Non-Algal Particle Absorption
2.7.5. Chlorophyll-Specific Absorption and Absorption of Non-Algal Particles (NAP)
2.7.6. aNAP Slope Calculations
3. Results
3.1. Ranges of Optical Parameters in the Baltic Sea
3.2. Chlorophyll-Specific Absorption Derived from the Filter-Pad Method
3.3. Absorption of Non-Algal Particles
3.4. Spectral Slope of NAP and CDOM Absorption
3.5. Particle Scatter and Backscatter
3.6. Backscatter Ratio and Phase Function
3.7. Implications for Algorithms
4. Discussion
4.1. Chlorophyll-a Specific Absorption
4.2. Particle Absorption and Scatter
4.3. The Phase Function in the Baltic Sea
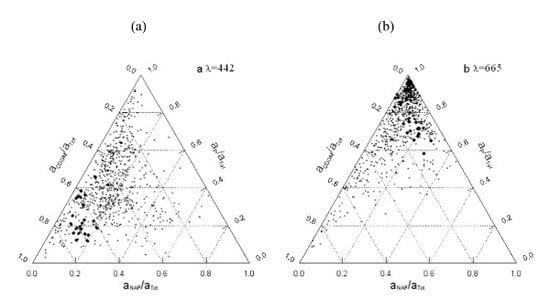
4.4. Ternary Plots and Implications for Algorithms
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| Abbreviation | Optical Property | Unit |
| ℜ | Air water interface term | dimensionless |
| ρw | Above water reflectance | dimensionless |
| Particulate backscattering ratio | dimensionless | |
| Relative refractive index of particles | dimensionless | |
| Normalized phase function | sr−1 | |
| The spectral slope of scattering | dimensionless | |
| The spectral slope of backscattering | dimensionless | |
| aCDOM(440) | CDOM absorption at 440 nm | m−1 |
| ad [SPM]* | SPM specific absorption | m2 g−1 |
| aNAP | Non Algal Particle absorption coefficient | m−1 |
| ap | phytoplankton absorption coefficient | m−1 |
| ap* | phytoplankton specific absorption coefficient | m2 mg−1 |
| atot | Total absorption coefficient | m−1 |
| aw | Water absorption coefficient | m−1 |
| b*p [SPM] | SPM specific scattering coefficient | m2 g−1 |
| bb*p [SPM] | SPM specific backscattering coefficient | m2 g−1 |
| bbp | Particulate backscattering coefficient | m−1 |
| bbtot | Total backscattering coefficient | m−1 |
| bbw | Water scattering coefficient | m−1 |
| btot | Total scattering coefficient | m−1 |
| f | Empirical factor relating IOPs to R | dimensionless |
| F | Empirical factor relating IOPs to ρw | dimensionless |
| f’ | Empirical factor relating IOPs to R | dimensionless |
| F’ | Empirical factor relating IOPs to ρw | dimensionless |
| nw | Refractive index of seawater | dimensionless |
| OD(λ) | Optical Density | dimensionless |
| Q | Ratio of upwelling irradiance to radiance | dimensionless |
| r | Air-water reflectance for diffuse irradiance | dimensionless |
| SCDOM | The spectral slope of CDOM absorption | dimensionless |
| SNAP | The spectral slope of NAP absorption | dimensionless |
| λ | Wavelength | nm |
| Junge slope | dimensionless | |
| ρw | Water reflectance (above surface) | dimensionless |
References
- Voipio, A. The Baltic Sea; Elsevier: Amsterdam, The Netherlands, 1981; Volume 30, p. 417. ISBN 9780080870687. [Google Scholar]
- Snoeijs-Leijonmalm, P.; Andrén, E. Why is the Baltic Sea so special to live in? In Biological Oceanography of the Baltic Sea; Snoeijs-Leijonmalm, P., Schubert, H., Radziejewska, T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 23–84. ISBN 978-94-007-0668-2. [Google Scholar]
- Kowalczuk, P.; Stedmon, C.A.; Markager, S. Modelling absorption by CDOM in the Baltic Sea from season, salinity and chlorophyll. Mar. Chem. 2006, 101, 1–11. [Google Scholar] [CrossRef]
- Kratzer, S.; Tett, P. Using bio-optics to investigate the extent of coastal waters: A Swedish case study. Hydrobiologia 2009, 629, 169–186. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: New York, NY, USA, 1984; p. 649. ISBN 978-0-521-15175-7. [Google Scholar]
- Højerslev, N.K.; Holt, N.; Aarup, T. Optical measurements in the North Sea-Baltic Sea transition zone. I. On the origin of the deep water in the Kattegat. Cont. Shelf Res. 1996, 16, 1329–1342. [Google Scholar] [CrossRef]
- Harvey, E.T.; Kratzer, S.; Andersson, A. Relationships between colored dissolved organic matter and dissolved organic carbon in different coastal gradients of the Baltic Sea. AMBIO 2015, 44, 392–401. [Google Scholar] [CrossRef] [PubMed]
- Harvey, T. Bio-Optics, Satellite Remote Sensing and Baltic Sea Ecosystems: Applications for Monitoring and Management. Ph.D. Thesis, Department of Ecology, Environment and Plant Sciences, Stockholm University, Stockholm, Sweden, 2015. [Google Scholar]
- Ohde, T.; Siegel, H.; Gerth, M. Validation of MERIS Level-2 products in the Baltic Sea, the Namibian coastal area and the Atlantic Ocean. Int. J. Remote Sens. 2007, 28, 609–624. [Google Scholar] [CrossRef]
- Fleming-Lehtinen, V.; Laamanen, M. Long-term changes in Secchi depth and the role of phytoplankton in explaining light attenuation in the Baltic Sea. Estuar. Coast. Shelf Sci. 2012, 102, 1–10. [Google Scholar] [CrossRef]
- Kowalczuk, P.; Olszewski, J.; Darecki, M.; Kaczmarek, S. Empirical relationships between Coloured Dissolved Organic Matter (CDOM) absorption and apparent optical properties in Baltic Sea waters. Int. J. Remote Sens. 2005, 26, 345–370. [Google Scholar] [CrossRef]
- Wasmund, N.; Andrushaitis, A.; Łysiak-Pastuszak, E.; Müller-Karulis, B.; Nausch, G.; Neumann, T.; Ojaveer, H.; Olenina, I.; Postel, L.; Witek, Z. Trophic status of the South-Eastern Baltic Sea: A comparison of coastal and open areas. Estuar. Coast. Shelf Sci. 2001, 53, 849–864. [Google Scholar] [CrossRef]
- Woźniak, S.B.; Meler, J.; Lednicka, B.; Zdun, A.; Stoń-Egiert, J. Inherent optical properties of suspended particulate matter in the southern Baltic Sea. Oceanologia 2011, 53, 691–729. [Google Scholar] [CrossRef]
- Vaičiūtė, D.; Bresciani, M.; Bučas, M. Validation of MERIS bio-optical products with in situ data in the turbid Lithuanian Baltic Sea coastal waters. J. Appl. Remote Sens. 2012, 6, 063568. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S.; Reinart, A.; Kauer, T.; Paavel, B. Robust remote sensing algorithms to derive the diffuse attenuation coefficient for lakes and coastal waters. Limnol. Oceanogr. Methods 2015, 13, 402–415. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S.; Reinart, A. Robust Kd(490) and Secchi algorithms for remote sensing of optically complex waters. In Proceedings of the Ocean Optics XXI Conference, Glasgow, UK, 8–12 October 2012. [Google Scholar]
- Raag, L.; Sipelgas, L.; Uiboupin, R. Analysis of natural background and dredging-induced changes in TSM concentration from MERIS images near commercial harbours in the Estonian coastal sea. Int. J. Remote Sens. 2014, 35, 6764–6780. [Google Scholar] [CrossRef]
- Toming, K.; Arst, H.; Paavel, B.; Laas, A.; Nõges, T. Spatial and temporal variations in coloured dissolved organic matter in large and shallow Estonian water bodies. Boreal Environ. Res. 2009, 14, 959–970. [Google Scholar]
- Vazyulya, S.; Khrapko, A.; Kopelevich, O.; Burenkov, V.; Eremina, T.; Isaev, A. Regional algorithms for the estimation of chlorophyll and suspended matter concentration in the Gulf of Finland from MODIS-Aqua satellite data. Oceanologia 2014, 56, 737–756. [Google Scholar] [CrossRef]
- Koponen, S.; Attila, J.; Pulliainen, J.; Kallio, K.; Pyhälahti, T.; Lindfors, A.; Rasmus, K.; Hallikainen, M. A case study of airborne and satellite remote sensing of a spring bloom event in the Gulf of Finland. Cont. Shelf Res. 2007, 27, 228–244. [Google Scholar] [CrossRef]
- Suikkanen, S.; Laamanen, M.; Huttunen, M. Long-term changes in summer phytoplankton communities of the open northern Baltic Sea. Estuar. Coast. Shelf Sci. 2007, 71, 580–592. [Google Scholar] [CrossRef]
- Fleming-Lehtinen, V.; Laamanen, M.; Kuosa, H.; Haahti, H.; Olsonen, R. Long-term development of inorganic nutrients and chlorophyll α in the open northern Baltic Sea. AMBIO 2008, 37, 86–92. [Google Scholar] [CrossRef]
- Walsby, A.E.; Hayes, P.K.; Boje, R. The gas vesicles, buoyancy and vertical distribution of cyanobacteria in the Baltic Sea. Eur. J. Phycol. 1995, 30, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, E.J.; Capone, D.G. Marine Pelagic Cyanobacteria: Trichodesmium and Other Diazotrophs; Springer Science and Business Media: Berlin, Germany, 2013; Volume 362, ISBN 978-94-015-7977-3. [Google Scholar]
- Kahru, M.; Leppanen, J.M.; Rud, O. Cyanobacterial blooms cause heating of the sea surface. Mar. Ecol. Prog. Ser. 1993, 101, 1–7. [Google Scholar] [CrossRef]
- Subramaniam, A.; Kratzer, S.; Carpenter, J.C.; Söderbäck, E. Remote sensing and optical in-water measurements of a cyanobacteria bloom in the Baltic Sea. Best of plenary session. In Proceedings of the Sixth International Conference on Remote Sensing for Marine and Coastal Environments, Charleston, SC, USA, 1–3 May 2000. [Google Scholar]
- Jerlov, N. Marine Optics. In Elsevier Oceanography Series 14; Elsevier: New York, NY, USA, 1976; p. 231. [Google Scholar]
- Bukata, R.P.; Jerome, J.H.; Kondratyev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995; ISBN 9780849347542. [Google Scholar]
- Bowers, D.G.; Binding, C.E. The Optical Properties of Mineral Suspended Particles: A Review and Synthesis. Estuar. Coast. Shelf Sci. 2006, 67, 219–230. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Jerome, J.H.; Bukata, R.P.; Letourneau, G. An assessment of MERIS algal products during an intense bloom in Lake of the Woods. J. Plankton Res. 2010, 33, 793–806. [Google Scholar] [CrossRef]
- Kuhrts, C.; Fennel, W.; Seifert, T. Model studies of transport of sedimentary material in the western Baltic. J. Mar. Syst. 2004, 52, 167–190. [Google Scholar] [CrossRef]
- Preisendorfer, R.W. Application of Radiative Transfer theory to Light Measurements in the Sea. In Proceedings of the Symposium on Radiant Energy in the Sea, International Union of Geodetic and Geophysics, Helsinki, Finland, 4–5 August 1960. [Google Scholar]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters: Its dependence on sun angle as influenced by the molecular scattering contribution. Appl. Opt. 1991, 30, 4427–4438. [Google Scholar] [CrossRef] [PubMed]
- Petzold, T.J. Volume Scattering Functions for Selected Natural Waters; No. SIO-REF-72-78; Scripps Institution of Oceanography La Jolla Ca Visibility Laboratory: San Diego, CA, USA, 1972; p. 77. [Google Scholar]
- Wang, M. Atmospheric correction for remotely-sensed ocean-colour products. In Reports and Monographs of the International Ocean-Colour Coordinating Group (IOCCG); IOCCG: Dartmouth, Canada, 2010; Available online: www.vliz.be/imisdocs/publications/ocrd/259206.pdf (accessed on 6 March 2018).
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Moore, G.F.; Aiken, J.; Lavender, S.J. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: Application to MERIS. Int. J. Remote Sens. 1999, 20, 1713–1733. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll-a concentration in case II waters using MODIS and MERIS data—Successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef]
- Goyens, C.; Jamet, C.; Schroeder, T. Evaluation of four atmospheric correction algorithms for MODIS-Aqua images over contrasted coastal waters. Remote Sens. Environ. 2013, 131, 63–75. [Google Scholar] [CrossRef]
- Mobley, C.D. Hydrolight 3.0 Users Guide; SRIRI Project 5632; SRI International: Menlo Park, CA, USA, 1995; p. 65. [Google Scholar]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef] [PubMed]
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Hoepffner, N.; Sathyendranath, S. Bio-optical characteristics of coastal waters: Absorption spectra of phytoplankton and pigment distribution in the western North Atlantic. Limnol. Oceanogr. 1992, 37, 1660–1679. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. Oceans 1995, 100, 13321–13332. [Google Scholar] [CrossRef]
- Kratzer, S. Bio-Optical Studies of Coastal Waters. Ph.D. Thesis, School of Ocean Sciences, University of Wales, Bangor, UK, 2000. [Google Scholar]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data (300 m spatial resolution) to monitor coastal waters—A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Kratzer, S.; Vinterhav, C. Improvement of MERIS level 2 products in baltic sea coastal areas by applying the improved Contrast between Ocean and Land Processor (ICOL)—Data analysis and validation. Oceanologia 2010, 52, 211–236. [Google Scholar] [CrossRef]
- Beltrán-Abaunza, J.M.; Kratzer, S.; Brockmann, C. Evaluation of MERIS products from Baltic Sea coastal waters rich in CDOM. Ocean Sci. 2014, 10, 377–396. [Google Scholar] [CrossRef]
- Doerffer, R. Protocols for the Validation of MERIS Water Products; European Space Agency Doc. No. PO-TN-MEL-GS-0043; GKSS: Geesthacht, Germany, 2002; pp. 1–42. [Google Scholar]
- Schroeder, T.; Behnert, I.; Schaale, M.; Fischer, J. Retrieval of atmospheric and oceanic properties from MERIS measurements: A new Case-2 water processor for BEAM. Int. J. Remote Sens. 2007, 28, 5627–5632. [Google Scholar] [CrossRef]
- Craig, S.E.; Jones, C.T.; Li, W.K.W.; Lazin, G.; Horne, E.; Caverhill, C. Deriving optical metrics of coastal phytoplankton biomass from ocean colour. Remote Sens. Environ. 2012, 119, 72–83. [Google Scholar] [CrossRef]
- Woźniak, M.; Craig, S.; Kratzer, S.; Wojtasiewicz, B.; Darecki, M. A Novel Statistical Approach for Ocean Colour Estimation of Inherent Optical Properties and Cyanobacteria Abundance in Optically Complex Waters. Remote Sens. 2017, 9, 343. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- ESA, Reference Model for MERIS Level 2 Processing, 3rd MERIS Reprocessing. Ocean Branch Issue 5, Rev. 4. Available online: https://earth.esa.int/documents/10174/1462454/Envisat_MERIS_RMD_Third-Reprocessing_Level-2/ (accessed on 21 February 2018).
- ESA ESOV Software Tool. Available online: https://earth.esa.int/web/guest/software-tools/-/article/esov-software-tools-esov-ng-and-esov-classic-1652 (accessed on 21 February 2018).
- Askö Laboratory, Baltic Sea Centre. Available online: http://www.su.se/ostersjocentrum/english/askö-laboratory (accessed on 21 February 2018).
- Baltic Sea Watch System (BAWS), Swedish Meteorological and Hydrological Institute (SMHI). Available online: https://www.smhi.se/klimatdata/oceanografi/algsituationen (accessed on 21 February 2018).
- The Baltic Sea Remote Sensing. The Science of Ocean Colour, a film by Roland Doerffer. Available online: http://www.spicosa.eu/setnet/downloads/ (accessed on 21 February 2018).
- Blender Open Source 3D Creation. Available online: http://www.blender.org (accessed on 21 February 2018).
- NOMAD: NASA Bio-Optical Marine Algorithm Dataset. Available online: https://seabass.gsfc.nasa.gov/wiki/NOMAD (accessed on 21 February 2018).
- Werdell, P.; Bailey, S. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Data Base if the EU MAST Project (MAS3-CT97-0087) COLORS: Coastal Region Long-Term Measurements for Colour Remote Sensing Development and Validation. Available online: http://databases.eucc-d.de/plugins/projectsdb/project.php?show=234 (accessed on 21 February 2018).
- WetLabs AC9/ACS Protocol Documents. Available online: ftp://misclab.umeoce.maine.edu/classes/OO2017/labs_resources/lab2/acprotq_ac9_protocol.pdf (accessed on 21 February 2018).
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65- to 2.5-µm spectral range. Appl. Optics 1993, 32, 3531–3540. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Optical properties of pure water and pure sea water. In Optical Aspects of Oceanography; Jerlov, N.G., Steemann-Nielsen, E., Eds.; Academic: New York, NY, USA, 1974; pp. 1–24. [Google Scholar]
- Pegau, W.S.; Zaneveld, J.R.V. Temperature dependent absorption of water in the red and near infrared portions of the spectrum. Limnol. Oceanogr. 1993, 38, 188–192. [Google Scholar]
- Pegau, W.S.; Gray, D.; Zaneveld, J.R.V. Absorption and attenuation of visible and near-infrared light in water: The dependence on temperature and salinity. Appl. Opt. 1997, 36, 6035–6046. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, J.M.; Twardowski, M.S.; Zaneveld, J.R.V.; Moore, C.M.; Barnard, A.H.; Donaghay, P.L.; Rhoades, B. The hyperspectral temperature and salt dependencies of absorption by water and heavy water in the 400–750 nm spectral range. Appl. Opt. 2006, 45, 5294–5309. [Google Scholar] [CrossRef] [PubMed]
- Kirk, J.T.O. Monte Carlo modeling of the performance of a reflective tube absorption meter. Appl. Opt. 1992, 31, 6463–6468. [Google Scholar] [CrossRef] [PubMed]
- Zibordi, G.; Ruddick, K.; Ansko, I.; Moore, G.; Kratzer, S.; Icely, J.; Reinart, A. In situ determination of the remote sensing reflectance: An inter-comparison. Ocean Sci. 2012, 8, 567–586. [Google Scholar] [CrossRef]
- Lee, M.E.; Lewis, M.R. A New Method for the Measurement of the Optical Volume Scattering Function in the Upper Ocean. J. Atmos. Ocean Tech. 2003, 20, 563–571. [Google Scholar] [CrossRef]
- Strickland, J.H.D.; Parsons, T.R. A Practical Handbook of Sea-Water Analysis. Fisheries Research Board of Canada Bulletin 167, 2nd ed.; Fisheries Research Board of Canada: Ottawa, ON, Canada, 1972. [Google Scholar]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equation for determining chlorophyll a, b, c1 and c2. Biochem. Physiol. Pflanzen 1975, 167, 194–204. [Google Scholar] [CrossRef]
- Parsons, T.R.; Maita, Y.; Lalli, C.M. A Manual of Chemical and Biological Methods for Seawater Analysis, 1st ed.; Pergamon Press: Oxford, UK, 1984; p. 173. ISBN 978-0-08-030287-4. [Google Scholar]
- Jeffrey, S.W.; Welschmeyer, N.A. Appendix F: Spectrophotometric and fluorometric equations in common use in oceanography. In Phytoplankton Pigments in Oceanography. Monographs on Oceanographic Methodology; Jeffrey, S.W., Mantoura, R.F.C., Wright, S.W., Eds.; UNESCO Publishing: Paris, France, 1997; pp. 597–615. ISBN 92-3-103275-5. [Google Scholar]
- Sørensen, K.; Grung, M.; Röttgers, R. An intercomparison of in vitro chlorophyll a determinations for MERIS level 2 data validation. Int. J. Remote Sens. 2007, 28, 537–554. [Google Scholar] [CrossRef]
- Yentsch, C.S. A non-extractive method for the quantitative estimation of chlorophyll in algal cultures. Nature 1957, 179, 1302–1304. [Google Scholar] [CrossRef]
- Kishino, M.; Takahashi, M.; Okami, N.; Ichimura, S. Estimation of the spectral absorption coefficients of phytoplankton in the sea. Bull. Mar. Sci. 1985, 37, 634–642. [Google Scholar]
- Cleveland, J.S.; Weidemann, A.D. Quantifying absorption by aquatic particles: A multiple scattering correction for glass-fiber filters. Limnol. Oceanogr. 1993, 38, 1321–1327. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Boss, E. Phase function effects on oceanic light fields. Appl. Opt. 2002, 41, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Twardowski, M.S.; Boss, E.; Macdonald, J.B.; Pegau, W.S.; Barnard, A.H.; Zaneveld, J.R.V. A model for estimating bulk refractive index from the optical backscattering ratio and the implications for understanding particle composition in case I and case II waters. J. Geophys. Res. Oceans 2001, 106, 14129–14142. [Google Scholar] [CrossRef]
- Gilerson, A.A.; Moses, W.; Ahmed, S.A.; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Ioannou, I. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar] [CrossRef] [PubMed]
- Kahru, M.; Kudela, R.M.; Anderson, C.R.; Manzano-Sarabia, M.; Mitchell, B.G. Evaluation of satellite retrievals of ocean chlorophyll-a in the California current. Remote Sens. 2014, 6, 8524–8540. [Google Scholar] [CrossRef]
- Berthon, J.F.; Zibordi, G. Optically black waters in the northern Baltic Sea. Geophys. Res. Lett. 2010, 37, L09605. [Google Scholar] [CrossRef]
- Gross, L.; Thiria, S.; Frouin, R.; Mitchell, B.G. Artificial neural networks for modeling the transfer function between marine reflectance and phytoplankton pigment concentration. J. Geophys. Res. Oceans 2000, 105, 3483–3495. [Google Scholar] [CrossRef]
- Reinart, A.; Kutser, T. Comparison of different satellite sensors in detecting cyanobacterial bloom events in the Baltic Sea. Remote Sens. Environ. 2006, 102, 74–85. [Google Scholar] [CrossRef]
- Schwarz, J.N.; Kowalczuk, P.; Kaczmarek, S.; Cota, G.F.; Mitchell, B.G.; Kahru, M.; Chavez, F.P.; Cunningham, A.; McKee, D.; Gege, P.; et al. Two models for absorption by coloured dissolved organic matter (CDOM). Oceanologia 2002, 44, 209–241. [Google Scholar]
- Babin, M.; Stramski, D.; Ferrari, G.M.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. Oceans 2003, 108, 3211. [Google Scholar] [CrossRef]
- Roy, S.; Sathyendranath, S.; Bouman, H.; Platt, T. The global distribution of phytoplankton size spectrum and size classes from their light-absorption spectra derived from satellite data. Remote Sens. Environ. 2013, 139, 185–197. [Google Scholar] [CrossRef]
- Simis, S.G.H.; Ylöstalo, P.; Kallio, K.Y.; Spilling, K.; Kutser, T. Contrasting seasonality in optical-biogeochemical properties of the Baltic Sea. PLoS ONE 2017, 12, e0173357. [Google Scholar] [CrossRef] [PubMed]
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light scattering properties of marine particles in coastal and open ocean waters as related to the particle mass concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef]
- Siegel, H.; Gerth, M.; Ohde, T.; Heene, T. Ocean colour remote sensing relevant water constituents and optical properties of the Baltic Sea. Int. J. Remote Sens. 2005, 26, 315–330. [Google Scholar] [CrossRef]
- Freda, W.; Piskozub, J. Improved method of Fournier-Forand marine phase function parameterization. Opt. Express 2007, 15, 12763–12768. [Google Scholar] [CrossRef] [PubMed]
- BEAM ESA Earth Observation and Science Tool. Available online: http://www.brockmann-consult.de/beam/ (accessed on 19 December 2017).
- SNAP ESA Earth Observations and Science Tools. Available online: http://step.esa.int/main/toolboxes/snap/ (accessed on 19 December 2017).













| Baltic Sea Area | [Chl a] | [SPM] | aCDOM | SD | References |
|---|---|---|---|---|---|
| µg L−1 | g m−3 | m−1 | m | ||
| Arkona Sea | 0.3–7.0 | 0.7–9.0 | 0.2–0.4 | 5.0–9.5 | [9,10] |
| Bornholm Sea | 0.4–4.0 | 0.4–5.0 | 0.2–0.3 | 2.0–10.5 | [9] |
| Gotland Sea | 0.2–4.0 | 3.0–6.0 | 0.2–0.4 | 3.0–10.0 | [9] |
| Pomeranian Bight, Germany | 0.4–13.0 | 0.5–20.0 | 0.2–0.9 | 3.0–7.0 | [9,11,12] |
| Gulf of Gdansk Poland | 0.4–72.6 | 0.4–15.7 | 0.4–4.4 | 4.5–7.0 | [11,12,13] |
| SE Baltic Sea, Lithuanian coast | 0.6–116.2 | 1.1–32.0 | 0.01–2.0 | 4.0–6.0 | [12,14] |
| Pärnu Bay, Estonia | 0.7–10.7 | 5.0–24.3 | 0.6–3.7 | 0.5–4.3 | [15,16] |
| Gulf of Riga, Estonia | 2.0–46.0 | 10.0–24.0 | 1.5–13.0 | 3.1–6.9 | [10,17,18] |
| Gulf of Finland | 1.2–130 | 0.8–20.0 | 0.6–1.2 | 1.8–4.0 | [19,20] |
| NW Baltic proper | 0.4–52.4 | 0.5–21.7 | 0.3–4.1 | 0.7–12.8 | [4,8] |
| Öre Estuary, Bothnian Sea, SE | 0.5–96.4 | 0.2–20.9 | 0.75–8.8 | 0.5–6.0 | [8] |
| Data Set | Optical Property | Unit | Range | Median | LQ | UQ | n |
|---|---|---|---|---|---|---|---|
| Baltic Sea | [Chl a] | µg L−1 | 0.9–22.5 | 3.1 | 2.0 | 4.8 | 97 |
| [SPM] | g m−3 | 0.4–4.8 | 1.3 | 0.9 | 1.8 | 97 | |
| aCDOM | m−1 | 0.3–1.2 | 0.42 | 0.38 | 0.49 | 98 | |
| Global RDS | [Chl a] | µg L−1 | 0.02–70.2 | 0.7 | 0.2 | 2.4 | 1982 |
| [SPM] | g m−3 | 0.01–81.2 | 1.9 | 0.8 | 3.8 | 556 | |
| aCDOM | m−1 | 0.001–0.6 | 0.06 | 0.03 | 0.14 | 860 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kratzer, S.; Moore, G. Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans. Remote Sens. 2018, 10, 418. https://doi.org/10.3390/rs10030418
Kratzer S, Moore G. Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans. Remote Sensing. 2018; 10(3):418. https://doi.org/10.3390/rs10030418
Chicago/Turabian StyleKratzer, Susanne, and Gerald Moore. 2018. "Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans" Remote Sensing 10, no. 3: 418. https://doi.org/10.3390/rs10030418
APA StyleKratzer, S., & Moore, G. (2018). Inherent Optical Properties of the Baltic Sea in Comparison to Other Seas and Oceans. Remote Sensing, 10(3), 418. https://doi.org/10.3390/rs10030418