Toward Long-Term Aquatic Science Products from Heritage Landsat Missions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Atmospheric Correction
2.2. Vicarious Calibration
2.2.1. Landsat-7 (ETM+)
2.2.2. Landsat-5 (TM)
2.3. Gain Adjustments
3. Results
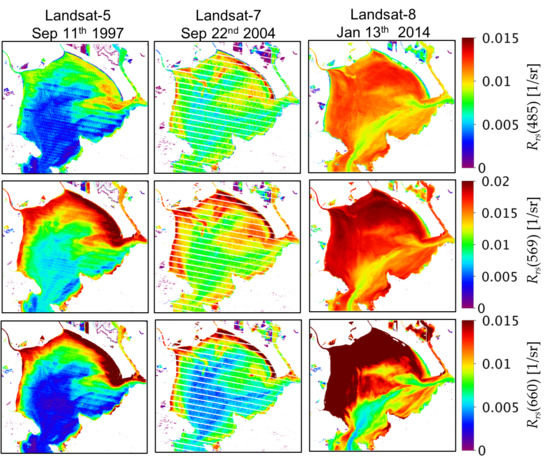
3.1. Qualitative Assessment of Rrs Products
3.2. Validation
3.2.1. AERONET-OC
3.2.2. MODIS-Derived Rrs Products
3.3. Time-Series Applications
4. Discussions: Product Quality
4.1. Signal-to-Noise Ratio (SNR)
4.2. Image Artifacts and Processing Flaws
4.3. Adjacency Effects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Williams, D.L.; Irons, J.R. Landsat sensor performance: History and current status. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2691–2694. [Google Scholar] [CrossRef]
- Schott, J.R. Remote Sensing the Image Chain Approach, 2nd ed.; Oxford University Press: New York, NY, USA, 2007; p. 666. [Google Scholar]
- Gerace, A.D.; Schott, J.R.; Nevins, R. Increased potential to monitor water quality in the near-shore environment with Landsat’s next-generation satellite. J. Appl. Remote Sens. 2013, 7, 073558. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Lee, Z.; Davis, C.O.; Mannino, A.; McClain, C.R.; Franz, B.A. Dynamic range and sensitivity requirements of satellite ocean color sensors: Learning from the past. Appl. Opt. 2012, 51, 6045–6062. [Google Scholar] [CrossRef] [PubMed]
- Helder, D.L.; Markham, B.L.; Thome, K.J.; Barsi, J.A.; Chander, G.; Malla, R. Updated Radiometric Calibration for the Landsat-5 Thematic Mapper Reflective Bands. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3309–3325. [Google Scholar] [CrossRef]
- Markham, B.; Goward, S.; Arvidson, T.; Barsi, J.; Scaramuzza, P. Landsat-7 long-term acquisition plan radiometry-evolution over time. Photogramm. Eng. Remote Sens. 2006, 72, 1129–1135. [Google Scholar] [CrossRef]
- Markham, B.L.; Boncyk, W.C.; Helder, D.L.; Barker, J.L. Landsat-7 Enhanced Thematic Mapper Plus Radiometric Calibration. Can. J. Remote Sens. 1997, 23, 318–332. [Google Scholar] [CrossRef]
- Barnes, B.B.; Hu, C.; Holekamp, K.L.; Blonski, S.; Spiering, B.A.; Palandro, D.; Lapointe, B. Use of Landsat data to track historical water quality changes in Florida Keys marine environments. Remote Sens. Environ. 2014, 140, 485–496. [Google Scholar] [CrossRef]
- IOCCG. Status and Plans for Satellite Ocean-Colour Missions: Considerations for Complementary Missions; Yoder, J.A., Ed.; IOCCG: Dartmouth, NS, Canada, 1999. [Google Scholar]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating Group (IOCCG); IOCCG: Dartmouth, NS, Canada, 2000. [Google Scholar]
- Pahlevan, N.; Schott, J. Leveraging EO-1 to Evaluate Capability of New Generation of Landsat Sensors for Coastal/Inland Water Studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 360–374. [Google Scholar] [CrossRef]
- Helder, D.L.; Ruggles, T.A. Landsat thematic mapper reflective-band radiometric artifacts. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2704–2716. [Google Scholar] [CrossRef]
- Ouillon, S.; Douillet, P.; Andréfouët, S. Coupling satellite data with in situ measurements and numerical modeling to study fine suspended-sediment transport: A study for the lagoon of New Caledonia. Coral Reef. 2004, 23, 109–122. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters. Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [PubMed]
- Doxaran, D.; Froidefond, J.M.; Castaing, P.; Babin, M. Dynamics of the turbidity maximum zone in a macrotidal estuary (the Gironde, France): Observations from field and MODIS satellite data. Estuar. Coast. Shelf Sci. 2009, 81, 321–332. [Google Scholar] [CrossRef]
- Dekker, A.G.; Vos, R.J.; Peters, S.W.M. Comparison of remote sensing data, model results and in situ data for total suspended matter (TSM) in the southern Frisian lakes. Sci. Total Environ. 2001, 268, 197–214. [Google Scholar] [CrossRef]
- Baban, S.M. Detecting water quality parameters in the Norfolk Broads, UK, using Landsat imagery. Int. J. Remote Sens. 1993, 14, 1247–1267. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Cooper, C.M.; Schiebe, F.R. The relationship of MSS and TM digital data with suspended sediments, chlorophyll, and temperature in Moon Lake, Mississippi. Remote Sens. Environ. 1990, 33, 137–148. [Google Scholar] [CrossRef]
- Mertes, L.A.; Smith, M.O.; Adams, J.B. Estimating suspended sediment concentrations in surface waters of the Amazon River wetlands from Landsat images. Remote Sens. Environ. 1993, 43, 281–301. [Google Scholar] [CrossRef]
- Bourgoin, L.M.; Bonnet, M.P.; Martinez, J.M.; Kosuth, P.; Cochonneau, G.; Moreira-Turcq, P.; Guyot, J.L.; Vauchel, P.; Filizola, N.; Seyler, P. Temporal dynamics of water and sediment exchanges between the Curuaí floodplain and the Amazon River, Brazil. J. Hydrol. 2007, 335, 140–156. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Goldschmidt, P.M. Remote sensing of suspended sediment discharge into the western Gulf of Maine during the April 1987 100-year flood. J. Coast. Res. 1992, 8, 218–225. [Google Scholar]
- Dekker, A.G.; Vos, R.; Peters, S. Analytical algorithms for lake water TSM estimation for retrospective analyses of TM and SPOT sensor data. Int. J. Remote Sens. 2002, 23, 15–35. [Google Scholar] [CrossRef]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- Allan, M.G.; Hamilton, D.P.; Hicks, B.J.; Brabyn, L. Landsat remote sensing of chlorophyll a concentrations in central North Island lakes of New Zealand. Int. J. Remote Sens. 2011, 32, 2037–2055. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Pattiaratchi, C.; Lavery, P.; Wyllie, A.; Hick, P. Estimates of water quality in coastal waters using multi-date Landsat Thematic Mapper data. Int. J. Remote Sens. 1994, 15, 1571–1584. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Nieke, B.; Reuter, R.; Heuermann, R.; Wang, H.; Babin, M.; Therriault, J. Light absorption and fluorescence properties of chromophoric dissolved organic matter (CDOM), in the St. Lawrence Estuary (Case 2 waters). Cont. Shelf Res. 1997, 17, 235–252. [Google Scholar] [CrossRef]
- Griffin, C.G.; Frey, K.E.; Rogan, J.; Holmes, R.M. Spatial and interannual variability of dissolved organic matter in the Kolyma River, East Siberia, observed using satellite imagery. J. Geophys. Res. Biogeosci. 2011, 116, G3. [Google Scholar] [CrossRef]
- Phinn, S.; Dekker, A.; Brando, V.E.; Roelfsema, C. Mapping water quality and substrate cover in optically complex coastal and reef waters: An integrated approach. Mar. Pollut. Bullet. 2005, 51, 459–469. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.A. Remote sensing of submerged vegetation canopies for biomass estimation. Int. J. Remote Sens. 1993, 14, 621–627. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Andréfouët, S.; Muller-Karger, F.E.; Hochberg, E.J.; Hu, C.; Carder, K.L. Change detection in shallow coral reef environments using Landsat 7 ETM+ data. Remote Sens. Environ. 2001, 78, 150–162. [Google Scholar] [CrossRef]
- Capolsini, P.; Andréfouët, S.; Rion, C.; Payri, C. A comparison of Landsat ETM+, SPOT HRV, Ikonos, ASTER, and airborne MASTER data for coral reef habitat mapping in South Pacific islands. Can. J. Remote Sens. 2003, 29, 187–200. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Lavery, P.; Pattiaratchi, C.; Wyllie, A.; Hick, P. Water quality monitoring in estuarine waters using the Landsat Thematic Mapper. Remote Sens. Environ. 1993, 46, 268–280. [Google Scholar] [CrossRef]
- Tyler, A.; Svab, E.; Preston, T.; Présing, M.; Kovács, W. Remote sensing of the water quality of shallow lakes: A mixture modelling approach to quantifying phytoplankton in water characterized by high-suspended sediment. Int. J. Remote Sens. 2006, 27, 1521–1537. [Google Scholar] [CrossRef]
- Kutser, T. The possibility of using the Landsat image archive for monitoring long time trends in coloured dissolved organic matter concentration in lake waters. Remote Sens. Environ. 2012, 123, 334–338. [Google Scholar] [CrossRef]
- Lobo, F.L.; Costa, M.P.; Novo, E.M. Time-series analysis of Landsat-MSS/TM/OLI images over Amazonian waters impacted by gold mining activities. Remote Sens. Environ. 2015, 157, 170–184. [Google Scholar] [CrossRef]
- Lyons, M.B.; Roelfsema, C.M.; Phinn, S.R. Towards understanding temporal and spatial dynamics of seagrass landscapes using time-series remote sensing. Estuar. Coast. Shelf Sci. 2013, 120, 42–53. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, H.; Fu, J.; Sheng, G. Water quality change in reservoirs of Shenzhen, China: Detection using LANDSAT/TM data. Sci. Total Environ. 2004, 328, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Erkkilä, A.; Kalliola, R. Patterns and dynamics of coastal waters in multi-temporal satellite images: Support to water quality monitoring in the Archipelago Sea, Finland. Estuar. Coast. Shelf Sci. 2004, 60, 165–177. [Google Scholar] [CrossRef]
- Kallio, K.; Attila, J.; Härmä, P.; Koponen, S.; Pulliainen, J.; Hyytiäinen, U.-M.; Pyhälahti, T. Landsat ETM+ images in the estimation of seasonal lake water quality in boreal river basins. Environ. Manag. 2008, 42, 511–522. [Google Scholar] [CrossRef] [PubMed]
- Hui, F.; Xu, B.; Huang, H.; Yu, Q.; Gong, P. Modelling spatial-temporal change of Poyang Lake using multitemporal Landsat imagery. Int. J. Remote Sens. 2008, 29, 5767–5784. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Andrefouet, S.; Carder, K.L. Atmospheric correction and cross-calibration of LANDSAT-7/ETM+ imagery over aquatic environments: A multiplatform approach using SeaWiFS/MODIS. Remote Sens. Environ. 2001, 78, 99–107. [Google Scholar] [CrossRef]
- Antoine, D.; d’Ortenzio, F.; Hooker, S.B.; Bécu, G.; Gentili, B.; Tailliez, D.; Scott, A.J. Assessment of uncertainty in the ocean reflectance determined by three satellite ocean color sensors (MERIS, SeaWiFS and MODIS-A) at an offshore site in the Mediterranean Sea (BOUSSOLE project). J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Feng, L.; Lee, Z. Uncertainties of SeaWiFS and MODIS remote sensing reflectance: Implications from clear water measurements. Remote Sens. Environ. 2013, 133, 168–182. [Google Scholar] [CrossRef]
- IOCCG. Mission Requirements for Future Ocean-Colour Sensors; Reports of the International Ocean-Colour Coordinating Group; McClain, C.R., Meister, G., Eds.; IOCCG: Dartmuouth, NS, Canada, 2012; p. 102. [Google Scholar]
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Werdell, P.J. Ocean color measurements with the Operational Land Imager on Landsat-8: Implementation and evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. In-orbit calibration strategy for ocean color sensors. Remote Sens. Environ. 1998, 63, 265–278. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Werdell, P.J.; McClain, C.R. Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 2007, 46, 5068–5082. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Z.; Franz, B.A.; McClain, C.R.; Kwiatkowska, E.J.; Werdell, J.; Shettle, E.P.; Holben, B.N. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef] [PubMed]
- Pahlevan, N.; Schott, J.R.; Franz, B.A.; Zibordi, G.; Markham, B.; Bailey, S.; Schaaf, C.B.; Ondrusek, M.; Greb, S.; Strait, C.M. Landsat 8 remote sensing reflectance (Rrs) products: Evaluations, intercomparisons, and enhancements. Remote Sens. Environ. 2017, 190, 289–301. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Pahlevan, N.; Smith, B.; Binding, C.; O’Donnell, D.M. Spectral band adjustments for remote sensing reflectance spectra in coastal/inland waters. Opt. Express 2017, 25, 28650–28667. [Google Scholar] [CrossRef]
- Clark, D.K.; Murphy, M.Y.; Yarbrough, M.; Feinholz, M.; Flora, S.; Broenkow, W.; Bettye, C.J.; Steven, W.B.; Kim, Y.S.; Mueller, J. MOBY, a radiometric buoy for performance monitoring and vicarious calibration of satellite ocean color sensors: Measurement and data analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Mueller, J.L., Giulietta, G.S., McClain, C.R., Eds.; NASA/NOAA/USAF: Greenbelt, MD, USA, 2003; p. 32. [Google Scholar]
- Antoine, D.; Guevel, P.; Deste, J.-F.; Bécu, G.; Louis, F.; Scott, A.J.; Bardey, P. The “BOUSSOLE” buoy-a new transparent-to-swell taut mooring dedicated to marine optics: Design, tests, and performance at sea. J. Atmos. Ocean. Technol. 2008, 25, 968–989. [Google Scholar] [CrossRef]
- Pahlevan, N.; Roger, J.-C.; Ahmad, Z. Revisiting short-wave-infrared (SWIR) bands for atmospheric correction in coastal waters. Opt. Express 2017, 25, 6015–6035. [Google Scholar] [CrossRef] [PubMed]
- Zibordi, G.; Mélin, F.; Berthon, J.-F.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G. AERONET-OC: A network for the validation of ocean color primary products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Bailey, S.W.; Hooker, S.B.; Antoine, D.; Franz, B.A.; Werdell, P.J. Sources and assumptions for the vicarious calibration of ocean color satellite observations. Appl. Opt. 2008, 47, 2035–2045. [Google Scholar] [CrossRef] [PubMed]
- Zibordi, G.; Mélin, F. An evaluation of marine regions relevant for ocean color system vicarious calibration. Remote Sens. Environ. 2017, 190, 122–136. [Google Scholar] [CrossRef] [PubMed]
- Franz, B.A.; Kwiatowska, E.J.; Meister, G.; McClain, C.R. Moderate Resolution Imaging Spectroradiometer on Terra: Limitations for ocean color applications. J. Appl. Remote Sens. 2008, 2, 023525. [Google Scholar] [CrossRef]
- Pahlevan, N.; Schott, J.R. Characterizing the relative calibration of Landsat-7 (ETM+) visible bands with Terra (MODIS) over clear waters: The implications for monitoring water resources. Remote Sens. Environ. 2012, 125, 167–180. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C.; Xiong, X.; Blonski, S.; Wu, A.; Shao, X. Radiometric intercomparison between Suomi-NPP VIIRS and Aqua MODIS reflective solar bands using simultaneous nadir overpass in the low latitudes. J. Atmos. Ocean. Technol. 2013, 30, 2720–2736. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting Simultaneous Nadir Overpasses among Polar-Orbiting Meteorological Satellites for the Intersatellite Calibration of Radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Atmospheric Correction for Remotely-Sensed Ocean-Colour Products; Reports and Monographs of the International Ocean-Colour Coordinating Group (IOCCG); Wang, M. (Ed.) International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2010. [Google Scholar]
- Aurin, D.; Mannino, A.; Franz, B. Spatially resolving ocean color and sediment dispersion in river plumes, coastal systems, and continental shelf waters. Remote Sens. Environ. 2013, 137, 212–225. [Google Scholar] [CrossRef]
- Pahlevan, N.; Lee, Z.; Wei, J.; Schaff, C.; Schott, J.; Berk, A. On-orbit radiometric characterization of OLI (Landsat-8) for applications in aquatic remote sensing. Remote Sens. Environ. 2014, 154, 272–284. [Google Scholar] [CrossRef]
- Esaias, W.E.; Abbott, M.R.; Barton, I.; Brown, O.B.; Campbell, J.W.; Carder, K.L.; Clark, D.K.; Evans, R.H.; Hoge, F.E.; Gordon, H.R. An overview of MODIS capabilities for ocean science observations. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1250–1265. [Google Scholar] [CrossRef] [Green Version]
- Carder, K.; Chen, F.R.; Lee, Z.; Hawes, S.K.; Cannizzaro, J.P. MODIS Ocean Science Team: Algorithm Theoretical Basis Document-ATBD19; College of Marine Science, University of South Florida: Tampa, FL, USA, 2003. [Google Scholar]
- Zhang, H.; Roy, D.P. Landsat 5 Thematic Mapper reflectance and NDVI 27-year time series inconsistencies due to satellite orbit change. Remote Sens. Environ. 2016, 186, 217–233. [Google Scholar]














| Blue [nm] | Green [nm] | Red [nm] | NIR [nm] | SWIR-I [nm] | SWIR-II [nm] | |
|---|---|---|---|---|---|---|
| OLI | 482 | 561 | 655 | 865 | 1609 | 2201 |
| ETM+ | 478 | 560 | 661 | 835 | 1648 | 2205 |
| TM | 485 | 569 | 660 | 840 | 1676 | 2223 |
| Sensor | Blue | Green | Red | NIR | SWIR-I | SWIR-II |
|---|---|---|---|---|---|---|
| ETM+ | 1.030 (0.023) | 1.01 (0.021) | 1.0278 (0.022) | 1.002 (0.008) | 0.964 (0.12) | 0.991 (0.15) |
| TM | 1.047 (0.02) | 1.011 (0.024) | 1.0581 (0.032) | 0.956 (0.011) | 1.095 (0.13) | 1.0151 (0.072) |
| Sensor | Blue | Green | Red | NIR | SWIR-I |
|---|---|---|---|---|---|
| ETM+ | 1.034 | 1.012 | 1.039 | 0.992 | 1.12 |
| TM | 1.059 | 1.011 | 1.058 | 0.931 | 1.21 |
| Band Center [nm] | MRD [%] | RMSE [1/sr] | Slope | Intercept | Bias [1/sr] | R2 |
|---|---|---|---|---|---|---|
| Landsat-7 (ETM+) | ||||||
| 478 | 9.81 (−33.8) | 0.0018 (0.0022) | 1.25 | −0.000016 | 0.0006 | 0.79 |
| 560 | 3.4 (−7.9) | 0.0013 (0.0015) | 1.10 | −0.000024 | 0.000099 | 0.81 |
| 661 | 1.07 (−46.5) | 0.00076 (0.0011) | 1.18 | −0.000014 | 0.0000111 | 0.64 |
| Landsat-5 (TM) | ||||||
| 485 | 13.6 (−85.5) | 0.0020 (0.006) | 1.17 | 0.000013 | 0.00072 | 0.56 |
| 569 | 11.9 (−14.7) | 0.0016 (0.002) | 1.04 | 0.00101 | 0.00082 | 0.85 |
| 660 | 10.1 (−116.2) | 0.00101 (0.003) | 1.14 | 0.0002 | 0.00011 | 0.59 |
| Band Center [nm] | MRD [%] | RMSD [1/sr] | Slope | Intercept | Bias [1/sr] | R2 |
|---|---|---|---|---|---|---|
| Landsat-7 (ETM+) | ||||||
| 478 | −9.56 | 0.00152 | 0.923 | −0.000017 | −0.00044 | 0.91 |
| 560 | −3.29 | 0.00103 | 1.007 | −0.00021 | −0.0002 | 0.97 |
| 661 | −8.15 | 0.00102 | 0.939 | −0.000057 | −0.000039 | 0.98 |
| Landsat-5 (TM) | ||||||
| 485 | −7.11 | 0.002283 | 0.984 | −0.00025 | −0.00033 | 0.76 |
| 569 | −1.83 | 0.001708 | 1.012 | −0.000048 | −0.00017 | 0.93 |
| 660 | 1.97 | 0.001905 | 0.981 | 0.000228 | 0.0000361 | 0.91 |
| Band (nm) | 485 | 569 | 660 | 840 | 1676 | |||
|---|---|---|---|---|---|---|---|---|
| SNR | SNR | SNR | SNR | |||||
| TM | 71.8 | 42.3 | 29.0 | 16.6 | 10.3 | |||
| ETM+ | 77.9 | 69.7 | 40.7 | 13.2 | 10.3 | |||
| OLI | 382.8 | 256.9 | 135.1 | 58.9 | 17.6 | |||
| MODIS | 2209.2 | 2401.8 | 1422.0 | 994.5 | 31.5 | |||
| 54.2 | 29.9 | 15.2 | 4.3 | 0.30 | ||||
| 0.0031 | 0.0028 | 0.0028 | NA | NA | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pahlevan, N.; Balasubramanian, S.V.; Sarkar, S.; Franz, B.A. Toward Long-Term Aquatic Science Products from Heritage Landsat Missions. Remote Sens. 2018, 10, 1337. https://doi.org/10.3390/rs10091337
Pahlevan N, Balasubramanian SV, Sarkar S, Franz BA. Toward Long-Term Aquatic Science Products from Heritage Landsat Missions. Remote Sensing. 2018; 10(9):1337. https://doi.org/10.3390/rs10091337
Chicago/Turabian StylePahlevan, Nima, Sundarabalan V. Balasubramanian, Sudipta Sarkar, and Bryan A. Franz. 2018. "Toward Long-Term Aquatic Science Products from Heritage Landsat Missions" Remote Sensing 10, no. 9: 1337. https://doi.org/10.3390/rs10091337
APA StylePahlevan, N., Balasubramanian, S. V., Sarkar, S., & Franz, B. A. (2018). Toward Long-Term Aquatic Science Products from Heritage Landsat Missions. Remote Sensing, 10(9), 1337. https://doi.org/10.3390/rs10091337