Optimal Interpolation of Precipitable Water Using Low Earth Orbit and Numerical Weather Prediction Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
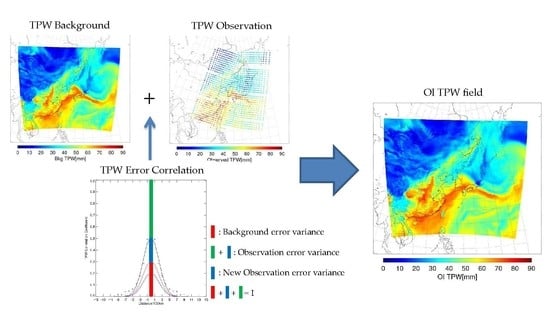
2.2. Optimal Interpolation Procedure
2.3. Estimation of Error Variances
2.4. The New Approach: Considering Off-Diagonal Components
3. Results
3.1. Correlation Length Scales and Error Variances
3.2. Optimal Interpolation Precipitable Water Fields
3.3. Validation
4. Discussion
4.1. Satellite-Based and Numerical Weather Prediction-Forecasted Precipitable Water Data
4.2. Error Covariance
4.3. Optimal Interpolation Process for the High Layer
4.4. Bias Correction
4.5. Operations in Near Real Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Forsythe, J.M.; Kidder, S.Q.; Fuell, K.K.; LeRoy, A.; Jedlovec, G.J.; Jones, A.S. A multisensor, blended, layered water vapor product for weather analysis and forecasting. J. Oper. Meteor. 2015, 3, 41–58. [Google Scholar] [CrossRef]
- Kidder, S.Q.; Jones, A.S. A Blended Satellite Total Precipitable Water Product for Operational Forecasting. J. Atmos. Ocean. Technol. 2007, 24, 74–81. [Google Scholar] [CrossRef]
- Eyre, J.R. Inversion of cloudy satellite sounding radiances by nonlinear optimal estimation. I: Theory and simulation for TOVS. Q. J. R. Meteor. Soc. 1989, 115, 1001–1026. [Google Scholar] [CrossRef]
- Li, J.; Wolf, W.W.; Menzel, P.; Zhang, W.; Huwang, H.-L.; Achtor, T.H. Global Soundings of the Atmosphere from ATOVS Measurements: The Algorithm and Validation. J. Appl. Meteor. 2000, 39, 1248–1268. [Google Scholar] [CrossRef]
- Li, J.; Martinez, M.A.; Manso, M.; Velazquez, M.; Cuevas, G. Physical retrieval algorithm development for operational SEVIRI clear sky nowcasting products. In Proceedings of the 2008 EUMETSAT Meteorological Satellite Data User’s Conference, Darmstadt, Germany, 8–12 September 2008. [Google Scholar]
- Gambacorta, A.; Barnet, C.; Wolf, W.; Goldberg, M.; King, T.; Nalli, N.; Maddy, E.; Xiong, X.; Divakarla, M. The NOAA Unique CrIS/ATMS Processing System (NUCAPS): Fist Light Results. In Proceedings of the ITWG Meeting, Toulouse, France, 20 March 2012. [Google Scholar]
- Bouttier, F.; Courtier, P. Data assimilation concepts and methods March 1999. ECMWF. 2002, pp. 1–59. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2002/16928-data-assimilation-concepts-and-methods.pdf (accessed on 10 March 2018).
- Schulz, J.; Lindau, R. Towards and Optimal Merging of Satellite Data Sets. 15 January 2014. Available online: https://www.researchgate.net/publication/228686783 (accessed on 24 February 2018).
- Lee, C.S.; Park, J.D.; Shin, J.; Jang, J.-D. Improvement of AMSR2 Soil Moisture Products over South Korea. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3839–3849. [Google Scholar] [CrossRef]
- Courtier, P.; Andersson, E.; Heckley, W.; Pailleux, J.; Vasiljevic, D.; Hamrud, M.; Hollingsworth, A.; Rabier, F.; Fisher, M. The ECMWF implementation of three-dimensional variational assimilation (3D-Var). Part 1: Formulation. Q. J. R. Meteor. Soc. 1998, 124, 1783–1807. [Google Scholar]
- Hollingsworth, A.; Lonnberg, P. The statistical structure of short-range forecast errors as determined from radiosonde data. Part 1: The wind field. Tellus 1986, 38, 111–136. [Google Scholar] [CrossRef]
- Smith, N.; Berndt, E.; Zavodsky, B.; Pierce, B.; Davies, J.; Hoese, D.; White, K.; Frost, G.; McKeen, S.; Wheeler, A.; et al. The Value of CSPP NUCAPS in Real-Time Applications. In Proceedings of the CSPP/IMAPP Users Group Metting, Madison, WI, USA, 27–29 June 2017. [Google Scholar]
- Shepard, M.W.; Cady-Pereira, K.E. Cross-track Infrared Sounder (CrIS) satellite observations of tropospheric ammonia. Atmos. Meas. Technol. 2015, 8, 1323–1335. [Google Scholar] [CrossRef]
- Numerical forecasting takes responsibility for the weather and climate industries!–Utilization guide of Numerical Weather Prediction model data for activation of the weather industry. Numerical Modeling Center of the Korea Meteorological Administration: Seoul, Korea, 2013; publication report number: 11–1360395-000252-01.
- Ghil, M. Meteorological Data Assimilation for Oceanographers. Part I: Description and Theoretical Framework. Dyn. Atmos. Oceans 1989, 13, 171–218. [Google Scholar] [CrossRef]
- Lorence, A. Analysis methods for numerical weather prediction. Q. J. R. Meteor. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Daley, R. Atmospheric Data Analysis; Cambridge Atmospheric and Space Science Series; Cambridge University Press: Cambridge, UK, 1991; p. 457. ISBN 0-521-38215-7. [Google Scholar]
- Hollingsworth, A.; Shaw, D.; Lonnberg, P.; Illari, L.; Arpe, K.; Simmons, A. Monitoring of observation and analysis quality by a data-assimilation system. Mon. Weather Rev. 1986, 114, 1225–1242. [Google Scholar] [CrossRef]
- Parrish, D.; Derber, J. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Ide, K.; Courtier, P.; Ghil, M.; Lorence, A.C. Unified Notation for Data Assimilation:Operational, Sequential and Variational. J. Meteor. Soc. Japan 1997, 75, 181–189. [Google Scholar] [CrossRef]
- Rodgers, C.D. Retrieval of atmospheric temperature and composition from remote measurements of thermal radiation. Rev. Geophys. Space Phys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.-L. Retrieval of atmospheric profiles from satellite sounder measurements by use of the discrepancy principle. Appl. Opt. 1999, 38, 916–923. [Google Scholar] [CrossRef] [PubMed]
- Martinez, M.A. Algorithm Theoretical Basis Document for “SEVIRI Physical Retrieval Product” (SPhR-PGE13 v2.0); AEMET: Madrid, Spain, 2013. [Google Scholar]
- Choi, Y.; Ha, J.C.; Lim, G.H. Inverstigation of the Effects of Considering Ballon Drift Information on Radisonde Data Assimilation Using the Four-Dimensional Variational Method. Weather Forecast. 2015, 30, 809–826. [Google Scholar] [CrossRef]
- Davies, T.; Cullen, M.J.P.; Malcolm, A.J.; Mawson, M.H.; Staniforth, A.; White, A.A.; Wood, N. A new dynamical core for the Met Office’s global and regional modeling of the atmosphere. Q. J. R. Meteor. Soc. 2015, 131, 1759–1782. [Google Scholar] [CrossRef]
- McGrath, R.; Semmler, T.; Sweeney, C.; Wang, S. Impact of balloon drift errors in radiosonde data on climate statistics. J. Clim. 2006, 19, 3430–3442. [Google Scholar] [CrossRef]
- Laroche, S.; Sarrazin, R. Impact of radiosonde balloon drift on numerical weather prediction and verification. Weather Forecast. 2013, 28, 772–782. [Google Scholar] [CrossRef]
- MacPherson, B. Radiosonde balloon drift—Does it matter for data assimilation? Meteor. Appl. 1995, 2, 301–305. [Google Scholar] [CrossRef]
- Martinez, M.A.; Romero, R. Validation Report for “SEVIRI Physical Retrieval Product” (SPhR-PGE13) v1.2; AEMET: Madrid, Spain, 2012. [Google Scholar]
- Kusselson, S.J.; Kidder, S.Q.; Forsythe, J.M.; Jones, A.S.; Zhao, L. An update on the operational implementation of blended total precipitable water. In Proceedings of the 23rd Conference on Hydrology, Phoenix, AZ, USA, 11–15 January 2009. [Google Scholar]








| Satellite | Overpass Time above Korea (UTC) | Horizontal Resolution (km) | Vertical Resolution (km) |
|---|---|---|---|
| MetOp-A | 01:24, 11:10, 12:56 | 126 | 1~2 |
| MetOp-B | 00:39, 02:25, 12:04 | 126 | 1~2 |
| NOAA-18 | 09:28, 21:41, 23:35 | 126 | 1~2 |
| NOAA-19 | 05:24, 06:30, 17:56 | 126 | 1~2 |
| Suomi-NPP | 03:25, 04:24, 16:57, 18:40 | 41 | 1~2 |
| Variable | , | |||||
|---|---|---|---|---|---|---|
| MetOp | ||||||
| TPW | 24.03 | 47.21 | 13.50 | 26.52 | 3.90 | 339.83 |
| BL | 13.32 | 20.50 | 4.88 | 7.51 | 0.00 | 636.37 |
| ML | 14.30 | 17.06 | 8.08 | 9.64 | 0.00 | 510.36 |
| HL | 1.25 | 0.90 | 0.60 | 0.43 | 0.00 | 981.69 |
| NOAA | ||||||
| TPW | 22.03 | 49.59 | 10.59 | 23.84 | 7.02 | 454.82 |
| BL | 13.88 | 22.32 | 4.52 | 7.27 | 0.00 | 636.37 |
| ML | 15.89 | 17.51 | 7.46 | 8.22 | 1.50 | 453.97 |
| HL | 0.94 | 1.05 | 0.40 | 0.45 | 0.03 | 657.07 |
| NPP | ||||||
| TPW | 20.06 | 83.41 | 15.31 | 63.67 | 21.83 | 636.37 |
| BL | 33.53 | 32.71 | 22.81 | 22.25 | 2.84 | 636.37 |
| ML | 14.43 | 18.41 | 11.45 | 14.61 | 1.82 | 751.08 |
| HL | 1.13 | 0.73 | 0.34 | 0.22 | 0.00 | 595.79 |
| Variable | RMSE (mm) | Bias (mm) | ||||
|---|---|---|---|---|---|---|
| Bkg | Obs | OI | Bkg | Obs | OI | |
| TPW | 3.58 | 5.11 | 3.79 | −0.23 | −0.21 | 0.30 |
| BL | 2.49 | 3.13 | 2.32 (6.91%) | −1.32 | −0.95 | −0.51 (61.75%) |
| ML | 2.85 | 3.09 | 2.73 (4.15%) | 1.69 | 0.08 | 1.21 (28.07%) |
| HL | 0.72 | 0.65 | 0.66 (8.00%) | −0.36 | 0.06 | −0.03 (91.19%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, J.-H.; Ryu, G.-H.; Jang, J.-D. Optimal Interpolation of Precipitable Water Using Low Earth Orbit and Numerical Weather Prediction Data. Remote Sens. 2018, 10, 436. https://doi.org/10.3390/rs10030436
Heo J-H, Ryu G-H, Jang J-D. Optimal Interpolation of Precipitable Water Using Low Earth Orbit and Numerical Weather Prediction Data. Remote Sensing. 2018; 10(3):436. https://doi.org/10.3390/rs10030436
Chicago/Turabian StyleHeo, Jun-Hyung, Geun-Hyeok Ryu, and Jae-Dong Jang. 2018. "Optimal Interpolation of Precipitable Water Using Low Earth Orbit and Numerical Weather Prediction Data" Remote Sensing 10, no. 3: 436. https://doi.org/10.3390/rs10030436
APA StyleHeo, J. -H., Ryu, G. -H., & Jang, J. -D. (2018). Optimal Interpolation of Precipitable Water Using Low Earth Orbit and Numerical Weather Prediction Data. Remote Sensing, 10(3), 436. https://doi.org/10.3390/rs10030436