An Efficient Maximum Likelihood Estimation Approach of Multi-Baseline SAR Interferometry for Refined Topographic Mapping in Mountainous Areas
Abstract
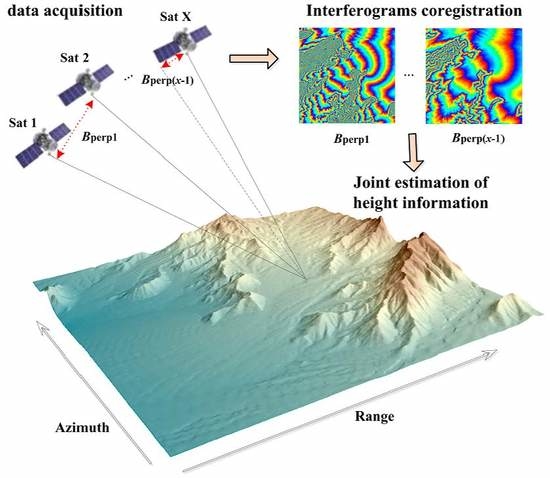
:1. Introduction
2. Maximum Likelihood Height Estimation Assisted by Prior DEM
2.1. Basic Principle
2.2. Definition of the Prior Height Probability
3. Optimized Processing Flow for Spaceborne Multi-Baseline InSAR Datasets
3.1. Interferometric Processing
3.2. Maximum Likelihood Height Estimation with the Prior DEM
3.2.1. Rational Function Model (RFM) for Height-to-Phase Conversion
3.2.2. Height Likelihood Probability Lookup Table
3.2.3. ML Height Estimation with Flexible Search Step Length
- (1)
- Obtain the initial height value from the prior DEM, which is radar-coded to the SAR image coordinates;
- (2)
- Set the height search range to and the search step to . can be set to an integral multiple of . The optimal height obtained by the maximum likelihood estimation is ;
- (3)
- The height search range becomes and the search step is . The optimal height obtained by the maximum likelihood estimation is ;
- (4)
- Test whether is less than the given threshold. If yes, then stop the search and return as the optimal height. If no, then repeat Step (3).
3.3. Geocoding
4. Experiments and Results
4.1. Simulated Experiment
4.1.1. Simulation of SAR Interferograms
4.1.2. Test of the Impact of the Prior Height on ML Estimation
4.1.3. Test of the Impact of the Atmospheric Effects on ML Estimation
4.2. ALOS/PALSAR Data Experiment
4.2.1. Experimental Area
4.2.2. ALOS/PALSAR Data
4.2.3. Elevation Datasets
4.2.4. Experimental Results
5. Discussion
5.1. Comparative Analysis of the Single- and Multi-Baseline InSAR DEMs
5.2. Comparative Analysis of the Prior Height’s Impact on ML Estimation
5.3. Comparative Analysis of the Multi-Baseline InSAR DEM and SRTM DEM
6. Conclusions
- (1)
- The height accuracy of the ML estimation with re-defined prior height probability distribution is much better than that of the ML estimation without prior height probability, indicating that well-defined height probability can suppress phase noise and help solve the height ambiguity problem.
- (2)
- The processing strategy proposed in this article, including (1) replacing the rigorous height-to-phase conversion with the rational function model (RFM); (2) substituting the complicated height likelihood probability function with a two-dimensional lookup table; (3) searching for the maximum likelihood height with flexible search step length instead of the fixed search step length, is effective, making the proposed processing flow applicable to spaceborne datasets.
- (3)
- Compared with SRTM DEM, the multi-baseline InSAR DEM has obvious advantages in terms of resolution and precision. Hence the multi-baseline InSAR estimation can be viewed as a topographical information update of the historical low-resolution DEMs.
- (4)
- The multi-baseline InSAR DEM generated from ALOS/PALSAR datasets meets the American DTED-2 standard and Chinese 1:50,000 DEM (mountain) Level 2 in the case of spatial resolution and height accuracy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zebker, H.A.; Goldstein, R.M. Topographic mapping from interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Zebker, H.A.; Werner, C.L.; Rosen, P.A.; Hensley, S. Accuracy of topographic maps derived from ERS-1 interferometric radar. IEEE Trans. Geosci. Remote Sens. 1994, 32, 823–836. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Xu, L.; Xu, M.; Lou, L.; Xu, H.; Liao, M.; Chen, J.; Yu, W. Spaceborne D-InSAR system: Conceptual overview. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 99–102. [Google Scholar]
- Gao, X.; Liu, Y.; Li, T.; Wu, D. High Precision DEM Generation Algorithm Based on InSAR Multi-Look Iteration. Remote Sens. 2017, 9, 741. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Wahl, D.E. Interferometric synthetic aperture radar terrain elevation mapping from multiple observations. In Proceedings of the IEEE 6th Digital Signal Processing Workshop, Yosemite National Park, CA, USA, 2–5 October 1994; pp. 33–36. [Google Scholar]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Gini, F.; Lombardini, F.; Montanari, M. Layover solution in multi-baseline SAR interferometry. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1344–1356. [Google Scholar] [CrossRef]
- Fornaro, G.; Pauciullo, A.; Sansosti, E. Phase difference-based multichannel phase unwrapping. IEEE Trans. Image Process. 2005, 14, 960–972. [Google Scholar] [CrossRef] [PubMed]
- Ferretti, A.; Prati, C.; Rocca, F.; Monti Guarnieri, A. Multi-baseline SAR interferometry for automatic DEM reconstruction (DEM). In Proceedings of the Third ERS Symposium on Space at the service of our Environment, Florence, Italy, 14–21 March 1997. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Multi-baseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
- Jiang, H.J.; Zhang, L.; Wang, Y.; Liao, M.S. Fusion of high-resolution DEMs derived from COSMO-SkyMed and TerraSAR-X InSAR datasets. J. Geodesy 2014, 88, 587–599. [Google Scholar] [CrossRef]
- Thompson, D.G.; Robertson, A.E.; Arnold, D.V.; Long, D.G. Multi-baseline interferometric SAR for iterative height estimation. In Proceedings of the 1999 IEEE International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; pp. 251–253. [Google Scholar]
- Xia, X.-G.; Wang, G. Phase unwrapping and a robust Chinese remainder theorem. IEEE Signal Process. Lett. 2007, 14, 247–250. [Google Scholar] [CrossRef]
- Yuan, Z.H.; Deng, Y.K.; Li, F.; Wang, R.; Liu, G.; Han, X.L. Multichannel InSAR DEM reconstruction through improved closed-form robust Chinese Remainder Theorem. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1314–1318. [Google Scholar] [CrossRef]
- Lombardo, P.; Lombardini, F. Multi-baseline SAR interferometry for terrain slope adaptivity. In Proceedings of the IEEE National Radar Conference, Syracuse, NY, USA, 13–15 May 1997; pp. 196–201. [Google Scholar]
- Pascazio, V.; Schirinzi, G. Multifrequency InSAR height reconstruction through maximum likelihood estimation of local planes parameters. IEEE Trans. Image Process. 2002, 11, 1478–1489. [Google Scholar] [CrossRef] [PubMed]
- Fornaro, G.; Guarnieri, A.M.; Pauciullo, A.; De-Zan, F. Maximum likelihood multi-baseline SAR interferometry. IEEE Proc. Radar Sonar Navig. 2006, 153, 279–288. [Google Scholar] [CrossRef]
- Eineder, M.; Adam, N. A maximum-likelihood estimator to simultaneously unwrap, geocode, and fuse SAR interferograms from different viewing geometries into one digital elevation model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 24–36. [Google Scholar] [CrossRef]
- Ferraiuolo, G.; Pascazio, V.; Schirinzi, G. Maximum a posteriori estimation of height profiles in InSAR imaging. IEEE Geosci. Remote Sens. Lett. 2004, 1, 66–70. [Google Scholar] [CrossRef]
- Ferraiuolo, G.; Meglio, F.; Pascazio, V.; Schirinzi, G. DEM Reconstruction Accuracy in Multichannel SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 191–201. [Google Scholar] [CrossRef]
- Xiong, S.; Muller, J.-P.; Li, G. The Application of ALOS/PALSAR InSAR to Measure Subsurface Penetration Depths in Deserts. Remote Sens. 2017, 9, 638. [Google Scholar] [CrossRef]
- Pascazio, V.; Schirinzi, G. Estimation of terrain elevation by multifrequency interferometric wide band SAR data. IEEE Signal Process. Lett. 2001, 8, 7–9. [Google Scholar] [CrossRef]
- Tough, R.; Blacknell, D.; Quegan, S. A Statistical Description of Polarimetric and Interferometric Synthetic Aperture Radar Data; Royal Society: London, UK, 1995; pp. 567–589. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Liao, M.; Jiang, H.; Wang, Y.; Wang, T.; Zhang, L. Improved topographic mapping through high-resolution SAR interferometry with atmospheric effect removal. ISPRS J. Photogramm. Remote Sens. 2013, 80, 72–79. [Google Scholar] [CrossRef]
- Zhang, L.; He, X.Y.; Balz, T.; Wei, X.H.; Liao, M.S. Rational function modeling for spaceborne SAR datasets. ISPRS J. Photogramm. Remote Sens. 2011, 66, 133–145. [Google Scholar] [CrossRef]
- National Administration of Surveying, Mapping and Geoinformation of China. National Standards for 1:5000, 1:10,000, 1:25,000, 1:50,000, 1:100,000 Digital Elevation Model; Surveying and Mapping Publishing House: Bejing, China, 2010.
- National Geospatial-Intelligence Agency. Geospatial Standards and Specifications, 2003. Available online: https://www.nga.mil/ProductsServices/TopographicalTerrestrial/Pages/DigitalTerrainElevationData.aspx (accessed on 10 March 2018).












| Spaceborne InSAR Data | Height Ambiguity | Height-To-Phase | |
|---|---|---|---|
| Max. Error | RMSE | ||
| ALOS/PALSAR | 82 m | 1.97 × 10−3° | 2.14 × 10−4° |
| COSMO-SkyMed | 164 m | −4.08 × 10−4° | 6.78 × 10−5° |
| TerraSAR-X | 59 m | −1.81 × 10−3° | 2.15 × 10−4° |
| Interferogram I | Interferogram II | Interferogram III | |
|---|---|---|---|
| Normal baseline | 47 m | 83 m | 178 m |
| Height ambiguity | 139.54 m | 79.02 m | 36.84 m |
| Coherence coefficient | 0.60 | 0.57 | 0.51 |
| Std. of phase noise | 0.254 rad | 0.277 rad | 0.333 rad |
| Mean | Std. | |
|---|---|---|
| Prior DEM | 0.007 m | 4.7 m |
| Interferogram I (Figure 3d) | 0.002 m | 5.6 m |
| Interferogram II (Figure 3e) | −0.010 m | 3.5 m |
| Interferogram III (Figure 3f) | −0.001 m | 2.0 m |
| ML without prior DEM | 70.072 m | 408.8 m |
| ML with prior DEM | −0.003 m | 1.6 m |
| Mean | Std. | |
|---|---|---|
| Interferogram I (Figure 3j) | −2.5 m | 16.2 m |
| Interferogram II (Figure 3k) | 2.5 m | 8.7 m |
| Interferogram III (Figure 3l) | −0.6 m | 4.6 m |
| ML with prior DEM | −0.006 m | 4.1 m |
| Acquisition Time | 22 December 2007/6 February 2008/23 March 2008/ 27 December 2009/11 February 2010/29 March 2010 |
|---|---|
| Orbit direction | Ascending |
| Imaging mode | Stripmap |
| Polarization | HH |
| Central incidence angle | 38.7° |
| Sampling space of azimuth/range direction | 3.18 m/4.68 m |
| Band width of azimuth/range direction | 1522 Hz/28 MHz |
| Interferogram I | Interferogram II | Interferogram III | Interferogram IV | |
|---|---|---|---|---|
| Acquisition time of the Master image | 6 February 2008 | 6 February 2008 | 11 February 2010 | 11 February 2010 |
| Acquisition time of the Slave image | 22 December 2007 | 23 March 2008 | 27 December 2009 | 29 March 2010 |
| Temporal baseline | 46 days | 46 days | 46 days | 46 days |
| Normal baseline | −784 m | 77 m | −561 m | 185 m |
| Height ambiguity | 82 m | 833 m | 115 m | 347 m |
| Central Doppler frequency | 74/75 Hz | 74/80 Hz | 68/57 Hz | 68/46 Hz |
| Mean coherence coefficient | 0.52 | 0.53 | 0.58 | 0.50 |
| Mean | Std. | Absolute Value ≤ 10 m | |
|---|---|---|---|
| SRTM DEM | 4.9 m | 15.4 m | 58.9% |
| Interferogram I DEM | 1.9 m | 11.3 m | 81.4% |
| Interferogram II DEM | −4.4 m | 43.0 m | 32.8% |
| Interferogram III DEM | 2.3 m | 10.6 m | 83.0% |
| Interferogram IV DEM | −0.3 m | 27.7 m | 51.8% |
| multi-baseline DEM | 1.7 m | 8.6 m | 86.3% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Jiang, H.; Zhang, L.; Liao, M. An Efficient Maximum Likelihood Estimation Approach of Multi-Baseline SAR Interferometry for Refined Topographic Mapping in Mountainous Areas. Remote Sens. 2018, 10, 454. https://doi.org/10.3390/rs10030454
Dong Y, Jiang H, Zhang L, Liao M. An Efficient Maximum Likelihood Estimation Approach of Multi-Baseline SAR Interferometry for Refined Topographic Mapping in Mountainous Areas. Remote Sensing. 2018; 10(3):454. https://doi.org/10.3390/rs10030454
Chicago/Turabian StyleDong, Yuting, Houjun Jiang, Lu Zhang, and Mingsheng Liao. 2018. "An Efficient Maximum Likelihood Estimation Approach of Multi-Baseline SAR Interferometry for Refined Topographic Mapping in Mountainous Areas" Remote Sensing 10, no. 3: 454. https://doi.org/10.3390/rs10030454
APA StyleDong, Y., Jiang, H., Zhang, L., & Liao, M. (2018). An Efficient Maximum Likelihood Estimation Approach of Multi-Baseline SAR Interferometry for Refined Topographic Mapping in Mountainous Areas. Remote Sensing, 10(3), 454. https://doi.org/10.3390/rs10030454