Estimating Sub-Pixel Soybean Fraction from Time-Series MODIS Data Using an Optimized Geographically Weighted Regression Model
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Sample Data
2.3. Feature Set
2.4. Census Data
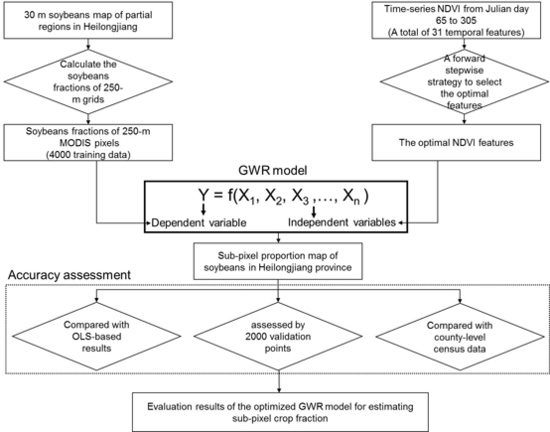
3. Methodology
3.1. An Optimized Geographically Weighted Regression Model
3.1.1. The Basic Framework of GWR Model
3.1.2. A Forward Stepwise Strategy for Selecting the Optimal Independent Variables
- Step 1: Start by calibrating all possible bivariate GW regressions by in turn regressing a single explanatory variable against the dependent variable. Calculate AICc in each case (31 runs in this study). Select the variable that produces the lowest AICc.
- Step 2: Sequentially introduce a variable from the remaining n − 1 features to construct new models with the permanently included independent variable in step 1. Calculate the change in AICc between step1 and step 2. Select variable yielding greatest reduction in AICc. Add this variable to the model.
- Step 3: Repeat step 2 until no independent variables among the candidate variables can be added into the model, and the model at this point is the final model.
3.1.3. F-Test Statistics
3.2. Accuracy Assessment
4. Results
4.1. Descriptive Statistics
4.2. The Optimal Independent Variables for Soybean Cultivation
4.3. GWR Results of Sub-Pixel Soybean Area Estimation
4.4. Sub-Pixel Soybean Map and Accuracy Assessment
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhong, L.; Gong, P.; Biging, G.S. Efficient corn and soybean mapping with temporal extendability: A multi-year experiment using landsat imagery. Remote Sens. Environ. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Monfreda, C.; Ramankutty, N.; Foley, J.A. Farming the planet: 2. Geographic distribution of crop areas, yields, physiological types, and net primary production in the year 2000. Glob. Biogeochem. Cycles 2008, 22, GB1022. [Google Scholar] [CrossRef]
- Zheng, H.; Chen, L.; Han, X.; Zhao, X.; Ma, Y. Classification and regression tree (cart) for analysis of soybean yield variability among fields in northeast china: The importance of phosphorus application rates under drought conditions. Agric. Ecosyst. Environ. 2009, 132, 98–105. [Google Scholar] [CrossRef]
- Sun, J.; Wu, W.; Tang, H.; Liu, J. Spatiotemporal patterns of non-genetically modified crops in the era of expansion of genetically modified food. Sci. Rep. 2015, 5, 14180. [Google Scholar] [CrossRef] [PubMed]
- Wardlow, B.; Egbert, S.; Kastens, J. Analysis of time-series MODIS 250 m vegetation index data for crop classification in the u.S. Central great plains. Remote Sens. Environ. 2007, 108, 290–310. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, W.; Song, Q.; Yu, Q.; Lu, M.; Yang, P.; Tang, H.; Long, Y. Extending the pairwise separability index for multicrop identification using time-series MODIS images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6349–6361. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, W.-B.; Song, Q.; Lu, M.; Chen, D.; Yu, Q.-Y.; Tang, H.-J. How do temporal and spectral features matter in crop classification in heilongjiang province, china? J. Integr. Agric. 2017, 16, 324–336. [Google Scholar] [CrossRef]
- Chang, J.; Hansen, M.C.; Pittman, K.; Carroll, M.; DiMiceli, C. Corn and soybean mapping in the united states using MODIS time-series data sets. Agron. J. 2007, 99, 1654. [Google Scholar] [CrossRef]
- Huang, X.; Schneider, A.; Friedl, M.A. Mapping sub-pixel urban expansion in china using MODIS and DMSP/OLS nighttime lights. Remote Sens. Environ. 2016, 175, 92–108. [Google Scholar] [CrossRef]
- Pan, Y.; Li, L.; Zhang, J.; Liang, S.; Zhu, X.; Sulla-Menashe, D. Winter wheat area estimation from MODIS-evi time series data using the crop proportion phenology index. Remote Sens. Environ. 2012, 119, 232–242. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P. Cropland distributions from temporal unmixing of MODIS data. Remote Sens. Environ. 2004, 93, 412–422. [Google Scholar] [CrossRef]
- Atzberger, C.; Rembold, F. Mapping the spatial distribution of winter crops at sub-pixel level using avhrr ndvi time series and neural nets. Remote Sens. 2013, 5, 1335–1354. [Google Scholar] [CrossRef] [Green Version]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Löw, F.; Michel, U.; Dech, S.; Conrad, C. Impact of feature selection on the accuracy and spatial uncertainty of per-field crop classification using support vector machines. ISPRS J. Photogramm. Remote Sens. 2013, 85, 102–119. [Google Scholar] [CrossRef]
- Drumetz, L.; Chanussot, J.; Jutten, C. Variability of the endmembers in spectral unmixing: Recent advances. In Proceedings of the 8th IEEE Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Los Angeles, CA, USA, 21–24 August 2016. [Google Scholar]
- Zhang, L.; Wei, Y.; Meng, R. Spatiotemporal dynamics and spatial determinants of urban growth in Suzhou, China. Sustainability 2017, 9, 393. [Google Scholar] [CrossRef]
- Propastin, P.A. Spatial non-stationarity and scale-dependency of prediction accuracy in the remote estimation of lai over a tropical rainforest in sulawesi, indonesia. Remote Sens. Environ. 2009, 113, 2234–2242. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Li, W.; Si, M. Viirs-based remote sensing estimation of ground-level PM2.5 concentrations in Beijing–Tianjin–Hebei: A spatiotemporal statistical model. Remote Sens. Environ. 2016, 184, 316–328. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- You, W.; Zang, Z.; Zhang, L.; Li, Z.; Chen, D.; Zhang, G. Estimating ground-level PM10 concentration in northwestern china using geographically weighted regression based on satellite aod combined with calipso and MODIS fire count. Remote Sens. Environ. 2015, 168, 276–285. [Google Scholar] [CrossRef]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-based ground PM2.5 estimation using timely structure adaptive modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Perger, C.; Schill, C.; Zhao, Y.; Maus, V.; et al. Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS J. Photogramm. Remote Sens. 2015, 103, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Wu, W.; Xia, T.; Yu, Q.; Yang, P.; Li, Z.; Song, Q. Exploring the use of google earth imagery and object-based methods in land use/cover mapping. Remote Sens. 2013, 5, 6026–6042. [Google Scholar] [CrossRef]
- Agriculture, C.M.O. China Agricultural Statistics Yearbook; China Statistics Press: Beijing, China, 2015. [Google Scholar]
- Rui, X.; Zhongjun, L.; Yang, L.; Bin, F.; Kebao, L. Comparison on linear feature real width and interpretation width using landsat tm8 images and gf-1 images. Trans. Chin. Soc. Agric. Eng. 2015, 16. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. Large-area crop mapping using time-series MODIS 250 m ndvi data: An assessment for the u.S. Central great plains. Remote Sens. Environ. 2008, 112, 1096–1116. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A pok-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Lesiv, M.; Moltchanova, E.; Schepaschenko, D.; See, L.; Shvidenko, A.; Comber, A.; Fritz, S. Comparison of data fusion methods using crowdsourced data in creating a hybrid forest cover map. Remote Sens. 2016, 8, 261. [Google Scholar] [CrossRef]
- Salas, C.; Ene, L.; Gregoire, T.G.; Næsset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistical models. Remote Sens. Environ. 2010, 114, 1277–1285. [Google Scholar] [CrossRef]
- Guo, L.; Ma, Z.; Zhang, L. Comparison of bandwidth selection in application of geographically weighted regression: A case study. Can. J. Forest Res. 2008, 38, 2526–2534. [Google Scholar] [CrossRef]
- Gollini, I.; Lu, B.B.; Charlton, M.; Brunsdon, C.; Harris, P. Gwmodel: An r package for exploring spatial heterogeneity using geographically weighted models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef]
- Leung, Y.; Mei, C.L.; Zhang, W.X. Statistical tests for spatial nonstationarity based on the geographically weighted regression model. Environ. Plan. A 2000, 32, 9–32. [Google Scholar] [CrossRef]
- Maxwell, S.K.; Nuckols, J.R.; Ward, M.H.; Hoffer, R.M. An automated approach to mapping corn from landsat imagery. Comput. Electron. Agric. 2004, 43, 43–54. [Google Scholar] [CrossRef]
- Xiao, X.; Boles, S.; Frolking, S.; Li, C.; Babu, J.Y.; Salas, W.; Moore, B. Mapping paddy rice agriculture in south and southeast asia using multi-temporal MODIS images. Remote Sens. Environ. 2006, 100, 95–113. [Google Scholar] [CrossRef]
- Colditz, R.R.; López Saldaña, G.; Maeda, P.; Espinoza, J.A.; Tovar, C.M.; Hernández, A.V.; Benítez, C.Z.; Cruz López, I.; Ressl, R. Generation and analysis of the 2005 land cover map for mexico using 250 m MODIS data. Remote Sens. Environ. 2012, 123, 541–552. [Google Scholar] [CrossRef]
- Mei, C.L.; He, S.Y.; Fang, K.T. A note on the mixed geographically weighted regression model. J. Reg. Sci. 2004, 44, 143–157. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Schepaschenko, D.; See, L.; Lesiv, M.; McCallum, I.; Fritz, S.; Salk, C.; Moltchanova, E.; Perger, C.; Shchepashchenko, M.; Shvidenko, A.; et al. Development of a global hybrid forest mask through the synergy of remote sensing, crowdsourcing and fao statistics. Remote Sens. Environ. 2015, 162, 208–220. [Google Scholar] [CrossRef]
- Torbick, N.; Chowdhury, D.; Salas, W.; Qi, J. Monitoring rice agriculture across myanmar using time series sentinel-1 assisted by landsat-8 and palsar-2. Remote Sens. 2017, 9, 119. [Google Scholar] [CrossRef]
- Radoux, J.; Chomé, G.; Jacques, D.; Waldner, F.; Bellemans, N.; Matton, N.; Lamarche, C.; d’Andrimont, R.; Defourny, P. Sentinel-2’s potential for sub-pixel landscape feature detection. Remote Sens. 2016, 8, 488. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in gaofen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef]











| Model | AICc | RSS | R2 | Adjusted R2 |
|---|---|---|---|---|
| GWR | −3087.201 | 85.8289 | 0.5144 | 0.4377 |
| OLS | −2220.059 | 132.1226 | 0.2524 | 0.2466 |
| Variables | F-Value | NDF | DDF | p-Value (Significance) | |
|---|---|---|---|---|---|
| F1-test | / | 0.75 | 3606.49 | 3966 | <2.20 × 10−16 *** |
| F3-test | Intercept | 6.85 | 348.37 | 3606.5 | <2.20×10−16 *** |
| NDVI_65 | 1.81 | 523.21 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_73 | 2.59 | 457.76 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_81 | 1.78 | 445.29 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_89 | 0.72 | 353.16 | 3606.5 | 0.999973 | |
| NDVI_97 | 4.75 | 332.68 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_105 | 2.08 | 258.34 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_113 | 3.61 | 269.81 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_121 | 1.15 | 484.77 | 3606.5 | 0.019104 * | |
| NDVI_129 | 1.02 | 485.38 | 3606.5 | 0.354737 | |
| NDVI_137 | 1.15 | 736.19 | 3606.5 | 0.006462 ** | |
| NDVI_145 | 1.32 | 589.97 | 3606.5 | 2.18 × 10−6 *** | |
| NDVI_153 | 0.53 | 666.26 | 3606.5 | 1 | |
| NDVI_161 | 0.86 | 907.46 | 3606.5 | 0.998103 | |
| NDVI_169 | 2.46 | 904.98 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_177 | 1.25 | 610.68 | 3606.5 | 8.12 × 10−5 *** | |
| NDVI_185 | 1.04 | 407.12 | 3606.5 | 0.296108 | |
| NDVI_193 | 1.40 | 629.78 | 3606.5 | 6.44 × 10−9 *** | |
| NDVI_201 | 0.85 | 292.13 | 3606.5 | 0.969006 | |
| NDVI_209 | 0.77 | 226.61 | 3606.5 | 0.995028 | |
| NDVI_217 | 1.64 | 252.09 | 3606.5 | 4.06 × 10−9 *** | |
| NDVI_225 | 4.43 | 160.93 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_233 | 7.19 | 227.22 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_241 | 13.18 | 336.43 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_249 | 2.70 | 632.45 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_257 | 11.21 | 711.35 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_265 | 2.93 | 772.44 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_273 | 3.30 | 955.55 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_281 | 2.40 | 737.06 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_289 | 2.13 | 622.15 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_297 | 1.80 | 418.44 | 3606.5 | <2.20 × 10−16 *** | |
| NDVI_305 | 1.55 | 634.59 | 3606.5 | 1.28 × 10−14 *** |
| Distance Calculation Ways | Bandwidth | AICc | RSS | R2 | Adjusted R2 |
|---|---|---|---|---|---|
| GCS/WGS84 (Great circle) | 736 | −3087.201 | 85.8289 | 0.5144 | 0.4377 |
| Sinusoidal (Euclidean distance) | 687 | −2928.25 | 88.4218 | 0.4997 | 0.4177 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Ma, Y.; Xu, B.; Song, Q.; Tang, H.; Wu, W. Estimating Sub-Pixel Soybean Fraction from Time-Series MODIS Data Using an Optimized Geographically Weighted Regression Model. Remote Sens. 2018, 10, 491. https://doi.org/10.3390/rs10040491
Hu Q, Ma Y, Xu B, Song Q, Tang H, Wu W. Estimating Sub-Pixel Soybean Fraction from Time-Series MODIS Data Using an Optimized Geographically Weighted Regression Model. Remote Sensing. 2018; 10(4):491. https://doi.org/10.3390/rs10040491
Chicago/Turabian StyleHu, Qiong, Yaxiong Ma, Baodong Xu, Qian Song, Huajun Tang, and Wenbin Wu. 2018. "Estimating Sub-Pixel Soybean Fraction from Time-Series MODIS Data Using an Optimized Geographically Weighted Regression Model" Remote Sensing 10, no. 4: 491. https://doi.org/10.3390/rs10040491
APA StyleHu, Q., Ma, Y., Xu, B., Song, Q., Tang, H., & Wu, W. (2018). Estimating Sub-Pixel Soybean Fraction from Time-Series MODIS Data Using an Optimized Geographically Weighted Regression Model. Remote Sensing, 10(4), 491. https://doi.org/10.3390/rs10040491