Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data
Abstract
:1. Introduction
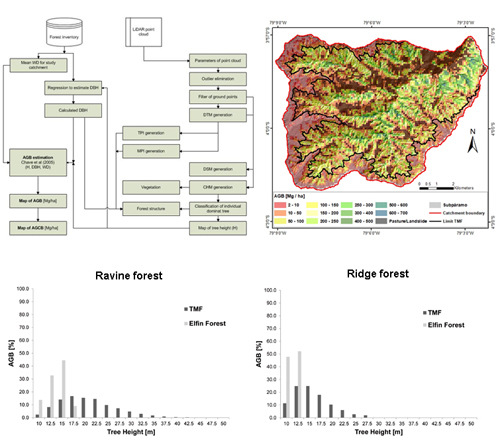
2. Materials and Methods
2.1. Study Area
2.2. LiDAR Data and Field Measurements
2.3. Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kou, W.; Liang, C.; Wei, L.; Hernandez, A.J.; Yang, X. Phenology-based method for mapping tropical evergreen forests by integrating of MODIS and Landsat imagery. Forests 2017, 8, 34. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Häger, A.; Schwendenmann, L. Forest Carbon Sequestration and Global Change. In The Paradigm of Forests and the Survival of the Fittest; Molina-Murillo, S.A., Rojas, C., Eds.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2016; pp. 39–86. ISBN 978-1-4987-5106-3. [Google Scholar]
- Ochoa-Cueva, P.; Fries, A.; Montesinos, P.; Rodríguez-Díaz, J.A.; Boll, J. Spatial Estimation of Soil Erosion Risk by Land-cover Change in the Andes of Southern Ecuador. Land Degrad. Dev. 2015, 26, 565–573. [Google Scholar] [CrossRef]
- UNFCCC. Fact Sheet: Reducing Emissions from Deforestation in Developing Countries: Approaches to Stimulate Action; FAO: Rome, Italy, 2011. [Google Scholar]
- Farmer, T.G. Modern Climate Change Science. An Overview of Today’s Climate Change Science; Springer: LasCruces, NM, USA, 2015; pp. 1–40. ISBN 978-3-319-09222-5. [Google Scholar]
- Spracklen, D.V.; Righelato, R. Carbon storage and sequestration of re-growing montane forests in southern Ecuador. For. Ecol. Manag. 2016, 364, 139–144. [Google Scholar] [CrossRef]
- González-Jaramillo, V.; Fries, A.; Rollenbeck, R.; Paladines, J.; Oñate-Valdivieso, F.; Bendix, J. Assessment of deforestation during the last decades in Ecuador using NOAA-AVHRR satellite data. Erdkunde 2016, 70, 217–235. [Google Scholar] [CrossRef]
- Franklin, J.; Serra-Diaz, J.M.; Syphard, A.D.; Regan, H.M. Global change and terrestrial plant community dynamics. Proc. Natl. Acad. Sci. USA 2016, 113, 3725–3734. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.; Bustamante, M.; Ahammad, H.; Clark, H.; Dong, H.; Elsiddig, E.A.; Haberl, H.; Harper, R.; House, J.; Jafari, M.; et al. Agriculture, Forestry and Other Land Use (AFOLU). In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; ISBN 978-1-107-65481-5. [Google Scholar]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Global Forest Resources Assessment 2015 Desk Reference; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Berenguer, E.; Ferreira, J.; Gardner, T.A.; Aragão, L.E.O.C.; De Camargo, P.B.; Cerri, C.E.; Durigan, M.; De Oliveira, R.C.; Vieira, I.C.G.; Barlow, J. A large-scale field assessment of carbon stocks in human-modified tropical forests. Glob. Chang. Biol. 2014, 20, 3713–3726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitchard, E.T.A.; Feldpausch, T.R.; Brienen, R.J.W.; Lopez-Gonzalez, G.; Monteagudo, A.; Baker, T.R.; Lewis, S.L.; Lloyd, J.; Quesada, C.A.; Gloor, M.; et al. Markedly divergent estimates of Amazon forest carbon density from ground plots and satellites. Glob. Ecol. Biogeogr. 2014, 23, 935–946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paulick, S.; Dislich, C.; Homeier, J.; Fischer, R.; Huth, A. The carbon fluxes in different successional stages: Modelling the dynamics of tropical montane forests in South Ecuador. For. Ecosyst. 2017, 4, 5. [Google Scholar] [CrossRef]
- Bhardwaj, D.R.; Banday, M.; Pala, N.A.; Rajput, B.S. Variation of biomass and carbon pool with NDVI and altitude in sub-tropical forests of northwestern Himalaya. Environ. Monit. Assess. 2016, 188, 635. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Muller-Landau, H.C.; Baker, T.R.; Easdale, T.A.; Steege, H.T.; Webb, C.O. Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecol. Appl. 2006, 16, 2356–2367. [Google Scholar] [CrossRef]
- Vieilledent, G.; Vaudry, R.; Andriamanohisoa, S.F.D.; Rakotonarivo, O.S.; Randrianasolo, H.Z.; Razafindrabe, H.N.; Rakotoarivony, C.B.; Ebeling, J.; Rasamoelina, M. A universal approach to estimate biomass and carbon stock in tropical forests using generic allometric models. Ecol. Appl. 2012, 22, 572–583. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Li, Z.; Yu, H.; Jiang, Z.; Wang, C.; Zhang, Y.; Qi, L.; Shi, L. Modeling of the height–diameter relationship using an allometric equation model: A case study of stands of Phyllostachys edulis. J. For. Res. 2016, 27, 339–347. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; Technical Report, FAO Forestry Paper 134; FAO: Rome, Italy, 1997. [Google Scholar]
- Ishihara, M.I.; Utsugi, H.; Tanouchi, H.; Aiba, M.; Kurokawa, H.; Onoda, Y.; Nagano, M.; Umehara, T.; Ando, M.; Miyata, R.; et al. Efficacy of generic allometric equations for estimating biomass: A test in Japanese natural forests. Ecol. Appl. 2015, 25, 1433–1446. [Google Scholar] [CrossRef] [PubMed]
- Leuschner, C.; Zach, A.; Moser, G.; Homeier, J.; Graefe, S.; Hertel, D.; Wittich, B.; Soethe, N.; Iost, S.; Röderstein, M.; et al. The Carbon Balance of Tropical Mountain Forests Along an Altitudinal Transect. In Ecosystem Services, Biodiversity and Environmental Change in a Tropical Mountain Ecosystem of South Ecuador, Ecological Studies; Bendix, J., Beck, E., Bräuning, A., Makeschin, F., Mosandl, R., Scheu, S., Wilcke, W., Eds.; Springer: Berlin, Germany, 2013; Volume 221, pp. 117–139. ISBN 978-3-642-38136-2. [Google Scholar]
- Werner, F.A.; Homeier, J. Is tropical montane forest heterogeneity promoted by a resource-driven feedback cycle? Evidence from nutrient relations, herbivory and litter decomposition along a topographical gradient. Funct. Ecol. 2015, 29, 430–440. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Jacquemoud, S.; Goncalves, G.; Silva, A.A.; Soares, P.; Tomé, M.; Pereira, L. Airbone Lidar Estimation of Aboveground Forest Biomass in the Absence of Field Inventory. Remote Sens. 2016, 8, 653. [Google Scholar] [CrossRef]
- Gourlet-Fleury, S.; Rossi, V.; Rejou-Mechain, M.; Freycon, V.; Fayolle, A.; Saint-André, L.; Cornu, G.; Gérard, J.; Sarrailh, J.M.; Flores, O.; et al. Environmental filtering of dense-wooded species controls above-ground biomass stored in African moist forests. J. Ecol. 2011, 99, 981–990. [Google Scholar] [CrossRef]
- Richter, M.; Moreira-Muñoz, A. Climatic heterogeneity and vegetation diversity in southern Ecuador investigated by phytoindication. Rev. Peru. Boil. 2005, 12, 217–238. [Google Scholar]
- Toivonen, J.M.; Gonzales-Inca, C.A.; Bader, M.Y.; Ruokolainen, K.; Kessler, M. Elevation Shifts in the Topographic Position of Polylepis Forest Stands in the Andes of Southern Peru. Forests 2018, 9, 7. [Google Scholar] [CrossRef]
- Kane, V.R.; Lutz, J.A.; Cansler, C.A.; Povak, N.A.; Churchill, D.J.; Smith, D.F.; Kane, J.T.; North, P. Water balance and topography predict fire and forest structure patterns. For. Ecol. Manag. 2015, 338, 1–13. [Google Scholar] [CrossRef]
- Paul, K.I.; Roxburgh, S.H.; Chave, J.; England, J.R.; Zerihun, A.; Specht, A.; Lewis, T.; Bennett, L.T.; Baker, T.G.; Adams, M.A.; et al. Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Glob. Chang. Biol. 2016, 22, 2106–2124. [Google Scholar] [CrossRef] [PubMed]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Tan, K.; Piao, S.; Peng, C.; Fang, J. Satellite-based estimation of biomass carbon stocks for northeast China’s forests between 1982 and 1999. For. Ecol. Manag. 2007, 240, 114–121. [Google Scholar] [CrossRef]
- Qin, Y.; Xiao, X.; Wang, J.; Dong, J.; Ewing, K.; Hoagland, B.; Hough, D.J.; Fagin, T.D.; Zou, Z.; Geissler, G.L.; et al. Mapping annual forest cover in sub-humid and semi-arid regions through analysis of Landsat and PALSAR imagery. Remote Sens. 2016, 8, 933. [Google Scholar] [CrossRef]
- Jochem, A.; Hollaus, M.; Rutzinger, M.; Höfle, B.; Schadauer, K.; Maier, B. Estimation of aboveground biomass using airborne LiDAR data. In Proceedings of the 10th International Conference on LiDAR Applications for Assessing Forest Ecosystems (Silvilaser 2010), Freiburg, Germany, 14–17 September 2010; p. 9. [Google Scholar]
- Kim, E.; Lee, W.-K.; Yoon, M.; Lee, J.-Y.; Son, Y.; Abu Salim, K. Estimation of Voxel-Based Above-Ground Biomass Using Airborne LiDAR Data in an Intact Tropical Rain Forest, Brunei. Forests 2016, 7, 259. [Google Scholar] [CrossRef]
- Bendix, J.; Rollenbeck, R.; Palacios, W.E. Cloud detection in the Tropics—A suitable tool for climate-ecological studies in the high mountains of Ecuador. Int. J. Remote Sens. 2004, 25, 4521–4540. [Google Scholar] [CrossRef]
- Posilero, M.A.V.; Paringit, E.C.; Argamosa, R.J.L.; Faelga, R.A.G.; Ibanez, C.A.G.; Zaragosa, G.P. Lidar—Based Canopy Cover Estimation Using Linear Regression Techniques. J. Philipp. Geosci. Remote Sens. Soc. 2016, 26–33. [Google Scholar]
- Li, A.; Dhakal, S.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Lidar aboveground vegetation biomass estimates in shrublands: Prediction, uncertainties and application to coarser scales. Remote Sens. 2017, 9, 903. [Google Scholar] [CrossRef]
- Stephens, P.R.; Kimberley, M.O.; Beets, P.N.; Paul, T.S.H.; Searles, N.; Bell, A.; Brack, C.; Broadley, J. Airborne scanning LiDAR in a double sampling forest carbon inventory. Remote Sens. Environ. 2012, 117, 348–357. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; She, G. Estimating forest structural parameters using canopy metrics derived from airborne LiDAR data in subtropical forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; version 3.70; United States Department of Agriculture, Forest Service: Washington, DC, USA, 2018.
- Piiroinen, R.; Heiskanen, J.; Maeda, E.; Viinikka, A.; Pellikka, P. Classification of tree species in a diverse African Agroforestry landscape using imaging spectroscopy and laser scanning. Remote Sens. 2017, 9, 875. [Google Scholar] [CrossRef]
- Ota, T.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; Ponce-Hernandez, R.; Ahmed, O.S.; et al. Estimating aboveground carbon using airborne LiDAR in Cambodian tropical seasonal forests for REDD+ implementation. J. For. Res. 2015, 20, 484–492. [Google Scholar] [CrossRef]
- Barnes, C.; Balzter, H.; Barrett, K.; Eddy, J.; Milner, S.; Suárez, J.C. Individual tree crown delineation from airborne laser scanning for diseased larch forest stands. Remote Sens. 2017, 9, 231. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.R.P.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.; et al. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Dubayah, R.O.; Cook, B.D.; Rosette, J.; Parker, G. The importance of spatial detail: Assessing the utility of individual crown information and scaling approaches for lidar-based biomass density estimation. Remote Sens. Environ. 2015, 168, 102–112. [Google Scholar] [CrossRef]
- Scaranello, M.A.S.; Alves, L.F.; Vieira, S.A.; Camargo, P.B.; Joly, C.A.; Martinelli, L.A. Height-diameter relationships of tropical Atlantic moist forest trees in Southeastern Brazil. Sci. Agric. 2012, 69, 26–37. [Google Scholar] [CrossRef]
- Slik, J.W.F.; Paoli, G.; McGuire, K.; Amaral, I.; Barroso, J.; Bastian, M.; Blanc, L.; Bongers, F.; Boundja, P.; Clark, C.; et al. Large trees drive forest aboveground biomass variation in moist lowland forests across the tropics. Glob. Ecol. Biogeogr. 2013, 22, 1261–1271. [Google Scholar] [CrossRef]
- Asner, G.P.; Clark, J.K.; Mascaro, J.; Vaudry, R.; Chadwick, K.D.; Vieilledent, G.; Rasamoelina, M.; Balaji, A.; Kennedy-Bowdoin, T.; Maatoug, L.; et al. Human and environmental controls over aboveground carbon storage in Madagascar. Carbon Balance Manag. 2012, 7, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, S.L.; Sonké, B.; Sunderland, T.; Begne, S.K.; Lopez-Gonzalez, G.; van der Heijden, G.M.F.; Phillips, O.L.; Affum-Baffoe, K.; Baker, T.R.; Banin, L.; et al. Above-ground biomass and structure of 260 African tropical forests. Philos. Trans. R. Soc. B 2013, 368, 1625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El Hajj, M.; Baghdadi, N.; Fayad, I.; Vieilledent, G.; Bailly, J.-S.; Minh, D.H.T. Interest of Integrating Spaceborne LiDAR Data to Improve the Estimation of Biomass in High Biomass Forested Areas. Remote Sens. 2017, 9, 213. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Quegan, S.; Toan, T.L.; Minh, D.H.T.; Saatchi, S.S.; Carvalhais, N.; Reichsteine, M.; Scipal, K. Coverage of high biomass forests by the ESA BIOMASS mission under defense restrictions. Remote Sens. Environ. 2017, 196, 154–162. [Google Scholar] [CrossRef]
- Leitold, V.; Keller, M.; Morton, D.C.; D Cook, B.; Shimabukuro, Y.E. Airborne lidar-based estimates of tropical forest structure in complex terrain: Opportunities and trade-offs for REDD+. Carbon Balance Manag. 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Anderson, C.B.; Martin, R.E.; Knapp, D.E.; Tupayachi, R.; Sinca, F.; Malhi, Y. Landscape-scale changes in forest structure and functional traits along an Andes-to-Amazon elevation gradient. Biogeosciences 2014, 11, 843–856. [Google Scholar] [CrossRef] [Green Version]
- Urbazaev, M.; Thiel, C.; Cremer, F.; Dubayah, R.; Migliavacca, M.; Reichstein, M.; Schmullius, C. Estimation of forest aboveground biomass and uncertainties by integration of field measurements, airborne LiDAR, and SAR and optical satellite data in Mexico. Carbon Balance Manag. 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Spracklen, D.V.; Righelato, R. Tropical montane forests are a larger than expected global carbon Store. Biogeosciences 2014, 11, 2741–2754. [Google Scholar] [CrossRef] [Green Version]
- Girardin, C.A.J.; Farfan-Rios, W.; Garcia, K.; Feeley, K.J.; Jørgensen, P.M.; Murakami, A.A.; Pérez, L.C.; Seidel, R.; Paniagua, N.; Claros, A.F.F.; et al. Spatial patterns of above-ground structure, biomass and composition in a network of six Andean elevation transects. Plant Ecol. Divers. 2014, 7, 161–171. [Google Scholar] [CrossRef]
- Mascaro, J.; Asner, G.P.; Muller-Landau, H.C.; van Breugel, M.; Hall, J.; Dahlin, K. Controls over aboveground forest carbon density on Barro Colorado Island, Panama. Biogeosciences 2011, 8, 1615–1629. [Google Scholar] [CrossRef] [Green Version]
- Raich, J.W.; Russell, A.E.; Kitayama, K.; Parton, W.J.; Vitousek, P.M. Temperature influences carbon accumulation in moist tropical forests. Ecology 2006, 87, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Unger, M.; Homeier, J.; Leuschner, C. Effects of soil chemistry on tropical forest biomass and productivity at different elevations in the equatorial Andes. Oecologia 2012, 170, 263–274. [Google Scholar] [CrossRef] [PubMed]
- Homeier, J.; Hertel, D.; Camenzind, T.; Cumbicus, N.L.; Maraun, M.; Martinson, G.O.; Poma, L.N.; Rillig, M.C.; Sandmann, D.; Scheu, S.; et al. Tropical Andean forests are highly susceptible to nutrient inputs—Rapid effects of experimental N and P addition to an Ecuadorian Montane Forest. PLoS ONE 2012, 7, e47128. [Google Scholar] [CrossRef] [PubMed]
- Fisher, J.B.; Malhi, Y.; Torres, I.C.; Metcalfe, D.B.; van de Weg, M.J.; Meir, P.; Silva-Especjo, J.E.; Huasco, W.H. Nutrient limitation in rainforests and cloud forests along a 3000 m elevation gradient in the Peruvian Andes. Oecologia 2013, 172, 889–902. [Google Scholar] [CrossRef] [PubMed]
- Leuschner, C.; Moser, G.; Bertsch, C.; Roderstein, M.; Hertel, D. Large altitudinal increase in tree root/shoot ratio in tropical mountain forests of Ecuador. Basic Appl. Ecol. 2007, 8, 219–230. [Google Scholar] [CrossRef]
- Riley, J.W.; Calhoun, D.L.; Barichivich, W.J.; Walls, S.C. Identifying Small Depressional Wetlands and Using a Topographic Position Index to Infer Hydroperiod Regimes for Pond-Breeding Amphibians. Wetlands 2017, 37, 325–338. [Google Scholar] [CrossRef]
- Richter, M.; Beck, E.; Rollenbeck, R.; Bendix, J. The Study Area. In Ecosystem Services, Biodiversity and Environmental Change in a Tropical Mountain Ecosystem of South Ecuador, Ecological Studies; Bendix, J., Beck, E., Bräuning, A., Makeschin, F., Mosandl, R., Scheu, S., Wilcke, W., Eds.; Springer: Berlin, Germany, 2013; Volume 221, pp. 1–19. ISBN 978-3-642-38136-2. [Google Scholar]
- Homeier, J.; Werner, F.A.; Gradstein, S.R.; Breckle, S.-W.; Richter, M. Potential vegetation and floristic composition of Andean forests in South Ecuador, with a focus on the RBSF. In Gradients in a Tropical Mountain Ecosystem of Ecuador; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 198, pp. 87–100. [Google Scholar]
- Bendix, J.; Beck, E. Spatial aspects of ecosystem research in a biodiversity hot spot of southern Ecuador—An introduction. Erdkunde 2009, 63, 305–308. [Google Scholar] [CrossRef]
- Beck, E.; Makeschin, F.; Haubrich, F.; Richter, M.; Bendix, J.; Valerezo, C. The Ecosystem (Reserva Biológica San Francisco). In Gradients in a Tropical Mountain Ecosystem of Ecuador; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 198, pp. 1–14. [Google Scholar]
- Curatola Fernández, G.F.; Obermeier, W.A.; Gerique, A.; López Sandoval, M.F.; Lehnert, L.W.; Thies, B.; Bendix, J. Land cover change in the Andes of southern Ecuador-Patterns and drivers. Remote Sens. 2015, 7, 2509–2542. [Google Scholar] [CrossRef]
- Moser, G.; Leuschner, C.; Hertel, D.; Graefe, S.; Soethe, N.; Iost, S. Elevation effects on the carbon budget of tropical mountain forests (S Ecuador): The role of the belowground compartment. Glob. Chang. Biol. 2011, 17, 2211–2226. [Google Scholar] [CrossRef]
- Dislich, C.; Huth, A. Modelling the impact of shallow landslides on forest structure in tropical montane forests. Ecol. Model. 2012, 239, 40–53. [Google Scholar] [CrossRef]
- Wagemann, J.; Thies, B.; Rollenbeck, R.; Peters, T.; Bendix, J. Regionalization of wind-speed data to analyze tree-line wind conditions in the eastern Andes of southern Ecuador. Erdkunde 2015, 69, 13–19. [Google Scholar] [CrossRef]
- Homeier, J.; Werner, F.A.; Gawlik, J.; Peters, T.; Diertl, K.H.J.; Richter, M. Plant Diversity and its Relevance for the Provision of Ecosystem Services. In Ecosystem Services, Biodiversity and Environmental Change in a Tropical Mountain Ecosystem of South Ecuador, Ecological Studies; Bendix, J., Beck, E., Bräuning, A., Makeschin, F., Mosandl, R., Scheu, S., Wilcke, W., Eds.; Springer: Berlin, Germany, 2013; Volume 221, pp. 100–118. ISBN 978-3-642-38136-2. [Google Scholar]
- Aguirre-Mendoza, Z.; Aguirre, N.; Merino, B.; Ochoa, I. Los páramos del Parque Nacional Podocarpus: Una aproximación a su diversidad ecosistémica y florística. In Cambio climático y Biodiversidad: Estudio de caso de los páramos del Parque Nacional Podocarpus; Aguirre, N., Ojeda, T., Eguiguren, E., Aguirre, Z., Eds.; Ediloja: Loja, Ecuador, 2015; pp. 22–45. [Google Scholar]
- Fries, A.; Rollenbeck, R.; Bayer, F.; Gonzalez, V.; Oñate-Valivieso, F.; Peters, T.; Bendix, J. Catchment precipitation processes in the San Francisco valley in southern Ecuador: Combined approach using high-resolution radar images and in situ observations. Meteorol. Atmos. Phys. 2014, 126, 13–29. [Google Scholar] [CrossRef]
- Roos, K.; Bendix, J.; Curatola, G.; Gawlik, J.; Gerique, A.; Hamer, U.; Hildebrandt, P.; Knoke, T.; Meyer, H.; Pohle, P.; et al. Current Provisioning Services: Pasture Development and Use, Weeds (Bracken) and Management. In Ecosystem Services, Biodiversity and Environmental Change in a Tropical Mountain Ecosystem of South Ecuador, Ecological Studies; Bendix, J., Beck, E., Bräuning, A., Makeschin, F., Mosandl, R., Scheu, S., Wilcke, W., Eds.; Springer: Berlin, Germany, 2013; Volume 221, pp. 230–243. ISBN 978-3-642-38136-2. [Google Scholar]
- Curatola Fernández, G.F.; Silva, B.; Gawlik, J.; Thies, B.; Bendix, J. Bracken fern frond status classification in the Andes of southern Ecuador: Combining multispectral satellite data and field spectroscopy. Int. J. Remote Sens. 2013, 34, 7020–7037. [Google Scholar] [CrossRef]
- Fries, A.; Rollenbeck, R.; Göttlicher, D.; Nauß, T.; Homeier, J.; Peters, T.; Bendix, J. Thermal structure of a megadiverse Andean mountain ecosystem in southern Ecuador and its regionalization. Erdkunde 2009, 63, 321–335. [Google Scholar] [CrossRef]
- Fries, A.; Rollenbeck, R.; Nauß, T.; Peters, T.; Bendix, J. Near surface air humidity in a megadiverse Andean mountain ecosystem of southern Ecuador and its regionalization. Agric. For. Meteorol. 2012, 152, 17–30. [Google Scholar] [CrossRef]
- Bendix, J.; Rollenbeck, R.; Richter, M.; Fabian, P.; Emck, P. Climate. In Gradients in a Tropical Mountain Ecosystem of Ecuador; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 198, pp. 63–74. [Google Scholar]
- Bendix, J.; Trachte, K.; Cermak, J.; Rollenbeck, R.; Nauß, T. Formation of Convective Clouds at the Foothills of the Tropical Eastern Andes (South Ecuador). J. Appl. Meteorol. Climatol. 2009, 48, 1682–1695. [Google Scholar] [CrossRef]
- Silva, B.; Bendix, J. Remote sensing of vegetation in a tropical mountain ecosystem: Individual tree-crown detection. Proc. SPIE 2013, 8893. [Google Scholar] [CrossRef]
- Homeier, J.; Breckle, S.-W.; Günter, S.; Rollenbeck, R.T.; Leuschner, C. Tree Diversity, Forest Structure and Productivity along Altitudinal and Topographical Gradients in a Species-Rich Ecuadorian Montane Rain Forest. Biotropica 2010, 42, 140–148. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Mildrexler, D.J.; Motesharrei, S.; Mu, Q.; Kalnay, E.; Zhao, F.; Li, S.; Wang, K. Potential and actual impacts of deforestation and afforestation on land surface temperature. J. Geophys. Res. 2016, 121, 14372–14386. [Google Scholar] [CrossRef]
- Gianico, V.; Lafortezza, R.; Jhon, R.; Sanesi, G.; Pesola, L.; Chen, J. Estimating Stand Volume and Above-Ground Biomass of Urban Forest Using LiDAR. Remote Sens. 2016, 8, 339. [Google Scholar] [CrossRef]
- Knoke, T.; Bendix, J.; Pohle, P.; Hamer, U.; Hildebrandt, P.; Roos, K.; Gerique, A.; Sandoval, M.L.; Breuer, L.; Tischer, A.; et al. Afforestation or intense pasturing improve the ecological and economic value of abandoned tropical farmlands. Nat. Commun. 2014, 5, 5612. [Google Scholar] [CrossRef] [PubMed]
- Eguiguren, P.; Aguirre, N.; Santín, A.; Vidal, E. Reservorios de carbono en los páramos del Parque Nacional Podocarpus. In Cambio Climático y Biodiversidad: Estudio de caso de los Páramos del Parque Nacional Podocarpus; Aguirre, N., Ojeda, T., Eguiguren, E., Aguirre, Z., Eds.; Ediloja: Loja, Ecuador, 2015; pp. 126–135. [Google Scholar]
- Levis, S.; Bonan, G.B.; Vertenstein, M.; Oleson, K.W. The Community Land Model’s Dynamic Global Model (CLM-DGVM): Technical Description and User’s Guide; National Center for Atmospheric Research: Boulder, CO, USA, 2004.
- Spriggs, R.; Coomes, D.; Jones, T.; Caspersen, J.; Vanderwel, M. An Alternative Approach to Using LiDAR Remote Sensing Data to Predict Stem Diameter Distributions across a Temperate Forest Landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef]
- Djomo, A.N.; Chimi, C.D. Tree allometric equations for estimation of above, below and total biomass in a tropical moist forest: Case study with application to remote sensing. For. Ecol. Manag. 2017, 391, 184–193. [Google Scholar] [CrossRef]
- Nogueira, E.M.; Nelson, B.W.; Fearnside, P.M.; França, M.B.; Oliveira, Á.C.A. de Tree height in Brazil’s “arc of deforestation”: Shorter trees in south and southwest Amazonia imply lower biomass. For. Ecol. Manag. 2008, 255, 2963–2972. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Barreiro-Fernández, L.; Buján, S.; Barbosa, M.; Suárez, J.C.; Bye, I.J.; Miranda, D. A mixed pixel- and region-based approach for using airborne laser scanning data for individual tree crown delineation in Pinus radiata D. Don plantations. Int. J. Remote Sens. 2013, 34, 7671–7690. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Airborne Light Detection and Ranging (LiDAR) for Individual Tree Stem Location, Height, and Biomass Measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef] [Green Version]
- Shiota, H.; Tanaka, K.; Nagashima, K. LiDAR Data Analysis with Fusion/LDV for Individual Tree. J. Biodivers. Manag. For. 2017, 2017, 6. [Google Scholar] [CrossRef]
- Molto, Q.; Hérault, B.; Boreux, J.J.; Daullet, M.; Rousteau, A.; Rossi, V. Predicting tree heights for biomass estimates in tropical forests—A test from French Guiana. Biogeosciences 2014, 11, 3121–3130. [Google Scholar] [CrossRef]
- SAGA GIS. System for Automated Geoscientific Analyses. Available online: http://www.saga-gis.org (accessed on 17 July 2017).
- Moran, N.; Nieland, S.; Suntrup, G.T.; Kleinschmit, B. Combining machine learning and onlotigal data handling for multi-source classification for nature conservation areas. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 124–133. [Google Scholar] [CrossRef]
- Weiss, A.D. Topographic position and landforms analysis. Presented at the ESRI User Conference, San Diego, CA, USA, 9–13 July 2001; Volume 64, pp. 227–245. Available online: http://www.jennessent.com/downloads/TPI-poster-TNC_18x22.pdf (accessed on 10 June 2017).
- Detto, M.; Muller-Landau, H.C.; Mascaro, J.; Asner, G.P. Hydrological Networks and Associated Topographic Variations as Templates for the Spatial Organization of Tropical Forest Vegetation. PLoS ONE 2013, 8, e76296. [Google Scholar] [CrossRef] [PubMed]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsas, O.M.; Malimbwi, R.E.; Naesset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forest of Tanzania. Carbon Balance Manag. 2015, 10, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bunning, S.; McDonagh, J.; Rioux, J. Land Degradation Assessment in Drylands. Manual for Local Level Assessment of Land Degradation and Sustainable Land Management. Part 1. Planning and Methodological Approach, Analysis and Reporting; FAO: Rome, Italy, 2011; p. 163. [Google Scholar]
- Kotowska, M.M.; Leuschner, C.; Triadiati, T.; Meriem, S.; Hertel, D. Quantifying above- and belowground biomass carbon loss with forest conversion in tropical lowlands of Sumatra (Indonesia). Glob. Chang. Biol. 2015, 21, 3620–3634. [Google Scholar] [CrossRef] [PubMed]
- Bastin, J.-F.; Barbier, N.; Réjou-Méchain, M.; Fayolle, A.; Gourlet-Fleury, S.; Maniatis, D.; de Haulleville, T.; Baya, F.; Beeckman, H.; Beina, D.; et al. Seeing Central African forests through their largest trees. Sci. Rep. 2015, 5, 13156. [Google Scholar] [CrossRef] [PubMed]
- Richter, M.; Diertl, K.H.; Peters, T.; Bussmann, R.W. Vegetation Structures and Ecological Features of the Upper Timberline Ecotone. In Gradients in a Tropical Mountain Ecosystem of Ecuador; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 198, pp. 123–146. [Google Scholar]
- Gibbon, A.; Silman, M.R.; Malhi, Y.; Fisher, J.B.; Meir, P.; Zimmermann, M.; Dargie, G.C.; Farfan, W.R.; Garcia, K.C. Ecosystem Carbon Storage Across the Grassland-Forest Transition in the High Andes of Manu National Park, Peru. Ecosystems 2010, 13, 1097–1111. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-Landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Banin, L.; Phillips, O.L.; Baker, T.R.; Lewis, S.L.; Quesada, C.A.; Affum-Baffoe, K.; Arets, E.J.M.M.; Berry, N.J.; Bird, M.; et al. Height-diameter allometry of tropical forest trees. Biogeosciences 2011, 8, 1081–1106. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.Z.A.; Bakar, M.A.A.; Razak, K.A.; Rasib, A.W.; Kanniah, K.D.; Kadir, W.H.W.; Omar, H.; Faidi, A.; Kassim, A.R.; Latif, Z.A. Non-destructive, laser-based individual tree aboveground biomass estimation in a tropical rainforest. Forests 2017, 8, 86. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus radiata D. Don plantations using different LiDAR pulse densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, Y.; Zhao, X.; von Gadow, K. Spatial Characteristics of Tree Diameter Distributions in a Temperate Old-Growth Forest. PLoS ONE 2013, 8, e58983. [Google Scholar] [CrossRef] [PubMed]
- Leuschner, C.; Moser, G. Carbon Allocation and productivity in tropical mountain forest. In The Tropical Mountain Forest. Patterns and Process in a Biodiversity Hotspot; Biodiversity and Ecology Series; Gradstein, S.R., Homeier, J., Gansert, D., Eds.; Universitätsverlang Göttingen: Göttingen, Germany, 2008; Volume 2, pp. 109–128. [Google Scholar]
- Dislich, C.; Günter, S.; Homeier, J.; Schröder, B.; Huth, A. Simulating forest dynamics of a tropical montane forest in South Ecuador. Erdkunde 2009, 63, 347–364. [Google Scholar] [CrossRef]
- Flores-López, F.; Galaitsi, S.E.; Escobar, M.; Purkey, D. Modeling of Andean páramo ecosystems’ hydrological response to environmental change. Water 2016, 8, 94. [Google Scholar] [CrossRef]
- MAE. Mecanismo REDD+ en Ecuador Introduce Material Informativo. Available online: http://www.ambiente.gob.ec/mecanismo-redd-en-ecuador-introduce-material-informativo/ (accessed on 5 May 2017).












| Parameter | Value |
|---|---|
| Scanning pattern | Sinusoid |
| Field Of View, deg | 0–75 |
| Pulse Rate (maximum), kHz | 150 |
| Pulse Wavelength, nm d | 1064 |
| Scan Rate (maximum), Hz | 90 |
| Number of returns | 4 |
| Forest Type | Tree Individuals | H [m] | DBH [cm] | AGB Tree [Mg] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TMF | 1,638,767 | Min | Mean | Max | Min | Mean | Max | Min | Mean | Max |
| Ravine | 1,470,493 | 8.5 | 13.3 | 48.4 | 10.0 | 23.5 | 223.3 | 0.0 | 0.3 | 47.1 |
| Ridge | 168,274 | 8.5 | 11.3 | 26.8 | 10.0 | 17.1 | 77.8 | 0.0 | 0.1 | 3.7 |
| Elfin Forest | 293,421 | Min | Mean | Max | Min | Mean | Max | Min | Mean | Max |
| Ravine | 271,717 | 8.5 | 11.0 | 15.7 | 10.0 | 16.4 | 30.1 | 0.0 | 0.1 | 0.4 |
| Ridge | 21,704 | 8.5 | 8.9 | 11.5 | 10.0 | 12.9 | 17.1 | 0.0 | 0.0 | 0.1 |
| AGB | C Stock | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [Mg ha−1] | [Mg ha−1] | ||||||||
| Forest Type | N [ha] | Min | Mean | Max | SD | Min | Mean | Max | SD |
| TMF * | 4608 | 10.0 | 106.2 | 664.1 | 94.1 | 5.0 | 53.1 | 332.0 | 47.0 |
| Elfin Forest | 1529 | 2.1 | 32.8 | 196.6 | 28.8 | 1.1 | 16.4 | 98.3 | 14.4 |
| Land Cover | Area [ha] | Area [%] | AGB [Mg] | C Stock [Mg C] | C Stock [%] |
|---|---|---|---|---|---|
| TMF | 4608 | 56.7 | 489,343.6 | 244,671.8 | 86.6 |
| Elfin Forest | 1529 | 18.8 | 50,117.2 | 25,058.6 | 8.9 |
| Pasture | 1200 | 14.8 | 12,960.0 | 6480.0 | 2.3 |
| Subpáramo | 785 | 9.7 | 12,874.0 | 6437.0 | 2.3 |
| TOTAL | 8122 | 100.0 | 565,294.8 | 282,647.4 | 100.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sens. 2018, 10, 660. https://doi.org/10.3390/rs10050660
González-Jaramillo V, Fries A, Zeilinger J, Homeier J, Paladines-Benitez J, Bendix J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sensing. 2018; 10(5):660. https://doi.org/10.3390/rs10050660
Chicago/Turabian StyleGonzález-Jaramillo, Víctor, Andreas Fries, Jörg Zeilinger, Jürgen Homeier, Jhoana Paladines-Benitez, and Jörg Bendix. 2018. "Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data" Remote Sensing 10, no. 5: 660. https://doi.org/10.3390/rs10050660
APA StyleGonzález-Jaramillo, V., Fries, A., Zeilinger, J., Homeier, J., Paladines-Benitez, J., & Bendix, J. (2018). Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sensing, 10(5), 660. https://doi.org/10.3390/rs10050660