Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data
Abstract
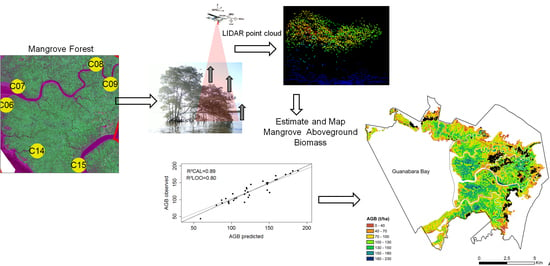
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Ground Data
2.3. Geolocation
2.4. Lidar Data
2.5. Lidar Processing
2.6. Biomass Models: Predicting Biomass on a Plot Level from Lidar Statistics
2.7. Mapping Biomass on a Landscape Level from Lidar Statistics
2.8. Sample Plot Coverage Assessment
2.9. Evaluating Uncertainty on the Landscape Level
3. Results
3.1. Landscape-Level Accuracy
3.1.1. Sample Coverage Assessment
3.1.2. Uncertainty at the Landscape Level
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. IPCC 2006 IPCC Guidelines for National Greenhouse Gas Inventories. In National Greenhouse Gas Inventories Programme; IGES: Tsukuba, Japan, 2006; p. 673. [Google Scholar]
- Meridian Institute. Reducing Emissions from Deforestation and Forest Degradation (REDD): An Options Assessment Report; Meridian Institute: Washington, DC, USA, 2009; Volume 6. [Google Scholar]
- Barbosa, J.M.; Broadbent, E.N.; Bitencourt, M.D. Remote Sensing of Aboveground Biomass in Tropical Secondary Forests: A Review. Int. J. For. Res. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Alongi, D.M. The Energetics of Mangrove Forests; Springer: Dordrecht, The Netherlands, 2009; ISBN 978-1-4020-4270-6. [Google Scholar]
- Webber, M.; Calumpong, H.; Ferreira, B.; Granek, E.; Green, S.; Ruwa, R.; Soares, M. Chapter 48. Mangroves. In UN World Ocean Assessmen; United Nations: New York, NY, USA, 2016; Available online: http://www.un.org/depts/los/global_reporting/WOA_RPROC/Chapter_48.pdf (accessed on 18 April 2018).
- Alongi, D.M. Carbon Cycling and Storage in Mangrove Forests. Annu. Rev. Mar. Sci 2014, 6, 195–219. [Google Scholar] [CrossRef] [PubMed]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Duke, N.C.; Meynecke, J.-O.; Dittmann, S.; Ellison, A.M.; Anger, K.; Berger, U.; Cannicci, S.; Diele, K.; Ewel, K.C.; Field, C.D.; et al. A World Without Mangroves? Science 2007, 317, 41–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Proisy, C.; Couteron, P.; Fromard, F.; Pélissier, R. Mangroves Dynamics from FOTO of IKONOS Images and Lidar Data. 2007. Available online: http://amapmed.free.fr/Ecolab_Fichiers/Contrib07/ProisyEcolabS2.pdf (accessed on 17 April 2018).
- Lucas, R.M.; Burting, P.; Clewley, D.; Proisy, C.; Souza-Filho, P.W.; Viergevr, K.; Woodhouse, L.; Ticehurst, C.; Carreiras, J.; Rosenqvist, A.; et al. Characterisation and Monitoring of Mangroves Using Alos Palsar Data; JAXA Earth Observation Research Center: Ibaraki, Japan, 2009; Available online: http://www.eorc.jaxa.jp/ALOS/en/kyoto/phase_1/KC-Phase1-report_Lucas_WT.pdf (accessed on 18 April 2018).
- Lucas, R.M.; Cronin, N.; Lee, A.; Moghaddam, M.; Witte, C.; Tickle, P. Empirical relationships between AIRSAR backscatter and LiDAR-derived forest biomass, Queensland, Australia. Remote Sens. Environ. 2006, 100, 407–425. [Google Scholar] [CrossRef]
- Simard, M.; Rivera-Monroy, V.H.; Mancera-pineda, J.E.; Castañeda-Moya, E.; Twilley, R.R. A systematic method for 3D mapping of mangrove forests based on Shuttle Radar Topography Mission elevation data, ICEsat/GLAS waveforms and field data: Application to Ciénaga Grande de Santa Marta, Colombia. Remote Sens. Environ. 2008, 112, 2131–2144. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Armstrong, A.H.; Space, G. Remote Characterization of Biomass Measurements: Case Study of Mangrove Forests. In Biomass; Momba, M., Bux, F., Eds.; SCIYO: Rijeka, Croatia, 2010; p. 202. ISBN 9789533071138. [Google Scholar]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Mascaro, J.; Asner, G.P.; Muller-Landau, H.C.; Van Breugel, M.; Hall, J.; Dahlin, K. Controls over aboveground forest carbon density on Barro Colorado Island, Panama. Biogeosciences 2011, 8, 1615–1629. [Google Scholar] [CrossRef] [Green Version]
- Vincent, G.; Sabatier, D.; Blanc, L.; Chave, J.; Weissenbacher, E.; Pélissier, R.; Fonty, E.; Molino, J.-F.; Couteron, P. Accuracy of small footprint airborne LiDAR in its predictions of tropical moist forest stand structure. Remote Sens. Environ. 2012, 125, 23–33. [Google Scholar] [CrossRef]
- Vincent, G.; Sabatier, D.; Rutishauser, E. Revisiting a universal airborne light detection and ranging approach for tropical forest carbon mapping: Scaling-up from tree to stand to landscape. Oecologia 2014, 175, 439–443. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Brolly, M.; Simard, M.; Tang, H.; Dubayah, R.O.; Fisk, J.P. A Lidar-Radar Framework to Assess the Impact of Vertical Forest Structure on Interferometric Coherence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5830–5841. [Google Scholar] [CrossRef]
- Clark, D.B.; Kellner, J.R. Tropical forest biomass estimation and the fallacy of misplaced concreteness. J. Veg. Sci. 2012, 23, 1191–1196. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Chen, Q.; Vaglio Laurin, G.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in LiDAR-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Næsset, E. Estimating above-ground biomass in young forests with airborne laser scanning. Int. J. Remote Sens. 2011, 32, 473–501. [Google Scholar] [CrossRef]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- D’Oliveira, M.V.N.; Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E. Estimating forest biomass and identifying low-intensity logging areas using airborne scanning lidar in Antimary State Forest, Acre State, Western Brazilian Amazon. Remote Sens. Environ. 2012, 124, 479–491. [Google Scholar] [CrossRef]
- Zhang, K. Identification of gaps in mangrove forests with airborne LIDAR. Remote Sens. Environ. 2008, 112, 2309–2325. [Google Scholar] [CrossRef]
- Hickey, S.M.; Callow, N.J.; Phinn, S.; Lovelock, C.E.; Duarte, C.M. Spatial complexities in aboveground carbon stocks of a semi-arid mangrove community: A remote sensing height-biomass-carbon approach. Estuar. Coast. Shelf Sci. 2018, 200, 194–201. [Google Scholar] [CrossRef]
- Chadwick, J. Integrated LiDAR and IKONOS multispectral imagery for mapping mangrove distribution and physical properties. Int. J. Remote Sens. 2011, 32, 6765–6781. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Simard, M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Object-Based Approach for Multi-Scale Mangrove Composition Mapping Using Multi-Resolution Image Datasets. Remote Sens. 2015, 7, 4753–4783. [Google Scholar] [CrossRef]
- Galvincio, J.D.; Popescu, S.C. Measuring Individual Tree Height and Crown Diameter for Mangrove Trees with Airborne Lidar Data. Int. J. Adv. Eng. Manag. Sci. 2016, 2, 431–443. [Google Scholar]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.; Feliciano, E.; Trettin, C.; Simard, M. A Comparison of Mangrove Canopy Height Using Multiple Independent Measurements from Land, Air, and Space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef] [PubMed]
- Wannasiri, W.; Nagai, M.; Honda, K.; Santitamnont, P.; Miphokasap, P. Extraction of Mangrove Biophysical Parameters Using Airborne LiDAR. Remote Sens. 2013, 5, 1787–1808. [Google Scholar] [CrossRef]
- Simard, M.; Zhang, K.; Rivera-Monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-moya, E.; Twilley, R.R.; Rodriguez, E. Mapping Height and Biomass of Mangrove Forests in Everglades National Park with SRTM Elevation Data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Trettin, C.C.; Stringer, C.E.; Zarnoch, S.J. Composition, biomass and structure of mangroves within the Zambezi River Delta. Wetl. Ecol. Manag. 2016, 24, 173–186. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Soares, M.L.G.; Schaeffer-Novelli, Y.; Gomes, M.; Schaeffer-Novelli, Y. Above-ground biomass of mangrove species. I. Analysis of models. Estuar. Coast. Shelf Sci. 2005, 65, 1–18. [Google Scholar] [CrossRef]
- Simard, M.; Fatoyinbo, L.E.; Pinto, N. Mangrove Canopy 3D Structure and Ecosystem Productivity Using Active Remote Sensing. 2009, pp. 61–78. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.549.842&rep=rep1&type=pdf (accessed on 18 April 2018).
- Arasato, L.S.; Bentz, C.M.; Fonseca, M.G.; Guerra, J.B.; Paes, J.E.S.; Freitas, L.R.; Costa, U.E.; Luiz, S. Avaliação do uso de modelos LiDAR e Worldview-1 para a caracterização e monitoramento de manguezais. In Anais XVII Simpósio Brasileiro de Sensoriamento Remoto; INPE: João Pessoa, Brasil, 2015; pp. 5050–5057. [Google Scholar]
- Fatoyinbo, T.L.; Feliciano, E.; Lagomasino, D.; Kuk Lee, S.; Trettin, C. Estimating mangrove aboveground biomass from airborne LiDAR data: A case study from the Zambezi River delta. Environ. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Pellens, R. (Org) Plano de Manejo da Área de Proteção Ambiental de Guapi-Mirim (APA de Guapi-Mirim); ICMBio: Brasilia, Brazil, 2001. [Google Scholar]
- INMET—Instituto Nacional de Meteorologia. Dados Meteorológico. Available online: http://www.inmet.gov.br/portal/index.php?r=bdmep/bdmep (accessed on 20 June 2016).
- Soares, M.L.G.; Chaves, F.D.O.; Moreira, F.; Milton, C. Diversidade Estrutural de Bosques de Mangue e sua Relação com Distúrbios de Origem Antrópica: O caso da Baía de Guanabara (Rio de Janeiro). Anu. Inst. Geociênc. UFRJ 2003, 26, 101–116. [Google Scholar] [CrossRef]
- Cavalcanti, V.F.; Soares, M.L.G.; Estrada, G.C.D.; Chaves, F.O. Evaluating Mangrove Conservation through the Analysis of Forest Structure Data. J. Coast. Res. 2009, 2009, 390–394. [Google Scholar]
- Schaeffer-Novelli, Y.; Cintrón-Molero, G. Guia Para Estudo de Áreas de Manguezal: Estrutura, Função e Flora; Caribbean Ecological Research: São Paulo, Brazil, 1986. [Google Scholar]
- Estrada, G.C.D.; Soares, M.L.G.; Santos, D.M.C.; Fernandez, V.; de Almeida, P.M.M.; de Estevam, M.R.M.; Machado, M.R.O. Allometric models for aboveground biomass estimation of the mangrove Avicennia schaueriana. Hydrobiologia 2014, 734, 171–185. [Google Scholar] [CrossRef]
- Estrada, G.C.D.; Soares, M.L.G.; Fernadez, V.; de Almeida, P.M.M. The economic evaluation of carbon storage and sequestration as ecosystem services of mangroves: A case study from southeastern Brazil. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2014, 11, 29–35. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Natural Resource Canada. GPS Positioning Guide; Natural Resource Canada: Ottawa, ON, Canada, 1995.
- Stephens, P.R.; Kimberley, M.O.; Beets, P.N.; Paul, T.S.H.; Searles, N.; Bell, A.; Brack, C.; Broadley, J. Airborne scanning LiDAR in a double sampling forest carbon inventory. Remote Sens. Environ. 2012, 117, 348–357. [Google Scholar] [CrossRef]
- Montesano, P.M.; Cook, B.D.; Sun, G.; Simard, M.; Nelson, R.F.; Ranson, K.J.; Zhang, Z.; Luthcke, S. Achieving accuracy requirements for forest biomass mapping: A spaceborne data fusion method for estimating forest biomass and LiDAR sampling error. Remote Sens. Environ. 2013, 130, 153–170. [Google Scholar] [CrossRef]
- Véga, C.; Renaud, J.P.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2016, 175, 32–42. [Google Scholar] [CrossRef]
- Chen, Q.; Qi, C. LiDAR Remote Sensing of Vegetation Biomass. Remote Sens. Nat. Resour. 2013, 399, 399–420. [Google Scholar] [CrossRef]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 3, 18–22. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. version 3.4.0. 2017. Available online: https://www.r-project.org/ (accessed on 17 April 2018).
- Schmidtlein, S.; Feilhauer, H.; Bruelheide, H. Mapping plant strategy types using remote sensing. J. Veg. Sci. 2012, 23, 395–405. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Mevik, B.-H.; Wehrens, R. The pls Package: Principle Component and Partial Least Squares Regression in R. J. Stat. Softw. 2007, 18, 1–24. [Google Scholar] [CrossRef]
- Piñeiro, G.; Perelman, S.; Guerschman, P.J.; Paruelo, M.J. How to Evaluate Models: Observed vs. Predicted or Predicted vs. Observed. Ecol. Modell. 2008, 316–322. [Google Scholar] [CrossRef]
- Arasato, L.S.; Bentz, C.M.; Silva, R.S.B.; Fonseca, M.G.; Guerra, J.B.; Paes, J.E.S.; Freitas, L.R.; Luiz, S. Uso do sensoriamento remoto ótico de alta resolução para a caracterização Manguezais, monitoramento qualitativo de manguezais. In Anais XVII Simpósio Brasileiro de Sensoriamento Remoto—SBSR; INPE: João Pessoa, Brasil, 2015; pp. 5141–5148. [Google Scholar]
- Fekety, P.A.; Falkowski, M.J.; Hudak, A.T. Temporal transferability of LiDAR-based imputation of forest inventory attributes. Can. J. For. Res. 2015, 435, 422–435. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Särdnal, C.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: Berlin/Heidelberg, Germany, 1992; pp. 1–694. [Google Scholar]
- Banskota, A.; Wynne, R.H.; Johnson, P.; Emessiene, B. Synergistic use of very high-frequency radar and discrete-return lidar for estimating biomass in temperate hardwood and mixed forests. Ann. For. Sci. 2011, 68, 347–356. [Google Scholar] [CrossRef]
- Hawbaker, T.J.; Keuler, N.S.; Lesak, A.A.; Gobakken, T.; Contrucci, K.; Radeloff, V.C. Improved estimates of forest vegetation structure and biomass with a LiDAR-optimized sampling design. J. Geophys. Res. Biogeosci. 2009, 114, 1–11. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.; Margolis, H.; Beaudoin, A.; Guindon, L.; Kimes, D. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Kennaway, T.A.; Helmer, E.H.; Lefsky, M.A.; Brandeis, T.A.; Sherrill, K.R. Mapping land cover and estimating forest structure using satellite imagery and coarse resolution lidar in the Virgin Islands. J. Appl. Remote Sens. 2008, 2, 27. [Google Scholar] [CrossRef]
- Asner, G.P.; Flint Hughes, R.; Varga, T.A.; Knapp, D.E.; Kennedy-Bowdoin, T. Environmental and biotic controls over aboveground biomass throughout a tropical rain forest. Ecosystems 2009, 12, 261–278. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Lim, K.S.; Treitz, P.M. Estimation of above ground forest biomass from airborne discrete return laser scanner data using canopy-based quantile estimators. Scand. J. For. Res. 2004, 19, 558–570. [Google Scholar] [CrossRef]
- Nelson, R.F.; Hyde, P.; Johnson, P.; Emessiene, B.; Imhoff, M.L.; Campbell, R.; Edwards, W. Investigating RaDAR-LiDAR synergy in a North Carolina pine forest. Remote Sens. Environ. 2007, 110, 98–108. [Google Scholar] [CrossRef]









| Equations | |||
|---|---|---|---|
| Species-Specific-AGB for Live Tree | |||
| A. schaueriana | Ln (AGB total) = 4.8017 + 2.5282 × Ln (DBH) | Estrada et al. (2014) | [54] |
| L. racemosa | Ln (AGB total) = 5.2394 + 2.2792 × Ln (DBH) | Soares et al. (2005) | [45] |
| R. mangle | Ln (AGB total) = 5.2985 + 2.4810 × Ln (DBH) | Soares et al. (2005) | [45] |
| Species-Specific-AGB for Dead Tree | |||
| A. schaueriana | Ln (AGB total) = 4.4117 + 2.5578 × Ln (DBH) | Estrada et al. (2014) | [54] |
| L. racemosa | Ln (AGB total) = 4.9308 + 2.2951 × Ln (DBH) | Soares et al. (2005) | [45] |
| R. mangle | Ln (AGB total) = 4.9851 + 2.5142 × Ln (DBH) | Soares et al. (2005) | [45] |
| Pantropical-AGB Total | |||
| AGB pantropical | AGB total = 251 × WD × (DBH 2.46) | Komiyama et al. (2008) | [44] |
| AGB pantropical | AGB total = 167.6 × WD × (DBH 2.47) | Chave et al. (2005) | [56] |
| Products | Main Specifications |
|---|---|
| Laser | Riegl LMS Q560 |
| Lidar point cloud | LAS format |
| Total surveyed area | 90 km2 |
| Geodesic reference system | WGS84 |
| Projection system | Universal Transverse Mercator (UTM) |
| Point density | 5 pulse m−2 (6 points m−2) |
| Altimetry precision | 15 cm |
| Planimetric accuracy | 50 cm |
| Swath angle | 60° (±30°) |
| Day and time of data acquisition Coordinated universal time (UTC) | 12 November 2012-17:20–19:02 UTC 12 December 2012-15:29–18:10 UTC |
| Tide height (tide gauge in GB) | 12 November 2012-17:20 UTC~0.86 m, 19:02 UTC~0.34 m 12 December 2012-15:29 UTC~0.89 m, 13:53 h~1.1 m, 18:10 UTC~0.9 m |
| Lidar Metrics | Lidar Metrics | ||
|---|---|---|---|
| Avg | Mean height | std | Standard deviation |
| d00 | Density points of 0.5–2 m | min | Minimum height |
| d01 | Density points of 2–4 m | p01 | Height percentile of 1% |
| d02 | Density points of 4–6 m | p05 | Height percentile of 5% |
| d03 | Density points of 6–8 m | p10 | Height percentile of 10% |
| d04 | Density points of 8–10 m | p25 | Height percentile of 25% |
| d05 | Density points of 10–12 m | p50 | Height percentile of 50% |
| d06 | Density points of 12–14 m | p75 | Height percentile of 75% |
| d07 | Density points of 14–16 m | p90 | Height percentile of 90% |
| d08 | Density points of 16–18 m | p95 | Height percentile of 95% |
| dns_gap | Density gap | p99 | Height percentile of 99% |
| kur | Kurtosis | qav | Quadratic mean |
| max | Maximum height | ske | Skewness |
| Model | Auto-PLS (a) | RF (b) | |
|---|---|---|---|
| M1sp species-specific | 34 plots (without buffer) | M1sp.autopls | M1sp.rf |
| M2sp species-specific | 34 plots with 5 m buffer (extended polygons) | M2sp.autopls | M2sp.rf |
| M3K pantropical_K | M3K.autopls | M3K.rf | |
| M4C pantropical_C | M4C.autopls | M4C.rf |
| Model | Auto-PLS (a) | Random Forest (b) |
|---|---|---|
| M1sp 34 plots without buffer species-specific | RMSE(CAL) = 14.70 RMSE(LOO) = 17.30 RMSE% =11.69% R2(CAL) = 0.80 R2(LOO) = 0.73 | RMSE = 18.60 RMSE% =14.79% R2 = 0.68 |
| M2sp 34 plots with 5-m buffer (extended polygons) species-specific | RMSE(CAL) = 11.17 RMSE(LOO) = 14.80 RMSE% = 8.88% R2(CAL) = 0.89 R2(LOO) = 0.80 | RMSE = 17.86 RMSE% = 14.20% R2 = 0.71 |
| M3K pantropical_K | RMSE(CAL) = 22.50 RMSE(LOO) = 24.90 RMSE% = 18.21% R2(CAL) = 0.39 R2(LOO) = 0.25 | RMSE = 25.99 RMSE% =21.04% R2 = 0.18 |
| M4C pantropical_C | RMSE(CAL) = 15.50 RMSE(LOO) = 17.10 RMSE% = 18.31% R2(CAL) = 0.39 R2(LOO) = 0.25 | RMSE = 17.60 RMSE% =20.79% R2 = 0.20 |
| Model | Landscape Mean (GREG) | Landscape SE (GREG) | Landscape Mean (Resampling) | Landscape SE (Resampling) |
|---|---|---|---|---|
| M2sp.autopls | 105.04 | 2.54 | 106.72 | 6.67 |
| M3K.autopls | 121.60 | 4.27 | 122.20 | 11.68 |
| M4C.autopls | 83.29 | 2.93 | 83.78 | 6.98 |
| Species | Map Area | Mean AGB M2sp.autopls | Mean AGB M3K.autopls | Mean AGB M4C.autopls | RMSD K | RMSD C | Mean Error K | Mean Error C |
|---|---|---|---|---|---|---|---|---|
| Av | 156,800 | 93.27 | 112.97 | 77.35 | 30.08 | 28.57 | 19.70 | -15.92 |
| Lg | 606,775 | 93.041 | 118.78 | 81.34 | 33.43 | 25.74 | 26.26 | -11.70 |
| Rh | 1026,500 | 125.13 | 127.94 | 87.67 | 23.75 | 44.408 | 2.81 | -37.47 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha de Souza Pereira, F.; Kampel, M.; Gomes Soares, M.L.; Estrada, G.C.D.; Bentz, C.; Vincent, G. Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data. Remote Sens. 2018, 10, 637. https://doi.org/10.3390/rs10040637
Rocha de Souza Pereira F, Kampel M, Gomes Soares ML, Estrada GCD, Bentz C, Vincent G. Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data. Remote Sensing. 2018; 10(4):637. https://doi.org/10.3390/rs10040637
Chicago/Turabian StyleRocha de Souza Pereira, Francisca, Milton Kampel, Mário Luiz Gomes Soares, Gustavo Calderucio Duque Estrada, Cristina Bentz, and Gregoire Vincent. 2018. "Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data" Remote Sensing 10, no. 4: 637. https://doi.org/10.3390/rs10040637
APA StyleRocha de Souza Pereira, F., Kampel, M., Gomes Soares, M. L., Estrada, G. C. D., Bentz, C., & Vincent, G. (2018). Reducing Uncertainty in Mapping of Mangrove Aboveground Biomass Using Airborne Discrete Return Lidar Data. Remote Sensing, 10(4), 637. https://doi.org/10.3390/rs10040637