Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions
Abstract
:1. Introduction
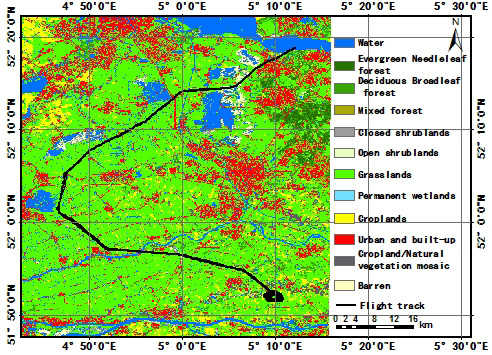
2. Study Area and Data Description
3. Methods
3.1. Data Preprocessing
3.2. Ogive Analysis
3.3. Uncertainty Estimation
3.4. Block Ensemble Averaging
4. Results
4.1. Ogive Analysis
4.1.1. Classification of Ogive Curves
4.1.2. Determination of Possible Window Length
4.2. Uncertainty Associated with the Window Length
4.3. Evaluation of the Optimizing Window Length
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chen, J.M.; Leblanc, S.G.; Cihlar, J. Extending aircraft- and tower-based CO2 flux measurements to a boreal region using a landsat thematic mapper land cover map. J. Geophys. Res. Atmos. 1999, 104, 16859–16877. [Google Scholar] [CrossRef]
- Desjardins, R.L.; MacPherson, J.I.; Mahrt, L.; Schuepp, P.; Pattey, E.; Neumann, H.; Baldocchi, D.; Wofsy, S.; Fitzjarrald, D.; McCaughey, H.; et al. Scaling up flux measurements for the boreal forest using aircraft-tower combinations. J. Geophys. Res. Atmos. 1997, 102, 29125–29133. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J.C. Footprint estimation for scalar flux measurements in the atmospheric surface layer. Bound.-Layer Meteorol. 1992, 59, 279–296. [Google Scholar] [CrossRef]
- Saac, P.R.; McAneney, J.; Leuning, R.; Hacker, J.M. Comparison of aircraft and ground-based flux measurements during Oasis95. Bound.-Layer Meteorol. 2004, 110, 39–67. [Google Scholar]
- Bertoldi, G.; Kustas, W.P.; Albertson, J.D. Evaluating source area contributions from aircraft flux measurements over heterogeneous land using large-eddy simulation. Bound.-Layer Meteorol. 2013, 147, 261–279. [Google Scholar] [CrossRef]
- Metzger, S.; Junkermann, W.; Mauder, M.; Butterbach-Bahl, K.; Widemann, B.T.; Neidl, F.; Schafer, K.; Wieneke, S.; Zheng, X.H.; Schmid, H.P.; et al. Spatially explicit regionalization of airborne flux measurements using environmental response functions. Biogeosciences 2013, 10, 2193–2217. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.D.; Hincks, B.B.; Meyers, T.P. Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Foken, T.; Aubinet, M.; Leuning, R. The eddy covariance method. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Aubinet, M., Vesala, T., Papale, D., Eds.; Springer Netherlands: Dordrecht, The Nederlands, 2012; pp. 1–19. [Google Scholar]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H.A. A re-evaluation of long-term flux measurement techniques—Part I: Averaging and coordinate rotation. Bound.-Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Lee, X.; Massman, W.; Law, B. Handbook of Micrometeorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 7–238. [Google Scholar]
- Foken, T.; Wimmer, F.; Mauder, M.; Thomas, C.; Liebethal, C. Some aspects of the energy balance closure problem. Atmos. Chem. Phys. 2006, 6, 4395–4402. [Google Scholar] [CrossRef]
- Mahrt, L.; Macpherson, J.I.; Desjardins, R. Observations of fluxes over heterogeneous surfaces. Bound.-Layer Meteorol. 1994, 67, 345–367. [Google Scholar] [CrossRef]
- Mitic, C.M.; Schuepp, P.H.; Desjardins, R.L.; Macpherson, I.J. Flux association in coherent structures transporting CO2, H2O, heat and ozone over the code grid site. Agric. For. Meteorol. 1997, 87, 27–39. [Google Scholar] [CrossRef]
- Aubinet, M. Eddy covariance CO2 flux measurements in nocturnal conditions: An analysis of the problem. Ecol. Appl. 2008, 18, 1368–1378. [Google Scholar] [CrossRef] [PubMed]
- Von Randow, C.; Sa, L.D.A.; Gannabathula, P.; Manzi, A.O.; Arlino, P.R.A.; Kruijt, B. Scale variability of atmospheric surface layer fluxes of energy and carbon over a tropical rain forest in southwest amazonia-1. Diurnal conditions. J. Geophys. Res.-Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Sievers, J.; Papakyriakou, T.; Larsen, S.E.; Jammet, M.M.; Rysgaard, S.; Sejr, M.K.; Sørensen, L.L. Estimating surface fluxes using eddy covariance and numerical ogive optimization. Atmos. Chem. Phys. 2015, 15, 2081–2103. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.M.; Zhu, Z.L.; Wen, X.F.; Yuan, G.F.; Yu, G.R. The impact of averaging period on eddy fluxes observed at chinaflux sites. Agric. For. Meteorol. 2006, 137, 188–193. [Google Scholar] [CrossRef]
- Lenschow, D.H.; Mann, J.; Kristensen, L. How long is long enough when measuring fluxes and other turbulence statistics. J. Atmos. Ocean. Technol. 1994, 11, 661–673. [Google Scholar] [CrossRef]
- Lemone, M.A.; Grossman, R.L.; Chen, F.; Lkeda, K.; Yates, D.N. Choosing the averaging interval for comparison of observed and modeled fluxes along aircraft transects over a heterogeneous surface. J. Hydrometeorol. 2003, 2, 179–195. [Google Scholar] [CrossRef]
- Lenschow, D.H.; Stankov, B.B. Length scales in the convective boundary layer. J. Atmos. Sci. 1986, 43, 1198–1209. [Google Scholar] [CrossRef]
- Mauder, M.; Desjardins, R.L.; MacPherson, I. Scale analysis of airborne flux measurements over heterogeneous terrain in a boreal ecosystem. J. Geophys. Res. 2007, D13112, 1–13. [Google Scholar] [CrossRef]
- Charuchittipan, D.; Babel, W.; Mauder, M.; Leps, J.-P.; Foken, T. Extension of the averaging time in eddy-covariance measurements and its effect on the energy balance closure. Bound.-Layer Meteorol. 2014, 152, 303–327. [Google Scholar] [CrossRef]
- Grossman, R.L. Sampling errors in the vertical fluxes of potential temperature and moisturemeasured by aircraft during fife. J. Geophys. Res. 1992, 97, 18439–18443. [Google Scholar] [CrossRef]
- Crawford, T.L.; McMillen, R.T.; Dobosy, R.J.; Macpherson, I. Correcting airborne flux measurements for aircraft speed variation. Bound.-Layer Meteorol. 1993, 66, 237–245. [Google Scholar] [CrossRef]
- Mauder, M.; Desjardins, R.L.; MacPherson, I. Creating surface flux maps from airborne measurements: Application to the Mackenzie area Gewex study Mags 1999. Bound.-Layer Meteorol. 2008, 129, 431–450. [Google Scholar] [CrossRef]
- Kirby, S.; Dobosy, R.; Williamson, D.; Dumas, E. An aircraft-based data analysis method for discerning individual fluxes in a heterogeneous agricultural landscape. Agric. For. Meteorol. 2008, 148, 481–489. [Google Scholar] [CrossRef]
- Beyrich, F.; Leps, J.P.; Mauder, M.; Bange, J.; Foken, T.; Huneke, S.; Lohse, H.; Lüdi, A.; Meijninger, W.M.L.; Mironov, D. Area-averaged surface fluxes over the litfass region based on eddy-covariance measurements. Bound.-Layer Meteorol. 2006, 121, 33–65. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar]
- Mahrt, L. Computing turbulent fluxes near the surface: Needed improvements. Agric. For. Meteorol. 2010, 150, 501–509. [Google Scholar] [CrossRef]
- Gioli, B.; Miglietta, F.; Vaccari, F.P.; Zaldei, A.; Martino, B.D. The sky arrow era, an innovative airborne platform to monitor mass, momentum and energy exchange of ecosystems. Ann. Geophys. 2006, 49, 109–116. [Google Scholar]
- Michels, B.I.; Jochum, A.M. Heat and moisture flux profiles in a region with inhomogeneous surface evaporation. J. Hydrol. 1995, 166, 383–407. [Google Scholar] [CrossRef]
- Brasa-Ramos, A.; de Santa Olalla, F.M.I.; Caselles, V.; Jochum, A.M. Comparison of evapotranspiration estimates by noaa-avhrr images and aircraft flux measurements in a semiarid region of Spain. J. Agric. Eng. Res. 1998, 70, 285–294. [Google Scholar] [CrossRef]
- Bange, J.; Zittel, P.; Spieß, T.; Uhlenbrock, J.; Beyrich, F. A new method for the determination of area-averaged turbulent surface fluxes from low-level flights using inverse models. Bound.-Layer Meteorol. 2006, 119, 527–561. [Google Scholar] [CrossRef]
- Friehe, C.A.; Shaw, W.J.; Rogers, D.P.; Davidson, K.L.; Large, W.G.; Stage, S.A.; Crescenti, G.H.; Khalsa, S.J.S.; Greenhut, G.K.; Li, F. Air-sea fluxes and surface layer turbulence around a sea surface temperature front. J. Geophys. Res. Oceans 1991, 96, 8593–8609. [Google Scholar] [CrossRef]
- Bange, J.; Beyrich, F.; Engelbart, D.A.M. Airborne measurements of turbulent fluxes during litfass-98: Comparison with ground measurements and remote sensing in a case study. Theor. Appl. Climatol. 2002, 73, 35–51. [Google Scholar] [CrossRef]
- Foken, T. Experimental methods for estimating the fluxes of energy and matter. In Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 105–151. [Google Scholar]
- Desjardins, R.L.; MacPherson, J.I.; Schuepp, P.H.; Karanja, F. An evaluation of aircraft flux measurements of CO2, water vapor and sensible heat. Bound.-Layer Meteorol. 1989, 47, 55–69. [Google Scholar] [CrossRef]
- Gioli, B.; Miglietta, F.; De Martino, B.; Hutjes, R.W.A.; Dolman, H.A.J.; Lindroth, A.; Schumacher, M.; Sanz, M.J.; Manca, G.; Peressotti, A.; et al. Comparison between tower and aircraft-based eddy covariance fluxes in five european regions. Agric. For. Meteorol. 2004, 127, 1–16. [Google Scholar] [CrossRef]
- Hutjes, R.W.A.; Vellinga, U.S.; Gioli, B.; Miglietta, F. Dis-aggregation of airborne flux measurements using footprint analysis. Agric. For. Meteorol. 2010, 150, 966–983. [Google Scholar] [CrossRef]
- Ogunjemiyo, S.O.; Kaharabata, S.K.; Schuepp, P.H.; MacPherson, I.J.; Desjardins, R.L.; Roberts, D.A. Methods of estimating CO2, latent heat and sensible heat fluxes from estimates of land cover fractions in the flux footprint. Agric. For. Meteorol. 2003, 117, 125–144. [Google Scholar] [CrossRef]
- Vellinga, O.S.; Dobosy, R.J.; Dumas, E.J.; Gioli, B.; Elbers, J.A.; Hutjes, R.W.A. Calibration and quality assurance of flux observations from a small research aircraft. J. Atmos. Ocean. Technol. 2013, 30, 161–181. [Google Scholar] [CrossRef]
- Miglietta, F.; Gioli, B.; Brunet, Y.; Hutjes, R.W.A.; Matese, A.; Sarrat, C.; Zaldei, A. Sensible and latent heat flux from radiometric surface temperatures at the regional scale: Methodology and evaluation. Biogeosciences 2009, 6, 1975–1986. [Google Scholar] [CrossRef]
- Vellinga, O.S.; Gioli, B.; Elbers, J.A.; Holtslag, A.A.M.; Kabat, P.; Hutjes, R.W.A. Regional carbon dioxide and energy fluxes from airborne observations using flight-path segmentation based on landscape characteristics. Biogeosciences 2010, 7, 1307–1321. [Google Scholar] [CrossRef]
- Isaac, P.R.; Leuning, R.; Hacker, J.M.; Cleugh, H.A.; Coppin, P.A.; Denmead, O.T.; Raupach, M.R. Estimation of regional evapotranspiration by combining aircraft and ground-based measurements. Bound.-Layer Meteorol. 2004, 110, 69–98. [Google Scholar] [CrossRef]
- Lothon, M.; Couvreux, F.; Donier, S.; Guichard, F.; Lacarrère, P.; Lenschow, D.H.; Noilhan, J.; Saïd, F. Impact of coherent eddies on airborne measurements of vertical turbulent fluxes. Bound.-Layer Meteorol. 2007, 124, 425–447. [Google Scholar] [CrossRef]
- Caramori, P.; Schuepp, P.H.; Desjardins, R.L.; Macpherson, J.I. Structural analysis of airborne flux estimates over a region. J. Clim. 1994, 7, 627–640. [Google Scholar] [CrossRef]
- Lemone, M.A.; Grossman, R.L.; McMillen, R.T.; Liou, K.-N.; Ou, S.C.; McKeen, S.; Angevine, W.; Ikeda, K.; Chen, F. Cases-97: Late-morning warming and moistening of the convective boundary layer over the walnut river watershed. Bound.-Layer Meteorol. 2002, 104, 1–52. [Google Scholar] [CrossRef]
- Hutjes, R.; Vellinga, O.; Elbers, J. Using aircraft observations to characterise the full seasonal dynamics of evaporation and carbon dioxide fluxes from heterogeneous landscapes in The Netherlands. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 7–12 April 2013; Volume 15. [Google Scholar]
- Meesters, A.; Tolk, L.F.; Peters, W.; Hutjes, R.W.A.; Vellinga, O.S.; Elbers, J.A.; Vermeulen, A.T.; van der Laan, S.; Neubert, R.E.M.; Meijer, H.A.J.; et al. Inverse carbon dioxide flux estimates for The Netherlands. J. Geophys. Res.-Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Hacker, J.; Crawford, T. The bat-probe: The ultimate tool to measure turbulence from any kind of aircraft (or sailplane). Tech. Soar. 1999, 2, 42–45. [Google Scholar]
- Dumas, E.J.; Brooks, S.B.; Verfaillie, J. Development and testing of a sky arrow 650 era for atmospheric research. In Proceedings of the 11th Symposium on Meteorological Observations and Instrumentation, Albuquerque, NM, USA, 14–18 January 2001; pp. 129–133. [Google Scholar]
- Hazeu, G.W.; Bregt, A.K.; de Wit, A.J.W.; Clevers, J. A Dutch multi-date land use database: Identification of real and methodological changes. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 682–689. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J. Scale issues in boundary-layer meteorology-surface-energy balances in heterogeneous terrain. Hydrol. Process. 1995, 9, 589–612. [Google Scholar] [CrossRef]
- Grunwald, J.; Kalthoff, N.; Corsmeier, U.; Fiedler, E. Comparison of areally averaged turbulent fluxes over non-homogeneous terrain: Results from the efeda-field experiment. Bound.-Layer Meteorol. 1996, 77, 105–134. [Google Scholar] [CrossRef]
- Foken, T. 50 years of the monin–obukhov similarity theory. Bound.-Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Clifford, S.F.; Lataitis, R.J. Effect of finite sampling on atmospheric spectra. Bound.-Layer Meteorol. 1989, 47, 337–347. [Google Scholar] [CrossRef]
- Lenschow, D.H.; Sun, J.L. The spectral composition of fluxes and variances over land and sea out to the mesoscale. Bound.-Layer Meteorol. 2007, 125, 63–84. [Google Scholar] [CrossRef]
- Stull, R.B. Some mathematical & conceptual tools: Part 1. Statistics. In An Introduction to Boundary Layer Meteorology; Stull, R.B., Ed.; Springer: Dordrecht, The Nederlands, 1988; pp. 29–74. [Google Scholar]
- Berger, B.W.; Davis, K.J.; Yi, C.X.; Bakwin, P.S.; Zhao, C.L. Long-term carbon dioxide fluxes from a very tall tower in a northern forest: Flux measurement methodology. J. Atmos. Ocean. Technol. 2001, 18, 529–542. [Google Scholar] [CrossRef]
- Mauder, M.; Cuntz, M.; Drue, C.; Graf, A.; Rebmann, C.; Schmid, H.P.; Schmidt, M.; Steinbrecher, R. A strategy for quality and uncertainty assessment of long-term eddy-covariance measurements. Agric. For. Meteorol. 2013, 169, 122–135. [Google Scholar] [CrossRef]
- Mahrt, L. Flux sampling errors for aircraft and towers. J. Atmos. Ocean. Technol. 1998, 15, 416–429. [Google Scholar] [CrossRef]
- Betts, A.K.; Desjardins, R.L.; Macpherson, J.I.; Kelly, R.D. Boundary-layer heat and moisture budgets from fife. Bound.-Layer Meteorol. 1990, 50, 109–138. [Google Scholar] [CrossRef]
- Lemone, M.A.; Chen, F.; Alfieri, J.G.; Tewari, M.; Geerts, B.; Miao, Q.; Grossman, R.L.; Coulter, R.L. Influence of land cover and soil moisture on the horizontal distribution of sensible and latent heat fluxes in southeast kansas during ihop_2002 and cases-97. J. Hydrometeorol. 2006, 8, 68–87. [Google Scholar] [CrossRef]
- Billesbach, D.P. Estimating uncertainties in individual eddy covariance flux measurements: A comparison of methods and a proposed new method. Agric. For. Meteorol. 2011, 151, 394–405. [Google Scholar] [CrossRef]
- Finkelstein, P.L.; Sims, P.F. Sampling error in eddy correlation flux measurements. J. Geophys. Res.-Atmos. 2001, 106, 3503–3509. [Google Scholar] [CrossRef]
- Sun, J.L.; Howell, J.F.; Esbensen, S.K.; Mahrt, L.; Greb, C.M.; Grossman, R.; LeMone, M.A. Scale dependence of air-sea fluxes over the western equatorial pacific. J. Atmos. Sci. 1996, 53, 2997–3012. [Google Scholar] [CrossRef]
- Sakai, R.K.; Fitzjarrald, D.R.; Moore, K.E. Importance of low-frequency contributions to eddy fluxes observed over rough surfaces. J. Appl. Meteorol. 2001, 40, 2178–2192. [Google Scholar] [CrossRef]
- Albertson, J.D.; Parlange, M.B. Natural integration of scalar fluxes from complex terrain. Adv. Water Resour. 1999, 23, 239–252. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; French, A.N.; Vickers, D. Using a remote sensing field experiment to investigate flux-footprint relations and flux sampling distributions for tower and aircraft-based observations. Adv. Water Resour. 2006, 29, 355–368. [Google Scholar] [CrossRef]
- Mahrt, L.; Vickers, D.; Sun, J.L. Spatial variations of surface moisture flux from aircraft data. Adv. Water Resour. 2001, 24, 1133–1141. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Olesen, H.R.; Larsen, S.E.; Hojstrup, J. Modeling velocity spectra in the lower part of the planetary boundary-layer. Bound.-Layer Meteorol. 1984, 29, 285–312. [Google Scholar] [CrossRef]
- Hojstrup, J. Velocity spectra in the unstable planetary boundary-layer. J. Atmos. Sci. 1982, 39, 2239–2248. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Van den Kroonenberg, A.; Bange, J. Turbulent flux calculation in the polar stable boundary layer: Multiresolution flux decomposition and wavelet analysis. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Cheng, W.C.; Liu, C.H. Large-eddy simulation of turbulent transports in urban street canyons in different thermal stabilities. J. Wind Eng. Ind. Aerodyn. 2011, 99, 434–442. [Google Scholar] [CrossRef]
- Bertoldi, G.; Kustas, W.P.; Albertson, J.D. Estimating spatial variability in atmospheric properties over remotely sensed land surface conditions. J. Appl. Meteorol. Climatol. 2008, 47, 2147–2165. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. The cospectral gap and turbulent flux calculations. J. Atmos. Ocean. Technol. 2003, 20, 660–672. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; RG, L. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]











| Date | Time (UTC) | Altitude (m) | M–O Stability () |
|---|---|---|---|
| 29 February 2008 | 13:03–13:53 | 57 | −0.04 |
| 11 April 2008 | 11:14–11:47 | 67 | −10.03 |
| 11 April 2008 | 12:29–13:03 | 65 | −10.27 |
| 2 May 2008 | 10:58–11:30 | 71 | −1.08 |
| 2 May 2008 | 11:53–12:25 | 78 | −0.63 |
| 23 May 2008 | 08:32–09:05 | 68 | −2.24 |
| 23 May 2008 | 09:41–10:14 | 69 | −3.82 |
| 13 June 2008 | 10:19–10:50 | 76 | −0.32 |
| 13 June 2008 | 11:07–11:40 | 71 | −0.47 |
| 4 July 2008 | 11:32–12:05 | 66 | 0.05 |
| 4 July 2008 | 12:32–13:08 | 66 | 0.01 |
| 25 July 2008 | 09:52–10:23 | 66 | −0.34 |
| 25 July 2008 | 10:51–11:20 | 68 | −0.35 |
| 15 August 2008 | 10:25–11:01 | 66 | −0.22 |
| 15 August 2008 | 11:30–12:06 | 66 | −0.36 |
| 5 September 2008 | 09:10–09:39 | 63 | −0.12 |
| 17 October 2008 | 13:27–13:59 | 73 | −0.26 |
| 31 October 2008 | 13:08–13:39 | 69 | −0.43 |
| 11 December 2008 | 13:48–14:24 | 74 | 0.02 |
| Case | Explanation | Criterion |
|---|---|---|
| (1) Convergent | Convergent within the 2 km interval. Ideal case. | and |
| (2) Divergent | Ogive curve is not convergent within 2 km interval, but is convergent in the wavelength larger than 2 km. Window length should be longer. | and |
| (3) Inadequate | Ogive curve is not convergent even for 10 km interval. Unclear cospectral gap. | and and |
| (4) Sign Reversal | Ogive curve undergoes a relatively large sign reversal in low-wavenumber domain while maintaining the normal Ogive shape. | and |
| (5) Shape Reversal | Ogive curve undergoes a very large sign reversal and displays reversed shape compared with other cases. | and |
| Ogive Case () | Neutral (%) | Moderately Unstable (%) | Very Unstable (%) | All Stabilities (%) |
|---|---|---|---|---|
| Case 1: Convergent | 11.6 | 15.2 | 23.8 | 15.5 |
| Case 2: Divergent | 7 | 34.8 | 38.1 | 24.5 |
| Case 3: Inadequate | 16.3 | 21.7 | 23.8 | 20 |
| Case 4 and Case 5: Reversed | 62.8 | 26.1 | 9.5 | 37.3 |
| Ogive Case () | Neutral (%) | Moderately Unstable (%) | Very Unstable (%) | All Stabilities (%) |
|---|---|---|---|---|
| Case 1: Convergent | 27.9 | 15.2 | 18.2 | 20.7 |
| Case 2: Divergent | 20.9 | 43.5 | 59.1 | 37.9 |
| Case 3: Inadequate | 11.7 | 19.6 | 4.5 | 13.5 |
| Case 4 and Case 5: Reversed | 39.5 | 21.7 | 18.2 | 27.9 |
| Atmospheric Stability Condition () | Optimum Window Length (m) |
|---|---|
| neutral conditions () | 2000–2500 |
| moderately unstable conditions () | 3900–5000 |
| Very unstable conditions () | 4500–5000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Jia, L.; Chen, Q.; Zheng, C. Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions. Remote Sens. 2018, 10, 670. https://doi.org/10.3390/rs10050670
Sun Y, Jia L, Chen Q, Zheng C. Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions. Remote Sensing. 2018; 10(5):670. https://doi.org/10.3390/rs10050670
Chicago/Turabian StyleSun, Yibo, Li Jia, Qiting Chen, and Chaolei Zheng. 2018. "Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions" Remote Sensing 10, no. 5: 670. https://doi.org/10.3390/rs10050670
APA StyleSun, Y., Jia, L., Chen, Q., & Zheng, C. (2018). Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions. Remote Sensing, 10(5), 670. https://doi.org/10.3390/rs10050670