Next Article in Journal
Monitoring Surface Deformation over a Failing Rock Slope with the ESA Sentinels: Insights from Moosfluh Instability, Swiss Alps
Next Article in Special Issue
Estimating Peatland Water Table Depth and Net Ecosystem Exchange: A Comparison between Satellite and Airborne Imagery
Previous Article in Journal
Optimizing Window Length for Turbulent Heat Flux Calculations from Airborne Eddy Covariance Measurements under Near Neutral to Unstable Atmospheric Stability Conditions
Previous Article in Special Issue
Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 5
10.3390/rs10050671
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tropical Peatland Vegetation Structure and Biomass: Optimal Exploitation of Airborne Laser Scanning

by
Chloe Brown
1,*,
Doreen S. Boyd
1,
Sofie Sjögersten
2,
Daniel Clewley
3,
Stephanie L. Evers
4,5,6 and
Paul Aplin
7
1
School of Geography, University of Nottingham, Nottingham NG7 2RD, UK
2
School of Biosciences, University of Nottingham, Nottingham NG7 2RD, UK
3
Plymouth Marine Laboratory, Plymouth PL1 3DH, UK
4
School of Natural Sciences and Psychology, Liverpool John Moores University, Liverpool L3 3AF, UK
5
School of Environmental and Geographical Sciences, University of Nottingham Malaysia Campus, Semenyih 43500, Selangor, Malaysia
6
Tropical Catchment Research Initiative (TROCARI), Semenyih 43500, Selangor, Malaysia
7
School of Geography, Edge Hill University, Ormskirk L39 4QP, UK
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(5), 671; https://doi.org/10.3390/rs10050671
Submission received: 19 March 2018 / Revised: 16 April 2018 / Accepted: 24 April 2018 / Published: 25 April 2018
(This article belongs to the Special Issue Remote Sensing of Peatlands)
Browse Figures
Versions Notes

Abstract

:
Accurate estimation of above ground biomass (AGB) is required to better understand the variability and dynamics of tropical peat swamp forest (PSF) ecosystem function and resilience to disturbance events. The objective of this work is to examine the relationship between tropical PSF AGB and small-footprint airborne Light Detection and Ranging (LiDAR) discrete return (DR) and full waveform (FW) derived metrics, with a view to establishing the optimal use of this technology in this environment. The study was undertaken in North Selangor peat swamp forest (NSPSF) reserve, Peninsular Malaysia. Plot-based multiple regression analysis was performed to established the strongest predictive models of PSF AGB using DR metrics (only), FW metrics (only), and a combination of DR and FW metrics. Overall, the results demonstrate that a Combination-model, coupling the benefits derived from both DR and FW metrics, had the best performance in modelling AGB for tropical PSF (R2 = 0.77, RMSE = 36.4, rRMSE = 10.8%); however, no statistical difference was found between the rRMSE of this model and the best models using only DR and FW metrics. We conclude that the optimal approach to using airborne LiDAR for the estimation of PSF AGB is to use LiDAR metrics that relate to the description of the mid-canopy. This should inform the use of remote sensing in this ecosystem and how innovation in LiDAR-based technology could be usefully deployed.

Graphical Abstract

1. Introduction

Tropical Peat Swamp Forests (PSF) are unique ecosystems; their health and functionality are dependent on the interactions between forest, peat and hydrology. Any unbalance in this sensitive environment from change in one can amplify across the ecosystem and impact the multitude of services they provide, creating positive feedback loops [1,2]. Tropical PSF are thus particularly vulnerable to human disturbances (as well as natural change). This is especially the case in South East Asia where there has been a long history of tropical PSF degradation [3,4]. At an estimated 88.6 Gt, tropical PSF are one of the largest pools of terrestrial carbon [5,6], however, high volumes of deforestation and land conversion rates have transformed South East Asian PSF into one of the largest emitters of carbon globally [7,8,9]. Forest clearance and conversion not only decreases carbon stores directly due to reduction in above ground biomass (AGB), but also indirectly increases carbon emissions as a result of peat exposure [10,11]. Fire susceptibility in the landscape also increases [12,13,14], further compounding carbon losses. This, coupled with the need to understand the variability and dynamics of tropical ecosystems in general with respect to their role in the global carbon cycle [5,15], means there is an urgent need to track change in PSF via estimation of AGB over space and time. Not only will this afford understanding of carbon losses, this will also help guide tropical PSF restoration and sustainable management activities [16,17].
The structurally complex nature of tropical PSF, supporting high (50–70 m) to low (15–25 m) dense canopy forest vegetation, typically with buttresses and thick root mat floors [18], presents a challenging landscape for monitoring purposes. This is further complicated by degraded (and/or recovering) PSF generating even greater variation in forest structure, in response to disturbance events and changes in peat characteristics. Traditionally, forest AGB estimates have been based on field plot inventories, where plot measurements are used to infer AGB estimates through allometric equations [19]. This manual approach provides the most accurate AGB estimates [20], however it is labour intensive, time consuming and expensive [21]. Additionally, the extent and inaccessibility of PSF, coupled with the difficult logistics of field work posed by often waterlogged, swampy conditions, has restricted forest inventory data collection.
Development in remote sensing technology over the last two decades, specifically in Light Detection and Ranging (LiDAR) [22,23], has revolutionised the retrieval and accuracy of forest structural attributes, including AGB, across landscapes scales [24]. LiDAR data has been widely adopted in forest structural applications, both at the stand and individual tree level [25], due to its ability to characterise both vertical and horizontal structures. A common theme for many studies is the development of LiDAR-derived metrics related to height distribution, density, and intensity of returns [26,27,28]. Typically, in LiDAR AGB studies, models are developed from the relationships between field plot estimated AGB, calculated from tree allometry, and LiDAR-derived metrics [29,30,31]. Establishing these relationships between metrics and forest attributes are complex, in particular for dense, multi-layered forest canopies associated with the tropics. The majority of work conducted in this area has employed discrete return (DR) derived metrics [32], with focus on the utility of DR data for carbon accounting and environmental modelling [33,34]. Asner et al. [35] examined the effectiveness of DR LiDAR derived mean canopy height to estimate AGB in four tropical regions (Panama, Peru, Madagascar, and Hawaii). The results highlighted the value of DR LiDAR in generating high-resolution carbon maps across the tropics. However, the application of DR LiDAR is restricted by the number of returns which can penetrate through dense canopies down to the forest floor, and by the limited point measurements from the canopy and the understory vertical structure [36,37].
Full Waveform (FW) LiDAR data has the potential to provide a more detailed and comprehensive 3D view of forest canopy structure in comparison to DR sensors [38,39]. Consequently, a growing body of research has focused on developing FW metrics for forest assessment. Drake et al. [40,41] are early examples of the development of FW metrics, using large-footprint FW data (laser vegetation imaging sensor) to generate a list of metrics for AGB estimations. Height of medium energy (HOME) was demonstrated to correlate strongly with mean stem diameter, basal area and AGB. For small-footprint FW LiDAR, Wu et al. [38] explored the potential of a list of structural and statistics-based AGB predictor metrics. The results produced a high correlation between FW-derived metrics with individual tree height, foliar and biomass for a savanna environment. Pirotti et al. [42] also explored the potential for estimating AGB from small-footprint FW data, finding the median height of echo count (HOMTC) performed best at estimating AGB at plot level for a complex tropical forest.
Recently, several studies have evaluated the fusion of DR and FW metrics in forest AGB estimation [43,44,45,46]. Cao et al. [47,48] assessed the potential of DR and FW metrics, individually and in combination, as predictors of total living biomass and its components (AGB, root, foliage, branch and trunk) for sub-tropical forests. The study found metrics related to canopy height to be the strongest predictors for AGB; additionally, the combination of DR and FW metrics, by multivariate linear regression, improved AGB estimation.
The benefits of LiDAR data for monitoring tropical environments has been well established, however with the structural complexity and unique interactions between forest and peat swamp, general tropical forest models may not be transferable. Limited research has been published on the application of LiDAR in tropical PSF [49,50]. Jubanski et al. [51] and Kronseder et al. [52] examined the use of LiDAR point cloud data in AGB estimation for varied levels of degraded lowland dipterocarp PSF in Central Kalimantan, Indonesia. Both studies concluded that AGB could be estimated successfully, though with varying levels of accuracy.
According to our knowledge, no previous study has examined the use of both DR and FW metrics or the fusion of DR and FW metrics in AGB estimation for tropical PSF. This paper will examine the relationship between the AGB of a tropical PSF in North Selangor, Peninsular Malaysia, and small-footprint airborne LiDAR (DR and FW) derived metrics. This forest is of particular importance since it is one of the few large areas of PSF remaining in peninsular Malaysia [53]. Three LiDAR-based approaches are investigated for modelling AGB: (1) DR-derived metrics (only); (2) FW-derived metrics (only); (3) and a combination of DR- and FW-derived metrics. The accuracy of the models is evaluated by comparing LiDAR-based AGB estimates with field (in situ plots) measured AGB, with a view to establishing the optimal model for estimating AGB of the North Selangor PSF.

2. Materials and Methods

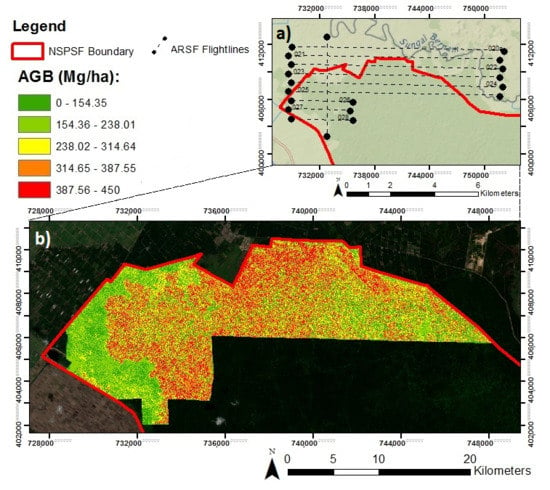
2.1. Study Site

The North Selangor Peat Swamp Forest (NSPSF) is located on the flat coastal plains of northwest Selangor, Peninsular Malaysia (Figure 1). With a combined total of 81,304 hectares, NSPSF is one of the largest remaining PSF in the region; however, over 30 years of intensive timber harvesting has left the once pristine NSPSF degraded and vulnerable to further environmental threat [18,54]. Repeated cycles of logging activities have created a complex, multi-layered canopy structure, indicated by mixed stand density and height (Figure 1). Additionally, the extraction of timber from the forest has led to the formation of a 500 km network of canals [55], scarring the forest and accelerating the drainage and erosion of valuable peat soil stores (and the carbon they hold) [53].
In response to the damaging impact of past logging activities on tropical PSF ecosystem health and the services they provide, the Selangor State Government agreed on a 25-year moratorium on timber harvesting for the State of Selangor, with all logging activities ceased in 2007 [55]. Despite this halt in logging activities, the reserve remains exposed to disturbance from the surrounding land uses, in particular accelerated drainage from Tanjong Karang Irrigation Scheme and land conversion to oil palm agriculture [57].

2.2. Field Data

To obtain field estimates of AGB, thirty circular field plots with a radius of 15 m were established within the reserve during 2017. This relatively small sample size, albeit statistically relevant, was determined by the challenging logistics of tropical PSF fieldwork, as previously mentioned. The forests plots were established to be representative of a secondary PSF ecosystem, where no obvious structural disturbances were observed since the LiDAR survey (2014)—for example major tree fall, logging activities or fire events—based on an existing forestry management plan [55], multispectral imagery and expert knowledge and experience from NSPSF Rangers. The location of the central tree, and thus the centre point of the plot, was recorded by a field GPS (Garmin GPSMAP 64), with an average horizontal error of <5 m when measurements were averaged over ten minutes. The positions of all further trees within the plot were noted relative to the centre (distance and angle) (Figure 2). For each plot, all live trees with a diameter at breast height (DBH) of >5 cm were measured and tree species recorded. Additionally, dependent on the top of tree visibility, selected trees of varying height classes were measured by a laser height meter.
An allometric equation developed by Chave et al. [19] was used to calculate AGB from field measured DBH, species (to estimate wood density), and additionally tree height when available (missing height was inferred from pantropical model). The AGB allometric equation used was:
AGB = 0.0673 × (ρD2H)0.976
where ρ = wood density (g/cm3), D = DBH (cm) and H = height (m).
The ‘BIOMASS’ package in R software (version 2.10.0) [58] was used to run AGB estimation. AGB values were calculated for individual trees within each 15 m radius field plot, and then summed to obtain a total AGB value for each plot.

2.3. LiDAR Data Acquisition

Airborne LiDAR data was flown by the UK’s Natural Environment Research Council (NERC) Airborne Research Facility (ARF) as part of its 2014 Malaysia Campaign. It is important to note the three-year time delay between the airborne LiDAR data collection (2014) and field plot inventory collection (2017). This may introduce error into the AGB models, however as previously mentioned, all field plots were established to be free from logging and fire, with no obvious disturbance within the three-year period. The data was captured in November 2014 from a Leica ALS50-II LiDAR system, a small footprint LiDAR sensor with the capacity to record both DR and FW LiDAR simultaneously. The Leica ALS50-II LiDAR system was on board a Dornier 228-201, flying at 132–136 knots at an altitude of 2145–2181 m. The sensor emits the laser beam at 1064 nm, additionally providing an intensity digital image from the return signal intensity data. The accuracy report that accompanied the LiDAR data estimated the vertical accuracy to be 0.023 m RMSE, where LiDAR elevation was assessed against ground control points. In total 29 flightlines were flown, surveying an area covering 690 km2 of the reserve and surrounding area. However, given the constraints of fieldwork and to ensure representation, a subset of the LiDAR flightlines (161.73 km2), focused on the north-west of the NSPSF reserve (Figure 3), was extracted for optimal LiDAR-derived AGB model development and assessment. The dataset has an average point density of 2.03 m2 and a point spacing of 0.70 m. The LiDAR data, DR and FW, was pre-processed by NERC’s Data Analysis Node and delivered in LAS 1.3 format.

2.4. DR-Derived Metrics

A number of descriptive structural plot-level metrics were calculated from a DR height normalised point cloud. All data processing was carried out in LAStools software [59]—a complimentary full academic LAStools licence was generously supplied through the LASmoons programme. Outliers, or noisy data, were first eliminated from the DR LAS. files supplied, and the data was then filtered to identify laser ground and non-ground (unclassified) hits. The normalised above ground heights were calculated by subtracting the ground points, interpolated into a surface using the adaptive triangulated irregular network (TIN) filtering algorithm, from the non-ground (unclassified) points. Above ground height DR metrics were then calculated. DR plot metrics included: minimum height (min), maximum height (max), average height (avg), standard deviation (std), skewness (skw), kurtosis (kur), average square height (qav), height percentile (p01, p05, p10, p25, p50, p75, p90, P9, P99), height bincentiles (b10, b20, b30, b40, b50, b60, b70, b80, b90).

2.5. FW-Derived Metrics

Informed from the success in previous studies-based in the sub-tropics [47,48], three plot-level FW metrics were derived from the recorded waveform. All data processing was carried out in the Sorted Pulse Software Library (SPDlib) [60], benefiting from the recent additions made to the metric library. Gaussian decomposition [61] was applied to each waveform to derive point information (x, y, z). Points were classified into ground or non-ground using a combination of progressive morphology filtering [62] and maximum curvature classification (MCC) [63] algorithms to produce a Digital Terrain Model (DTM), to which heights were normalised. The FW plot metrics included: height of median energy (HOME), waveform distance (WD) and roughness of the outermost canopy (ROUGH) (Figure 4). FW metrics were summarized as the mean and standard deviation for each plot.

2.6. Statistical Modelling and Analyses

Simple linear regression analysis on field measured plot AGB values against LiDAR derived DR and FW metrics was conducted. Multiple linear regression models were developed independently from the DR metrics, FW metrics and DR and FW metrics in combination for estimating AGB. To ensure model variables were not highly correlated, a ‘data mining’ approach, outlined by Langton et al. [64], was first adopted to identify the key predictor variables for multiple regression analyses. This stage was required to avoid model over-fitting given the relatively small sample size (n = 30) and potential high collinearity of a number of LiDAR metrics with one another. The ‘MuMIn’ package for R software (version 1.9.5) [65] was used to run a modified Akaike Information Criterion (AIC), termed AICc [66], this comparing the quality of predictive multiple regression model inputs. An automated stepwise AICc was performed to select input variables for the final models. The delta-AIC value was assessed for each candidate model, a threshold value for delta-AIC was set to <2, models which met this requirement were determined to be within range of plausible models that best fit the observed values [66]. The top ranked AICc regression models were assessed based on a number of diagnostics tests (ANOVA, students t-test and variance inflation factor (≤1)) to produce final predictive models for DR metrics (only), FW metrics (only), and a combination of DR and FW metrics. The final predictive modes—DR-model, FW-model, and Combination-model—were fitted and assessed based on a combination of: R-square (R2), adjusted R-square (Adj-R2), Root Mean Square Error (RMSE), and the relative Root Mean Square Error (rRMSE).
To judge the reliability of the models, leave-one-out-cross validation (LOOCV) was performed. The LOOCV method for model evaluation was selected due to its proven effectiveness for models with a small sample size [67]. The Root Mean Square Error from the cross-validation analysis (RMSEcv) and bias (BIAScv) was calculated and presented as indicators of the three models’ predictive power. Finally, to investigate the significance of the addition of FW metrics in PSF AGB estimation, the Kruskal-Wallis H test (or one-way ANOVA on ranks) was used to determine if there were statistically significant differences between the three final models’ AGB plot predictions.

3. Results

Plot-based AGB values were calculated from field measured DBH, species and height data (when available). For the 30 plots, AGB ranged from 126.96 Mg/ha to 443.27 Mg/ha, with a mean value of 319.52 Mg/ha, with a standard deviation of 76.34 Mg/ha (Table 1).
The results from simple linear regression analysis between field-based AGB estimates and 31 LiDAR derived DR and FW metrics are presented in Table 2 and Table 3. For DR metrics, the 50th height percentile (‘p50’) showed the highest correlation with field-based AGB (R2 = 0.68, RMSE = 42.1), followed by average height (‘avg’) (R2 = 0.64, RMSE = 45.2). Both minimum height (‘min’) and standard deviation (‘std’) displayed no significant relationship or sensitivity to field-based AGB. For FW metrics, the mean HOME (‘H_mean’) provided the highest correlation with field-based AGB (R2 = 0.72, RMSE = 39.4) (Figure 5). The mean input variables calculated for all FW metrics displayed a moderate correlation and significant relationship with field-based AGB, however, the standard deviation input variables calculated for all FW metrics showed very low correlation, with standard deviation HOME (‘H_sd’) and standard deviation ROUGH (‘R_sd’) presenting no significant relationship to field-based AGB estimates. It is evident from the linear regression results that metrics representing mid-canopy levels, for example ‘p50’ and ‘H_mean’, are important predictors for AGB estimation in PSF. The variation in mid-canopy structure captured by these metrics can be seen in Figure 6. Where a waveform has been extracted from the centre point (1 m buffer) for each of the 30 field plots
The results of the best models for predicting PSF AGB (DR, FW and Combination) (Table 4 are summarised in Table 5 and visualized in Figure 7. The Combination-model, H_mean/B50, displayed the best agreement with field-based AGB values (R2 = 0.77; RMSE = 36.4; rRMSE = 10.8%). Figure 8 displays an example of AGB (Mg/ha) estimates calculated from the Combination-model for a subset of the LiDAR flightlines in the northwest of the NSPSF reserve at a 5 m (0.0025 ha) spatial resolution.
However, all three predictive models displayed a strong positive correlation and a significant relationship to field-based AGB estimates (DR-model—R2 = 0.73; RMSE = 39.2; rRMSE = 12.3%) and (FW-model—R2 =0.76; RMSE = 36.9; rRMSE = 11.6%). Figure 9 displays the frequency distribution for model generated AGB (Mg/ha) values for the 30 plots, presented with model AGB (Mg/ha) summary statistics. The Kruskal-Wallis test showed that there was no statistically significant difference between the three models for PSF AGB prediction (H(2) = 0.0038095; p = 0.99). In summary, the synergistic use of DR- and FW-derived metrics displayed a stronger correlation with field-based AGB estimates in comparison to individual and multiple DR- and FW-models, however, there was no significant difference in tropical PSF AGB prediction between the three best multiple regression models (DR, FW and Combination).

4. Discussion

Quantification of tropical PSF AGB cover is required to better understand and safeguard tropical peatlands’ ecosystem function and resilience to disturbance, both natural and anthropogenic [68]. AGB products provide accurate baseline estimates to support international climate change policies and programs such as the UN REDD+ (United Nations Reducing Emissions from Deforestation and Forest Degradation), as well as the development of sustainable management strategies for local stakeholders. Additionally, knowledge gained from the precise assessment of PSF AGB distribution will assist in Malaysia’s work towards meeting their Sustainable Development Goals (SDGs), specifically relating to SDG-13 ‘Climate action’. Using a remote sensing approach to acquiring AGB estimates is attractive in that large spatial extents are covered and monitoring can be frequent, particularly once a calibrated model has been established between forest inventory and remotely sensed data. In this case, the LiDAR campaign covered 53% of the NSPSF reserve. This is the first time such data had been captured for NSPSF and used in this way. The study demonstrates the utility of both DR and FW LiDAR data for tropical PSF AGB estimation and thus illustrates the real potential for a monitoring approach underpinned by laser scanning technologies.
The AGB range presented in the in-situ plots was 126.96–443.27 Mg/ha. AGB plot values are consistent with PSF estimates from the literature [52] and therefore considered reliable and reflective of a secondary tropical PSF, with a diverse structure and density (Figure 1). The investigation is limited by the relatively small sample size (n = 30) used for model development and validation [69]. However, the training plots were identified as being representative of the PSF conditions found in NSPSF; all field plots had good correspondence with LiDAR data providing detailed information on both forest canopy and ground (mean ground-classified hits = 8.3% per plot) relative to a densely closed and partially open canopy structure (Figure 6). The study recognises that a larger sample size is advisable in future work for model validation. Nevertheless, the plots sampled in this study cover a wide range of forest types found across NSPSF, with plots positioned in high, medium, and low forest height stands with varying densities (Figure 1).
From the numerous DR and FW LiDAR metrics tested against this range in AGB measured in the in situ plots, three AGB prediction models were determined to have a high accuracy with an rRMSE <15%: one model using discrete return data only (DR-model = 12.3%), one model using full waveform data only (FW-model = 11.6%) and one model using a combination of DR and FW data (Combination-model = 10.8%). Overall, the Combination-model was best for explaining AGB, with an R2 of 0.77 (RMSE = 36.4, rRMSE = 10.8%). There was no statistically significant difference between these three best models for PSF AGB prediction.
Simple linear regression revealed LiDAR-derived metrics relating to mid-story canopy levels—for example average height, 50th height percentile, 50th height bincentile and HOME—to be the strongest predictors of AGB in tropical PSF. In this study, models which included FW metrics were dominated by the strong predictive capabilities of the mean HOME metric. Waveform derived HOME is the distance from the waveform centroid to the ‘ground’ (i.e., the ground position of the pseudo-waveform), HOME has previously been found to be sensitive to canopy openness (including tree density) and the vertical arrangement of a forest stand [40,41]. This suggests that for complex tropical PSF the often unobserved structural and compositional diversity in the lower portions of the forest canopy is crucial for accurate AGB model prediction. This observation is crucial for understanding how LiDAR technologies should be employed for optimal AGB estimation in these environments.
Focusing on the FW LiDAR data it can be seen that the mean values of all FW metrics displayed moderate to high correlations and significant relationships with in situ plot AGB values. These findings are consistent with past research in the use of FW LiDAR in forestry applications [70,71]. Reitberger et al. [72] found FW metrics to improve the detection of under and mid-story trees compared to first/last DR LiDAR by 10–15%, though the study was unable to detect 65% of mid-story trees, and 74% of understory trees in leaf on conditions. Indeed, FW LiDAR is still limited by the lack of significant transmission through dense forest leaves and stems, however its potential to improve our knowledge and understanding of multi-layered forest structures has been widely recognised by the remote sensing community [73]. Although in this study we found no statically significant enhancement (at 95% level of confidence) with the addition of FW metrics in the predictive models for AGB estimation, the full waveforms per plot do show discernible differences. Our focus here was on the use of FW LiDAR metrics common in related literature [41,42,47]. There may exist alternative FW metrics not tested here which could be implemented in future research. This could improve the already strong predictive AGB models, and also describe other structural variables in the forest. These include crown bulk density, canopy fuel weight and for larger dominant trees, crown width [74,75]. Thus, the continued development and application of FW LiDAR in future tropical PSF AGB research is recommended, with a focus on capturing and describing FW. Recent initiatives, such as the Global Ecosystems Dynamics Investigation (GEDI) LiDAR due to be deployed on the International Space Station, respond to the recognised need for vertical structure measurements of the Earth’s surface, as put forward by the host country’s (USA) National Academy of Sciences and NASA’s Science Mission Directorate [76]. The GEDI is just one example of the progress and development in LiDAR systems and platforms that should encourage the continued application of LiDAR data in future PSF applications. Other examples include advancements in small-scale sensor technology which has permitted the use of Unmanned Aerial Vehicles (UAVs) as a LiDAR sensor platform [77,78] thus profiting from potentially higher resolution data capture at a considerably lower surveying cost at local scales. Integration with hyperspectral systems could also be advantageous [79].
Of those alternative metrics which should be implemented in future tropical PSF AGB research, those relating to LiDAR intensity [80,81,82] are worth considering. Small-footprint LiDAR intensity data (amount of energy reflected back to the sensor) has been increasingly adopted in forestry applications [80,83]. Top of canopy intensity metrics, in combination with LiDAR derived height values, have been proven to contribute significantly to improved forest AGB estimations [84] and have been linked with tree species number at mid-story canopy level [85]. For this particular investigation, LiDAR intensity metrics were not included in AGB forest estimation because of uneven atmospheric conditions during the flight, therefore the resulting intensity data could not be reliably corrected for or compared between flightlines. This represents a challenge to be tackled in the future.
The results in this study demonstrate the advantage of using both DR and FW LiDAR data in tropical PSF AGB inventory programmes, which in turn provide a more detailed and accurate account of PSF structural cover and above ground carbon allocation across landscape scales. Apart from discerning the role for LiDAR in estimating AGB of these PSFs, this study has also provided in situ plot AGB data for the NSPSF, providing new PSF AGB plot data for an ecosystem underrepresented by global forest inventory databases [86,87]. This is important for subsequent research on how these forests function. As stated earlier the airborne LiDAR data does not fully cover the whole of the NSPSF reserve, in such cases satellite data (i.e., Sentinel-2 or very high-resolution systems) may be used to scale up AGB estimates across larger landscape scales [88,89]. Indeed, given how well the LiDAR estimates AGB in this environment, forward monitoring could be based on the passive satellite systems with LiDAR technologies used in a sampling capacity to provide calibration and validation data [24].

5. Conclusions

This study examined the relationship between tropical PSF AGB and small-footprint airborne LiDAR DR- and FW-derived metrics with a view to establishing the optimal use of this technology in this environment. Plot-based multiple regression analysis was performed to establish the best predictive models of PSF AGB using DR metrics (only), FW metrics (only), and a combination of DR and FW metrics. All three final models presented a high correlation with AGB estimates, with an R2 ≥ 0.73 and no statistical difference between the rRMSE of these models.
Overall, the results demonstrate that a Combination-model, coupling the benefits derived from both DR and FW metrics, had the best performance in modelling AGB for tropical PSF (R2 = 0.77, RMSE = 36.4, rRMSE = 10.8%). The study found that perhaps of greater importance is metric selection, as opposed to LiDAR data type (DR, FW, Combination) for assessing AGB prediction. In particular, the top ranked metrics in the best performing models related to mid-canopy order height metrics, this indicating the importance of suppressed tree crowns and forest structural diversity in the mid-level portions of PSF for reliable AGB assessment.
Overall, the utility of LiDAR for tropical PSF AGB mapping and monitoring is enormous. The ever-increasing role of LiDAR in supporting forestry applications is encouraged by the recent development and expansion in sensor technology and platforms, with LiDAR data more accessible and at a lower cost than ever before. Published studies on tropical PSF AGB are few, in particular for Peninsular Malaysia, thus as a result this study contributes significantly to tropical PSF ecology. The study underpins AGB estimation across the NSPSF reserve going forward and has direct applications for sustainable tropical PSF management, supporting decision and policy makers in the preservation and protection of South East Asia’s vulnerable tropical peatlands.

Author Contributions

C.B. is a PhD student and under the supervision of D.S.B. and S.S. conceived and executed the research. C.B. was assisted in the field by S.L.E. and with data processing by D.C. C.B. undertook analyses and C.B. and D.S.B. wrote the manuscripts with input from S.S. and P.A.

Acknowledgments

We would like to thank the Airborne Research Facility of the UK’s Natural Environment Research Council for providing the airborne LiDAR datasets (to PA and DB). This work was supported by the Natural Environment Research Council [NE/L002604/1], under the Envision DTP (to PA, SS, and DB). Additional support from the University of Nottingham. We are very grateful to Martin Isenburg for generously granting the project with a complimentary full academic LAStools licence, under the LASmoons programme. We would like to thank Lahirus S. Wijedasa for his assistance and guidance with fieldwork at the pilot stage of the project. Special thanks go to the Selangor State Forestry Department for granting reserve access and providing field ranger support for data collection, and sharing their expert knowledge and experiences working in the reserve.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Page, S.E.; Rieley, J.O.; Shotyk, Ø.W.; Weiss, D. Interdependence of peat and vegetation in a tropical peat swamp forest. In Changes and Disturbance in Tropical Rainforest in South-East Asia; Royal Society: London, UK, 1999; pp. 161–173. [Google Scholar]
  2. Wijedasa, L.S.; Jauhiainen, J.; Könönen, M.; Lampela, M.; Vasander, H.; Leblanc, M.C.; Evers, S.; Smith, T.E.; Yule, C.M.; Varkkey, H.; et al. Denial of long-term issues with agriculture on tropical peatlands will have devastating consequences. Glob. Chang. Biol. 2017, 23, 977–982. [Google Scholar] [CrossRef] [PubMed]
  3. Miettinen, J.; Shi, C.; Liew, S.C. Land cover distribution in the peatlands of Peninsular Malaysia, Sumatra and Borneo in 2015 with changes since 1990. Glob. Ecol. Conserv. 2016, 6, 67–78. [Google Scholar] [CrossRef]
  4. Miettinen, J.; Shi, C.; Liew, S.C. Two decades of destruction in Southeast Asia’s peat swamp forests. Front. Ecol. Environ. 2012, 10, 124–128. [Google Scholar] [CrossRef]
  5. Page, S.E.; Rieley, J.O.; Banks, C.J. Global and regional importance of the tropical peatland carbon pool. Glob. Chang. Biol. 2011, 17, 798–818. [Google Scholar] [CrossRef]
  6. Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  7. Ballhorn, U.; Siegert, F.; Mason, M.; Limin, S. Derivation of burn scar depths and estimation of carbon emissions with LIDAR in Indonesian peatlands. Proc. Natl. Acad. Sci. USA 2009, 106, 21213–21218. [Google Scholar] [CrossRef] [PubMed]
  8. Hooijer, A.; Page, S.; Canadell, J.G.; Silvius, M.; Kwadijk, J.; Wösten, H.; Jauhiainen, J. Current and future CO2 emissions from drained peatlands in Southeast Asia. Biogeosciences 2010, 7, 1505–1514. [Google Scholar] [CrossRef]
  9. Page, S.E.; Siegert, F.; Rieley, J.O.; Boehm, H.D.; Jaya, A.; Limin, S. The amount of carbon released from peat and forest fires in Indonesia during 1997. Nature 2002, 420, 61–65. [Google Scholar] [CrossRef] [PubMed]
  10. Page, S.E.; Banks, C.J.; Rieley, J.O. Tropical peatlands: Distribution, extent and carbon storage-uncertainties and knowledge gaps. Peatl. Int. 2007, 2, 26–27. [Google Scholar]
  11. Jauhiainen, J.; Takahashi, H.; Heikkinen, J.E.; Martikainen, P.J.; Vasander, H. Carbon fluxes from a tropical peat swamp forest floor. Glob. Chang. Biol. 2005, 11, 1788–1797. [Google Scholar] [CrossRef]
  12. Langner, A.; Miettinen, J.; Siegert, F. Land cover change 2002–2005 in Borneo and the role of fire derived from MODIS imagery. Glob. Chang. Biol. 2007, 13, 2329–2340. [Google Scholar] [CrossRef]
  13. Gaveau, D.L.; Salim, M.A.; Hergoualc’h, K.; Locatelli, B.; Sloan, S.; Wooster, M.; Marlier, M.E.; Molidena, E.; Yaen, H.; DeFries, R.; et al. Major atmospheric emissions from peat fires in Southeast Asia during non-drought years: Evidence from the 2013 Sumatran fires. Sci. Rep. 2014, 4, 6112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Van der Werf, G.R.; Dempewolf, J.; Trigg, S.N.; Randerson, J.T.; Kasibhatla, P.S.; Giglio, L.; Murdiyarso, D.; Peters, W.; Morton, D.C.; Collatz, G.J.; et al. Climate regulation of fire emissions and deforestation in equatorial Asia. Proc. Natl. Acad. Sci. USA 2008, 105, 20350–20355. [Google Scholar] [CrossRef] [PubMed]
  15. Murdiyarso, D.; Hergoualc’h, K.; Verchot, L.V. Opportunities for reducing greenhouse gas emissions in tropical peatlands. Proc. Natl. Acad. Sci. USA 2010, 107, 19655–19660. [Google Scholar] [CrossRef] [PubMed]
  16. Asner, G.P.; Brodrick, P.G.; Philipson, C.; Vaughn, N.R.; Martin, R.E.; Knapp, D.E.; Heckler, J.; Evans, L.J.; Jucker, T.; Goossens, B.; et al. Mapped aboveground carbon stocks to advance forest conservation and recovery in Malaysian Borneo. Biol. Conserv. 2018, 217, 289–310. [Google Scholar] [CrossRef]
  17. Sullivan, M.J.; Talbot, J.; Lewis, S.L.; Phillips, O.L.; Qie, L.; Begne, S.K.; Chave, J.; Cuni-Sanchez, A.; Hubau, W.; Lopez-Gonzalez, G.; et al. Diversity and carbon storage across the tropical forest biome. Sci. Rep. 2017, 7, 39102. [Google Scholar] [CrossRef] [PubMed]
  18. Yule, C.M.; Gomez, L.N. Leaf litter decomposition in a tropical peat swamp forest in Peninsular Malaysia. Wetl. Ecol. Manag. 2009, 17, 231–241. [Google Scholar] [CrossRef]
  19. Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
  20. Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
  21. Aplin, P. Remote sensing: Ecology. Prog. Phys. Geogr. 2005, 29, 104–113. [Google Scholar] [CrossRef]
  22. Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. For. 2000, 98, 44–46. [Google Scholar]
  23. Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
  24. Wulder, M.A.; White, J.C.; Bater, C.W.; Coops, N.C.; Hopkinson, C.; Chen, G. Lidar plots—A new large-area data collection option: Context, concepts, and case study. Can. J. Remote Sens. 2012, 38, 600–618. [Google Scholar] [CrossRef]
  25. Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.H.; et al. Area-based vs. tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
  26. Ni-Meister, W.; Lee, S.; Strahler, A.H.; Woodcock, C.E.; Schaaf, C.; Yao, T.; Ranson, K.J.; Sun, G.; Blair, J.B. Assessing general relationships between aboveground biomass and vegetation structure parameters for improved carbon estimate from lidar remote sensing. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
  27. Thapa, R.B.; Watanabe, M.; Motohka, T.; Shiraishi, T.; Shimada, M. Calibration of aboveground forest carbon stock models for major tropical forests in central Sumatra using airborne LiDAR and field measurement data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 661–673. [Google Scholar] [CrossRef]
  28. Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using lidar remote sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
  29. He, Q.; Chen, E.; An, R.; Li, Y. Above-ground biomass and biomass components estimation using LiDAR data in a coniferous forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
  30. Ni-Meister, W.; Lee, S. Allometric Relationship between Full Waveform LiDAR measurements and Above-ground Biomass. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 21–26 February 2016. [Google Scholar]
  31. Sullivan, F.B.; Ducey, M.J.; Orwig, D.A.; Cook, B.; Palace, M.W. Comparison of lidar-and allometry-derived canopy height models in an eastern deciduous forest. For. Ecol. Manag. 2017, 406, 83–94. [Google Scholar] [CrossRef]
  32. Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
  33. Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
  34. Asner, G.P.; Powell, G.V.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-resolution forest carbon stocks and emissions in the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 16738–16742. [Google Scholar] [CrossRef] [PubMed]
  35. Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; Van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
  36. Wang, C.; Menenti, M.; Stoll, M.P.; Feola, A.; Belluco, E.; Marani, M. Separation of ground and low vegetation signatures in LiDAR measurements of salt-marsh environments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2014–2023. [Google Scholar] [CrossRef]
  37. Hopkinson, C.; Chasmer, L.E.; Sass, G.; Creed, I.F.; Sitar, M.; Kalbfleisch, W.; Treitz, P. Vegetation class dependent errors in lidar ground elevation and canopy height estimates in a boreal wetland environment. Can. J. Remote Sens. 2005, 31, 191–206. [Google Scholar] [CrossRef]
  38. Wu, J.; Van Aardt, J.A.; Asner, G.P.; Kennedy-Bowdoin, T.; Knapp, D.; Erasmus, B.F.; Mathieu, R.; Wessels, K.; Smit, I.P. Lidar Waveform-Based Woody and Foliar Biomass Estimation in Savanna Environments; Rochester Institute of Technology: Rochester, NY, USA, 2009; Available online: https://www.researchgate.net/profile/Jan_Van_Aardt/publication/216859169_LiDAR_Waveform-based_Woody_and_Foliar_Biomass_Estimation_in_Savanna_Environments/links/00b7d515c456a3afb9000000.pdfb (accessed on 4 December 2017).
  39. Hancock, S.; Armston, J.; Li, Z.; Gaulton, R.; Lewis, P.; Disney, M.; Danson, F.M.; Strahler, A.; Schaaf, C.; Anderson, K.; et al. Waveform lidar over vegetation: An evaluation of inversion methods for estimating return energy. Remote Sens. Environ. 2015, 164, 208–224. [Google Scholar] [CrossRef] [Green Version]
  40. Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy neotropical forests using lidar remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
  41. Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]
  42. Pirotti, F.; Laurin, G.V.; Vettore, A.; Masiero, A.; Valentini, R. Small footprint full-waveform metrics contribution to the prediction of biomass in tropical forests. Remote Sens. 2014, 6, 9576–9599. [Google Scholar] [CrossRef]
  43. Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Li, G. Above-ground biomass estimation using airborne discrete-return and full-waveform LiDAR data in a coniferous forest. Ecol. Indic. 2017, 78, 221–228. [Google Scholar] [CrossRef]
  44. Sumnall, M.J.; Hill, R.A.; Hinsley, S.A. Comparison of small-footprint discrete return and full waveform airborne LiDAR data for estimating multiple forest variables. Remote Sens. Environ. 2016, 173, 214–223. [Google Scholar] [CrossRef]
  45. Lindberg, E.; Olofsson, K.; Holmgren, J.; Olsson, H. Estimation of 3D vegetation structure from waveform and discrete return airborne laser scanning data. Remote Sens. Environ. 2012, 118, 151–161. [Google Scholar] [CrossRef]
  46. Neuenschwander, A.L.; Magruder, L.A.; Tyler, M. Landcover classification of small-footprint, full-waveform lidar data. J. Appl. Remote Sens. 2009, 3, 033544. [Google Scholar] [CrossRef]
  47. Cao, L.; Coops, N.C.; Hermosilla, T.; Innes, J.; Dai, J.; She, G. Using small-footprint discrete and full-waveform airborne LiDAR metrics to estimate total biomass and biomass components in subtropical forests. Remote Sens. 2014, 6, 7110–7135. [Google Scholar] [CrossRef]
  48. Cao, L.; Coops, N.C.; Innes, J.; Dai, J.; She, G. Mapping above-and below-ground biomass components in subtropical forests using small-footprint LiDAR. Forests 2014, 5, 1356–1373. [Google Scholar] [CrossRef]
  49. Wan-Mohd-Jaafar, W.S.; Woodhouse, I.H.; Silva, C.A.; Omar, H.; Hudak, A.T. Modelling individual tree aboveground biomass using discrete return lidar in lowland dipterocarp forest of Malaysia. J. Trop. For. Sci. 2017, 29, 465–484. [Google Scholar]
  50. Manuri, S.; Andersen, H.E.; McGaughey, R.J.; Brack, C. Assessing the influence of return density on estimation of lidar-based aboveground biomass in tropical peat swamp forests of Kalimantan, Indonesia. International. J. Appl. Earth Obs. Geoinf. 2017, 56, 24–35. [Google Scholar] [CrossRef]
  51. Jubanski, J.; Ballhorn, U.; Kronseder, K.; Franke, J.; Siegert, F. Detection of large above-ground biomass variability in lowland forest ecosystems by airborne LiDAR. Biogeosciences 2013, 10, 3917–3930. [Google Scholar] [CrossRef]
  52. Kronseder, K.; Ballhorn, U.; Böhm, V.; Siegert, F. Above ground biomass estimation across forest types at different degradation levels in Central Kalimantan using LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 37–48. [Google Scholar] [CrossRef]
  53. Ahmad, N. Guardians of the North Selangor Peat Swamp Forest. 2014. Available online: https://peatlandsinternational.wordpress.com/2014/06/20/peatlands-international-2-2014/ (accessed on 20 June 2014).
  54. Prentice, C.; Aikanathan, S. A Preliminary Faunal Survey of the North Selangor Peat Swamp Forest; World Wildlife Fund Malaysia: Petaling Jaya, Malaysia, 1989. [Google Scholar]
  55. Parish, F.; Dahalan, M.; Rahim, H. Integrated Management Plan for North Selangor Peat Swamp Forest 2014–2023 for Selangor State Forestry Department; Draft (30 June 2014) Revision 2.4; Global Environment Centre: Petaling Jaya, Malaysia, 2014. [Google Scholar]
  56. Regional Centre for Forest Management (RCFM) and Ecosystem Management Services (EMS). Report on The Management Inventory of the North Selangor Peat Swamp Forest; Malaysian-DANCED Project on Sustainable Managment of Peat Swamp Forest; Project Document Number 25; Malaysia Office: Petaling Jaya, Malaysia, 2000.
  57. Tonks, A.J.; Aplin, P.; Beriro, D.J.; Cooper, H.; Evers, S.; Vane, C.H.; Sjögersten, S. Impacts of conversion of tropical peat swamp forest to oil palm plantation on peat organic chemistry, physical properties and carbon stocks. Geoderma 2017, 289, 36–45. [Google Scholar] [CrossRef]
  58. Rejou-Mechain, M.; Tanguy, A.; Piponiot, C.; Chave, J.; Herault, B. BIOMASS: Estimating Aboveground Biomass and Its Uncertainty in Tropical Forests. 2017. R Package Version 1.1. Available online: https://CRAN.R-project.org/package=BIOMASS (accessed on 2 October 2017).
  59. LAStools, “Efficient LiDAR Processing Software” (Version 141017, Academic). Available online: http://rapidlasso.com/LAStools (accessed on 2 October 2017).
  60. Bunting, P.; Armston, J.; Clewley, D.; Lucas, R.M. Sorted pulse data (SPD) library—Part II: A processing framework for LiDAR data from pulsed laser systems in terrestrial environments. Comput. Geosci. 2013, 56, 207–215. [Google Scholar] [CrossRef]
  61. Wagner, W.; Ullrich, A.; Melzer, T.; Briese, C.; Kraus, K. From Single-Pulse to Full-Waveform Airborne Laser Scanners: Potential and Practical Challenges. 2 July 2004. Available online: http://www.isprs.org/proceedings/XXXV/congress/comm3/papers/267.pdf (accessed on 10 October 2017).
  62. Zhang, K.; Chen, S.C.; Whitman, D.; Shyu, M.L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
  63. Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return LiDAR in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
  64. Langton, S.D.; Briggs, P.A.; Haysom, K.A. Daubenton’s bat distribution along rivers–developing and testing a predictive model. Aquat. Conserv. Mar. Freshw. Ecosyst. 2010, 20. [Google Scholar] [CrossRef]
  65. Barton, K. MuMIn: Multi-Model Inference. 2017. R Package Version 1.40.0. Available online: https://CRAN.R-project.org/package=MuMIn (accessed on 20 November 2017).
  66. Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: Berlin, Germany, 2003. [Google Scholar]
  67. Peduzzi, A.; Wynne, R.H.; Fox, T.R.; Nelson, R.F.; Thomas, V.A. Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data. For. Ecol. Manag. 2012, 270, 54–65. [Google Scholar] [CrossRef]
  68. Lawson, I.T.; Kelly, T.J.; Aplin, P.; Boom, A.; Dargie, G.; Draper, F.C.; Hassan, P.N.; Hoyos-Santillan, J.; Kaduk, J.; Large, D.; et al. Improving estimates of tropical peatland area, carbon storage, and greenhouse gas fluxes. Wetl. Ecol. Manag. 2015, 23, 327–346. [Google Scholar] [CrossRef]
  69. Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
  70. Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform LiDAR data. Int. J. Wildl. Fire 2014, 23, 224–233. [Google Scholar] [CrossRef]
  71. Richardson, J.J.; Moskal, L.M. Strengths and limitations of assessing forest density and spatial configuration with aerial LiDAR. Remote Sens. Environ. 2011, 115, 2640–2651. [Google Scholar] [CrossRef]
  72. Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
  73. Bye, I.J.; North, P.R.; Los, S.O.; Kljun, N.; Rosette, J.A.; Hopkinson, C.; Chasmer, L.; Mahoney, C. Estimating forest canopy parameters from satellite waveform LiDAR by inversion of the FLIGHT three-dimensional radiative transfer model. Remote Sens. Environ. 2017, 188, 177–189. [Google Scholar] [CrossRef]
  74. Unger, D.R.; Hung, I.K.; Brooks, R.; Williams, H. Estimating number of trees, tree height and crown width using Lidar data. GISci. Remote Sens. 2014, 51, 227–238. [Google Scholar] [CrossRef]
  75. Alexander, C.; Korstjens, A.H.; Hill, R.A. Influence of micro-topography and crown characteristics on tree height estimations in tropical forests based on LiDAR canopy height models. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 105–113. [Google Scholar] [CrossRef]
  76. Science Beta, NASA, National Academy of Sciences and NASA’s Science Mission Directorate 2016. Available online: https://science.nasa.gov/missions/gedi (accessed on 13 February 2018).
  77. Wallace, L.; Lucieer, A.; Watson, C.S. Evaluating tree detection and segmentation routines on very high resolution UAV LiDAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
  78. Shang, X.; Chazette, P. Interest of a full-waveform flown UV lidar to derive forest vertical structures and aboveground carbon. Forests 2014, 5, 1454–1480. [Google Scholar] [CrossRef]
  79. Pang, Y.; Li, Z.; Ju, H.; Lu, H.; Jia, W.; Si, L.; Guo, Y.; Liu, Q.; Li, S.; Liu, L.; et al. LiCHy: The CAF’s LiDAR, CCD and hyperspectral integrated airborne observation system. Remote Sens. 2016, 8, 398. [Google Scholar] [CrossRef]
  80. Kim, S.; McGaughey, R.J.; Andersen, H.E.; Schreuder, G. Tree species differentiation using intensity data derived from leaf-on and leaf-off airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1575–1586. [Google Scholar] [CrossRef]
  81. Moffiet, T.; Mengersen, K.; Witte, C.; King, R.; Denham, R. Airborne laser scanning: Exploratory data analysis indicates potential variables for classification of individual trees or forest stands according to species. ISPRS J. Photogramm. Remote Sens. 2005, 59, 289–309. [Google Scholar] [CrossRef]
  82. Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform LIDAR data for the classification of deciduous and coniferous trees. Int. J. Remote Sens. 2008, 29, 1407–1431. [Google Scholar] [CrossRef]
  83. Sumnall, M.; Fox, T.R.; Wynne, R.H.; Thomas, V.A. Mapping the height and spatial cover of features beneath the forest canopy at small-scales using airborne scanning discrete return Lidar. ISPRS J. Photogramm. Remote Sens. 2017, 133, 186–200. [Google Scholar] [CrossRef]
  84. Li, M.; Im, J.; Quackenbush, L.J.; Liu, T. Forest biomass and carbon stock quantification using airborne LiDAR data: A case study over Huntington wildlife forest in the Adirondack Park. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3143–3156. [Google Scholar] [CrossRef]
  85. Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
  86. Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above-and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
  87. Manuri, S.; Brack, C.; Nugroho, N.P.; Hergoualc’h, K.; Novita, N.; Dotzauer, H.; Verchot, L.; Putra, C.A.; Widyasari, E. Tree biomass equations for tropical peat swamp forest ecosystems in Indonesia. For. Ecol. Manag. 2014, 334, 241–253. [Google Scholar] [CrossRef]
  88. Mora, B.; Wulder, M.A.; Hobart, G.W.; White, J.C.; Bater, C.W.; Gougeon, F.A.; Varhola, A.; Coops, N.C. Forest inventory stand height estimates from very high spatial resolution satellite imagery calibrated with lidar plots. Int. J. Remote Sens. 2013, 34, 4406–4424. [Google Scholar] [CrossRef]
  89. Wilkes, P.; Jones, S.D.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A.K. Mapping forest canopy height across large areas by upscaling ALS estimates with freely available satellite data. Remote Sens. 2015, 7, 12563–12587. [Google Scholar] [CrossRef]
Remotesensing 10 00671 g001 550
Figure 1. (a) The location of the North Selangor Peat Swamp Forest in Peninsular Malaysia; (b) Magnified study area map at bottom left corner shows forest type (forest height (high, medium, low) and forest density (high, medium, low)) results from a forest management inventory undertaken in 2000 [56].
Figure 1. (a) The location of the North Selangor Peat Swamp Forest in Peninsular Malaysia; (b) Magnified study area map at bottom left corner shows forest type (forest height (high, medium, low) and forest density (high, medium, low)) results from a forest management inventory undertaken in 2000 [56].
Remotesensing 10 00671 g001
Remotesensing 10 00671 g002 550
Figure 2. Example field inventory plot design.
Figure 2. Example field inventory plot design.
Remotesensing 10 00671 g002
Remotesensing 10 00671 g003 550
Figure 3. (a) ARSF LiDAR flightlines; (b) LiDAR flightline subset; (c,d) field plot locations.
Figure 3. (a) ARSF LiDAR flightlines; (b) LiDAR flightline subset; (c,d) field plot locations.
Remotesensing 10 00671 g003
Remotesensing 10 00671 g004 550
Figure 4. Illustration of FW metrics location on an example pseudo-vertical waveform from the NSPSF FW dataset. Plotted Amplitude (DN)/Time (ns).
Figure 4. Illustration of FW metrics location on an example pseudo-vertical waveform from the NSPSF FW dataset. Plotted Amplitude (DN)/Time (ns).
Remotesensing 10 00671 g004
Remotesensing 10 00671 g005 550
Figure 5. Field measured AGB modelled by the mean value from the FW mean HOME metric (H_mean). Bands represent the 95% confidence envelope.
Figure 5. Field measured AGB modelled by the mean value from the FW mean HOME metric (H_mean). Bands represent the 95% confidence envelope.
Remotesensing 10 00671 g005
Remotesensing 10 00671 g006a 550Remotesensing 10 00671 g006b 550
Figure 6. Centre point (1 m buffer) plot vegetation profiles, each waveform height has been subtracted from LiDAR derived DTM; graphs are fitted Height (m)/Amplitude (DN). Height scale (y-axis) ranges from 0 to 40 m, and the amplitude (x-axis) from 0 to 120 DN. Graphs are accompanied with forest canopy structure description.
Figure 6. Centre point (1 m buffer) plot vegetation profiles, each waveform height has been subtracted from LiDAR derived DTM; graphs are fitted Height (m)/Amplitude (DN). Height scale (y-axis) ranges from 0 to 40 m, and the amplitude (x-axis) from 0 to 120 DN. Graphs are accompanied with forest canopy structure description.
Remotesensing 10 00671 g006aRemotesensing 10 00671 g006b
Remotesensing 10 00671 g007 550
Figure 7. Predicted vs field measured AGB from the best performing models: (a) DR-model; (b) FW-model; (c) Combination-model. Bands represent the 95% confidence envelope.
Figure 7. Predicted vs field measured AGB from the best performing models: (a) DR-model; (b) FW-model; (c) Combination-model. Bands represent the 95% confidence envelope.
Remotesensing 10 00671 g007
Remotesensing 10 00671 g008 550
Figure 8. (a) LiDAR flightline subset; (b) estimation of AGB (Mg/ha) within the NSPSF boundary calculated from the Combination-model, at a 5 m (0.0025 ha) spatial resolution, overlaid on Sentinel-2 multispectral image.
Figure 8. (a) LiDAR flightline subset; (b) estimation of AGB (Mg/ha) within the NSPSF boundary calculated from the Combination-model, at a 5 m (0.0025 ha) spatial resolution, overlaid on Sentinel-2 multispectral image.
Remotesensing 10 00671 g008
Remotesensing 10 00671 g009 550
Figure 9. Frequency distribution for DR-, FW- and Combination-model generated AGB (Mg/ha) across the 30 field plots, presented with model generated plot minimum, maximum, mean and standard deviation AGB (Mg/ha).
Figure 9. Frequency distribution for DR-, FW- and Combination-model generated AGB (Mg/ha) across the 30 field plots, presented with model generated plot minimum, maximum, mean and standard deviation AGB (Mg/ha).
Remotesensing 10 00671 g009
Table
Table 1. Plot measured forest parameters.
Table 1. Plot measured forest parameters.
Plot MeasurementsValues: Mean (Std Dev)
Min/Max
Tree number89.33 (21.09)
39/128
DBH (cm)46.39 (37.16)
17/375
AGB (Mg/ha)319.52 (76.34)
126.96/443.27
Table
Table 2. Results from simple linear regression using DR metrics. Values underlined represent metrics of non-significance p > 0.05.
Table 2. Results from simple linear regression using DR metrics. Values underlined represent metrics of non-significance p > 0.05.
DR MetricR2Adj-R2RMSE (Mg/ha)rRMSE (%)
Min0.040.0173.423
Max0.210.1866.620.8
Avg0.640.6245.214.2
Qav0.590.584815
Std0.10.0771.222.3
Ske0.610.646.714.6
Kur0.230.2165.720.6
P010.290.2663.419.8
P050.290.2663.419.8
P100.300.2862.719.6
P250.580.5748.515.2
P500.680.6742.113.2
P750.580.5648.915.3
P900.390.3658.818.4
P950.300.2862.719.6
P990.250.226520.3
B100.250.226520.3
B200.350.3360.619
B300.490.4853.416.7
B400.590.5748.115.1
B500.620.6146.314.5
B600.520.5151.816.2
B700.390.3758.618.4
B800.250.2364.920.3
B900.160.1368.921.5
Table
Table 3. Results from simple linear regression using FW metrics. Values underlined represent metrics of non-significance p > 0.05.
Table 3. Results from simple linear regression using FW metrics. Values underlined represent metrics of non-significance p > 0.05.
FW MetricR2Adj-R2RMSE (Mg/ha)rRMSE (%)
H_mean0.720.7139.412.3
H_sd0.00−0.037523.5
W_mean0.570.5549.315.4
W_sd0.170.1468.521.4
R_mean0.610.5947.114.7
R_sd0.00−0.0475.123.5
Table
Table 4. Model equations.
Table 4. Model equations.
Model Equations
DR=81.786 + 8.940 × P75 − 78.063 × Ske
FW=101.457 + 19.579 × H_mean − 12.555 × W_sd
Combination=171.3731 + 14.7802 × H_mean − 1.5752 × B50
Table
Table 5. Results from the best preforming models for predicting AGB.
Table 5. Results from the best preforming models for predicting AGB.
Model VariablesR2Adj-R2RMSE (Mg/ha)RMSEcv (Mg/ha)BIAScv (Mg/ha)rRMSE (%)
DRP75 Ske0.730.7139.242.9−0.8312.3
FWH_mean W_sd0.760.7436.940.9−0.1711.6
CombinationH_mean B500.770.7536.439.80.3810.8

Share and Cite

MDPI and ACS Style

Brown, C.; Boyd, D.S.; Sjögersten, S.; Clewley, D.; Evers, S.L.; Aplin, P. Tropical Peatland Vegetation Structure and Biomass: Optimal Exploitation of Airborne Laser Scanning. Remote Sens. 2018, 10, 671. https://doi.org/10.3390/rs10050671

AMA Style

Brown C, Boyd DS, Sjögersten S, Clewley D, Evers SL, Aplin P. Tropical Peatland Vegetation Structure and Biomass: Optimal Exploitation of Airborne Laser Scanning. Remote Sensing. 2018; 10(5):671. https://doi.org/10.3390/rs10050671

Chicago/Turabian Style

Brown, Chloe, Doreen S. Boyd, Sofie Sjögersten, Daniel Clewley, Stephanie L. Evers, and Paul Aplin. 2018. "Tropical Peatland Vegetation Structure and Biomass: Optimal Exploitation of Airborne Laser Scanning" Remote Sensing 10, no. 5: 671. https://doi.org/10.3390/rs10050671

APA Style

Brown, C., Boyd, D. S., Sjögersten, S., Clewley, D., Evers, S. L., & Aplin, P. (2018). Tropical Peatland Vegetation Structure and Biomass: Optimal Exploitation of Airborne Laser Scanning. Remote Sensing, 10(5), 671. https://doi.org/10.3390/rs10050671

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop