Remote Sensing of Sub-Surface Suspended Sediment Concentration by Using the Range Bias of Green Surface Point of Airborne LiDAR Bathymetry

Abstract

Suspended sediment concentrations (SSCs) have been retrieved accurately and effectively through waveform methods by using green-pulse waveforms of airborne LiDAR bathymetry (ALB). However, the waveform data are commonly difficult to analyze. Thus, this paper proposes a 3D point-cloud method for remote sensing of SSCs in calm waters by using the range biases of green surface points of ALB. The near water surface penetrations (NWSPs) of green lasers are calculated on the basis of the green and reference surface points. The range biases (ΔS) are calculated by using the corresponding NWSPs and beam-scanning angles. In situ measured SSCs (C) and range biases (ΔS) are used to establish an empirical C-ΔS model at SSC sampling stations. The SSCs in calm waters are retrieved by using the established C-ΔS model. The proposed method is applied to a practical ALB measurement performed by Optech Coastal Zone Mapping and Imaging LiDAR. The standard deviations of the SSCs retrieved by the 3D point-cloud method are less than 20 mg/L.

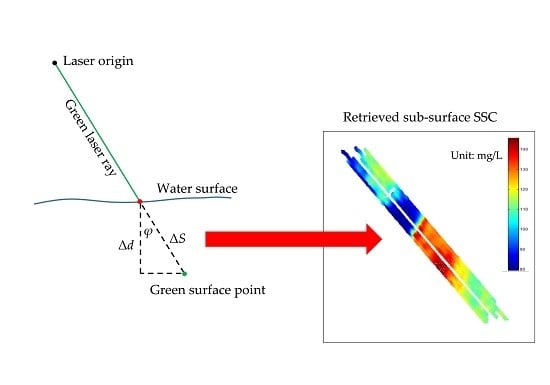
1. Introduction

Suspended sediment concentration (SSC) is an important parameter in studies of water quality, erosion, and aquatic ecological systems [1]. Information about the spatial distributions of SSC is useful because the transport of suspended sediments can affect anthropogenic activities by in-filling harbors and shipping channels and the fouling of marine instruments. In addition, the presence or absence of suspended sediment affects marine organisms by regulating light availability and acting as a transport agent for nutrients, pollutants, and biological materials [2]. The degradation of water quality due to increased SSC has also become a major global environmental problem [3]. Commonly used in situ measurement of SSC is time-consuming, labor-intensive, and provides only data at gauging station [1]. Optical remote sensing instruments (e.g., airborne LiDAR bathymetry (ALB)) can observe large areas over short timescales and provide much more spatial coverage than that of in situ sampling [2]. Specific LiDAR systems were designed to measure property profiles of the water column by transmitting linearly polarized light [4], such as airborne polarized LiDAR [5], NOAA fish LiDAR [6], and K-meter survey system [7]. ALB is an accurate, cost-effective, and rapid technique for shallow water measurements [8]. In addition to bathymetric measurement, ALB can also be used for remote sensing turbidity or SSC [9]. To date, ALB systems have been evaluated to characterize the turbidity or SSC by waveform methods, which use green-pulse waveforms [10,11,12,13,14,15]. According to the means of obtaining the waveform parameters, the waveform method comprises direct method [13,14], decomposition method [15], and deconvolution method. The direct method uses fitting functions to directly fit the water column part in a raw pulse waveform. This method is simple and effective, and it can directly extract waveform parameters to retrieve SSC in deep waters. Nevertheless, the direct method is ineffective in shallow waters, where the range of the volume backscatter return is short or missing in the raw pulse waveform [14]. Zhao et al. [15] proposed a decomposition method for the remote sensing of SSCs in shallow waters based on waveform decomposition with high accuracy. The waveform parameters are calculated on the basis of the volume backscatter return separated from the raw pulse waveform to establish empirical SSC models and retrieve SSCs. However, the waveform methods are complex and inconvenient for applications because the waveform data are commonly difficult to analyze.

The 3D point-cloud data are easily obtained and utilized compared with waveform data. Given their water-surface uncertainty [8], green lasers can hardly detect accurate water surface, but they reflect a certain level of penetration into the water column. Such penetration is referred to as the near water surface penetration (NWSP) of green lasers [16]. NWSP can be obtained by subtracting the reference surface height from green surface height [17]. The NWSP of the green laser has been researched by using theoretical analysis [18], statistical analysis [16,19], and empirical modeling [17] methods. Guenther [18] theoretically analyzed the generation mechanism of the NWSP and identified the significant factors (i.e., hydrologic conditions and ALB system parameters). Mandlburger et al. [16] used the water-surface height derived from the IR laser as a reference to statistically analyze the distributions of the NWSP in ponds and rivers. Results show that the NWSP ranges from 10 cm to 25 cm [16]. Saylam et al. [19] analyzed the water surface output by Leica LiDAR Survey Studio and found that the median difference between class 0 (derived water surface) and class 5 (green wavelength) is high in turbid conditions. They pointed out the challenges of reliable surface detection for turbid waters [19]. Zhao et al. [17] proposed an empirical NWSP model by using a stepwise regression in consideration of surface SSC, beam scanning angle, and sensor height to correct the water-surface and bottom heights of single green lasers. In calm waters, the contribution of the sub-surface SSC on the NWSP is the largest among all the significant factors [17]. These methods broaden the understanding of NWSPs and show that the potential of the NWSP in calm waters can be used as a predictor of SSC or water turbidity. The NWSP of the green laser in calm waters depends on the water transparency and ALB system parameters [18]. Conversely, an analysis on the spatial distribution of NWSPs in calm waters enables the estimation of turbidity. SSC in calm waters can be retrieved by building an empirical relationship model between SSCs and NWSPs. Therefore, in the present study, the remote sensing of sub-surface SSC by using range bias of green surface point is proposed to obtain SSCs in calm waters efficiently. This paper is structured as follows. Section 2 provides the theoretical basis of the 3D point-cloud method. Section 3 validates and analyzes the 3D point-cloud method by experiments. Section 4 provides the corresponding discussions. Section 5 presents the conclusions and recommendations obtained from the experiments and discussions.

2. Method

2.1. Traditional Waveform Method

As shown in Figure 1, a conceptual green LiDAR return waveform (amplitude vs. time) comprises the following principal components: surface return, volume backscatter return, and bottom return [8]. The surface return is a linear superposition of the energy reflected from the actual air/water interface and the energy backscattered from particulate materials in the water volume under the interface [8]. Volume backscatter denotes the signature of pulse energy reflected from particulate materials in the water column. The parameters of the volume backscatter return (i.e., slope and amplitude) are related to water clarity, and they can be used to determine water turbidity or SSC [15]. With the establishment of empirical relationship models between in situ measured SSCs and extracted waveform parameters, the SSC can be retrieved [15,20] as follows:

$$C=f(X)$$

(1)

where C is SSC, and X is the parameter of the volume backscatter. To date, the relationship between water turbidity and parameters of volume backscatter has been investigated, and results have demonstrated the capability of using ALB for detecting, mapping, and monitoring water turbidity or SSC [11,12,13,14,15]. Nonetheless, the waveform methods are complex and inconvenient for applications because the waveform data are commonly difficult to utilize. Thus, a simple and fast retrieving method has yet to be developed.

2.2. 3D Point-Cloud Method

ALB systems can be categorized into integrated IR and green ALB systems or single green ALB systems according to the wavelengths of lasers used [17]. In an integrated IR and green ALB system (e.g., Optech Coastal Zone Mapping and Imaging LiDAR (CZMIL), AHAB HawkEye III, RIEGL VQ-880-G, or Leica Chiroptera II), the IR laser (1064 nm) is selected to detect the water surface accurately, and green laser (532 nm or 515 nm (Leica Chiroptera II)) is used to detect the bottom [21]. The IR and green lasers can be emitted by a collinear (e.g., Optech CZMIL) or a non-collinear model (e.g., AHAB HawkEye III, RIEGL VQ-880-G, and Leica Chiroptera II). In a single green ALB system (e.g., Fugro LADS LADS-MK3, Optech Aquarius, USGS Experimental Advanced Airborne Research LiDAR (EAARL) and EAARL-B, or RIEGL VQ-820-G), the single green laser (532 nm) is used to detect both the surface and bottom. Due to the ability of the green signal to penetrate water, the surface returns do not exactly represent the water surface; however, depending on environmental parameters like turbidity, a certain penetration into the water column can be observed [16]. With the external water-surface height as a reference (Figure 2), the NWSP (Δd) of each green pulse can easily be calculated by subtracting the reference water surface height from the green surface height [17]. Δd can be obtained by the following equation:

$$\Delta d=H_{green}^s-H_0$$

(2)

where $H_{green}^s$ and H₀ are the heights of the green surface point and the reference surface point, respectively. In an integrated IR and green ALB system, the water-surface height derived by IR laser can be regarded as a reference. For a single green ALB system, GPS and leveling measurement can provide the reference water-surface height in calm waters [17].

The green surface return is a linear superposition of the energy reflected from the actual air/water interface and the energy backscattered from particulate materials in the water volume under the interface [8]. Waveform detection algorithms are used for the point detections of the waveforms of the IR and green lasers (Figure 3). The detected points are used to calculate the slant distance of the laser propagation and obtain the 3D surface point further. Several different algorithms, such as peak detection [22,23], leading edge detection [24,25,26], waveform decomposition [27,28,29], and deconvolution method [30,31], have been proposed to detect the features/targets of interest in pulse waveforms. The surface point derived by IR waveform can accurately represent the water surface [8]. Given the influence of volume backscatter, the round-trip time (t₂) of the green surface return in the air presents a time delay Δt with respect to the true round-trip time (t₁).

$$\Delta t=t_2-t_1$$

(3)

The individual contributions from the interface and the volume can hardly be quantified. Thus, an accurate equation between Δt and its influence factors is difficult to provide. In calm water, the time delay (Δt) evidently depends on pulse width and turbidity [18]. In waters with specular reflection (in case a wave front is oriented toward the sensor), the interface return plays an important role in green surface return and causes early arrivals of the green laser pulse echo [32]. In this case, a stable relationship model between the time delay and turbidity is difficult to establish. This study mainly focuses on calm waters, where the time delay can be connected to turbidity.

Zhao et al. [17] provided the relationship between the time delay Δt and the range bias ΔS as follows:

$$\Delta t=2\Delta S/c_{air}$$

(4)

where c_air is the velocity of the laser in the air. The range bias ΔS is proportional to Δt. If ΔS can be obtained, then the SSC in calm waters can be retrieved by establishing an empirical model between ΔS and SSC. ΔS can be calculated by the following equation:

$$\Delta S=\Delta d/\cos (\phi )$$

(5)

where $\phi$ is the beam-scanning angle. Thus, the sub-surface SSC can be estimated by establishing an empirical relationship model, which is a function of the Δd (or NWSP) and beam-scanning angle.

$$C=f(\Delta d/\cos (\phi ))$$

(6)

The model can be established by using the measured SSCs, beam-scanning angle, and NWSPs in SSC sampling stations based on a non-linear least-squares fitting method. As opposed to the waveform method, the 3D point-cloud method shows no dependence on the extraction and analysis of waveform data, which results in its easy implementation.

2.3. Steps of Point-Cloud Method

Figure 4 shows the process for remote sensing of SSCs in calm waters using the 3D point-cloud method. The process of SSC retrieving is described as follows:

Step1:

Extract the green surface points.

Step2:

Provide the reference surface points (e.g., IR laser, GPS, or leveling measurements).

Step3:

Filter the non-water surface points (e.g., boats, structures, and birds) from the raw 3D point-cloud data.

Step4:

Calculate the NWSP Δd of each pulse by using the green surface height and reference surface height.

Step5:

Calculate the range bias ΔS by using the corresponding NWSP and the beam-scanning angle.

Step6:

Establish the empirical SSC model (C-ΔS) by using the measured SSCs and the range biases at the SSC sampling stations.

Step7:

Estimate SSC at each pulse spot by inputting the corresponding NWSP and beam-scanning angle into the constructed C-ΔS model.

3. Experiment and Analysis

3.1. Data Acquisition

ALB measurements were performed by Optech CZMIL on 27 December 2014 in a shallow coastal water area near Lianyungang, Jiangsu Province, China. CZMIL is an airborne mapping system designed to provide high-resolution 3D information of the coastal environment both above the water and below [33]. CZMIL uses an active, Q-switched, Nd:YVO₄ laser that produces an infrared output at 1064 nm and a simultaneous, collinear, frequency-doubled green output of 3 mJ at 532 nm. The pulse repetition rate is 10 kHz, and the pulse width is 2 ns. A full-circular scan pattern operating at 27 Hz, which is fixed at an off-nadir angle of 20°, is utilized. The nominal spot diameter of green pulse is 2.4 m [34,35]. The 3D surface point clouds of IR and green lasers were calculated and outputted by the random post-processing software. During the ALB measurement, four suspended sediment samplings were obtained from the same water area. Seawater samples were collected using horizontal water samplers in situ and analyzed in the laboratory. Each water sample was filtered, dried, and weighed. The sub-surface SSC at station 1–4 are 122, 134, 110, and 185 mg/L, respectively. Figure 5 shows the locations and scopes of the different measurements.

3.2. Establishing the C-ΔS Model

The water area (100 m × 100 m) around each sampling station was selected as a representative sampling domain. In the four representative locations, 1018 green surface points were obtained after filtering. With the use of the water-surface height of the IR laser as a reference, the NWSP (Δd) of each green pulse can be calculated using Equation (2). The beam-scanning angle of each pulse was extracted from raw ALB files.

Table 1. Statistical parameters of the near water surface penetration (Δd) and beam-scanning angle (φ) in the four representative waters. SD: standard deviation.

Station Number	Pulse Numbers	Δd (cm)				φ (Degree)
		Max.	Min.	Mean.	SD	Max.	Min.	Mean.	SD
1	241	30.5	23.1	27.2	1.77	20.28	18.40	19.55	0.77
2	361	31.6	25.0	28.4	1.70	20.67	18.94	19.71	0.44
3	220	29.0	22.4	25.8	1.71	20.58	19.33	20.22	0.25
4	196	33.8	29.3	31.7	1.20	22.64	19.83	20.89	0.67

provides the corresponding statistical parameters of the NWSP and beam-scanning angle of each sampling station. Δd ranges from 22.4 cm to 33.8 cm at the four sampling stations, and the beam-scanning angle is approximately 20°.

To reduce the influence of systematic and random errors of 3D point-cloud data [36], each sampling domain is divided into four regions (Figure 6). The range bias (ΔS) of each green pulse is calculated by using the corresponding NWSP and beam-scanning angle. The mean range bias of each region is calculated.

Table 2. Statistical parameters of the green laser’s range biases of 16 regions (cm).

Station Number	Region	Pulse Numbers	Max.	Min.	Mean	SD
1	A	12	31.1	25.6	27.88	1.46
	B	76	31.7	24.4	28.24	1.76
	C	25	32.2	25.1	28.56	2.10
	D	128	32.7	24.8	29.45	1.87
2	A	69	33.4	26.7	29.71	1.64
	B	102	33.6	26.5	30.11	1.78
	C	70	33.5	26.7	30.49	1.85
	D	120	33.7	26.5	30.29	1.82
3	A	16	30.4	24.2	26.75	1.71
	B	54	30.8	24.2	26.96	1.62
	C	108	30.9	24.3	28.11	1.76
	D	42	30.9	23.8	27.33	1.87
4	A	59	37.8	30.2	34.35	1.83
	B	50	37.6	30.1	34.13	2.21
	C	43	37.3	30.3	33.75	1.83
	D	44	37.6	30.3	33.25	1.96

presents the corresponding statistical parameters of range bias ΔS of each region. The relationship between the measured SSC and the mean range biases of 16 regions are shown in Figure 7.

According to the relationship shown in Figure 7, the C-ΔS model can be described as follows:

$$C=a{(\Delta d/\cos (\phi ))}^b+c$$

(7)

where C is the SSC (mg/L), Δd is the NWSP (cm), $\phi$ is beam scanning angle, and a, b, and c are the model coefficients. With the use of the mean range biases of 16 regions, the model coefficients are estimated and listed in

Table 3. Regression coefficients of the C-ΔS model.

Model Coefficients	Value	95% Confidence Bounds
a	8.123 × 10−7	(−9.842 × 10−6, 1.147 × 10−5)
b	5.303	(1.691, 8.916)
c	78.06	(35.29, 120.8)

. The goodness of fit R² of the C-ΔS model is 0.966. The root mean square error (RMSE, σ) of the C-ΔS model is 5.43 mg/L. The black and dotted red lines in Figure 7 denote the regression curve and 95 percent confidence bounds (2σ) of the C-ΔS model, respectively. All the mean range biases of 16 regions are within the confidence bounds. R² and Figure 7 show that the C-ΔS model fits the measured SSCs well.

3.3. Precision Analysis

The SSCs at each pulse spot of four representative waters are estimated using the C-ΔS model. The SSC measured in situ at each station can be used as a reference to assess the internal precision of the C-ΔS model. Figure 8 displays the probability density distribution of the SSC deviations obtained by the C-ΔS model. The standard deviations of the SSC deviations of station 1–4 are 16.3, 18.3, 11.54, and 19.9 mg/L, respectively. The precision is lower than that of the waveform method [15], which achieves the standard deviation of 4.8 mg/L in the same area. Nevertheless, the proposed method provides a simple and effective way to obtain SSC.

3.4. Remote Sensing of SSCs

The SSCs at each pulse spot of the measured water area is estimated by the C-ΔS model.

(1) A total of 140,655 surface points of green laser and corresponding IR surface points are extracted from the seven-strips raw point-cloud data. Non-water-surface points are filtered using a threshold method. Figure 9a,b show the 3D point-cloud data of the green and IR lasers, respectively. With the WGS-84 ellipsoid as a reference, the heights of the water-surface points of the IR lasers range from 0.234 m to 1.723 m, and those of the green lasers vary from 0.005 m to 1.495 m.

(2) The NWSP of each green pulse is calculated by using the surface heights of the corresponding green and IR lasers. The NWSPs in the experimental water area range from 0.02 m to 0.476 m (Figure 9c). Subsequently, the range bias of each pulse is obtained by using the NWSP and corresponding beam-scanning angle. The range biases in the experimental water area range from 0.05 m to 0.51 m (Figure 9d).

(3) The SSC of each pulse spot is estimated by the established C-ΔS model through inputting the corresponding NWSP and beam-scanning angle. A moving average method is adopted to filter noises in the retrieved SSCs. Figure 9e presents the spatial distributions of the estimated SSCs in the water area. The SSCs vary from 79 mg/L to 146 mg/L.

4. Discussion

4.1. Reference Surface Height

The reference surface height is the basis of the 3D point-cloud method. Only when the reference surface is obtained can the NWSP and the range bias of green laser be calculated. In an ALB system that emits IR and green lasers, the surface height of IR laser can be used as a reference.

As shown in Figure 9a, systematical height differences exist in the strip overlap area. The height difference in the strip overlap area is mainly induced by the tide. During the ALB measurements, the surface height derived by ALB shows a trend with a 43 cm drop and that derived by the tide tables with a 38 cm drop. The variation of surface height derived by the ALB is in accordance with that derived by the tide table. Due to the green and IR lasers that are collinearly and simultaneously emitted in CZMIL system, the tide has no influence on the 3D point-cloud method. For other ALB systems, reference surface height can be obtained by external methods, such as GPS measurement or leveling.

4.2. SSC Sampling Stations

In the proposed method, SSC field measurements should be performed to determine SSC for the establishment of a C-ΔS model. To ensure the accuracy of the model, the density and representativeness of SSC sampling stations should be considered by referring to the scope and turbidity variations in the water area [15]. To allow assessment of absolute accuracy, SSC measurements which are not used for calibration are necessary.

4.3. Applicability

(a) Water Surface

The slope and exposition of the water surface (wave front) play a role in the range bias of green laser. Assuming a sufficiently horizontal water surface, the range bias is a proxy for turbidity. But as soon as specular reflection from the water surface comes into play, the range bias is no longer directly connected to turbidity. Therefore, the proposed method is limited to calm waters.

(b) Water Quality

Generally, water quality can be divided into cases I and II [1]. Case I is dominated by phytoplankton (e.g., open oceans), and case II is dominated by suspended sediments (e.g., coastal and inland waters) [1]. The present study, which was carried out in coastal waters with case II, was based on the assumption that the absorption and scattering properties of the water are determined by suspended sediments, with no significant contribution from phytoplankton.

Figure 8 shows that the retrieving precision of the proposed method in high-turbidity domain is lower than that in low-turbidity domain. The problem can be explained by Figure 7, where ΔS increases with SSC, but the significant degree of the increase in high-turbidity domain is slightly less than that in low-turbidity domain. The phenomenon indicates that the proposed method may become lowly accurate in waters with considerably high turbidity.

5. Conclusions and Suggestions

This study proposed a novel 3D point-cloud method for fast remote sensing of sub-surface SSCs in calm waters by establishing an empirical relationship model between the measured SSCs and the range bias of the green surface points of ALB. The standard deviations of the SSCs retrieved by the 3D point-cloud method are less than 20 mg/L. The 3D point-cloud method is simpler, faster, and more convenient for application than that of traditional waveform method despite its lower precision. This method can be used as an alternative to the waveform method for remote sensing of sub-surface SSCs in calm waters when the accuracy requirement of SSC is low, and/or the waveform data are unavailable. The method may not be the best way to obtain SSCs with airborne LiDAR, but it is a way to potentially obtain additional information during bathymetric surveys.

The experiment was conducted in shallow and turbid waters with four SSC sampling stations for calibration. Further tests should be performed in similar waters with more SSC sampling stations. The reference surface height is the basis of the 3D point-cloud method and can be obtained by using external methods, such as IR laser, GPS measurement, or leveling. To ensure the effectiveness of 3D point-cloud method, it must be carried out in calm waters with no significant specular reflections.