Hyperspectral Measurement of Seasonal Variation in the Coverage and Impacts of an Invasive Grass in an Experimental Setting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Canopy Reflectance Measurements
2.2. Measurements of Vegetation Characteristics
2.3. Data Analysis
2.4. Model Evaluation
3. Results
3.1. Vegetation Characteristics
3.2. Using Spectral Reflectance to Predict Vegetation Characteristics
4. Discussion
4.1. Hyperspectral Prediction of Cogongrass Coverage
4.2. Hyperspectral Prediction of Dead Plant Coverage
4.3. Hyperspectral Detection of Canopy Water Content
4.4. Use of Spectral Data in Experimental Settings—Opportunities and Challenges
4.5. Landscape Scale Detection of Invasive Species
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brook, R.M. Review of literature on Imperata cylindrica (L.) Raeuschel with particular reference to South East Asia. Int. J. Pest Manag. 1989, 35, 12–25. [Google Scholar]
- Martin, H.; Petr, P.; Vojtěch, J. Impact of invasive plants on the species richness, diversity and composition of invaded communities. J. Ecol. 2009, 97, 393–403. [Google Scholar] [CrossRef]
- Barnes, T.G.; DeMaso, S.J.; Bahm, M.A. The Impact of 3 exotic, invasive grasses in the Southeastern United States on wildlife. Wildland Soc. Bull. 2013, 37, 497–502. [Google Scholar] [CrossRef]
- Davies, K.W.; Nafus, A.M. Exotic annual grass invasion alters fuel amounts, continuity and moisture content. Int. J. Wildland Fire 2013, 22, 353–358. [Google Scholar] [CrossRef]
- Shaw, D.R. Translation of remote sensing data into weed management decisions. Weed Sci. 2005, 53, 264–273. [Google Scholar] [CrossRef]
- He, K.S.; Rocchini, D.; Neteler, M.; Nagendra, H. Benefits of hyperspectral remote sensing for tracking plant invasions. Div. Distrib. 2011, 17, 381–392. [Google Scholar] [CrossRef]
- Peterson, E.B. Estimating cover of an invasive grass (Bromus tectorum) using tobit regression and phenology derived from two dates of Landsat ETM+ data. Int. J. Remote Sens. 2005, 26, 2491–2507. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive species detection in Hawaiian rainforests using airborne imaging spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
- Richardson, A.D.; Braswell, B.H.; Hollinger, D.Y.; Jenkins, J.P.; Ollinger, S.V. Near-surface remote sensing of spatial and temporal variation in canopy phenology. Ecol. Appl. 2009, 19, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Vitousek, P.M. Remote analysis of biological invasion and biogeochemical change. Proc. Natl. Acad. Sci. USA 2005, 102, 4383–4386. [Google Scholar] [CrossRef] [PubMed]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Huang, C.; Asner, G.P. Applications of Remote Sensing to Alien Invasive Plant Studies. Sensors 2009, 9, 4869–4889. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, K.S.; Skidmore, A.K. Spectral discrimination of vegetation types in a coastal wetland. Remote Sens. Environ. 2003, 85, 92–108. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- Underwood, E.; Ustin, S.; DiPietro, D. Mapping nonnative plants using hyperspectral imagery. Remote Sens. Environ. 2003, 86, 150–161. [Google Scholar] [CrossRef]
- Hunt, E.R.; McMurtrey, J.E.; Parker Williams, A.E.; Corp, L.A. Spectral characteristics of leafy spurge (Euphorbia esula) leaves and flower bracts. Weed Sci. 2004, 52, 492–497. [Google Scholar] [CrossRef]
- Hestir, E.L.; Khanna, S.; Andrew, M.E.; Santos, M.J.; Viers, J.H.; Greenberg, J.A.; Rajapakse, S.S.; Ustin, S.L. Identification of invasive vegetation using hyperspectral remote sensing in the California Delta ecosystem. Remote Sens. Environ. 2008, 112, 4034–4047. [Google Scholar] [CrossRef]
- Varga, T.A.; Asner, G.P. Hyperspectral and lidar remote sensing of fire fuels in hawaii volcanoes national park. Ecol. Appl. 2008, 18, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Olsson, A.D.; van Leeuwen, W.J.D.; Marsh, S.E. Feasibility of Invasive Grass Detection in a Desertscrub Community Using Hyperspectral Field Measurements and Landsat TM Imagery. Remote Sens. 2011, 3, 2283–2304. [Google Scholar] [CrossRef]
- Ishii, J.; Washitani, I. Early detection of the invasive alien plant Solidago altissima in moist tall grassland using hyperspectral imagery. Int. J. Remote Sens. 2013, 34, 5926–5936. [Google Scholar] [CrossRef]
- Barbosa, J.M.; Asner, G.P.; Martin, R.E.; Baldeck, C.A.; Hughes, F.; Johnson, T. Determining Subcanopy Psidium cattleianum Invasion in Hawaiian Forests Using Imaging Spectroscopy. Remote Sens. 2016, 8, 33. [Google Scholar] [CrossRef]
- Noujdina, N.V.; Ustin, S.L. Mapping Downy Brome (Bromus tectorum) Using Multidate AVIRIS Data. Weed Sci. 2008, 56, 173–179. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Wu, J.; Zhao, K.; Serbin, S.; Lee, J.-E. Seasonal variability of multiple leaf traits captured by leaf spectroscopy at two temperate deciduous forests. Remote Sens. Environ. 2016, 179, 1–12. [Google Scholar] [CrossRef]
- Dozier, H.; Gaffney, J.F.; McDonald, S.K.; Johnson, E.R.R.L.; Shilling, D.G. Cogongrass in the United States: History, Ecology, Impacts, and Management. Weed Technol. 1998, 12, 737–743. [Google Scholar] [CrossRef]
- Lippincott, C.L. Ecological consequences of Imperata cylindrica (cogongrass) invasion in Florida sandhill. Doctoral Dissertation, University of Florida, Gainesville, FL, USA, 1997. [Google Scholar]
- Brewer, S. Declines in plant species richness and endemic plant species in longleaf pine savannas invaded by Imperata cylindrica. Biol. Invasions 2008, 10, 1257–1264. [Google Scholar] [CrossRef]
- MacDonald, G.E. Cogongrass (Imperata cylindrical)—Biology, ecology, and management. Crit. Rev. Plant Sci. 2004, 23, 367–380. [Google Scholar] [CrossRef]
- Tominaga, T. Seasonal change in the standing crop of Imperata cylindrical var. koenigii grassland in the Kii-Oshima Island of Japan. Weed Res. Jpn. 1989, 34, 127–132. [Google Scholar]
- Estrada, J.A.; Flory, S.L. Cogongrass (Imperata cylindrica) invasions in the US: Mechanisms, impacts, and threats to biodiversity. Glob. Ecol. Conserv. 2015, 3, 1–10. [Google Scholar] [CrossRef]
- Lippincott, C.L. Effects of Imperata cylindrical (L.) Beauv. (Cogongrass) Invasion on Fire Regime in Florida Sandhill (USA). Nat. Areas J. 2000, 20, 140–149. [Google Scholar]
- King, S.E.; Grace, J.B. The effects of gap size and disturbance type on invasion of wet pine savanna by cogongrass, Imperata cylindrica (Poaceae). Am. J. Bot. 2000, 87, 1279–1286. [Google Scholar] [CrossRef] [PubMed]
- Mathur, A.; Bruce, L.M.; Byrd, J. Discrimination of subtly different vegetative species via hyperspectral data. In Proceedings of the IEEE International on Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 2, pp. 805–807. [Google Scholar]
- Huang, Y.; Bruce, L.M.; Byrd, J.; Mask, B. Using wavelet transform of hyperspectral reflectance curves for automated monitoring of Imperata cylindrica (cogongrass). In Proceedings of the IEEE 2001 International on Geoscience and Remote Sensing Symposium (Cat. No.01CH37217, Sydney, NSW, Australia, 9–13 July 2001; Volume 5, pp. 2244–2246. [Google Scholar]
- Peet, R.K.; Allard, D.J. Longleaf pine vegetation of the southern Atlantic and eastern Gulf Coast regions: A preliminary classification. In Proceedings of the Tall Timbers Fire Ecology Conference; Tall Timbers Research Station: Tallahassee, FL, USA, 1993; Volume 18, pp. 45–81. [Google Scholar]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Heumann, B.W.; Hackett, R.A.; Monfils, A.K. Testing the spectral diversity hypothesis using spectroscopy data in a simulated wetland community. Ecol. Inform. 2015, 25, 29–34. [Google Scholar] [CrossRef]
- Alba, C.; NeSmith, J.E.; Fahey, C.; Angelini, C.; Flory, S.L. Methods to test the interactive effects of drought and plant invasion on ecosystem structure and function using complementary common garden and field experiments. Ecol. Evol. 2017, 7, 1442–1452. [Google Scholar] [CrossRef] [PubMed]
- Underwood, E.C.; Mulitsch, M.J.; Greenberg, J.A.; Whiting, M.L.; Ustin, S.L.; Kefauver, S.C. Mapping Invasive Aquatic Vegetation in the Sacramento-San Joaquin Delta using Hyperspectral Imagery. Environ. Monit. Assess. 2006, 121, 47–64. [Google Scholar] [CrossRef] [PubMed]
- Fahey, C.; Angellini, C.; Flory, S. Grass invasion and drought interact to alter the diversity and structure of native plant communities. 2018; in press. [Google Scholar]
- Danson, F.M.; Steven, M.D.; Malthus, T.J.; Clark, J.A. High-spectral resolution data for determining leaf water content. Int. J. Remote Sens. 1992, 13, 461–470. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons using rank sums. Technometrics 1964, 6, 241–252. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Miles, J. R Squared, Adjusted R Squared. Wiley StatsRef Stat. Ref. Online 2014. [Google Scholar] [CrossRef]
- RS Team. RStudio: Integrated Development for R; RStudio Inc.: Boston, MA, USA, 2015. [Google Scholar]
- Wehrens, R.; Mevik, B.H. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–24. [Google Scholar]
- Stevens, A.; Ramirez–Lopez, L. An Introduction to the Prospectr Package. Available online: ftp://200.236.31.2/CRAN/web/packages/prospectr/vignettes/prospectr-intro.pdf (accessed on 14 February 2014).
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Klemas, V.; Smart, M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of. Spartina Alterniflora 1983, 49, 77–83. [Google Scholar]
- Rouse, J., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS; NASA: College Station, TX, USA, 1974; Volume 1, pp. 309–317. [Google Scholar]
- Fajardo, A.; Siefert, A. Phenological variation of leaf functional traits within species. Oecologia 2016, 180, 951–959. [Google Scholar] [CrossRef] [PubMed]
- Ichoku, C.; Karnieli, A. A review of mixture modeling techniques for sub-pixel land cover estimation. Remote Sens. Rev. 1996, 13, 161–186. [Google Scholar] [CrossRef]
- Daneshgar, P.; Jose, S.; Collins, A.; Ramsey, C. Cogongrass (Imperata cylindrica), an alien invasive grass, reduces survival and productivity of an establishing pine forest. For. Sci. 2008, 54, 579–587. [Google Scholar]
- Roberts, D.A.; Smith, M.O.; Adams, J.B. Green vegetation, nonphotosynthetic vegetation, and soils in AVIRIS data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO-1 Hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]
- Mutlu, M.; Popescu, S.C.; Zhao, K. Sensitivity analysis of fire behavior modeling with LIDAR-derived surface fuel maps. For. Ecol. Manag. 2008, 256, 289–294. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Dimitrakopoulos, A.P. Conversion of fuel moisture content values to ignition potential for integrated fire danger assessment. Can. J. For. Res. 2004, 34, 2284–2293. [Google Scholar] [CrossRef]
- Okin, G.S. Relative spectral mixture analysis—A multitemporal index of total vegetation cover. Remote Sens. Environ. 2007, 106, 467–479. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Peñuelas, J. Deriving Water Content of Chaparral Vegetation from AVIRIS Data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Ustin, S.L.; Riaño, D.; Vanderbilt, V.C. Water content estimation from hyperspectral images and MODIS indexes in Southeastern Arizona. Remote Sens. Environ. 2008, 112, 363–374. [Google Scholar] [CrossRef]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ. 2008, 112, 1820–1834. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Hunt, E.R.; Jackson, T.J. Remote sensing of vegetation water content from equivalent water thickness using satellite imagery. Remote Sens. Environ. 2008, 112, 2514–2522. [Google Scholar] [CrossRef]
- Price, J.C.; Bausch, W.C. Leaf area index estimation from visible and near-infrared reflectance data. Remote Sens. Environ. 1995, 52, 55–65. [Google Scholar] [CrossRef]
- Asner, G.P.; Nepstad, D.; Cardinot, G.; Ray, D. Drought stress and carbon uptake in an Amazon forest measured with spaceborne imaging spectroscopy. Proc. Natl. Acad. Sci. USA 2004, 101, 6039–6044. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Dvorák, P.; Müllerová, J.; Bartalos, T.; Bruna, J. Unmanned Aerial Vehicles for Alien Plant Species Detection and Monitoring. In The International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Göttingen, Germany, 2015; Volume XL, pp. 83–90. [Google Scholar]
- Hill, D.J.; Tarasoff, C.; Whitworth, G.E.; Baron, J.; Bradshaw, J.L.; Church, J.S. Utility of unmanned aerial vehicles for mapping invasive plant species: A case study on yellow flag iris (Iris pseudacorus L.). Int. J. Remote Sens. 2017, 38, 2083–2105. [Google Scholar] [CrossRef]




| Training Data | Test Data | Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Season (Date) | Sample Size | Season (Date) | Sample Size | NL | R2 (C) | RMSE (C) | (P) | RMSE (P) | |
| Same Season | wet (6/2015) | 54 | wet (6/2016) | 10 | 7 | 0.88 | 0.09 | −0.88 | 0.42 |
| dry (2/2016 + 12/2016) | 57 | dry (3/2017) | 16 | 4 | 0.85 | 0.14 | 0.41 | 0.13 | |
| Different Season | wet (6/2015 + 6/2016) | 56 | dry (2/2016 + 12/2016 + 3/2017) | 28 | 11 | 0.89 | 0.09 | −6.59 | 0.8 |
| dry (2/2016 + 12/2016 + 3/2017) | 56 | wet (6/2015 + 6/2016) | 28 | 10 | 0.93 | 0.08 | −1.80 | 0.5 | |
| All Seasons Together | wet and dry (6/2015 + 2/2016 + 6/2016 + 12/2016 + 3/2017) | 91 | wet and dry (6/2015 + 2/2016 + 6/2016 + 12/2016 + 3/2017) | 46 | 11 | 0.83 | 0.12 | 0.68 | 0.21 |
| Training Data | Test Data | Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Season (Date) | Sample Size | Season (Date) | Sample Size | NL | R2 (C) | RMSE (C) | (P) | RMSE (P) | |
| Same Season | wet (6/2015) | 54 | wet (6/2016) | 10 | 7 | 0.91 | 0.09 | −1.21 | 0.34 |
| dry (2/2016 + 12/2016) | 57 | dry (3/2017) | 16 | 4 | 0.79 | 0.14 | 0.43 | 0.11 | |
| Different Season | wet (6/2015 + 6/2016) | 56 | dry (2/2016 + 12/2016 + 3/2017) | 28 | 9 | 0.87 | 0.1 | −2.27 | 0.49 |
| dry (2/2016 + 12/2016 + 3/2017) | 56 | wet (6/2015 + 6/2016) | 28 | 9 | 0.91 | 0.09 | 0.61 | 0.17 | |
| All Seasons Together | wet and dry (6/2015 + 2/2016 + 6/2016 + 12/2016 + 3/2017) | 91 | wet and dry (6/2015 + 2/2016 + 6/2016 + 12/2016 + 3/2017) | 46 | 9 | 0.87 | 0.11 | 0.57 | 0.16 |
| Vegetation Characteristic | NL | R2 (C) | RMSE (C) | RE (C) | R2 (CV) | RMSE (CV) | RE (CV) | (P) | RMSE (P) | RE (P) |
|---|---|---|---|---|---|---|---|---|---|---|
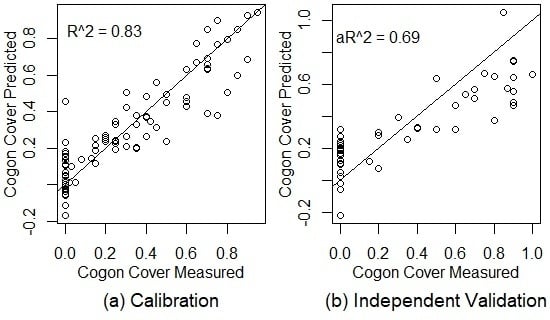
| Cogon Cover | 11 | 0.83 | 0.123 | 39.78% | 0.65 | 0.196 | 59.50% | 0.69 | 0.206 | 55.99% |
| Dead Plant | 9 | 0.87 | 0.105 | 20.91% | 0.74 | 0.151 | 35.49% | 0.57 | 0.155 | 57.01% |
| L/D Ratio | 3 | 0.23 | 1.095 | 111.64% | 0.10 | 1.048 | 107.81% | −0.08 | 0.712 | 74.45% |
| Canopy EWT | 5 | 0.45 | 0.025 | 43.75% | 0.28 | 0.032 | 51.22% | 0.33 | 0.033 | 44.94% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Graves, S.; Flory, S.L.; Bohlman, S. Hyperspectral Measurement of Seasonal Variation in the Coverage and Impacts of an Invasive Grass in an Experimental Setting. Remote Sens. 2018, 10, 784. https://doi.org/10.3390/rs10050784
Guo Y, Graves S, Flory SL, Bohlman S. Hyperspectral Measurement of Seasonal Variation in the Coverage and Impacts of an Invasive Grass in an Experimental Setting. Remote Sensing. 2018; 10(5):784. https://doi.org/10.3390/rs10050784
Chicago/Turabian StyleGuo, Yuxi, Sarah Graves, S. Luke Flory, and Stephanie Bohlman. 2018. "Hyperspectral Measurement of Seasonal Variation in the Coverage and Impacts of an Invasive Grass in an Experimental Setting" Remote Sensing 10, no. 5: 784. https://doi.org/10.3390/rs10050784
APA StyleGuo, Y., Graves, S., Flory, S. L., & Bohlman, S. (2018). Hyperspectral Measurement of Seasonal Variation in the Coverage and Impacts of an Invasive Grass in an Experimental Setting. Remote Sensing, 10(5), 784. https://doi.org/10.3390/rs10050784