1. Introduction
Hyperspectral imaging has become an emerging technique in remote sensing and has been successfully used in many applications, such as military reconnaissance, mineral exploration, and environmental monitoring [
1]. Hyperspectral images (HSIs) record both the spatial and spectral information of a scene, and they can provide especially high spectral resolution with hundreds of narrow bands that enable precise material identification [
2]. However, HSIs often suffer from low spatial resolution, which means that one pixel may contain more than one material; in other words, there are mixed pixels. To address this problem, the spectral information can be utilized to identify the spectrum of each material (called endmember) in the mixed pixels and their corresponding percentages (called abundance); the whole procedure is called unmixing. As a result of the widely existing mixed pixels in HSIs and in order to make full use of the data, it is important to develop efficient unmixing algorithms for HSI analysis.
There are two main categories of models for hyperspectral unmixing (HU), namely, the linear mixing model (LMM) and the nonlinear mixing model [
3]. As a result of the model simplicity and good result interpretability, LMM-based approaches are predominant in the HU literature. Under the LMM, each mixed pixel is considered as a linear combination of endmember signatures that is weighted by the corresponding abundances. In addition, there are two constraints in the LMM that are used to obtain a physical meaning result, namely, the abundance nonnegative constraint (ANC) and the abundance sum-to-one constraint (ASC).
In the last decade, a large number of algorithms have been designed based on the LMM for HU [
4]. These algorithms can be mainly divided into three categories, namely, geometrical, sparse regression based, and statistical. The geometrical unmixing algorithms are based on the fact that, under the LMM, the feature vectors of the pixels in HSI are all included in a simplex, and the vertices of the simplex are supposed as the endmembers. Some of the geometric based methods assume that pure pixels always exit in HSI, and the task of these algorithms is to search for these pure pixels as endmembers, including the pixel purity index [
5], N-FINDER [
6], automated morphological endmember extraction [
7], vertex component analysis (VCA) [
8], and the simplex growing algorithm [
9]. Others do not depend on the pure pixel assumption and seek a minimum volume simplex that encloses the data set—for example, minimum volume enclosing simplex [
10], simplex identification via variable splitting and augmented Lagrangian [
11], and minimum volume simplex analysis [
12]. Most of the geometric-based algorithms can only extract the endmembers. Hence, some abundance estimation algorithms are needed, such as the fully constrained least squares (FCLS) [
13] and simplex projection unmixing [
14]. The sparse regression-based algorithms work in a semi-supervised way, utilizing the ground spectral libraries so as to perform HU. An advantage of these approaches is that they evade the endmember extraction step and do not require the presence of pure pixels in the scene. However, they suffer from the large size of the spectral libraries and the difference between the ground library and the real measured data. The statistical approaches analyse the mixed pixels by exploiting the inner statistical rules in the data. These kinds of methods have been proven to be able to unmix highly mixed data and obtain a higher decomposition accuracy, despite the relatively high computation complexity. The representative algorithms of the statistical methods include the independent component analysis (ICA) [
15,
16], nonnegative matrix/tensor factorization (NMF/NTF) [
17,
18], and Bayesian approaches [
19].
NMF focuses on the decomposition of a nonnegative matrix into two factors that are also nonnegative [
20,
21]. The non-negativity constraint makes the NMF-based algorithms particularly attractive, which allows for better interpretability. NMF-based algorithms have been successfully used over a variety of areas, such as document clustering, face recognition, blind audio source separation, and more. NMF has also shown great potential in HU. NMF-based unmixing algorithms estimate endmembers and abundances simultaneously and they satisfy the ANC in LMM naturally. However, the NMF problem is non-convex, and there are many local minima in the solution space. To alleviate this situation, extra auxiliary constraints are added upon the endmembers and abundances. Miao and Qi have proposed the minimum volume constrained NMF [
22], which regulates the simplex volume that has been determined by the endmembers to be small. A similar idea is also adopted in the iterated constrained endmembers [
23] and robust collaborative NMF [
24], which replace the minimum volume constraint with a convex and simple surrogate. Huck introduced a regularizer that forces the endmember spectral variance to be low and thus encourages the flat endmember spectral, and proposed minimum dispersion constrained NMF [
25]. The endmember dissimilarity constrained NMF [
26] combines NMF with the endmember dissimilarity constraint, which can impose both a minimum volume and smoothing effects on endmembers.
The abundance constraints are also added into the NMF model in order to obtain a more accurate solution for HU. The sparsity of the abundance matrix is often considered under the fact that most of the pixels in HSI are mixed by only a subset of endmembers, rather than by all of the endmembers [
27]. For example, the piecewise smoothness NMF with sparseness constraint [
28], which was proposed by Jia and Qian, incorporates both the abundance smoothness and sparseness constraints into the NMF. Then, Qian et al. introduced the
regularizer so as to enforce the sparsity of the abundances, and proposed the
-NMF [
29]. They demonstrated that the
regularizer is a better choice because the ASC constraint and the
regularizer are in conflict. The sparsity increases as
decreases for
(
), whereas the sparsity is not obviously improved as
continues to reduce for
(
). They also showed that the
regularizer is closely linked to the minimum volume method, because when the volume of the simplex becomes larger, the sparse degree of the abundances becomes lower. Recently, some researchers have incorporated spatial information with the sparseness constraint. Zhu et al. has proposed a data-guided sparse method, in which the value of
for each pixel is determined by a learned data-guided map in order to adaptively impose the sparseness constraint [
30]. A similar idea was adopted by Wang et al., as they incorporated a spatial group sparseness constraint into NMF for HU, which supposes that the pixels within a local spatial group share the same sparse structure [
31].
The special information of the abundances is also a frequently exploited property in the literature for HU [
32]. The ground objects usually change slowly, and each ground object often exists in a specific area of the whole scene. Based on these two facts, Liu et al. has proposed an approach that is named the abundance separation and smoothness constrained NMF (ASSNMF) [
33], which imposes the abundance separation and smoothness constraints on NMF. Similarly, the total variation regularizer is introduced so as to promote the piecewise smoothness of the abundances in [
34]. Moreover, some of the algorithms attempt to utilize the internal structural information of HSI and suppose that similar pixels correspond to similar abundances, such as graph-regularized
-NMF (GLNMF) [
35], structured sparse NMF (SS-NMF) [
36], and hypergraph-regularized
-NMF (HG
-NMF) [
37], which are all based on the graph Laplacian constraint [
38]. In [
39] and [
40], however, the structural information is adopted by clustering and region segmentation, and the mean abundance of each class or region is computed so as to keep the abundance vectors similar.
In the existing unmixing algorithms, the abundance spatial or structural constraints are often used in conjunction with the sparsity constraints. In the commonly used sparsity constraints, the
sparse constraint is no longer suitable when the ASC condition is needed, whereas the
sparse constraint will introduce an additional local minima as a result of non-convexity, thereby reducing the algorithm convergence rate, and making it sensitive to noise. In most of the algorithms, the spatial and structural information are usually considered separately, so the correlation between the pixels is not fully utilized. In this paper, a new unmixing method, named the bilateral filter regularized
sparse NMF (BF-
SNMF), is proposed for HU. Two abundance constraints are added onto NMF. Firstly, the
sparse constraint is proposed, which considers the sparseness of the abundance vectors. It can work when the ASC is satisfied, and has the attractive mathematical characteristics of simplicity and being Lipschitz continuous. Secondly, in order to make full use of the correlation between pixels in HSI, a graph constraint that is based on the bilateral filter is introduced. It considers the spatial information and the manifold structure features of the abundance maps together, which can effectively improve the accuracy of the endmember and abundance estimation. To improve the algorithm convergence rate, we used NeNMF to minimize the object function [
41]. The main contributions of the paper are summarized as follows:
The sparse constraint is incorporated into the NMF model so as to improve the sparsity of the abundance vectors. In the case of satisfying the ASC condition, the sparse constraint can explore the sparse property of the abundance more effectively.
The bilateral filter regularizer is introduced so as to utilize the correlation information between the abundance vectors. By considering both the spatial and spectral distances between the pixels, the bilateral filter constraint can make the algorithm more adaptive to the regions that contain edges and complex texture.
The remainder of this paper consists of the following. In
Section 2, the LMM and the NMF algorithm are briefly introduced. The proposed BF-
SNMF model and its corresponding optimization solution are described in detail in
Section 3.
Section 4 presents and analyses the simulated and real data experiments for unmixing, using the BF-
SNMF algorithm. Lastly, the discussions and conclusions are drawn in
Section 5 and
Section 6.
3. Proposed Bilateral Filter Regularized Sparse NMF Method
As a result of the non-convexity of the NMF model, a lot of local minima existed in the solution space, so the optimization algorithm may have converged to a local optimum and the results were not unique for the different initializations. For example, given one solution of and , there existed a set of solutions, and , which had the same reconstruction error, where could be any nonnegative invertible matrix. In order to shrink the solution space, some effective constraints that reflected the intrinsic properties of HSI were usually added onto the NMF model. As we know, a pixel of HSI was usually composed by a small subset of the endmembers, so the abundance was often supposed to be sparse. Moreover, the correlation of the neighboring pixels was also reflected in abundance. In this paper, we proposed a NMF-based method, which combined the sparsity and correlation information of the abundance maps for HU.
3.1. Sparse Prior
Since most of the pixels were composed by only one or a few endmembers, but not all of the endmembers, the abundance vector of a pixel in HSI was usually assumed to be sparse. In other words, there were many zero entries in the abundance vector, and most of the entries of the abundance matrix were also supposed to be zero. Many solutions were proposed in order to exploit the abundance sparse property in recent years. The typical solution used the
-norm regularizer by counting the nonzero elements in the abundance matrix. However, solving the
-norm regularizer was an NP-hard problem, and the
-norm regularizer was widely used as an alternative method. Although the
-norm term could give a sparse solution in most cases, it could no longer play a role when the ASC was considered during the unmixing. Then, other alternative regularizers, such as the
(
)-norm regularizer and especially the
-norm one, were proposed. The
(
)-norm minimization problem could be expressed as follows:
Some additional techniques were introduced to further utilize the sparsity of the abundances more subtly, such as the data-guided sparsity [
30], reweighted
-norm regularizer [
34], and the arctan sparse constraint [
44]. In this paper, we considered the ASC and the sparse constraint together, and proposed to use the
-norm in order to enhance the sparsity of the abundances in the NMF model.
We found that when the ASC condition was added, the larger the
-norm of a pixel abundance vector, the sparser the abundance vector. For example, if there were two solutions
and
, the sparser solution
had a larger
-norm value. The
-norm maximization problem could be summarized as follows:
where
represents the
-norm of the vector. The
sparse constraint had the advantages of simplicity and being Lipschitz continuous. It could get a relatively good sparse effect. The sparsity of the
-norm under the ASC condition could be demonstrated by the following derivation. Assuming
, and
met the ASC condition, that is
, and taking
into
, we get:
Considering the sparseness of
at
, we get the partial derivative of
to
, as follows:
Since
, so
, if, and only if,
, the two sides were equal. Therefore, the
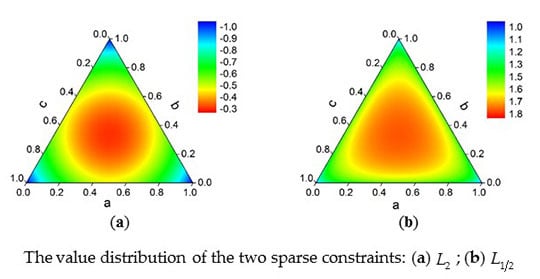
-norm could have produced a certain sparse effect under the ASC condition. We plotted the value of
as a triangle graph under the ASC condition, and we also plotted the function value of the
constraint, which is
, as a comparison. As shown in
Figure 1.
From
Figure 1 we can see that as the sparsity of the abundance vector increased, the value of the
sparse constraint decreased more uniformly than the
constraint, which had a relatively big change, only when the sparsity was large. According to the analysis above, the
sparse constraint was defined as follows:
After adding the
sparse constraint onto the NMF model, the new object function was shown in Equation (12), which we called
sparse NMF (
SNMF).
In fact, similar to , the norm () could also make a sparse effect in the same way. In this paper, only the situation when has been discussed.
3.2. Bilateral Filter Regularizer
The sparse constraint only considered the abundance characteristics of a single pixel. However, the pixels in HSI had correlations in both the spatial and spectral space. These correlations could have resulted in the similarities between some of the neighboring abundance vectors. Therefore, fully exploiting these correlations would have effectively improved the accuracy of the unmixing. When considering the correlation of the pixels in the spatial space, it was generally considered that the spatially adjacent pixels had similar abundance vectors, that is, the abundance map was smooth. Some algorithms were based on this assumption, such as ASSNMF. When considering the pixel correlation in the spectral space, the pixels with similar spectral features were considered to have similar abundance vectors, that is, the abundance vector data set maintained the manifold structure of the spectral feature data set. The algorithms that were based on this assumption included the GLNMF, SS-NMF, and HG -NMF. Inspired by the bilateral filter, we considered the correlations of the pixels in both the spatial and spectral space, and proposed a new regularizer that was based on the graph theory for hyperspectral unmixing, which we called the bilateral filter regularizer.
The bilateral filter was a simple and effective edge-preserving filter [
45]. It took into account both the spatial and spectral similarity between pixels, and gave large weights to the pixels that were both spatially and spectrally similar. In the bilateral filter regularizer, we adopted a similar rule and supposed that the abundance vectors that corresponded to the pixels, which were both spatially and spectrally similar, had a higher degree of similarity. Given an HSI
, and considering each pixel in
as a node, the correlation weights between the different nodes could be learned as follows:
where
represents the spatial distance between the
i-th and the
j-th pixels. We used the Euclidean distance.
is the distance diffusion parameter,
is the feature diffusion parameter, and
is the joint similarity measure. Obviously, the larger the
, the smaller the effect of the spatial distance on
, and the larger the
, the smaller the effect of the spectral distance on
, and a large
value suggests that the two pixels were similar. To better adapt to the edge area and the area where the features changed greatly, and to reduce the amount of computation, we set a threshold
, and made
effective only when the value of
was greater than
, otherwise we set the weight to 0. In this paper, we set
to 0.1 (experience).
According to the process above, we could calculate the weight between any two pixels in the HSI and get the weight matrix
of size
. Under the previous assumption, similar pixels had similar abundance vectors. Using the
-norm as the measure of distance, the bilateral filter regularizer that could control the level of similarity between the abundance vectors was defined as follows:
where
represents the trace of the matrix,
is a diagonal matrix and
, and
is generally called the graph Laplacian matrix.
3.3. The BF- SNMF Unmixing Model
By integrating the bilateral filter regularizer into
SNMF Equation (12), the object function of the proposed BF-
SNMF could be expressed as follows:
In Equation (15), the first term was the reconstruction error, the second was used to enhance the sparseness of the abundance matrix, and the third was adopted to exploit the correlation between the abundance vectors.
There were two major improvements in BF- SNMF when compared with the other NMF-based unmixing algorithms. The first was the combination of the ASC constraint and the -norm so as to improve the sparsity of the abundance matrix. The second was the introduction of the bilateral filter regularizer that could better explore the pixel correlation information that was hidden in the HSI data.
3.4. Optimization Algorithm
Since both of the constraints in the BF-
SNMF were Lipschitz continuous, NeNMF could be used to optimize the model. NeNMF was proposed by Guan et al. [
41]. It used the Nesterov optimal gradient method to solve the NMF model, which had the advantage of a fast convergence rate, compared with the traditional multiplication iteration and the steepest gradient decent method. A strategy, named the alternating nonnegative least squares, was used to minimize the object function of Equation (15). For each iteration, one matrix was fixed, and the other was optimized, thus updating
and
alternately until convergence. We called this process the outer iteration. The first
outer iteration process was as follows:
When optimizing
, the alternating optimization method was also adopted in order to get the single optimal point. We called this process the inner iteration. According to the Nesterov optimal gradient method, which defined the auxiliary matrix
, the updating rules of
and
in the inner iteration could be expressed as follows:
where
is the union coefficient, and
sets the negative value in matrix
to 0, so that
satisfies the ANC.
is the Lipschitz constant with respect to
, and for any two matrices,
,
should make the inequality of Equation (20) hold. We take
as
here.
In this paper, the Karush–Kuhn–Tucker (KKT) conditions were used as the stopping criterion for the inner iteration. It was equal to the projection gradient of the object function to
, being 0. Since it was time consuming to completely converge to the extremely optimal point, we relaxed the stopping condition, and stopped the iteration when the F-norm of the projection gradient was less than a certain threshold, as follows:
where the threshold
was set as 1e-3 in our experiments, and
represents the projection gradient of the object function to
, which is defined as follows:
The whole process of optimizing
is shown in Algorithm 1.
| Algorithm 1 Optimal gradient method (OGM) |
Input:,
Output:
1: Initialize , , ,
repeat
2: Using Equation (16), update
3: Using Equation (17), update
4: Using Equation (18). update
5:
until Stopping criterion is satisfied
6: |
In Algorithm 1, the solution of
was similar to the method that was used in [
41], and
was the spectral norm of the matrix. The gradient of the object function to
is as follows:
For updating the matrix
, we used the same method as
, except for the gradient and the Lipschitz constant. The gradient of the object function to
is as follows:
The solution of the Lipschitz constant, with respect to
, is shown in Equation (25), where
. Since
may be a sparse matrix with large dimensions, it was difficult to solve the spectral norm. We used the F-norm instead.
Therefore, the Lipschitz constant
could be calculated as follows:
Using Algorithm 1 to optimize matrices and , we get the solution of BF- SNMF as Algorithm 2. We adopted the following stopping conditions for Algorithm 2, namely: (1) the number of iterations reached the maximum, and (2) the variation of the object function was less than a certain threshold for five continuous iterations. As long as one of the two conditions was satisfied, the iteration was terminated. In this paper, we set the maximum number of iterations to 200 and the stopping threshold to 1e-3.
To conveniently compare with other algorithms, we also provided the multiplication iteration method of
SNMF. According to the gradient descent algorithm, we got the updating rule of BF-
SNMF, as follows:
By setting
,
and
, we got the updating rule of
SNMF in multiplicative form, as follows:
| Algorithm 2 Bilateral Filter Regularized Sparse NMF (BF- SNMF) for HU |
Input: Hyperspectral data ; the number of endmembers ; the parameters , , ,
Output: Endmember matrix and abundance matrix
1: Initialize , , and
repeat
2: Update with
3: Update with
4:
until Stopping criterion is satisfied
5: , |
3.5. Implementation Issues
Since the BF- SNMF algorithm was still non-convex, different initializations and parameters may have led to quite different results. During the implementation, there were several issues that needed attention.
The first issue was the initialization of and . Since there were many local minima in the solution space, the initialization of and was very important. There were many endmember initialization methods that were often used, such as the random initialization, artificial selection, K-means clustering, and some fast geometric endmember extraction algorithms. For the initialization of abundance, the common methods included the random initialization, project Moor–Penrose inverse, and FCLS. In this paper, we used the VCA and FCLS to initialize and in the simulation and the Cuprite data experiments, and we used the K-means clustering and the project Moor–Penrose inverse as the initializations in the urban data experiment.
The second issue was the ASC constraint. Since the proposed
sparse constraint could produce the sparse effect only when the ASC condition was satisfied, the ASC constraint was necessary for the BF-
SNMF. In some cases, where the ASC constraint was not suitable, we could replace the
sparse constraint with the
-norm. We considered the ASC constraint in the same way as [
13]. When updating
during the iteration,
and
were replaced by
and
, which were defined as Equation (31). Where
controlled the strength of the constraint, in this paper, we set
to 20.
The third was the parameter determination. There were five parameters in BF-
SNMF. They were
,
,
,
, and
.
was the number of endmembers, we assumed that
was known in this paper. In practice, some endmember number estimation algorithms, such as VD (virtual dimensionality) [
46] or HySime [
47], could have been used.
and
were the penalty coefficients, the choice of these two parameters should have been related to the sparsity and textural complexity of the image. We analyzed the impact of the different parameters on the results, with experiments in
Section 4.
controlled the effective spatial range of the bilateral filter. We assumed that the area around pixel
, where pixel
satisfied
as the valid spatial area. If the valid window size was set as
, then the value of
should have been in the range of
. In this paper, we selected
as 1.5.
controlled the effective spectral range. We expected to include the noise range in the effective spectral range exactly and to exclude the normal texture change. Based on this idea, we set
as the standard deviation of the image noise, and used the SVD (singular value decomposition) [
48] method to estimate the noise.
3.6. Complexity Analysis
In this section, we analyzed the computational complexity of the BF-
SNMF algorithm. The most time-consuming step in BF-
SNMF was the calculation of
and
. Note that during the inner iteration,
,
, and the Lipschitz constant only needed to be calculated once. Since
was usually a sparse matrix, assuming the number of non-zero elements in
was
, then the multiplication operation times for calculating
were
. In addition,
only needed to be calculated once in the whole algorithm, so it could have been calculated in the initialization process.
Table 1 shows the number of multiplication operations in each iteration of BF-
SNMF and that of the original NMF for comparison. Where
and
represented the inner iteration numbers of
and
, respectively. Moreover, learning the weight matrix
in advance was needed. The traditional bilateral filter algorithm was time-consuming, but some acceleration algorithms could be utilized, such as the recursive bilateral filter [
49], whose computational complexity was
. For the whole algorithm procedure, assuming the number of outer iterations was
, the total computational complexity of NMF was
, whereas that of BF-
SNMF was
. For BF-
SNMF, because of the fast convergence rate of the inner iteration, which was
,
and
were generally small numbers. Therefore, the computational complexity of BF-
SNMF was at the same level as that of the original NMF algorithm. However, because the BF-
SNMF algorithm only required a few outer iterations, it consumed less time than the original NMF.
5. Discussion
In this study, the validity of the BF-
SNMF unmixing algorithm was investigated. The endmember signals and abundance maps that were estimated by the proposed BF-
SNMF algorithm fitted well with the references. It could be seen from experiments in
Section 4 that the performance of
SNMF improved obviously when compared with
-NMF. This demonstrated the advantage of the
sparse constraint. The performance difference between BF-
SNMF and
SNMF was also bigger than that between GLNMF and
-NMF. This indicated that the bilateral filter regularizer explored the correlation information between pixels more fully than the manifold regularizer in GLNMF. However, some improvements and issues need to be considered for further research.
Firstly, the BF-
SNMF imposed the same sparse constraint for all of the pixels in HSI. However, the mixing level of each pixel or region might have been different from each other. The spatial information could be incorporated with the
sparse constraint in order to achieve a more accuracy result. Similar to [
30] and [
31], a pixel-wise or region-smart
sparse constraint might be developed.
Secondly, there were usually some regularization parameters that were to be set for the NMF-based unmixing methods. It was hard work to always set them with optimal values for different images. Although this paper had qualitatively analyzed the influence of the parameter choice on the results, it was still difficult to automatically determine the best values of and . Therefore, a trade-off should have be made. How to determine a set of relatively feasible and values adaptively might be a direction in future research.
Thirdly, the generalization ability of the proposed method needed further verification. Although two representative HSI data were selected for the real experiments, it could not be ensured that the algorithm was applicable to any scenario. More HSI data should be used to verify the effectiveness of the algorithm. As a result of the small amount of the public HSI data and reference, it was difficult to have a comprehensive inspection of the generalization ability for the algorithm. With the increasing of the public data set for HU, this issue might be solved in the future.