The Generalized Gamma-DBN for High-Resolution SAR Image Classification
Abstract
:1. Introduction
- A generalized Gamma-Bernoulli RBM (gB-RBM) is proposed to learn the statistical model of high-resolution SAR images after casting it as a particular probability mixture model of the generalized Gamma distributions.
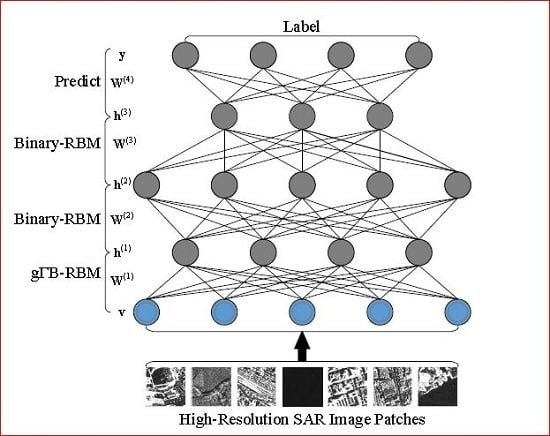
- By stacking the gB-RBM and several standard binary restricted Boltzmann machines, a generalized Gamma DBN (g-DBN) is constructed to learn high-level representations of different land-covers.
2. Materials and Methods
2.1. gB-RBM
| Algorithm 1K-CD for gB-RBM update for a mini-batch of size | |
| Input: A gB-RBM with m visual units and n hidden units and training batch S. | |
| Output: The gradient approximation of model parameter: , and , for and . | |
| 1: | Initialization: , and ; |
| 2: | for all do |
| 3: | ; |
| 4: | for to do |
| 5: | , sample ; |
| 6: | , sample ; |
| 7: | end for |
| 8: | for and do |
| 9: | Update : ; |
| 10: | Update : ; |
| 11: | Update : ; |
| 12: | end for |
| 13: | end for |
| 14: | return, and . |
2.2. Discriminant Classification via g-DBN
| Algorithm 2 Formulating a Discriminative Network (DisNet) | |
| Input: | |
| 1. Training SAR image samples: , where and ; | |
| 2. Number of units in each hidden layer: , , …, ; | |
| Output: A discriminative neural network . | |
| 1: | Initialization: ; |
| 2: | fortohdo |
| 3: | if then |
| 4: | Training a gB-RBM with input and hidden nodes. |
| 5: | Compute output of the 1st RBM ; |
| 6: | else |
| 7: | Training a stand binary RBM with input and hidden units. |
| 8: | Compute output of the ith RBM ; |
| 9: | end if |
| 10: | end for |
| 11: | Unfold the RBM series to a neural network ; |
| 12: | Add a prediction layer to with C output nodes: , where is initialized randomly; |
| 13: | Tune weights of the neural network with labels via a backpropagation procedure. |
| 14: | return. |
2.3. Discussions of the Proposed Approach
- After casting the proposed gB-RBM as a mixture model, the likelihood and model parameters can be effectively approximated via a simple gradient-based optimization (as shown in Algorithm 1). It needs less computation and easier to implement than traditional EM procedure in the probability mixture models.
- With a layer-by-layer representation, high-level representation can be generated by exploiting higher-order and nonlinear distributions of SAR images.
- As shown in Algorithm 2, the discriminative network is formulated by an unsupervised training of RBMs and supervised parameter tuning. It is easy to implement in a greedy and hierarchical manner.
3. Experimental Results and Discussions
- Patch Vector—Similar to the work of Varma et al. [56], a simple patch vector based descriptor is utilized as the basic feature to characterize SAR image samples. It just simply keeping the raw pixel intensities of a square neighborhood to form a feature vector.
- GLCM + Gabor [57]—In this experiment, some statistics of GLCM and responses of Gabor filters are employed to characterize SAR image samples. The statistics computed by the GLCM are energy, entropy, roughness, contrast and correlations. Meanwhile, the means and standard deviations of the magnitude of the Gabor filtering responses with 3-scales and 4-orientations are utilized in this experiment.
3.1. Performance Evaluation over Patch Sets
3.1.1. Datasets and Settings
3.1.2. Results and Analysis
3.2. Performance Evaluation over Large-Scale SAR Images
3.2.1. Barcelona Image
- Firstly, the Barcelona image is partitioned into 91,809 local patches in a non-overlapping manner, in which each one has 33 × 33 pixel in size. The patch set ptSet4 formulated in Table 2 are utilized for model training for all of these four approaches.
- The power parameter of the generalized Gamma distribution is setting as 2.
- In this experiment, a four layer DBN and g-DBN is trained for land-cover classification. It consists of one input layer, two hidden layer and one output layer. Specifically, the number of units of input layer is 1089, corresponding to each local patch. Meanwhile, the number of units in each hidden layer is setting as 200 and 20 respectively. The output layer has 4 nodes for different land-covers.
3.2.2. Napoli Image
- Firstly, the Napoli image is partitioned into 295,704 patches in a non-overlapping manner, in which each one has 9 × 9 pixels in size. At the same time, 30,000 local patches which are randomly captured from three marked areas (shown in Figure 10a) are employed to learn the g-DBN, in which 10,000 patches per each category.
- In this experiment, the power, i.e., , of gD (in Equation (1)) is also setting as 2.
- In this experiment, a three layer g-DBN is learned form the selected training samples. It has one hidden layer with 20 units. Numbers of units of the input and output layers are setting as 81 and 3 respectively, which are corresponding the input SAR image patch (9 × 9) and land-covers should be labeled.
3.3. Discussions
4. Conclusions and Further Works
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of Equations (4) and (5)
Appendix B. Calculation of the Equation (8)
References
- Liao, C.; Wang, J.; Shang, J.; Huang, X.; Liu, J.; Huffman, T. Sensitivity Study of Radarsat-2 Polarimetric SAR to Crop Height and Fractional Vegetation Cover of Corn and Wheat. Int. J. Remote Sens. 2018, 39, 1475–1490. [Google Scholar] [CrossRef]
- Tsyganskaya, V.; Martinis, S.; Marzahn, P.; Ludwig, R. SAR-based Detection of Flooded Vegetation—A Review of Characteristics and Approaches. Int. J. Remote Sens. 2018, 39, 2255–2293. [Google Scholar] [CrossRef]
- Montazeri, S.; Gisinger, C.; Eineder, M.; Zhu, X. Automatic Detection and Positioning of Ground Control Points Using TerraSAR-X Multiaspect Acquisitions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2613–2632. [Google Scholar] [CrossRef]
- Gohil, B.S.; Sikhakolli, R.; Gangwar, R.K.; Kumar, A.S.K. Oceanic Rain Flagging Using Radar Backscatter and Noise Measurements from Oceansat-2 Scatterometer. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2050–2055. [Google Scholar] [CrossRef]
- Li, H.C.; Krylov, V.A.; Fan, P.Z.; Zerubia, J.; Emery, W.J. Unsupervised Learning of Generalized Gamma Mixture Model With Application in Statistical Modeling of High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2153–2170. [Google Scholar] [CrossRef]
- Sportouche, H.; Nicolas, J.M.; Tupin, F. Mimic Capacity of Fisher and Generalized Gamma Distributions for High-Resolution SAR Image Statistical Modeling. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5695–5711. [Google Scholar] [CrossRef]
- Barreto, T.L.M.; Rosa, R.A.S.; Wimmer, C.; Moreira, J.R.; Bins, L.S.; augo Menocci Cappabianco, F.; Almeida, J. Classification of Detected Changes from Multitemporal High-Resolution X-band SAR Images: Intensity and Texture Descriptors from SuperPixels. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5436–5448. [Google Scholar] [CrossRef]
- Bahmanyar, R.; Cui, S.; Datcu, M. A Comparative Study of Bag-of-Words and Bag-of-Topics Models of EO Image Patches. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1357–1361. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Qiu, X.; Huang, Z.; Lei, B. Airplane Recognition in TerraSAR-X Images via Scatter Cluster Extraction and Reweighted Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 112–116. [Google Scholar] [CrossRef]
- Moser, G.; Zerubia, J.; Serpico, S.B. Dictionary-Based Stochastic Expectation-Maximization for SAR Amplitude Probability Density Function Estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 188–200. [Google Scholar] [CrossRef]
- Kayabol, K.; Voisin, A.; Zerubia, J. SAR Image Classification with Non-stationary Multinomial Logistic Mixture of Amplitude and Texture Densities. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 169–172. [Google Scholar]
- Peng, Q.; Zhao, L. SAR Image Filtering Based on the Cauchy–Rayleigh Mixture Model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 960–964. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Zhang, P.; Wu, Y.; Tan, X.; An, L. Mixture WG Γ-MRF Model for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 905–920. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Garcia, A.; Modolo, D.; Ferrari, V. Do Semantic Parts Emerge in Convolutional Neural Networks? Int. J. Comput. Vis. 2018, 126, 476–494. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraund, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Fan, J.; Wang, H.; Ma, X.; Li, B.; Chen, F. High-Resolution SAR Image Classification via Deep Convolutional Autoencoders. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2351–2355. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.Q. Target Classification Using the Deep Convolutional Networks for SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. Transfer Learning with Deep Convolutional Neural Network for SAR Target Classification with Limited Labeled Data. Remote Sens. 2017, 9, 907. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- De, S.; Bruzzone, L.; Bhattacharya, A.; Bovolo, F.; Chaudhuri, S. A Novel Technique Based on Deep Learning and a Synthetic Target Database for Classification of Urban Areas in PolSAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 154–170. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.; Doulamis, N.; Nikitakis, A.; Voulodimos, A. Tensor-based Nonlinear Classifier for High-Order Data Analysis. arXiv, 2018; arXiv:1802.05981. [Google Scholar]
- Qu, J.; Lei, J.; Li, Y.; Dong, W.; Zeng, Z.; Chen, D. Structure Tensor-Based Algorithm for Hyperspectral and Panchromatic Images Fusion. Remote Sens. 2018, 10, 373. [Google Scholar] [CrossRef]
- Huang, X.; Qiao, H.; Zhang, B.; Nie, X. Supervised Polarimetric SAR Image Classification Using Tensor Local Discriminant Embedding. IEEE Trans. Image Process. 2018, 27, 2966–2979. [Google Scholar] [CrossRef]
- Salakhutdinov, R. Learning Deep Generative Models. Ann. Rev. Stat. Appl. 2015, 2, 361–385. [Google Scholar] [CrossRef] [Green Version]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Zhang, N.; Ding, S.; Zhang, J.; Xue, Y. An Overview on Restricted Boltzmann Machines. Neurocomputing 2018, 275, 1186–1199. [Google Scholar] [CrossRef]
- Cui, Z.; Cao, Z.; Yang, J.; Ren, H. Hierarchical Recognition System for Target Recognition from Sparse Representations. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Liu, F.; Jiao, L.; Hou, B.; Yang, S. POL-SAR Image Classification Based on Wishart DBN and Local Spatial Information. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3292–3308. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Sun, W. Object-oriented Ensemble Classification for Polarimetric SAR Imagery Using Restricted Boltzmann Machines. Remote Sens. Lett. 2017, 8, 204–213. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, L.; Zhao, J.; Gu, J.; Zhao, J. Discriminant Deep Belief Network for High-Resolution SAR Image Classification. Pattern Recognit. 2017, 61, 686–701. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Implicit Mixtures of Restricted Boltzmann Machines. In Advances in Neural Information Processing Systems; Bengio, Y., Schuurmans, D., Lafferty, J., Williams, C., Culotta, A., Eds.; The MIT Press: Cambridge, MA, USA, 2009; pp. 1145–1152. [Google Scholar]
- Fischer, A.; Igel, C. Training Restricted Boltzmann Machines: An Introduction. Pattern Recognit. 2014, 47, 25–39. [Google Scholar] [CrossRef]
- Stacy, E.W. A Generalization of the Gamma Distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Li, H.C.; Hong, W.; Wu, Y.R.; Fan, P.Z. On the Empirical–Statistical Modeling of SAR Images With Generalized Gamma Distribution. IEEE J. Sel. Top. Signal Process. 2011, 5, 386–397. [Google Scholar] [CrossRef]
- Hinton, G.E. Training Products of Experts by Minimizing Contrastive Divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fischer, A.; Igel, C. Empirical Analysis of the Divergence of Gibbs Sampling Based Learning Algorithms for Restricted Boltzmann Machines. In Proceedings of the 20th International Conference on Artificial Neural Networks, Thessaloniki, Greece, 15–18 September 2010; Volume 6354, pp. 208–217. [Google Scholar]
- Upadhya, V.; Sastry, P.S. Learning RBM with a DC Programming Approach. In Proceedings of the Asian Conference on Machine Learning, Beijing, China, 15–17 November 2017; Volume 77, pp. 498–513. [Google Scholar]
- Carreira-Perpinán, M.A.; Hinton, G. On Contrastive Divergence Learning. In Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics (AISTATS), Bridgetown, Barbados, 6–8 January 2005; Volume 10, pp. 59–66. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hinton, G.E. Learning Multiple Layers of Representation. Trends Cognit. Sci. 2007, 11, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Salakhutdinov, R.; Hinton, G. An Efficient Learning Procedure for Deep Boltzmann Machines. Neural Comput. 2012, 24, 1967–2006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hinton, G.E.; Salakhutdinov, R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. Supervised High-Resolution Dual-Polarization SAR Image Classification by Finite Mixtures and Copulas. IEEE J. Sel. Top. Signal Process. 2011, 5, 554–566. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Wu, Y.; Zhang, P.; Zhang, Q.; Li, Y.; Li, M. SAR Target Configuration Recognition Using Locality Preserving Property and Gaussian Mixture Distribution. IEEE Geosci. Remote Sens. Lett. 2013, 10, 268–272. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Q.M.J.; Nguyen, T.M.; Sun, X. Synthetic Aperture Radar Image Segmentation by Modified Student’s t-Mixture Model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4391–4403. [Google Scholar] [CrossRef]
- Yang, W.; Dai, D.; Triggs, B.; Xia, G.S. SAR-Based Terrain Classification Using Weakly Supervised Hierarchical Markov Aspect Models. IEEE Trans. Image Process. 2012, 21, 4232–4243. [Google Scholar] [CrossRef] [PubMed]
- Kayabol, K.; Zerubia, J. Unsupervised Amplitude and Texture Classification of SAR Images With Multinomial Latent Model. IEEE Trans. Image Process. 2013, 22, 561–572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, C.; Zhuo, T.; Ou, D.; Liu, M.; Liao, M. Nonlinear Compressed Sensing-Based LDA Topic Model for Polarimetric SAR Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 972–982. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Cui, S.; Schwarz, G.; Datcu, M. A Comparative Study of Statistical Models for Multilook SAR Images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1752–1756. [Google Scholar] [CrossRef]
- Lobry, S.; Denis, L.; Tupin, F. Multitemporal SAR Image Decomposition into Strong Scatterers, Background, and Speckle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3419–3429. [Google Scholar] [CrossRef]
- Chierchia, G.; Gheche, M.E.; Scarpa, G.; Verdoliva, L. Multitemporal SAR Image Despeckling Based on Block-Matching and Collaborative Filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Varma, M.; Zisserman, A. A Statistical Approach to Material Classification Using Image Patch Exemplars. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2032–2047. [Google Scholar] [CrossRef] [PubMed]
- Dumitru, C.O.; Datcu, M. Information Content of Very High Resolution SAR Images: Study of Feature Extraction and Imaging Parameters. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4591–4610. [Google Scholar] [CrossRef] [Green Version]
- Roux, N.L.; Bengio, Y. Representational Power of Restricted Boltzmann Machines and Deep Belief Networks. Neural Comput. 2008, 20, 1631–1649. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Kamarainen, J.K.; Kyrki, V.; Kalviainen, H. Invariance Properties of Gabor Filter-Based Features-Overview and Applications. IEEE Trans. Image Process. 2006, 15, 1088–1099. [Google Scholar] [CrossRef] [PubMed]












| g-DBN | CNN-Based Approaches [19,20,21,24,52] | |
|---|---|---|
| Model | generative model | biological-inspired |
| Configuration | gB-RBM Binary-RBMs | convolutional layers pooling layers full-connection layers |
| Training | unsupervised training fine-tuning | dropout & dropconnect data augmentation pre-training & fine-tining low-rank & tensor decomposition |
| Dataset | ptSet1 | ptSet2 | ptSet3 | ptSet4 | ptSet5 | ptSet6 |
|---|---|---|---|---|---|---|
| Size of image patch | 21 × 21 | 25 × 25 | 29 × 29 | 33 × 33 | 37 × 37 | 41 × 41 |
| Num. of patches | 15,000 × 4 | |||||
| Dataset | ptSet1 | ptSet2 | ptSet3 | ptSet4 | ptSet5 | ptSet6 |
|---|---|---|---|---|---|---|
| Patch Vector | 48.30 ± 1.17 | 46.10 ± 1.50 | 44.78 ± 0.97 | 43.15 ± 1.15 | 42.97 ± 0.86 | 42.09 ± 1.31 |
| GLCM + Gabor | 64.62 ± 0.51 | 66.50 ± 0.47 | 68.44 ± 0.63 | 70.95 ± 0.37 | 72.45 ± 0.61 | 73.40 ± 0.41 |
| DBN | 60.72 ± 1.21 | 62.18 ± 0.44 | 66.43 ± 0.48 | 67.18 ± 0.58 | 67.41 ± 0.69 | 67.88 ± 1.60 |
| gΓ-DBN | 68.21 ± 3.18 | 69.75 ± 2.08 | 72.05 ± 0.86 | 73.14 ± 1.35 | 74.32 ± 0.94 | 75.56± 0.83 |
| Approaches | CPU Times | ptSet1 | ptSet2 | ptSet3 | ptSet4 | ptSet5 | ptSet6 |
|---|---|---|---|---|---|---|---|
| Patch Vector | ft. ext. | – | |||||
| SVM tr. | 1.12 × | 1.13 × | 1.15 × | 1.14 × | 1.14 × | 1.15 × | |
| GLCM + Gabor | ft. ext. | 661.41 | 653.92 | 671.01 | 661.35 | 679.68 | 671.69 |
| SVM tr. | 198.23 | 211.55 | 197.10 | 193.69 | 185.32 | 191.12 | |
| DBN | DBN tr. | 2.94 | 3.84 | 6.04 | 7.23 | 7.48 | 9.21 |
| DisNet | 1.81 | 2.36 | 3.82 | 3.89 | 5.26 | 6.35 | |
| gΓ-DBN | gΓ-DBN tr. | 7.63 | 9.90 | 12.79 | 15.56 | 19.68 | 34.73 |
| DisNet | 6.79 | 8.29 | 10.77 | 12.37 | 19.08 | 28.67 | |
| Patch Vector | GLCM + Gabor | DBN | g-DBN | |
|---|---|---|---|---|
| Patch partition | 3.85 | |||
| Feature Extraction | 0 | 1.31 × 10 | 0 | 0 |
| Classification | 1.14 × 10 | 307.31 | 6.79 | 7.94 |
| Hidden Layers | Num. of Units | Accuracy (100%) | CPU Times (s) | |
|---|---|---|---|---|
| Model Training | Testing | |||
| 1 | [1089, 100, 4] | 72.54 ± 1.15 | 20.01 ± 0.68 | 0.31 ± 0.01 |
| 2 | [1089, 400, 20, 4] | 73.22 ± 1.01 | 69.75 ± 3.78 | 0.92 ± 0.04 |
| 3 | [1089, 400, 100, 20, 4] | 72.71 ± 1.35 | 79.13 ± 3.35 | 1.17 ± 0.13 |
| 4 | [1089, 400, 200, 100, 20, 4] | 71.61 ± 1.43 | 87.83 ± 5.23 | 1.23 ± 0.29 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Guo, L.; Jia, M.; Wang, L. The Generalized Gamma-DBN for High-Resolution SAR Image Classification. Remote Sens. 2018, 10, 878. https://doi.org/10.3390/rs10060878
Zhao Z, Guo L, Jia M, Wang L. The Generalized Gamma-DBN for High-Resolution SAR Image Classification. Remote Sensing. 2018; 10(6):878. https://doi.org/10.3390/rs10060878
Chicago/Turabian StyleZhao, Zhiqiang, Lei Guo, Meng Jia, and Lei Wang. 2018. "The Generalized Gamma-DBN for High-Resolution SAR Image Classification" Remote Sensing 10, no. 6: 878. https://doi.org/10.3390/rs10060878
APA StyleZhao, Z., Guo, L., Jia, M., & Wang, L. (2018). The Generalized Gamma-DBN for High-Resolution SAR Image Classification. Remote Sensing, 10(6), 878. https://doi.org/10.3390/rs10060878