Figure 1.
Advanced Very High Resolution Radiometer (AVHRR) scenes subset available within the University of Bern data archive with the lakes covered by the present study. Blue dots are all lakes for which Lake Surface Water Temperature (LSWT) data was retrieved and analysed; the green dots are the location where validation with in-situ data was performed.
Figure 1.
Advanced Very High Resolution Radiometer (AVHRR) scenes subset available within the University of Bern data archive with the lakes covered by the present study. Blue dots are all lakes for which Lake Surface Water Temperature (LSWT) data was retrieved and analysed; the green dots are the location where validation with in-situ data was performed.
Figure 2.
Availability of AVHRR data by platform and by years. In blue, the data that was used for the present study, and, in red, the data that was not processed due to the elevated amount of inconsistent data.
Figure 2.
Availability of AVHRR data by platform and by years. In blue, the data that was used for the present study, and, in red, the data that was not processed due to the elevated amount of inconsistent data.
Figure 3.
Schematic representation of the LSWT processing as used for this work.
Figure 3.
Schematic representation of the LSWT processing as used for this work.
Figure 4.
Overpass times of all AVHRR scenes in which Lake Geneva is visible. Each dot represents a scene; the different colors represents different platforms.
Figure 4.
Overpass times of all AVHRR scenes in which Lake Geneva is visible. Each dot represents a scene; the different colors represents different platforms.
Figure 5.
Comparison for different season periods (JJA, JJAS, JAS) in the yearly temperature cycle at lake Constance, Müritz, and Lake Inari. The middle row, representing the seasonal periods as used during this study is well adapted to the actual annual cycles, as the summer temperature peak is in the center of the period.
Figure 5.
Comparison for different season periods (JJA, JJAS, JAS) in the yearly temperature cycle at lake Constance, Müritz, and Lake Inari. The middle row, representing the seasonal periods as used during this study is well adapted to the actual annual cycles, as the summer temperature peak is in the center of the period.
Figure 6.
The validation with hourly averaged measurements at Lake Constance for the station in Bregenz (a) and for the station in Lindau (b). Both show a good performance and a high number of matchups despite the in-situ locations close to the shore. However, the correlation with the satellite data is significantly higher in Bregenz (a) than in Lindau (b). For both validations, the same satellite data is used.
Figure 6.
The validation with hourly averaged measurements at Lake Constance for the station in Bregenz (a) and for the station in Lindau (b). Both show a good performance and a high number of matchups despite the in-situ locations close to the shore. However, the correlation with the satellite data is significantly higher in Bregenz (a) than in Lindau (b). For both validations, the same satellite data is used.
Figure 7.
The validation with sporadic instant measurement at Müritz (a) and at Lake Balaton (b). Both in-situ measurements where manually taken in open waters. The bi-monthly sampling frequency only allows for few matchups per year. Nevertheless, the measurements at Müritz yield the best performance thanks to close temporal matchups and the open waters. At Lake Balaton however, the exact timestamp was unknown (only day). Therefore, 12:00 local time was assumed, which led to less accurate temporal matchups and lower correlation.
Figure 7.
The validation with sporadic instant measurement at Müritz (a) and at Lake Balaton (b). Both in-situ measurements where manually taken in open waters. The bi-monthly sampling frequency only allows for few matchups per year. Nevertheless, the measurements at Müritz yield the best performance thanks to close temporal matchups and the open waters. At Lake Balaton however, the exact timestamp was unknown (only day). Therefore, 12:00 local time was assumed, which led to less accurate temporal matchups and lower correlation.
Figure 8.
The validation with daily in-situ measurement at Lake Geneva, INRA (a) and Inarijärvi (b). The validation at Lake Geneva INRA shows good performance and a high number of matchups through the whole year. At Inarijärvi, however, the weakest validation performance of all is found. Inarijärvi is located north of the polar cycle and has a long period of ice cover per year. Further, the in-situ measurement station is located within a very complex shore geometry with many small islands.
Figure 8.
The validation with daily in-situ measurement at Lake Geneva, INRA (a) and Inarijärvi (b). The validation at Lake Geneva INRA shows good performance and a high number of matchups through the whole year. At Inarijärvi, however, the weakest validation performance of all is found. Inarijärvi is located north of the polar cycle and has a long period of ice cover per year. Further, the in-situ measurement station is located within a very complex shore geometry with many small islands.
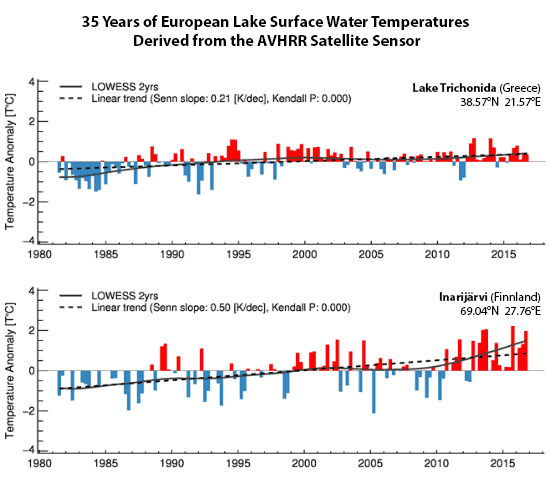
Figure 9.
Temperature trends of Lake Trichonidas (a), Inarijärvi (b), Thingvallavatn (c), and Lake Onega (d). Blue bars indicate temperatures below the long-term mean, whereas the red bars show warmer years. The dashed line shows the linear trend, whereas the solid black line shows the locally weighted scatterplot smoothing (LOWESS) over a 2-years period. Lake Trichonidas (a) is the lake with the lowest latitude (except for Djorf Torba), whereas Inarivjärvi (b) is the lake at highest latitude. The same applies for the longitude where it goes from Thingvallavatn (c) in the west to Lake Onega (d) in the east.
Figure 9.
Temperature trends of Lake Trichonidas (a), Inarijärvi (b), Thingvallavatn (c), and Lake Onega (d). Blue bars indicate temperatures below the long-term mean, whereas the red bars show warmer years. The dashed line shows the linear trend, whereas the solid black line shows the locally weighted scatterplot smoothing (LOWESS) over a 2-years period. Lake Trichonidas (a) is the lake with the lowest latitude (except for Djorf Torba), whereas Inarivjärvi (b) is the lake at highest latitude. The same applies for the longitude where it goes from Thingvallavatn (c) in the west to Lake Onega (d) in the east.
Figure 10.
South–north gradient (a) and the west–east gradient (b) of the yearly LSWT trend. The red dashed line is a simple linear model derived with least square regression, and R2 is the coefficient of determination.
Figure 10.
South–north gradient (a) and the west–east gradient (b) of the yearly LSWT trend. The red dashed line is a simple linear model derived with least square regression, and R2 is the coefficient of determination.
Figure 11.
South–North gradient of seasonal trends from European lakes. The dashed lines are simple linear models derived with least square regression of the data points. The reservoirs lakes are excluded from the graph.
Figure 11.
South–North gradient of seasonal trends from European lakes. The dashed lines are simple linear models derived with least square regression of the data points. The reservoirs lakes are excluded from the graph.
Figure 12.
Seasonal trends at Lake Sanguinet, whereas the spring and summer trend are categorized as ‘significant’ (p-value < 0.05); the winter and autumn trends 0.11 K/decade are categorized ‘insignificant’ (p-values > 0.05).
Figure 12.
Seasonal trends at Lake Sanguinet, whereas the spring and summer trend are categorized as ‘significant’ (p-value < 0.05); the winter and autumn trends 0.11 K/decade are categorized ‘insignificant’ (p-values > 0.05).
Figure 13.
Comparison of LSWT trends with local air temperature trends (extracted from ERA INTERIM) at Lake Vättern (a), Lake Constance (b), and Lake Bolsena (c).
Figure 13.
Comparison of LSWT trends with local air temperature trends (extracted from ERA INTERIM) at Lake Vättern (a), Lake Constance (b), and Lake Bolsena (c).
Figure 14.
Comparison of the Yearly Temperature Cycle from two different 15-years-periods at Lake Bolsena (a), Lake Constance (b), Lake Vättern (c), and Lake Onega (d). The red and the blue lines represent the yearly cycle of the two periods; the black line is the difference between the two periods.
Figure 14.
Comparison of the Yearly Temperature Cycle from two different 15-years-periods at Lake Bolsena (a), Lake Constance (b), Lake Vättern (c), and Lake Onega (d). The red and the blue lines represent the yearly cycle of the two periods; the black line is the difference between the two periods.
Figure 15.
Significant difference in trends within Lake Peipus when comparing the trend near the Mehikoorma in-situ station (see coordinates in
Table 2) with the trend in the open waters of the northern part (see coordinates in
Table 1).
Figure 15.
Significant difference in trends within Lake Peipus when comparing the trend near the Mehikoorma in-situ station (see coordinates in
Table 2) with the trend in the open waters of the northern part (see coordinates in
Table 1).
Table 1.
List of Lakes where LSWT was retrieved and trend analysis performed. The acronyms are the same as those used in
Figure 1.
Table 1.
List of Lakes where LSWT was retrieved and trend analysis performed. The acronyms are the same as those used in
Figure 1.
| Lake Name | Country | Acr. | Location | Alt. [m] | Area [km2] | Depth Ø [m] | In-Situ Data |
|---|
| Lake Balaton | HU | Bala | 46.75°N | 17.43°E | 126 | 578 | 3.3 | Yes |
| Lake Bolsena | IT | Bols | 42.61°N | 11.93°E | 368 | 114 | 81.0 | No |
| Lake Constance | DE,CH,AUT | Cons | 47.60°N | 9.45°E | 431 | 472 | 101.0 | Yes |
| Djorf Torba | DZA | Djor | 31.53°N | 2.75°W | 716 | 77 | 6.1 | No |
| Lake Garda | IT | Gard | 45.52°N | 10.67°E | 85 | 368 | 133.0 | No |
| Lake Geneva | FR, CH | Gene | 46.41°N | 6.41°E | 466 | 580 | 152.7 | Yes |
| Inarijärvi | FIN | Inar | 69.04°N | 27.76°E | 126 | 1′110 | 14.0 | Yes |
| Kiev Reservoir | UA | Kiye | 50.80°N | 30.47°E | 93 | 420 | 4.0 | No |
| Lappajärvi | FIN | Lapp | 63.13°N | 23.71°E | 85 | 141 | 7.0 | Yes |
| Lokka Reservoir | FIN | Loka | 67.94°N | 27.56°E | 259 | 488 | 5.0 | No |
| Müritz | DE | Muri | 53.43°N | 12.67°E | 63 | 110 | 6.5 | Yes |
| Lough Neagh | NIR | Neag | 54.62°N | 6.41°W | 58 | 380 | 9.0 | No |
| Lake Ohrid | MK,ALB | Ohri | 41.02°N | 20.72°E | 700 | 347 | 155.0 | No |
| Lake Onega | RU | Oneg | 61.63°N | 35.53°E | 56 | 9′608 | 30.0 | No |
| Oulujärvi | FIN | Oulu | 64.29°N | 27.22°E | 128 | 890 | 7.6 | Yes |
| Lake Päijiänne | FIN | Paij | 61.52°N | 25.42°E | 95 | 1′080 | 16.0 | Yes |
| Lake Peipus | EST,RU | Peip | 58.53°N | 27.50°E | 29 | 3′553 | 7.1 | Yes |
| Lake Pielinen | FIN | Piel | 63.24°N | 29.64°E | 113 | 870 | 9.0 | Yes |
| Säkylän Pyhäjärvi | FIN | Pyhj | 61.00°N | 22.28°E | 52 | 150 | 5.5 | Yes |
| Pyhäselkä | FIN | Oriv | 62.60°N | 29.77°E | 76 | 361 | 8.7 | Yes |
| Sanguinet | FR | Sang | 44.49°N | 1.15°W | 24 | 57 | 5.0 | No |
| Thingvallavatn | IS | Thin | 64.16°N | 21.13°W | 105 | 83 | 34.0 | No |
| Lake Trichonida | GR | Tric | 38.57°N | 21.57°E | 40 | 95 | 30.0 | Yes |
| Lake Vänern | SWE | Vane | 59.07°N | 13.60°E | 45 | 5′650 | 27.0 | No |
| Lake Vättern | SWE | Vatt | 58.33°N | 14.50°E | 91 | 1′890 | 40.0 | No |
| Lake Yalpuh | UA | Yalp | 45.42°N | 28.63°E | 10 | 225 | 2.0 | No |
Table 2.
List of in-situ measuring locations from which data was available for this study. Most of the measurements are either hourly or daily averaged temperatures from automatic stations. In the case of Müritz, Lake Trichonida, and the older measurements from Lake Balaton, the measurements are sporadically and manually taken at specific locations on the lake. The average measurement density varies from 12 measurements per year at Lake Trichonida (monthly measurements) to 8760 measurements per year at Bregenz, Lake Constance (hourly measurements).
Table 2.
List of in-situ measuring locations from which data was available for this study. Most of the measurements are either hourly or daily averaged temperatures from automatic stations. In the case of Müritz, Lake Trichonida, and the older measurements from Lake Balaton, the measurements are sporadically and manually taken at specific locations on the lake. The average measurement density varies from 12 measurements per year at Lake Trichonida (monthly measurements) to 8760 measurements per year at Bregenz, Lake Constance (hourly measurements).
| Lake | Country | Sta. Name | Type/Freq. | Coverage | N/Yr | Location |
|---|
| Lake Balaton | HU | Keszthely old | instant | 1981–2003 | 21 | 46.74°N 17.29°E |
| Keszthely | hourly | 2003–2013 | 4′043 | 46.76°N 17.27°E |
| Siofok | daily | 1992–2012 | 365 | 46.90°N 18.05°E |
| Lake Constance | DE, CH AUT | Bregenz old | daily | 1989–1996 | 365 | 47.51°N 9.74°E |
| Bregenz new | hourly | 1997–2009 | 8′760 | 47.51°N 9.74°E |
| Lindau | hourly | 2005–2014 | 8′261 | 47.54°N 9.68°E |
| Lake Geneva | FR, CH | Buchillon | hourly | 2000–2011 | 8′147 | 46.46°N 6.40°E |
| INRA | daily | 1991–2011 | 360 | 46.38°N 6.47°E |
| Lake Inari | FIN | Inari | daily | 1980–2014 | 153 | 68.90°N 28.10°E |
| Lappajärvi | FIN | Halkosaari | daily | 1980–2014 | 167 | 63.26°N 23.63°E |
| Müritz | DE | Müritz | instant | 1980–2013 | 18 | 53.42°N 12.70°E |
| Pyhäjärvi | FIN | Säkylän | daily | 1996–2014 | 205 | 61.11°N 22.17°E |
| Oulujärvi | FIN | Oulujärvi | daily | 1980–2014 | 156 | 64.40°N 27.17°E |
| Lake Paijiänne | FIN | Päijätsalo | daily | 2003–2014 | 200 | 61.47°N 25.59°E |
| Kalkkinen | daily | 1980–1999 | 214 | 61.29°N 25.57°E |
| Lake Peipsi | EST, RU | Mehikoorma | daily | 1985–2011 | 267 | 58.24°N |
| Lake Pielinen | FIN | Nurmes | daily | 1980–2014 | 163 | 63.54°N |
| Pyhäselkä | FIN | Joensuu | daily | 1980–2014 | 194 | 62.60°N |
| Lake Trichonida | GRE | Trichonida | instant | 2004–2006 | 12 | 38.57°N |
Table 3.
The six quality levels indicate which additional tests are passed. The levels are cumulative (e.g., Q4 means Q3 AND VZA < 55). The average data availability (compared to Q1) and the average standard deviation during the validation are shown for the different quality levels.
Table 3.
The six quality levels indicate which additional tests are passed. The levels are cumulative (e.g., Q4 means Q3 AND VZA < 55). The average data availability (compared to Q1) and the average standard deviation during the validation are shown for the different quality levels.
| Quality Level | Perc. N (%) | Stddev |
|---|
| Q1 | valid pixels * | 100.0% | 1.399 |
| Q2 | SSDEV < 3 | 99.9% | 1.395 |
| Q3 | no Sun glint | 95.9% | 1.390 |
| Q4 | VZA < 55 | 89.7% | 1.362 |
| Q5 | VZA < 45 | 83.7% | 1.344 |
| Q6 | feature detection passed ** | 66.4% | 1.333 |
Table 4.
Validation results for each in-situ station. The data is ordered by latitude from south to north. The measurement type describes the averaging of the in-situ measurement: daily averaged, hourly averaged, and instant measurements. Instant measurements are single measurements that were manually taken during measurement campaigns. As the exact timestamps for the instant measurements where not known at Lake Balaton (Kesztehly old) and Lake Trichonida, 12:00 local time is assumed.
Table 4.
Validation results for each in-situ station. The data is ordered by latitude from south to north. The measurement type describes the averaging of the in-situ measurement: daily averaged, hourly averaged, and instant measurements. Instant measurements are single measurements that were manually taken during measurement campaigns. As the exact timestamps for the instant measurements where not known at Lake Balaton (Kesztehly old) and Lake Trichonida, 12:00 local time is assumed.
| Location | Type | Location | n Match | R | RMSE | BIAS ± SD |
|---|
| Lake Trichonida | Instant * | 38.57°N | 21.56°E | 16 | 0.987 | 1.59 | −1.23 ± 1.04 |
| Geneva INRA | daily | 46.38°N | 6.47°E | 2453 | 0.985 | 1.08 | 0.26 ± 1.05 |
| Geneva Buchillon | hourly | 46.46°N | 6.40°E | 2373 | 0.981 | 1.29 | −0.52 ± 1.18 |
| Balaton Kesztehly old | Instant * | 46.74°N | 17.29°E | 114 | 0.982 | 1.54 | −0.57 ± 1.44 |
| Balaton Keszthely new | hourly | 46.76°N | 17.27°E | 1050 | 0.966 | 1.45 | 0.69 ± 1.27 |
| Balaton Siofok | daily | 46.90°N | 18.05°E | 2834 | 0.985 | 1.47 | −0.54 ± 1.36 |
| Constance Bregenz new | hourly | 47.51°N | 9.74°E | 1723 | 0.990 | 1.01 | 0.36 ± 0.95 |
| Constance Bregenz old | daily | 47.51°N | 9.74°E | 719 | 0.981 | 1.37 | 0.50 ± 1.28 |
| Constance Lindau | hourly | 47.54°N | 9.68°E | 1755 | 0.976 | 1.53 | 0.63 ± 1.40 |
| Müritz | instant | 53.42°N | 12.70°E | 66 | 0.989 | 0.82 | −0.07 ± 0.82 |
| Peipsi Mehikoorma | daily | 58.24°N | 27.48°E | 2102 | 0.984 | 1.25 | 0.44 ± 1.17 |
| Pyhäjärvi Säkylä | daily | 61.11°N | 22.17°E | 1749 | 0.975 | 1.26 | 0.36 ± 1.21 |
| Päijänne Päjätsalo | daily | 61.29°N | 25.57°E | 1017 | 0.947 | 2.06 | 1.28 ± 1.61 |
| Päijänne Kalkkinen | daily | 61.47°N | 25.59°E | 722 | 0.964 | 1.49 | −0.61 ± 1.36 |
| Pyhäselka Joensuu | daily | 62.60°N | 29.77°E | 1893 | 0.962 | 1.46 | 0.11 ± 1.46 |
| Lappajärvi | daily | 63.26°N | 23.63°E | 2044 | 0.949 | 1.57 | 0.25 ± 1.55 |
| Pielinen | daily | 63.54°N | 29.13°E | 1707 | 0.938 | 1.83 | 0.45 ± 1.77 |
| Oulujärvi | daily | 64.40°N | 27.17°E | 1973 | 0.926 | 1.93 | 0.56 ± 1.84 |
| Inarijärvi | daily | 68.90°N | 28.10°E | 1207 | 0.896 | 2.60 | 1.65 ± 2.01 |
Table 5.
Impact of the DTC correction on the validation with daily in-situ data. Whereas for Lake Balaton Siofok, the improvement is neglectable, a considerable performance improvement is observed, for example, at Lake Constance, Bregenz old.
Table 5.
Impact of the DTC correction on the validation with daily in-situ data. Whereas for Lake Balaton Siofok, the improvement is neglectable, a considerable performance improvement is observed, for example, at Lake Constance, Bregenz old.
| Location | BIAS ± SD | SD Change |
|---|
| Raw LSWT | DTC Corr. |
|---|
| Balaton Siofok | −1.05 ± 1.37 | −0.54 ± 1.36 | −0.1% |
| Päijänne Päjätsalo | 1.11 ± 1.63 | 1.28 ± 1.61 | −1.4% |
| Peipsi Mehikoorma | 0.01 ± 1.22 | 0.44 ± 1.17 | −3.5% |
| Pyhäjärvi Säkylä | 0.12 ± 1.26 | 0.36 ± 1.21 | −4.2% |
| Pyhäselka Joensuu | −0.07 ± 1.52 | 0.11 ± 1.46 | −4.3% |
| Päijänne Kalkkinen | −0.75 ± 1.42 | −0.61 ± 1.36 | −4.7% |
| Pielinen | 0.31 ± 1.87 | 0.45 ± 1.77 | −5.1% |
| Geneva INRA | −0.09 ± 1.11 | 0.26 ± 1.05 | −5.5% |
| Lappajärvi | 0.13 ± 1.67 | 0.25 ± 1.55 | −7.5% |
| Oulujärvi | 0.52 ± 2.00 | 0.56 ± 1.84 | −7.9% |
| Inarijärvi | 1.59 ± 2.37 | 1.65 ± 2.01 | −15.5% |
| Constance, Bregenz old | −0.01 ± 1.51 | 0.50 ± 1.28 | −15.6% |
Table 6.
Comparison of trends from satellite-derived LSWT with trends from in-situ data records. Only in-situ stations with data covering at least 25 years were used. The difference between DTC-adjusted trends and in-situ trends, as well as the difference between raw LSWT trends and in-situ trends, is shown in the last two columns.
Table 6.
Comparison of trends from satellite-derived LSWT with trends from in-situ data records. Only in-situ stations with data covering at least 25 years were used. The difference between DTC-adjusted trends and in-situ trends, as well as the difference between raw LSWT trends and in-situ trends, is shown in the last two columns.
| Locations | Yr | In-Situ Trend | DTC Trend | RAW Trend | Diff. with In-Situ |
|---|
| senn | p | senn | p | senn | p | DTC | RAW |
|---|
| Inarijärvi | 31 | 0.42 | 0.000 | 0.45 | 0.000 | 0.58 | 0.000 | 0.03 | 0.16 |
| Pyhäselka Joensuu | 32 | 0.58 | 0.000 | 0.59 | 0.000 | 0.56 | 0.000 | 0.00 | 0.02 |
| Peipsi Mehikoorma | 26 | 0.44 | 0.000 | 0.44 | 0.003 | 0.45 | 0.004 | 0.00 | 0.01 |
| Lappajärvi | 31 | 0.45 | 0.000 | 0.50 | 0.000 | 0.22 | 1.000 | 0.05 | 0.23 |
| Pielinen | 31 | 0.50 | 0.000 | 0.64 | 0.000 | 0.53 | 0.000 | 0.14 | 0.03 |
| Oulujärvi | 31 | 0.43 | 0.000 | 0.49 | 0.000 | 0.59 | 0.000 | 0.06 | 0.15 |
| | | | | | | | | 0.05 | 0.10 |
Table 7.
Yearly and seasonal trends at all studied locations ordered from South to North. The covered period is slightly below the maximum of 36 years, depending on availability of cloud-free scenes at each location. The grayed-out values are trends (K/dec) in which Kendall p-value > 0.They are not retained to compute the average trends showed on the last line. The strongest seasonal trend of each lake is marked with an asterisk. Blank values signify that there were not enough values to compute trends, mostly due to ice cover during the cold period.
Table 7.
Yearly and seasonal trends at all studied locations ordered from South to North. The covered period is slightly below the maximum of 36 years, depending on availability of cloud-free scenes at each location. The grayed-out values are trends (K/dec) in which Kendall p-value > 0.They are not retained to compute the average trends showed on the last line. The strongest seasonal trend of each lake is marked with an asterisk. Blank values signify that there were not enough values to compute trends, mostly due to ice cover during the cold period.
| Location | Period | Yearly | Winter | Spring | Summer | Autumn |
|---|
| Yrs | senn | p | senn | p | senn | p | senn | p | senn | p |
|---|
| Djorf Torba | 34.9 | 0.17 | 0.03 | −0.08 | 0.72 | 0.07 | 0.67 | 0.47 * | 0.00 | 0.20 | 0.23 |
| Lake Trichonida | 35.5 | 0.21 | 0.00 | 0.40 * | 0.00 | 0.18 | 0.02 | 0.18 | 0.00 | 0.16 | 0.16 |
| Lake Ohrid | 35.5 | 0.29 | 0.00 | 0.44 * | 0.00 | 0.18 | 0.10 | 0.32 | 0.00 | 0.23 | 0.03 |
| Lake Bolsena | 35.5 | 0.28 | 0.00 | 0.46 * | 0.00 | 0.37 | 0.00 | 0.25 | 0.02 | 0.09 | 0.25 |
| Sanguinet | 35.4 | 0.21 | 0.00 | 0.11 | 0.43 | 0.41 * | 0.00 | 0.22 | 0.03 | 0.11 | 0.37 |
| Lake Yalpuh | 35.4 | 0.36 | 0.00 | 0.15 | 0.55 | 0.43 | 0.05 | 0.63 * | 0.00 | 0.23 | 0.09 |
| Lake Garda | 35.4 | 0.37 | 0.00 | 0.53 * | 0.00 | 0.37 | 0.00 | 0.29 | 0.00 | 0.30 | 0.01 |
| Lake Geneva | 35.5 | 0.33 | 0.00 | 0.44 * | 0.00 | 0.38 | 0.01 | 0.26 | 0.02 | 0.29 | 0.03 |
| Lake Balaton | 35.4 | 0.34 | 0.00 | 0.17 | 0.57 | 0.54 * | 0.00 | 0.53 | 0.00 | 0.12 | 0.29 |
| Lake Constance | 35.5 | 0.39 | 0.00 | 0.50 * | 0.00 | 0.36 | 0.00 | 0.32 | 0.00 | 0.35 | 0.00 |
| Kiev Reservoir | 35.4 | 0.30 | 0.00 | 0.01 | 0.66 | 0.24 | 0.21 | 0.45 | 0.00 | 0.46 * | 0.03 |
| Müritz | 35.4 | 0.39 | 0.00 | 0.10 | 0.55 | 0.69 * | 0.00 | 0.30 | 0.04 | 0.38 | 0.02 |
| Lough Neagh | 35.4 | 0.33 | 0.00 | 0.40 | 0.02 | 0.45 | 0.00 | 0.04 | 0.83 | 0.46 * | 0.00 |
| Vättern | 35.5 | 0.49 | 0.00 | 0.46 | 0.00 | 0.57 * | 0.00 | 0.32 | 0.01 | 0.56 | 0.00 |
| Lake Peipus | 35.3 | 0.24 | 0.01 | 0.54 | 0.10 | 0.13 | 0.53 | 0.25 | 0.08 | 0.32 * | 0.05 |
| Vänern | 35.4 | 0.42 | 0.00 | 0.35 | 0.03 | 0.36 | 0.04 | 0.31 | 0.02 | 0.54 * | 0.00 |
| Pyhäjärvi | 35.3 | 0.54 | 0.00 | 0.57 | 0.05 | 0.47 | 0.05 | 0.57 * | 0.00 | 0.54 | 0.00 |
| Lake Päijiänne | 35.4 | 0.47 | 0.00 | 0.76 | 0.18 | 0.45 | 0.04 | 0.50 * | 0.00 | 0.49 | 0.00 |
| Lake Onega | 35.2 | 0.76 | 0.00 | | | 0.84 | 0.00 | 0.85 * | 0.00 | 0.63 | 0.00 |
| Pyhäselkä | 35.3 | 0.55 | 0.00 | | | 0.54 | 0.01 | 0.53 | 0.01 | 0.57 * | 0.00 |
| Lappajärvi | 35.2 | 0.45 | 0.00 | | | 0.40 | 0.16 | 0.45 | 0.01 | 0.57 * | 0.00 |
| Pielinen | 35.3 | 0.48 | 0.00 | | | 0.39 | 0.26 | 0.44 | 0.01 | 0.61 * | 0.00 |
| Thingvallavatn | 35.3 | 0.38 | 0.00 | | | 0.49 * | 0.00 | 0.35 | 0.01 | 0.49 * | 0.00 |
| Oulujärvi | 35.3 | 0.53 | 0.00 | | | 0.52 | 0.03 | 0.45 | 0.00 | 0.68 * | 0.00 |
| Lokka Reservoir | 35.3 | 0.51 | 0.00 | | | | | 0.52 | 0.00 | 0.89 * | 0.00 |
| Inarijärvi | 35.3 | 0.50 | 0.00 | | | | | 0.46 | 0.01 | 0.82 * | 0.00 |
| AVG (p < 0.05) | | 0.40 | | 0.44 | | 0.47 | | 0.41 | | 0.51 | |