Mapping Mangrove Forests Based on Multi-Tidal High-Resolution Satellite Imagery
Abstract
:1. Introduction
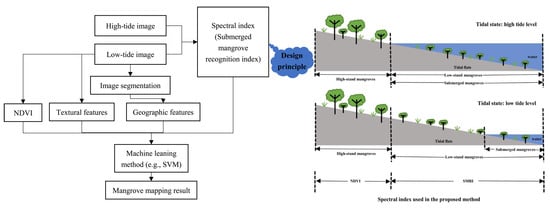
2. Basic Idea
3. Materials and the Detailed Method
3.1. Study Area and Data Preparation
3.2. Extraction of Spectral Indices
3.3. Textural Feature Extraction
3.4. Object-Based Classification with an SVM
4. Evaluation Method
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giri, C.; Long, J.; Tieszen, L. Mapping and Monitoring Louisiana’s Mangroves in the Aftermath of the 2010 Gulf of Mexico Oil Spill. J. Coast. Res. 2011, 277, 1059–1064. [Google Scholar] [CrossRef]
- Zhang, X.; Treitz, P.; Chen, D.; Quan, C.; Shi, L.; Li, X. Mapping mangrove forests using multi-tidal remotely-sensed data and a decision-tree based procedure. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 201–214. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Zhang, Y.; Ren, C.; Song, K. Landsat-based estimation of mangrove forest loss and restoration in Guangxi province, China, influenced by human and natural factors. IEEE J. Sel. Top. Appl. Earth Obs. 2015, 8, 311–323. [Google Scholar] [CrossRef]
- Vo, Q.; Oppelt, N.; Leinenkugel, P.; Kuenzer, C. Remote sensing in mapping mangrove ecosystems—An object-based approach. Remote Sens. 2013, 5, 183–201. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef] [Green Version]
- Walters, B.; Ronnback, P.; Kovacs, J.; Crona, B.; Hussain, S.; Badola, R.; Primavera, J.; Barbier, E.; Dahdouh-Guebas, F. Ethnobiology, socio-economics and management of mangrove forests: A review. Aquat. Bot. 2008, 89, 220–236. [Google Scholar] [CrossRef] [Green Version]
- Abd-El Monsef, H.; Smith, S. A new approach for estimating mangrove canopy cover using Landsat 8 imagery. Comput. Electron. Agric. 2017, 135, 183–194. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Li, L.; Song, K.; Ren, C.; Liu, B.; Mao, D. Mapping China’s mangroves based on an object-oriented classification of Landsat imagery. Wetlands 2014, 34, 277–283. [Google Scholar] [CrossRef]
- Giri, C.; Zhu, Z.; Tieszen, L.; Singh, A.; Gillette, S.; Kelmelis, J. Mangrove forest distributions and dynamics (1975–2005) of the tsunami-affected region of Asia. J. Biogeogr. 2008, 35, 519–528. [Google Scholar] [CrossRef] [Green Version]
- Lovelock, C.; Cahoon, D.; Friess, D.; Guntenspergen, G.; Krauss, K.; Reef, R.; Rogers, K.; Saunders, M.; Sidik, F.; Swales, A.; et al. The vulnerability of Indo-Pacific mangrove forests to sea-level rise. Nature 2015, 526, 559–563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirui, K.; Kairo, J.; Bosire, J.; Viergever, K.; Rudra, S.; Huxham, M.; Briers, R. Mapping of mangrove forest land cover change along the Kenya coastline using Landsat imagery. Ocean Coast. Manag. 2013, 83, 19–24. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Giri, C. Mapping the Philippines’ mangrove forests using Landsat imagery. Sensors 2011, 11, 2972–2981. [Google Scholar] [CrossRef] [PubMed]
- Everitt, J.; Yang, C.; Sriharan, S.; Judd, F. Using High Resolution Satellite Imagery to Map Black Mangrove on the Texas Gulf Coast. J. Coast. Res. 2008, 246, 1582–1586. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Lin, H.; Fang, C. Textural–Spectral Feature-Based Species Classification of Mangroves in Mai Po Nature Reserve from Worldview-3 Imagery. Remote Sens. 2016, 8, 24. [Google Scholar] [CrossRef]
- Xun, L.; Wang, L. An object-based SVM method incorporating optimal segmentation scale estimation using Bhattacharyya Distance for mapping salt cedar (Tamarisk spp.) with QuickBird imagery. GISci. Remote Sens. 2015, 52, 257–273. [Google Scholar] [CrossRef]
- Heenkenda, M.; Joyce, K.; Maier, S.; Bartolo, R. Mangrove species identification: Comparing WorldView-2 with aerial photographs. Remote Sens. 2014, 6, 6064–6088. [Google Scholar] [CrossRef]
- Kux, H.; Souza, U. Object-based image analysis of WORLDVIEW-2 satellite data for the classification of mangrove areas in the city of São Luís, Maranhão State, Brazil. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 4, 95–100. [Google Scholar] [CrossRef]
- Malinverni, E.; Tassetti, A.; Mancini, A.; Zingaretti, P.; Frontoni, E.; Bernardini, A. Hybrid object-based approach for land use/land cover mapping using high spatial resolution imagery. Int. J. Geogr. Inf. Sci. 2011, 25, 1025–1043. [Google Scholar] [CrossRef]
- Manson, F.; Loneragan, N.; Mcleod, I.; Kenyon, R. Assessing techniques for estimating the extent of mangroves: Topographic maps, aerial photographs and Landsat TM images. Mar. Freshw. Res. 2001, 52, 787–792. [Google Scholar] [CrossRef]
- Heumann, B. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Mitra, D.; Karmaker, S. Mangrove Classification in Sundarban using High Resolution Multi-Spectral Remote Sensing Data and GIS. Asian J. Environ. Disaster Manag. 2010, 2, 197. [Google Scholar] [CrossRef]
- Neukermans, G.; Dahdouh-Guebas, F.; Kairo, J.; Koedam, N. Mangrove species and stand mapping in Gazi Bay (Kenya) using Quickbird satellite imagery. J. Spat. Sci. 2008, 53, 75–86. [Google Scholar] [CrossRef]
- Green, E.; Clark, C.; Mumby, P.; Edwards, A.; Ellis, A. Remote sensing techniques for mangrove mapping. Int. J. Remote Sens. 1998, 19, 935–956. [Google Scholar] [CrossRef] [Green Version]
- Giri, C.; Pengra, P.; Zhu, Z.; Singh, A.; Tieszen, L. Monitoring mangrove forest dynamics of the Sundarbans in Bangladesh and India using multi-temporal satellite data from 1973 to 2000. Est. Coast. Shelf Sci. 2007, 73, 91–100. [Google Scholar] [CrossRef]
- Everitt, J.; Judd, F.; Escobar, D.; Davis, M. Integration of remote sensing and spatial information technologies for mapping black mangrove on the Texas gulf coast. J. Coast. Res. 1996, 12, 64–69. [Google Scholar]
- Li, M.; Lee, S. Mangroves of China: A brief review. For. Ecol. Manag. 1997, 96, 241–259. [Google Scholar] [CrossRef]
- Alongi, D. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Hernández Cornejo, R.; Koedam, N.; Ruiz Luna, A.; Troell, M.; Dahdouh-Guebas, F. Remote sensing and ethnobotanical assessment of the mangrove forest changes in the Navachiste-San Ignacio-Macapule lagoon complex, Sinaloa, Mexico. Ecol. Soc. 2005, 10, 16. [Google Scholar] [CrossRef]
- Helmer, E.; Kennaway, T.; Pedreros, D. Land cover and forest formation distributions for St. Kitts, Nevis, St. Eustatius, Grenada and Barbados from decision tree classification of cloud-cleared satellite imagery. Caribb. J. Sci. 2008, 44, 175–198. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P. Support vector machines for classification in remote sensing. Int. J. Remote Sens. 2005, 26, 1007–1011. [Google Scholar] [CrossRef]
- Yu, X.; Shao, H.; Liu, X.; Zhao, D. Applying Neural Network Classification to Obtain Mangrove Landscape Characteristics for Monitoring the Travel Environment Quality on the Beihai Coast of Guangxi, PR China. CLEAN–Soil Air Water 2010, 38, 289–295. [Google Scholar] [CrossRef]
- Wang, L.; Silván-Cárdenas, J.; Sousa, W. Neural network classification of mangrove species from multi-seasonal Ikonos imagery. Photogram. Eng. Rem. Sens. 2008, 74, 921–927. [Google Scholar] [CrossRef]
- Gao, J.; Chen, H.; Zhang, Y.; Zha, Y. Knowledge-based approaches to accurate mapping of mangroves from satellite data. Photogram. Eng. Remote Sens. 2004, 70, 1241–1248. [Google Scholar] [CrossRef]
- Foody, G.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Xin, H.; Zhang, L.; Wang, L. Evaluation of Morphological Texture Features for Mangrove Forest Mapping and Species Discrimination Using Multispectral IKONOS Imagery. IEEE Geosci. Remote Sens. 2009, 6, 393–397. [Google Scholar] [Green Version]
- Li, H.; Fu, H.; Han, Y.; Yang, J. Object-oriented classification of high-resolution remote sensing imagery based on an improved colour structure code and a support vector machine. Int. J. Remote Sens. 2010, 31, 1453–1470. [Google Scholar] [CrossRef]
- Harken, J.; Sugumaran, R. Classification of Iowa Wetlands Using an Airborne Hyperspectral Image: A Comparison of the Spectral Angle Mapper Classifier and an Object- Oriented Approach. Can. J. Remote Sens. 2005, 31, 167–174. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P. Mapping Salt-Marsh Land-Cover Vegetation Using High-Spatial and Hyperspectral Satellite Data to Assist Wetland Inventory. GISci. Remote Sens. 2014, 51, 483–497. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S. Hyperspectral data for mangrove species mapping: A comparison of pixel-based and object-based approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef]
- Kanniah, K.; Wai, N.; Shin, A.; Rasib, A. Per-pixel and sub-pixel classifications of high-resolution satellite data for mangrove species mapping. Appl. GIS 2007, 3, 1–22. [Google Scholar]
- Wang, L.; Sousa, W.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Genelett, D.; Gorte, B. A method for object-oriented land cover classification combining Landsat TM data and aerial photographs. Int. J. Remote Sens. 2003, 24, 1273–1286. [Google Scholar] [CrossRef]
- Conchedda, G.; Durieux, L.; Mayaux, P. An object-based method for mapping and change analysis in mangrove ecosystems. ISPRS J. Photogram. Remote Sens. 2008, 63, 578–589. [Google Scholar] [CrossRef]
- Flores De Santiago, F.; Kovacs, J.; Lafrance, P. An object-oriented classification method for mapping mangroves in Guinea, West Africa, using multipolarized ALOS PALSAR L-band data. Int. J. Remote Sens. 2013, 34, 563–586. [Google Scholar] [CrossRef]
- Li, M.; Mao, L.; Shen, W.; Liu, S.; Wei, A. Change and fragmentation trends of Zhanjiang mangrove forests in southern China using multi-temporal Landsat imagery (1977–2010). Estuar. Coast. Shelf Sci. 2013, 130, 111–120. [Google Scholar] [CrossRef]
- Rogers, K.; Lymburner, L.; Salum, R.; Brooke, B.; Woodroffe, C. Mapping of mangrove extent and zonation using high and low tide composites of Landsat data. Hydrobiologia 2017, 803, 49–68. [Google Scholar] [CrossRef]
- Collins, D.; Avdis, A.; Allison, P.; Johnson, H.; Hill, J.; Piggott, M.; Hassan, M.; Damit, A. Tidal dynamics and mangrove carbon sequestration during the Oligo–Miocene in the South China Sea. Nat. Commun. 2017, 8, 15698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.; Tian, Q.; Yu, T.; Gu, X. The extraction of mangrove within intertidal zone based on multi-temporal HJ CCD images. In Proceedings of the 17th China Conference on Remote Sensing, Beijing, China, 27–31 August 2010. [Google Scholar]
- Satyanarayana, B.; Mohamad, K.; Idris, I.; Husain, M.; Dahdouh-Guebas, F. Assessment of mangrove vegetation based on remote sensing and ground-truth measurements at Tumpat, Kelantan Delta, East Coast of Peninsular Malaysia. Int. J. Remote Sens. 2011, 32, 1635–1650. [Google Scholar] [CrossRef]
- Nardin, W.; Locatelli, S.; Pasquarella, V.; Rulli, M.; Woodcock, C.; Fagherazzi, S. Dynamics of a fringe mangrove forest detected by Landsat images in the Mekong River Delta, Vietnam. Earth Surf. Proc. Landf. 2016, 41, 2024–2037. [Google Scholar] [CrossRef]
- Giri, S.; Mukhopadhyay, A.; Hazra, S.; Mukherjee, S.; Roy, D.; Ghosh, S.; Ghosh, T.; Mitra, D. A study on abundance and distribution of mangrove species in Indian Sundarban using remote sensing technique. J. Coast. Conserv. 2014, 18, 359–367. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Zhang, L. A multichannel gray level co-occurrence matrix for multi/hyperspectral image texture representation. Remote Sens. 2014, 6, 8424–8445. [Google Scholar] [CrossRef]
- Dian, Y.; Li, Z.; Pang, Y. Spectral and texture features combined for forest tree species classification with airborne hyperspectral imagery. J. Indian Soc. Remote Sens. 2015, 43, 101–107. [Google Scholar] [CrossRef]
- Szantoi, Z.; Escobedo, F.; Abd-Elrahman, A.; Smith, S.; Pearlstine, L. Analyzing fine-scale wetland composition using high resolution imagery and texture features. Int. J. Appl. Earth Observ. 2013, 23, 204–212. [Google Scholar] [CrossRef]
- National Marine Data and Information Service. Tide Tables, 1st ed.; Ocean Press: Beijing, China, 2016 and 2017; pp. 439–450. ISBN 978-7-5027-9129-2. [Google Scholar]
- Song, C.; Woodcock, C.; Seto, K.; Lenney, M.; Macomber, S. Classification and change detection using Landsat TM data: When and How to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Sun, W.; Chen, B.; Messinger, D. Nearest-neighbor diffusion-based pan-sharpening algorithm for spectral images. Opt. Eng. 2014, 53, 013107. [Google Scholar] [CrossRef] [Green Version]
- Dorado-Munoz, L.; Messinger, D.; Bove, D. Integrating spatial and spectral information for enhancing spatial features in the Gough map of Great Britain. J. Cult. Herit. 2018. Available online: https://www.sciencedirect.com/science/article/pii/S1296207417307008 (accessed on 9 August 2018).
- Zhao, J.; Huang, L.; Yang, H.; Zhang, D.; Wu, Z.; Guo, J. Fusion and assessment of high-resolution WorldView-3 satellite imagery using NNDiffuse and Brovey algorithms. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Chen, D.; Huang, J.; Jackson, T. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Huang, J.; Chen, D.; Cosh, M. Sub-pixel reflectance unmixing in estimating vegetation water content and dry biomass of corn and soybeans cropland using normalized difference water index (NDWI) from satellites. Int. J. Remote Sens. 2009, 30, 2075–2104. [Google Scholar] [CrossRef]
- Wilson, E.; Sader, S. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Onojeghuo, A.; Blackburn, G. Mapping reedbed habitats using texture-based classification of QuickBird imagery. Int. J. Remote Sens. 2011, 32, 8121–8138. [Google Scholar] [CrossRef]
- Mhangara, P.; Odindi, J. Potential of texture-based classification in urban landscapes using multispectral aerial photos. S. Afr. J. Sci. 2013, 109, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Warner, T.; Madden, M.; Atkinson, D. Multi-scale GEOBIA with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Agüera, F.; Aguilar, F.; Aguilar, M. Using texture analysis to improve per-pixel classification of very high resolution images for mapping plastic greenhouses. ISPRS J. Photogram. Remote Sens. 2008, 63, 635–646. [Google Scholar] [CrossRef]
- Pereira, F.; Kampel, M.; Cunha-Lignon, M. Mapping of mangrove forests on the southern coast of São Paulo, Brazil, using synthetic aperture radar data from ALOS/PALSAR. Remote Sens. Lett. 2012, 3, 567–576. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Tsai, F.; Chou, M. Texture augmented analysis of high resolution satellite imagery in detecting invasive plant species. J. Chin. Inst. Eng. 2006, 29, 581–592. [Google Scholar] [CrossRef]
- Coulibaly, L.; Goïta, K. Evaluation of the potential of various spectral indices and textural features derived from satellite images for surficial deposits mapping. Int. J. Remote Sens. 2006, 27, 4567–4584. [Google Scholar] [CrossRef]
- Shaban, M.; Dikshit, O. Improvement of classification in urban areas by the use of textural features: The case study of Lucknow city, Uttar Pradesh. Int. J. Remote Sens. 2001, 22, 565–593. [Google Scholar] [CrossRef]
- Shafri, H.; Ramle, F. A Comparison of Support Vector Machine and Decision Tree Classifications Using Satellite Data of Langkawi Island. Inf. Tech. J. 2009, 8, 64–70. [Google Scholar] [CrossRef]
- Yang, X. Parameterizing support vector machines for land cover classification. Photogram. Eng. Remote Sens. 2011, 77, 27–37. [Google Scholar] [CrossRef]
- Wahidin, N.; Siregar, V.; Nababan, B.; Jaya, I.; Wouthuyzen, S. Object-based image analysis for coral reef benthic habitat mapping with several classification algorithms. Procedia Environ. Sci. 2015, 24, 222–227. [Google Scholar] [CrossRef]
- Mallinis, G.; Koutsias, N.; Tsakiri-Strati, M.; Karteris, M. Object-based classification using Quickbird imagery for delineating forest vegetation polygons in a Mediterranean test site. ISPRS J. Photogram. Remote Sens. 2008, 63, 237–250. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 1st ed.; Springer: New York, NY, USA, 1995; Volume 37, pp. 34–35. [Google Scholar]
- Myint, S.; Giri, C.; Wang, L.; Zhu, Z.; Gillette, S. Identifying Mangrove Species and Their Surrounding Land Use and Land Cover Classes Using an Object-Oriented Approach with a Lacunarity Spatial Measure. GISci. Remote Sens. 2008, 45, 188–208. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Object-based approach for multi-scale mangrove composition mapping using multi-resolution image datasets. Remote Sens. 2015, 7, 4753–4783. [Google Scholar] [CrossRef]
- Nascimento, W., Jr.; Souza-Filho, P.; Proisy, C.; Lucas, R. Mapping changes in the largest continuous Amazonian mangrove belt using object-based classification of multisensor satellite imagery. Estuar. Coast. Shelf Sci. 2013, 117, 83–93. [Google Scholar] [CrossRef]
- Johansen, K.; Phinn, S.; Witte, C.; Philip, S.; Newton, L. Mapping banana plantations from object-oriented classification of SPOT-5 imagery. Photogram. Eng. Remote Sens. 2009, 75, 1069–1081. [Google Scholar] [CrossRef]
- Myint, S.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Akay, M. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 16, 3240–3247. [Google Scholar] [CrossRef]









| Land-Cover Types | Description | |
|---|---|---|
| Mangroves | High-stand mangroves | Areas covered by mangroves which are located on high tidal flats, and not submerged during high tide |
| Low-stand mangroves | Areas covered by mangroves located on low tidal flats and submerged during high tide | |
| Non-mangroves | Tidal flats | Areas covered and exposed by the tides |
| Terrestrial vegetation | Areas covered by forests, farmland, and grassland | |
| Built-up land | Areas covered by artificial facilities | |
| water | Areas covered by water (including ocean and rivers) | |
| Percent Difference | Tidal Flats | High-Stand Mangroves | Low-Stand Mangroves | Terrestrial Vegetation | Built-Up Land | Water |
|---|---|---|---|---|---|---|
| (NIRl − NIRh)/NIRh | 63% | −10.6% | 40.9% | −14.3% | −13.1% | −17.1% |
| Land-Cover Type | NDVIl | NDVIh | NDVIl − NDVIh | (NDVIl − NDVIh) × ((NIRl − NIRh)/NIRh) |
|---|---|---|---|---|
| Tidal flats | −0.0062 | −0.2186 | 0.2124 | 0.1347 |
| High-stand mangroves | 0.6296 | 0.6945 | −0.0649 | 0.0069 |
| Low-stand mangroves | 0.5003 | 0.0812 | 0.4191 | 0.1717 |
| Terrestrial vegetation | 0.6027 | 0.6181 | −0.0154 | 0.0022 |
| Built-up land | 0.1258 | 0.2197 | −0.0939 | 0.0123 |
| Water | −0.3335 | −0.1793 | −0.1542 | 0.0264 |
| Method | Classified Category | Category by Visual Interpretation | Producer Accuracy | User Accuracy | Overall Accuracy | Kappa | Area (ha) | |
|---|---|---|---|---|---|---|---|---|
| Mangroves | Non-Mangroves | |||||||
| SVMl + SMRI | Mangroves | 18 | 2 | 90% | 90% | 94% | 0.86 | 911.95 |
| Non-mangroves | 2 | 46 | 95% | 95% | ||||
| SVMl | Mangroves | 15 | 4 | 75% | 91% | 86% | 0.68 | 860.70 |
| Non-mangroves | 5 | 44 | 79% | 89% | ||||
| SVMh + SMRI | Mangroves | 17 | 3 | 85% | 85% | 91% | 0.79 | 799.27 |
| Non-mangroves | 3 | 45 | 93% | 93% | ||||
| SVMh | Mangroves | 14 | 5 | 70% | 74% | 84% | 0.60 | 594.22 |
| Non-mangroves | 6 | 43 | 89% | 88% | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Q.; Qin, C.-Z.; Li, H.; Huang, C.; Su, F.-Z. Mapping Mangrove Forests Based on Multi-Tidal High-Resolution Satellite Imagery. Remote Sens. 2018, 10, 1343. https://doi.org/10.3390/rs10091343
Xia Q, Qin C-Z, Li H, Huang C, Su F-Z. Mapping Mangrove Forests Based on Multi-Tidal High-Resolution Satellite Imagery. Remote Sensing. 2018; 10(9):1343. https://doi.org/10.3390/rs10091343
Chicago/Turabian StyleXia, Qing, Cheng-Zhi Qin, He Li, Chong Huang, and Fen-Zhen Su. 2018. "Mapping Mangrove Forests Based on Multi-Tidal High-Resolution Satellite Imagery" Remote Sensing 10, no. 9: 1343. https://doi.org/10.3390/rs10091343
APA StyleXia, Q., Qin, C. -Z., Li, H., Huang, C., & Su, F. -Z. (2018). Mapping Mangrove Forests Based on Multi-Tidal High-Resolution Satellite Imagery. Remote Sensing, 10(9), 1343. https://doi.org/10.3390/rs10091343