Evaluating the Potential of ALS Data to Increase the Efficiency of Aboveground Biomass Estimates in Tropical Peat–Swamp Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Forest Inventory Data and Allometric Biomass Model
2.3. ALS Data and Processing
- Outliers were removed using the FilterData tool, considering a window size of 100 and a maximum and minimum ellipsoidal height bound of .
- A digital elevation model (DEM) grid with 1 cell size was created with the GridSurfaceCreate tool which estimates the elevation of each grid cell from the lowest elevation of all points within the cell; if the cell does not contain any points, it is filled by interpolation from the neighbouring cells.
- A canopy height model (CHM) with 1 cell size was created using the CanopyModel tool by interpolating the first ALS pulses and subtracting the DEM elevation of each cell.
- Finally, the ClipData tool was used to obtain the normalized heights by subtraction of the ellipsoidal height of the DEM from the ellipsoidal height of each ALS return.
2.4. Building the Biomass-Link Model
2.5. AGB Estimation
3. Results
3.1. Forest Inventory Results
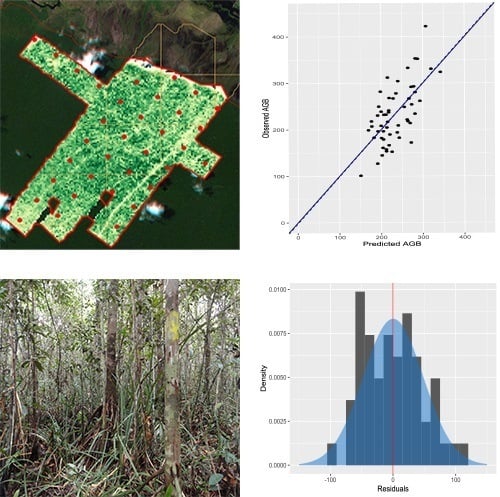
3.2. Biomass-Link Model
3.3. Comparison of the AGB Estimates
4. Discussion
5. Conclusions
- The usage of expensive ALS data in forest monitoring programs cannot always be justified by an actual gain in precision,
- Model-assisted estimators provide a good framework to examine the gain in precision and to evaluate the advantage of using different remote sensing products,
- As different studies report different ’gain’ in precision from using ALS data, further research is required to inform forest monitoring systems on the expected gain of collecting additional remote sensing products before the monitoring is implemented.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy Neotropical forests using lidar remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
- Barrett, F.; Mcroberts, R.E.; Tomppo, E.; Cienciala, E.; Waser, L.T. A questionnaire-based review of the operational use of remotely sensed data by national forest inventories. Remote Sens. Environ. 2016, 174, 279–289. [Google Scholar] [CrossRef]
- Sader, S.A.; Waide, R.B.; Lawrence, W.T.; Joyce, A.T. Tropical forest biomass and successional age class relationships to a vegetation index derived from landsat TM data. Remote Sens. Environ. 1989, 28, 143–198. [Google Scholar] [CrossRef]
- Eckert, S. Improved forest biomass and carbon estimations using texture measures from worldView-2 satellite data. Remote Sens. 2012, 4, 810–829. [Google Scholar] [CrossRef]
- Nichol, J.E.; Sarker, M.L.R. Improved Biomass Estimation Using the Texture Parameters of Two High-Resolution Optical Sensors. IEEE Trans. Geosci. Remote Sens. 2011, 49, 930–948. [Google Scholar] [CrossRef] [Green Version]
- Dobson, M.; Ulaby, F.; LeToan, T.; Beaudoin, A.; Kasischke, E.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small—Footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.; Parker, G.; Shugart, H. Surface Lidar Remote Sensing of Basal Area and Biomass in Deciduous Forests of Eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Short, A.; Valenti, M. Measuring biomass and carbon in delaware using an airborne profiling LIDAR. Scand. J. For. Res. 2004, 19, 500–511. [Google Scholar] [CrossRef]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. Remote Sens. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing—Based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark County, NorwayThis article is one of a selection of papers from Extending Forest Inventory and Monitoring over Space and Time. Can. J. For. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Ståhl, G.; Holm, S.; Gregoire, T.G.; Gobakken, T.; Næsset, E.; Nelson, R. Model-based inference for biomass estimation in a LiDAR sample survey in Hedmark County, Norway. Can. J. of For. Res. 2011, 41, 96–107. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Bollandsås, O.M.; Gregoire, T.G.; Nelson, R.; Ståhl, G. Comparison of precision of biomass estimates in regional field sample surveys and airborne LiDAR-assisted surveys in Hedmark County, Norway. Remote Sens. Environ. 2013, 130, 108–120. [Google Scholar] [CrossRef]
- McRoberts, R.E. A model-based approach to estimating forest area. Remote Sens. Environ. 2006, 103, 56–66. [Google Scholar] [CrossRef]
- Opsomer, J.D.; Breidt, F.J.; Moisen, G.G.; Kauermann, G. Model-assisted estimation of forest resources with generalized additive models. J. Am. Stat. Assoc. 2007, 102, 400–409. [Google Scholar] [CrossRef]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: Berlin, Germany, 1992. [Google Scholar]
- Næsset, E.; Gobakken, T.; Solberg, S.; Gregoire, T.G.; Nelson, R.; Ståhl, G.; Weydahl, D. Model-assisted regional forest biomass estimation using LiDAR and InSAR as auxiliary data: A case study from a boreal forest area. Remote Sens. Environ. 2011, 115, 3599–3614. [Google Scholar] [CrossRef]
- Næsset, E.; Ørka, H.O.; Solberg, S.; Bollandsås, O.M.; Hansen, E.H.; Mauya, E.; Zahabu, E.; Malimbwi, R.; Chamuya, N.; Olsson, H.; et al. Mapping and estimating forest area and aboveground biomass in miombo woodlands in Tanzania using data from airborne laser scanning, TanDEM-X, RapidEye, and global forest maps: A comparison of estimated precision. Remote Sens. Environ. 2016, 175, 282–300. [Google Scholar] [CrossRef]
- D’Oliveira, M.V.N.; Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E. Estimating forest biomass and identifying low-intensity logging areas using airborne scanning lidar in Antimary State Forest, Acre State, Western Brazilian Amazon. Remote Sens. Environ. 2012, 124, 479–491. [Google Scholar] [CrossRef]
- Page, S.E.; Rieley, J.O.; Shotyk, W.; Weiss, D. Interdependence of peat and vegetation in a tropical peat swamp forest. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1999, 354, 1885–1897. [Google Scholar] [CrossRef] [PubMed]
- Ballhorn, U.; Jubanski, J.; Kronseder, K. Airborne LiDAR measurements to estimate tropical peat swamp forest aboveground Biomass. In Proceedings of the International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1660–1663. [Google Scholar]
- Ballhorn, U.; Jubanski, J.; Siegert, F. ICESat/GLAS data as a measurement tool for peatland topography and peat swamp forest biomass in Kalimantan, Indonesia. Remote Sens. 2011, 3, 1957–1982. [Google Scholar] [CrossRef] [Green Version]
- Jubanski, J.; Ballhorn, U.; Kronseder, K.; Franke, J.; Siegert, F. Detection of large above-ground biomass variability in lowland forest ecosystems by airborne LiDAR. Biogeosciences 2013, 10, 3917–3930. [Google Scholar] [CrossRef] [Green Version]
- Kronseder, K.; Ballhorn, U.; Böhm, V.; Siegert, F. aboveground biomass estimation across forest types at different degradation levels in Central Kalimantan using LiDAR data. Int. J. Appl. Earth Obs. Geoinform. 2012, 18, 37–48. [Google Scholar] [CrossRef]
- Hirano, T.; Kusin, K.; Limin, S.; Osaki, M. Carbon dioxide emissions through oxidative peat decomposition on a burnt tropical peatland. Glob. Chang. Biol. 2014, 20, 555–565. [Google Scholar] [CrossRef] [PubMed]
- BMKG. Prakiraan Musim Hujan 2014/2015 di Indonesia; Badan Meteorologi Klimatology dan Geofisika: Jakarta, Indonesia, 2014. [Google Scholar]
- Harrison, M.E. Orang-Utan Feeding Behaviour in Sabangau, Central Kalimatan. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2009. [Google Scholar]
- Campbell, L.A.D. Disturbance Effects on Carbon Content and Tree Species Traits in Tropical Peat Swamp Forest in Central Kalimantan, Indonesian Borneo. Bachelor’s Thesis, Dalhousie University, Halifax, NS, Canada, 2013. [Google Scholar]
- Pérez-Cruzado, C.; Fehrmann, L.; Magdon, P.; Cañellas, I.; Sixto, H.; Kleinn, C. On the site-level suitability of biomass models. Environ. Model. Softw. 2015, 73, 14–26. [Google Scholar] [CrossRef]
- Manuri, S.; Brack, C.; Nugroho, N.P.; Hergoualc’h, K.; Novita, N.; Dotzauer, H.; Verchot, L.; Putra, C.A.S.; Widyasari, E. Tree biomass equations for tropical peat swamp forest ecosystems in Indonesia. For. Ecol. Manag. 2014, 334, 241–253. [Google Scholar] [CrossRef]
- McGaughey, J.R. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; United States Department of Agriculture, Forest Service, Pacific Northwest Research Station, University of Washington: Seattle, WA, USA, 2014. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Kraus, K.; Mikhail, E. Linear least squares interpolation. Photogramm. Eng. 1972, 635, 1016–1029. [Google Scholar]
- Magdon, P.; Purnama, E.; Sarodja, D.; Perez-Cruzado, C. Estimating aboveground biomass using small footprint LiDAR data in tropical peat–swamp forests. -A case study from Central Kalimantan-. In The Ecological and Economic Challanges of Managing Forested Landscapes in a Global Context; Cuvillier Verlag: Göttingen, Germany, 2014. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Gonzalez-Ferreiro, E.; Miranda, D.; Barreiro-Fernandez, L.; Bujan, S.; Garcia-Gutierrez, J.; Dieguez-Aranda, U. Modelling stand biomass fractions in Galician eucalyptus globulus plantations by use of different LiDAR pulse densities. For. Syst. 2013, 22, 510–525. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Walters, B.F. Statistical inference for remote sensing-based estimates of net deforestation. Remote Sens. Environ. 2012, 124, 394–401. [Google Scholar] [CrossRef]
- Kangas, A.; Myllymäki, M.; Gobakken, T.; Næsset, E. Model-assisted forest inventory with parametric, semi-parametric and non-parametric models. Can. J. For. Res. 2016, 868. [Google Scholar] [CrossRef]
- Fuchs, H.; Magdon, P.; Kleinn, C.; Flessa, H. Estimating aboveground carbon in a catchment of the Siberian forest tundra: Combining satellite imagery and field inventory. Remote Sens. Environ. 2009, 113, 518–531. [Google Scholar] [CrossRef]
- Lumley, T. Leaps: Regression Subset Selection. 2009. R Package Version 2.9. Available online: http://CRAN.R-project.org/package=leaps (accessed on 3 August 2018 ).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Ioki, K.; Tsuyuki, S.; Hirata, Y.; Phua, M.H.; Wong, W.V.C.; Ling, Z.Y.; Saito, H.; Takao, G. Estimating above-ground biomass of tropical rainforest of different degradation levels in Northern Borneo using airborne LiDAR. For. Ecol. Manag. 2014, 328, 335–341. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Frate, F.D.; Guerriero, L.; Pirotti, F.; Valentini, R. Aboveground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Domke, G.M.; Ståhl, G.; Saarela, S.; Westfall, J.A. Hybrid estimators for mean aboveground carbon per unit area. For. Ecol. Manag. 2016, 378, 44–56. [Google Scholar] [CrossRef]
- McRoberts, R.E. Satellite image-based maps: Scientific inference or pretty pictures? Remote Sens. Environ. 2011, 115, 715–724. [Google Scholar] [CrossRef]
- Englhart, S.; Jubanski, J.; Siegert, F. Quantifying Dynamics in Tropical Peat Swamp Forest Biomass with Multi-Temporal LiDAR Datasets. Remote Sens. 2013, 5, 2368–2388. [Google Scholar] [CrossRef] [Green Version]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- Slik, J.W.F.; Paoli, G.; Mcguire, K.; Amaral, I.; Barroso, J.; Bastian, M.; Blanc, L.; Bongers, F.; Boundja, P.; Clark, C.; et al. Large trees drive forest aboveground biomass variation in moist lowland forests across the tropics. Glob. Ecol. Biogeogr. 2013, 22, 1261–1271. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef] [Green Version]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Variables Related to Height | |
|---|---|
| Distribution (m) | Description |
| maximum | |
| mean | |
| mode | |
| standard deviation | |
| variance | |
| coefficient of variation | |
| interquartile range | |
| skewness | |
| kurtosis | |
| average absolute deviation | |
| median of the absolute deviations from the overall median | |
| median of the absolute deviations from the overall mode | |
| L-moments | |
| L-moment skewness | |
| L-moment kurtosis | |
| L-moment coefficient of variation | |
| percentiles | |
| Quadratic mean | |
| Cubic mean | |
| Variables Related to | |
| Canopy Closure | Description |
| ratio of the number of the first laser returns above to the number of first laser returns for each plot | |
| ratio of the number of the first laser returns above to the number of first returns for each plot | |
| ratio of the number of the all laser returns above to the number of all laser returns for each plot | |
| ratio of the number of the all laser returns above to the number of all laser returns for each plot | |
| ratio of the number of the first laser returns above 6 meter height to the total number of first laser returns for each plot | |
| ratio of the number of the all laser returns above 6 height to the total number of first laser returns for each plot | |
| Canopy relief ratio ((mean−min)/(max−min)) |
| Target Variable | Mean | Minimum | Maximum | CV % |
|---|---|---|---|---|
| Mean DBH () | 18.7 | 11.1 | 25 | 20.2 |
| Mean Height () | 17.4 | 10.6 | 23.2 | 16.5 |
| Basal Area ( −1) | 30.2 | 17.5 | 42.2 | 22.9 |
| Stems per ha | 2166 | 1069 | 4824 | 33.3 |
| AGB ( −1) | 241.4 | 100.9 | 352.8 | 27.0 |
| Estimator | n | N | ||||
|---|---|---|---|---|---|---|
| field-based | 34 | – | 241.38 | 124.81 | 11.17 | 4.63% |
| ALS-assisted | 34 | 9480 | 245.08 | 111.66 | 10.57 | 4.30% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magdon, P.; González-Ferreiro, E.; Pérez-Cruzado, C.; Purnama, E.S.; Sarodja, D.; Kleinn, C. Evaluating the Potential of ALS Data to Increase the Efficiency of Aboveground Biomass Estimates in Tropical Peat–Swamp Forests. Remote Sens. 2018, 10, 1344. https://doi.org/10.3390/rs10091344
Magdon P, González-Ferreiro E, Pérez-Cruzado C, Purnama ES, Sarodja D, Kleinn C. Evaluating the Potential of ALS Data to Increase the Efficiency of Aboveground Biomass Estimates in Tropical Peat–Swamp Forests. Remote Sensing. 2018; 10(9):1344. https://doi.org/10.3390/rs10091344
Chicago/Turabian StyleMagdon, Paul, Eduardo González-Ferreiro, César Pérez-Cruzado, Edwine Setia Purnama, Damayanti Sarodja, and Christoph Kleinn. 2018. "Evaluating the Potential of ALS Data to Increase the Efficiency of Aboveground Biomass Estimates in Tropical Peat–Swamp Forests" Remote Sensing 10, no. 9: 1344. https://doi.org/10.3390/rs10091344
APA StyleMagdon, P., González-Ferreiro, E., Pérez-Cruzado, C., Purnama, E. S., Sarodja, D., & Kleinn, C. (2018). Evaluating the Potential of ALS Data to Increase the Efficiency of Aboveground Biomass Estimates in Tropical Peat–Swamp Forests. Remote Sensing, 10(9), 1344. https://doi.org/10.3390/rs10091344