A Microwave Tomography Strategy for Underwater Imaging via Ground Penetrating Radar
Abstract
:1. Introduction
- (i)
- adoption of the Born approximation, which permits to formulate the imaging as a linear inverse problem;
- (ii)
- assumption that the materials are non-magnetic and lossless, specifically the material dispersive behavior is neglected in order to exploit frequency diversity of data;
- (iii)
- use of a two dimensional and ray-based model (by considering that the transmitting/receiving antennas are far, in terms of probing wavelength, from the water bottom) to express in a simple way the incident field and the Green’s function, which are the key elements of the mathematical relationship between data and unknown of the problem at hand; and
- (iv)
- introduction of an equivalent relative dielectric permittivity, from now on simply referred as equivalent permittivity, whose value depends on the distance of the antenna from the water-medium interface and the depth of the generic point into the investigation domain.
2. Data Processing Approach
2.1. Pre-Processing
2.2. Data Inversion
- The wave-material interaction is described according to the Born approximation, thus, the imaging is faced as a linear inverse scattering problem [34];
- The dispersive behavior of the materials involved in the scattering phenomenon is neglected and hence the contrast function does not change with the frequency;
- The transmitting and receiving antennas are considered in far-field zone with respect to the investigated area in terms of the probing wavelength;
- The targets are supposed to be far from the freshwater-wet sand interface in terms of the underground probing wavelength; and
- The propagation is described by means of an equivalent wave number , where is the wavenumber in air [30].
3. GPR Surveys and Results
3.1. Experimental Test Site and Instrumentation Description
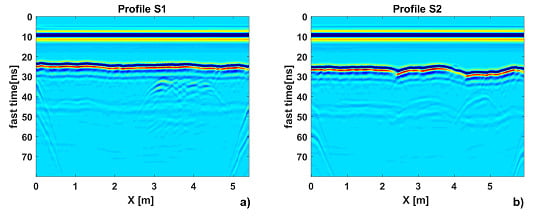
3.2. Results
- (i)
- homogeneous scenario with the relative dielectric permittivity of freshwater ;
- (ii)
- homogeneous scenario with the relative dielectric permittivity of wet sand ; and
- (iii)
- inversion model based on spatially equivalent permittivity .
4. Discussion
5. Conclusions
- (i)
- the layered structure of the reference scenario is taken into account without increasing the complexity of the imaging problem, which is the same of that encountered when the signal propagation occurs in a homogeneous medium;
- (ii)
- the bathymetry profile is reconstructed from the GPR data; and
- (iii)
- proper estimation of the vertical upper side location and horizontal size of the targets.
Author Contributions
Funding
Conflicts of Interest
References
- Daniels, D.J. Ground Penetrating Radar. In IEE Radar, Sonar and Navigation Series 15; IEE: London, UK, 2004. [Google Scholar] [Green Version]
- Persico, R. Introduction to Ground Penetrating Radar: Inverse Scattering and Data Processing; Wiley-IEEE Press: London, UK, 2014. [Google Scholar]
- Conyers, L.B.; Goodman, D. Ground-Penetrating Radar: An Introduction for Archaeologists; AltaMira Press: Walnut Creek, CA, USA, 1997. [Google Scholar]
- Masini, N.; Capozzoli, L.; Chen, P.; Chen, F.; Romano, G.; Lu, P.; Tang, P.; Sileo, M.; Ge, Q.; Lasaponara, R. Towards an Operational Use of Geophysics for Archaeology in Henan (China): Methodological Approach and Results in Kaifeng. Remote Sens. 2017, 9, 809. [Google Scholar] [CrossRef]
- Rizzo, E.; Santoriello, A.; Capozzoli, L.; De Martino, G.; De Vita, C.B.; Musmeci, D.; Perciante, F. Geophysical survey and archaeological data at Masseria Grasso (Benevento, Italy). Surv. Geophys. 2018. [Google Scholar] [CrossRef]
- Capozzoli, L.; Rizzo, E. Combined NDT techniques in civil engineering applications: Laboratory and real tests. Constr. Build. Mater. 2017, 154, 1139–1150. [Google Scholar] [CrossRef]
- Beben, D.; Mordak, A.; Anigacz, W. Identification of viaduct beam parameters using the Ground Penetrating Radar (GPR) technique. NDT E Int. 2012, 49, 18–26. [Google Scholar] [CrossRef]
- De Chiara, F.; Fontul, S.; Fortunato, E. GPR Laboratory Tests for Railways Materials Dielectric Properties Assessment. Remote Sens. 2014, 6, 9712–9728. [Google Scholar] [CrossRef]
- Orlando, L.; Pezone, A.; Colucci, A. Modeling and testing of high frequency GPR data for evaluation of structural deformation. NDT E Int. 2010, 43, 216–230. [Google Scholar] [CrossRef]
- Catapano, I.; Ludeno, G.; Soldovieri, F.; Tosti, F.; Padeletti, G. Structural Assessment via Ground Penetrating Radar at the Consoli Palace of Gubbio (Italy). Remote Sens. 2017, 10, 45. [Google Scholar] [CrossRef]
- Hellsten, H. CARABAS—An UWB low frequency SAR. In Proceedings of the IEEE MTT-S International Symposium, Albuquerque, NM, USA, 1–5 June 1992; Volume 3, pp. 1495–1498. [Google Scholar]
- Catapano, I.; Crocco, L.; Krellmann, Y.; Triltzsch, G.; Soldovieri, F. A tomographic approach for helicopter-borne ground penetrating radar imaging. IEEE Geosci. Remote Sens. Lett. 2012, 9, 378–382. [Google Scholar] [CrossRef]
- Papa, C.; Alberti, G.; Salzillo, G.; Palmese, G.; Califano, D.; Ciofaniello, L.; Daniele, M.; Facchinetti, C.; Longo, F.; Formaro, R.; et al. Design and Validation of a Multimode Multifrequency VHF/UHF Airborne Radar. IEEE. Geosci. Remote Sens. Lett. 2014, 11, 1260–1264. [Google Scholar] [CrossRef]
- Ludeno, G.; Catapano, I.; Renga, A.; Rodi Vetrella, A.; Fasano, G.; Soldovieri, F. Assessment of a micro-UAV system for microwave tomography radar imaging. Remote Sens. Environ. 2018, 212, 90–102. [Google Scholar] [CrossRef]
- Eisenburger, D.; Krellmann, Y.; Lentz, H.; Triltzsch, G. Stepped frequency radar system in gating mode: An experiment as a new helicopter-borne GPR systems for geological applications. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. I153–I156. [Google Scholar]
- Travassos, J.D.M.; Menezes, P.D.T.L. GPR exploration for groundwater in a crystalline rock terrain. J. Appl. Geophys. 2004, 55, 239–248. [Google Scholar] [CrossRef]
- Machguth, H.; Eisen, O.; Paul, F.; Hoelzle, M. Strong spatial variability of snow accumulation observed with helicopter-borne GPR on two adjacent Alpine glaciers. Geophys. Res. Lett. 2006, 33, L13. [Google Scholar] [CrossRef]
- Negi, H.S.; Snehmani, N.T.; Sharma, J.K. Estimation of snow depth and detection of buried objects using airborne ground penetrating radar in Indian Himalaya. Curr. Sci. 2008, 94, 865–870. [Google Scholar]
- Catapano, I.; di Napoli, R.; Soldovieri, F.; Bavusi, M.; Loperte, A.; Dumoulin, J. Structural monitoring via microwave tomography-enhanced GPR: The Montagnole test site. J. Geophys. Eng. 2012, 9, S100. [Google Scholar] [CrossRef]
- Hasan, I.; Yazdani, N. Ground penetrating radar utilization in exploring inadequate concrete covers in a new bridge deck. Case Stud. Constr. Mater. 2014, 1, 104–114. [Google Scholar] [CrossRef]
- Chang, C.W.; Lin, C.H.; Lien, H.S. Measurement radius of reinforcing steel bar in concrete using digital image GPR. Constr. Build. Mater. 2009, 23, 1057–1063. [Google Scholar] [CrossRef]
- Hugenschmidt, J.; Mäder, A. GPR investigation of remains of pile dwellings in Lake Zurich. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–4. [Google Scholar]
- The Impacts of Climate Change on World Heritage Properties. Available online: https:\\whc.unesco.org\document\7041 (accessed on 31 August 2018).
- Xu, X.; Wu, J.; Shen, J.; He, Z. Case Study: Application of GPR to Detection of Hidden Dangers to Underwater Hydraulic Structures. J. Hydraul. Eng. 2006, 1, 12–20. [Google Scholar] [CrossRef]
- Diamanti, N.; Giannopoulos, A.; Forde, M.C. Numerical modelling and experimental verification of GPR to investigate ring separation in brick masonry arch bridges. NDT E Int. 2008, 41, 354–363. [Google Scholar] [CrossRef]
- Soldovieri, F.; Hugenschmidt, J.; Persico, R.; Leone, G. A linear inverse scattering algorithm for realistic GPR applications. Near Surf. Geophys. 2007, 5, 29–42. [Google Scholar] [CrossRef]
- Catapano, I.; Affinito, A.; Gennarelli, G.; di Maio, F.; Loperte, A.; Soldovieri, F. Full three-dimensional imaging via ground penetrating radar: Assessment in controlled conditions and on field for archaeological prospecting. Appl. Phys. A 2013, 115, 1415–1422. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Fortuny-Guasch, J. 3-D radar imaging using range migration techniques. IEEE Trans. Antennas Propag. 2000, 48, 728–737. [Google Scholar] [CrossRef]
- Soldovieri, F.; Crocco, L. Electromagnetic Tomography. In Vertiy Subsurface Sensing; Ahmet, S., Turk Koksal, A., Hocaoglu Alexey, A., Eds.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Catapano, I.; Ludeno, G.; Soldovieri, F. An approximated imaging approach for GPR surveys with antennas far from the interface. In Proceedings of the 2017 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Edinburgh, UK, 28–30 June 2017; pp. 1–5. [Google Scholar]
- Leone, G.; Soldovieri, F. Analysis of the Distorted Born Approximation for Subsurface Reconstruction: Truncation and Uncertainties Effects. IEEE Trans. Geosci. Remote Sens. 2003, 41, 66–74. [Google Scholar] [CrossRef]
- Capozzoli, L.; Caputi, A.; De Martino, G.; Giampaolo, V.; Luongo, R.; Perciante, F.; Rizzo, E. Electrical and electromagnetic techniques applied to an archaeological framework reconstructed in laboratory. In Proceedings of the 2015 8th IEEE IWAGPR, Advanced Ground Penetrating Radar, Florence, Italy, 7–10 July 2015. [Google Scholar]
- Bertero, M.; Boccacci, P. Introduction to Inverse Problems in Imaging; Institute of Physics Publications: London, UK, 1998. [Google Scholar]
- Felsen, L.B.; Marcuvitz, N. Radiation and Scattering of Waves; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Balanis, A.C. Advanced Engineering Electromagnetics; John Wiley & Sons: New York, NY, USA, 2012; Volume 111. [Google Scholar]
- Capozzoli, L.; De Martino, G.; Perciante, F.; Rizzo, E. Geophysical techniques applied to investigate underwater structures. In Proceedings of the 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR), Edinburgh, UK, 28–30 June 2017; pp. 1–5. [Google Scholar]
- Pettinelli, E.; Di Matteo, A.; Mattei, E.; Crocco, L.; Soldovieri, F.; Redman, J.D.; Annan, A.P. GPR Response From Buried Pipes: Measurement on Field Site and Tomographic Reconstructions. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2639–2645. [Google Scholar] [CrossRef]
- Persico, R.; Bernini, R.; Soldovieri, F. The Role of the Measurement Configuration in Inverse Scattering From Buried Objects under the Born Approximation. IEEE Trans. Antennas Propag. 2005, 53, 1875–1887. [Google Scholar] [CrossRef]














| Chemical Results | ||||||
|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | Fe2O3 | CaO | K2O | ||
| % | 93.00 | 2.50 | 0.60 | 1.50 | 1.15 | |
| Particle Size Characteristics d (mm) | ||||||
| d (mm) | 1–0.5 | 0.50–0.25 | 0.250–0.125 | 0.125–0.063 | 0.063–0.032 | >0.032 |
| % | 0.00 | 0.14 | 3.70 | 86.34 | 7.92 | 1.08 |
| Hydrogeological Properties | ||||||
| dm (mm) | Kmax (m/s) | ρ (%) | ||||
| 0.09 | 4 × 10−5 | 45–50 | ||||
| Profile S1 | Profile S2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Paved Road | Wall | Tomb 1 | Tomb 2 | Amphora | ||||||
| zt (m) | (m) | zt (m) | (m) | zt (m) | (m) | zt (m) | (m) | zt (m) | (m) | |
| Ground-truth | 0.77 | 1.45 | 0.55 | 1.71 | 0.95 | 1.44 | 0.99 | 0.94 | 0.80 | 0.28 |
| 0.58 | 0.85 | 0.40 | 1.37 | 0.60 | 0.56 | 0.57 | 0.59 | 0.54 | 0.24 | |
| 1.06 | 0.80 | 0.75 | 1.40 | 1.05 | 0.70 | 1.00 | 0.37 | 1.00 | 0.45 | |
| 0.78 | 0.96 | 0.52 | 1.30 | 0.86 | 1.24 | 0.77 | 0.86 | 0.74 | 0.34 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ludeno, G.; Capozzoli, L.; Rizzo, E.; Soldovieri, F.; Catapano, I. A Microwave Tomography Strategy for Underwater Imaging via Ground Penetrating Radar. Remote Sens. 2018, 10, 1410. https://doi.org/10.3390/rs10091410
Ludeno G, Capozzoli L, Rizzo E, Soldovieri F, Catapano I. A Microwave Tomography Strategy for Underwater Imaging via Ground Penetrating Radar. Remote Sensing. 2018; 10(9):1410. https://doi.org/10.3390/rs10091410
Chicago/Turabian StyleLudeno, Giovanni, Luigi Capozzoli, Enzo Rizzo, Francesco Soldovieri, and Ilaria Catapano. 2018. "A Microwave Tomography Strategy for Underwater Imaging via Ground Penetrating Radar" Remote Sensing 10, no. 9: 1410. https://doi.org/10.3390/rs10091410
APA StyleLudeno, G., Capozzoli, L., Rizzo, E., Soldovieri, F., & Catapano, I. (2018). A Microwave Tomography Strategy for Underwater Imaging via Ground Penetrating Radar. Remote Sensing, 10(9), 1410. https://doi.org/10.3390/rs10091410