A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas
2.2. Data Collection and Preprocessing
2.2.1. Landsat 8 OLI/TIRS Imagery
2.2.2. Lidar Dataset Processing
2.3. SUHI Measurement
2.4. OLS and GWR Analysis
2.5. Derivation and Selection of Explanatory Variables
2.5.1. Land Use/Land Cover Composition (LULC) Variables
2.5.2. Landscape Pattern Metrics
2.5.3. Terrain Factors: Elevation and Northness
3. Results
3.1. LST Spatial Distribution
3.2. Diagnostics of the Regression Models
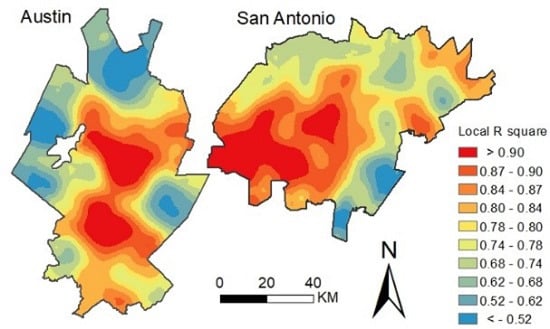
3.3. The Global and Spatial Non-Stationarity Relationship
4. Discussion
4.1. Which Underlying Properties Are Significantly Related to the SUHI for Austin and San Antonio?
4.2. Compared to the Conventional Regression Model, Does the GWR Provide Fresh Insight into the SUHI Phenomenon?
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Coomes, O.T.; Dirzo, R.; Fischer, G.; Folke, C. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Zhou, Y.; Wu, J. How much of the world’s land has been urbanized, really? A hierarchical framework for avoiding confusion. Landsc. Ecol. 2014, 29, 763–771. [Google Scholar] [CrossRef]
- United Nations. World Urbanization Prospects: The 2014 Revision. Erscheinungsort Nicht Ermittelbar United Nations s.l.; United Nations: New York, NY, USA, 2014; Available online: http://www.worldcat.org/title/world-urbanization-prospects-the-2014-revision-highlights/oclc/993940509 (accessed on 28 August 2018).
- Chen, Y.-C.; Chiu, H.-W.; Su, Y.-F.; Wu, Y.-C.; Cheng, K.-S. Does urbanization increase diurnal land surface temperature variation? Evidence and implications. Landsc. Urban Plan. 2017, 157, 247–258. [Google Scholar] [CrossRef]
- Oliveira, E.; Tobias, S.; Hersperger, A. Can strategic spatial planning contribute to land degradation reduction in urban regions? State of the art and future research. Sustainability 2018, 10, 949. [Google Scholar] [CrossRef]
- Zhao, C.; Jensen, J.; Zhan, B. A comparison of urban growth and their influencing factors of two border cities: Laredo in the US and Nuevo Laredo in Mexico. Appl. Geogr. 2017, 79, 223–234. [Google Scholar] [CrossRef]
- Hersperger, A.M.; Oliveira, E.; Pagliarin, S.; Palka, G.; Verburg, P.; Bolliger, J.; Grădinaru, S. Urban land-use change: The role of strategic spatial planning. Glob. Environ. Chang. 2018, 51, 32–42. [Google Scholar] [CrossRef]
- Howard, L. The Climate of London: Deduced from Meteorological Observations, Made at Different Places in The Neighbourhood of the Metropolis: 1818; Volume. 1. Available online: https://archive.org/details/climatelondon00howagoog (accessed on 6 September 2018).
- Zhou, D.; Zhao, S.; Zhang, L.; Liu, S. Remotely sensed assessment of urbanization effects on vegetation phenology in China’s 32 major cities. Remote Sens. Environ. 2016, 176, 272–281. [Google Scholar] [CrossRef]
- Sarrat, C.; Lemonsu, A.; Masson, V.; Guedalia, D. Impact of urban heat island on regional atmospheric pollution. Atmos. Environ. 2006, 40, 1743–1758. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Huang, Q.; Lu, Y. The effect of urban heat island on climate warming in the Yangtze river delta urban agglomeration in china. Int. J. Environ. Res. Public Health 2015, 12, 8773–8789. [Google Scholar] [CrossRef] [PubMed]
- Harlan, S.L.; Brazel, A.J.; Jenerette, G.D.; Jones, N.S.; Larsen, L.; Prashad, L.; Stefanov, W.L. In the shade of affluence: The inequitable distribution of the urban heat island. Res. Soc. Prob. Public Policy 2007, 15, 173–202. [Google Scholar]
- Nichol, J.E. High-resolution surface temperature patterns related to urban morphology in a tropical city: A satellite-based study. J. Appl. Meteorol. 1996, 35, 135–146. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2009, 25, 17–33. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Chen, X.-L.; Zhao, H.-M.; Li, P.-X.; Yin, Z.-Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Jiang, Y.; Fu, P.; Weng, Q. Assessing the impacts of urbanization-associated land use/cover change on land surface temperature and surface moisture: A case study in the midwestern United States. Remote Sens. 2015, 7, 4880–4898. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T. Landscape configuration and urban heat island effects: Assessing the relationship between landscape characteristics and land surface temperature in phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, china. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Peng, J.; Xie, P.; Liu, Y.; Ma, J. Urban thermal environment dynamics and associated landscape pattern factors: A case study in the Beijing metropolitan region. Remote Sens. Environ. 2016, 173, 145–155. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Xiao, R.; Chen, Y.; Liu, X.; Zhang, X. Impacts of urban biophysical composition on land surface temperature in urban heat island clusters. Landsc. Urban Plan. 2015, 135, 1–10. [Google Scholar] [CrossRef]
- Xian, G.; Crane, M. An analysis of urban thermal characteristics and associated land cover in Tampa bay and Las Vegas using landsat satellite data. Remote Sens. Environ. 2006, 104, 147–156. [Google Scholar] [CrossRef]
- Zheng, B.; Myint, S.W.; Fan, C. Spatial configuration of anthropogenic land cover impacts on urban warming. Landsc. Urban Plan. 2014, 130, 104–111. [Google Scholar] [CrossRef]
- Myint, S.W.; Zheng, B.; Talen, E.; Fan, C.; Kaplan, S.; Middel, A.; Smith, M.; Huang, H.-P.; Brazel, A. Does the spatial arrangement of urban landscape matter? Examples of urban warming and cooling in phoenix and Las Vegas. Ecosyst. Health Sustain. 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Deilami, K.; Kamruzzaman, M.; Hayes, J. Correlation or causality between land cover patterns and the urban heat island effect? Evidence from Brisbane, Australia. Remote Sens. 2016, 8, 716. [Google Scholar] [CrossRef]
- Fan, C.; Rey, S.J.; Myint, S.W. Spatially filtered ridge regression (sfrr): A regression framework to understanding impacts of land cover patterns on urban climate. Trans. GIS 2017, 21, 862–879. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Miaomiao, X.; Wang, Y. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression. Environ. Model. Softw. 2010, 25, 1789–1800. [Google Scholar] [CrossRef]
- Ivajnšič, D.; Kaligarič, M.; Žiberna, I. Geographically weighted regression of the urban heat island of a small city. Appl. Geogr. 2014, 53, 341–353. [Google Scholar] [CrossRef]
- Luo, X.; Peng, Y. Scale effects of the relationships between urban heat islands and impact factors based on a geographically-weighted regression model. Remote Sens. 2016, 8, 760. [Google Scholar] [CrossRef]
- Li, W.; Cao, Q.; Lang, K.; Wu, J. Linking potential heat source and sink to urban heat island: Heterogeneous effects of landscape pattern on land surface temperature. Sci. Total Environ. 2017, 586, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Wu, Z. Land surface temperature retrieval from landsat 8 tirs—Comparison between radiative transfer equation-based method, split window algorithm and single channel method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from landsat tm 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Caselles, V.; Becker, F. Significance of the remotely sensed thermal infrared measurements obtained over a citrus orchard. ISPRS J. Photogramm. Remote Sens. 1990, 44, 343–354. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Isaya Ndossi, M.; Avdan, U. Application of open source coding technologies in the production of land surface temperature (lst) maps from landsat: A pyqgis plugin. Remote Sens. 2016, 8, 413. [Google Scholar] [CrossRef]
- Guo, L.; Ma, Z.; Zhang, L. Comparison of bandwidth selection in application of geographically weighted regression: A case study. Can. J. For. Res. 2008, 38, 2526–2534. [Google Scholar] [CrossRef]
- Nakaya, T. Geographically weighted generalised linear modelling. In Geocomputation: A Practical Primer; Chris, B., Alex, S., Eds.; Sage Publication: Thousand Oaks, CA, USA, 2015; pp. 217–220. [Google Scholar]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 national land cover database for the conterminous united states–representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Wickham, J.; Stehman, S.V.; Gass, L.; Dewitz, J.A.; Sorenson, D.G.; Granneman, B.J.; Poss, R.V.; Baer, L.A. Thematic accuracy assessment of the 2011 national land cover database (nlcd). Remote Sens. Environ. 2017, 191, 328–341. [Google Scholar] [CrossRef]
- Zhao, C.; Jensen, J.; Weng, Q.; Currit, N.; Weaver, R. Application of airborne remote sensing data on mapping Local Climate Zones: cases of three metropolitan areas of Texas, U.S. Comput. Environ. Urban Syst. 2018. under review. [Google Scholar]
- Khandelwal, S.; Goyal, R.; Kaul, N.; Mathew, A. Assessment of land surface temperature variation due to change in elevation of area surrounding Jaipur, India. Egypt. J. Remote Sens. Space Sci. 2017, 21, 87–94. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Yue, W.; Xu, J.; Tan, W.; Xu, L. The relationship between land surface temperature and ndvi with remote sensing: Application to shanghai landsat 7 etm+ data. Int. J. Remote Sens. 2007, 28, 3205–3226. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Xiong, Z.; Wang, Y.-C.; Guo, L. Quantifying the multilevel effects of landscape composition and configuration on land surface temperature. Remote Sens. Environ. 2016, 178, 84–92. [Google Scholar] [CrossRef]
- Kim, J.H.; Gu, D.; Sohn, W.; Kil, S.H.; Kim, H.; Lee, D.K. Neighborhood landscape spatial patterns and land surface temperature: An empirical study on single-family residential areas in Austin, Texas. Int. J. Environ. Res. Public Health 2016, 13, 880. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Du, S.; Feng, X.; Guo, L. The relationships between landscape compositions and land surface temperature: Quantifying their resolution sensitivity with spatial regression models. Landsc. Urban Plan. 2014, 123, 145–157. [Google Scholar] [CrossRef]
- Wang, J.; Qingming, Z.; Guo, H.; Jin, Z. Characterizing the spatial dynamics of land surface temperature–impervious surface fraction relationship. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 55–65. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, Q.; Ouyang, W. Impact of urban climate landscape patterns on land surface temperature in wuhan, china. Sustainability 2017, 9, 1700. [Google Scholar] [CrossRef]
- Krayenhoff, E.S.; Voogt, J.A. Daytime thermal anisotropy of urban neighbourhoods: Morphological causation. Remote Sens. 2016, 8, 108. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Hénon, A.; Kurz, B.; Moreau, P.; Irvine, M.; Voogt, J.; Mestayer, P. Modelling daytime thermal infrared directional anisotropy over Toulouse city centre. Remote Sens. Environ. 2010, 114, 87–105. [Google Scholar] [CrossRef]








| Areas | Location (the Center Point) 1 | Land Area (Square km2) 1 | Estimated Population (1 July 2015) 2 | Bare Earth Elevation (Approximate, meters) 3 | Average Temperature Range (°C), July 4 | Average Precipitation (mm), July 4 |
|---|---|---|---|---|---|---|
| Austin | 30.36°N, 97.78°W | 4587.36 | 931,830 | (107, 405) Mean: 235 | (23.6, 35.3) | 48 |
| San Antonio | 32.76°N, 96.97°W | 4752.04 | 1,469,845 | (116, 579) Mean: 263 | (23.3, 34.8) | 52 |
| Projects | Point Space and MSE Accuracy (Horizontal/Vertical, cm) | Datum (Horizontal/Vertical) and Projection | Point Classes |
|---|---|---|---|
| CAPCOG 2007 Caldwell, Travis, Williamson | 140; 100/18.5 | NAD83/NAVD88; State Plane Texas Central | Ground/unclassified |
| CAPCOG 2008 Bastrop, Fayette, Hays | 140; 100/18.5–37 | NAD83/NAVD88; State Plane Texas South Central | Ground/unclassified |
| CAPCOG 2012 Travis | 140; N/A | NAD83/NAVD88; State Plane Texas Central | 1, 2, 3, 4, 5, 6, 7, 9, 11, 15, 17 |
| FEMA 2011 Comal, Guadalupe | 100; 60/12.5 | NAD83, NSRS2007/NAVD88, Geoid 09; UTM Zone 14N | 1, 2, 7, 9 ,10, 11 |
| StratMap 2010 Bexar | 50; 100/19 | NAD83/NAVD88, Geoid 09; UTM Zone 14N | 1, 2, 6, 7, 9, 12, 13 |
| StratMap 2011 Caldwell, Gonzales | 50; 75/15 | NAD83/NAVD88, Geoid 09; UTM Zone 14N | 1, 2, 4, 6, 7, 9, 13 |
| Variables | Derivation Sources | Max. | Min. | Mean | SD | |
|---|---|---|---|---|---|---|
| Land use/land cover composition (LULC) variables | ||||||
| Canopy (Tree Canopy Fraction) | 2011 NLCD Tree Canopy dataset | Austin | 87.46 | 1.26 | 32.89 | 19.83 |
| San Antonio | 86.48 | 0.46 | 32.30 | 20.00 | ||
| ISF (Impervious Surfaces Fraction) | 2011 NLCD ISF dataset | Austin | 80.83 | 0.00 | 9.44 | 14.25 |
| San Antonio | 86.42 | 0.00 | 12.12 | 17.10 | ||
| BF (Buildings fraction) | Building footprints | Austin | 43.96 | 0.00 | 5.07 | 8.43 |
| San Antonio | 51.25 | 0.00 | 5.52 | 8.72 | ||
| NDVI (Normalized Difference Vegetation Index) | Landsat 8 OLI, 20 July 2015 | Austin | 0.53 | −0.44 | 0.31 | 0.10 |
| San Antonio | 0.57 | −0.38 | 0.30 | 0.10 | ||
| Landscape pattern metrics variables | ||||||
| CONTAG (Contagion Index) | NLCD LULC data | Austin | 87.34 | 10.68 | 40.76 | 11.08 |
| San Antonio | 97.90 | 10.18 | 41.67 | 11.90 | ||
| PD (Patch Density) | – | Austin | 137.22 | 4.56 | 53.83 | 30.26 |
| San Antonio | 128.74 | 0.65 | 53.51 | 30.88 | ||
| SHDI (Shannon’s Diversity Index) | – | Austin | 2.42 | 0.25 | 1.54 | 0.33 |
| San Antonio | 2.34 | 0.02 | 1.49 | 0.36 | ||
| PR (Patch Richness) | – | Austin | 15.00 | 3.00 | 8.65 | 2.12 |
| San Antonio | 15.00 | 2.00 | 8.46 | 2.48 | ||
| Terrain variables | ||||||
| Elevation | Aggregated from 5 m × 5 m DTMs | Austin | 403.51 | 113.14 | 227.66 | 56.95 |
| San Antonio | 526.87 | 124.96 | 255.19 | 75.88 | ||
| Northness | Aggregated from 5 m × 5 m Northness dataset | Austin | 0.48 | −0.66 | −0.04 | 0.13 |
| San Antonio | 0.93 | −0.67 | −0.06 | 0.14 | ||
| Austin | San Antonio | |||||||||
| Global Regression | GWR | Global Regression | GWR | |||||||
| β | S.E. | t | Mean β | SD | β | S.E. | t | Mean β | SD | |
| SHDI | 0.04 *** | 0.013 | 3.38 | 0.04 | 0.09 | 0.01 | 0.007 | 1.24 | −0.01 | 0.07 |
| BF | 0.29 *** | 0.010 | 29.50 | 0.28 | 0.23 | 0.19 *** | 0.007 | 27.42 | 0.13 | 0.14 |
| NDVI | −0.74 *** | 0.018 | −41.08 | −0.83 | 0.46 | −0.38 *** | 0.011 | −33.66 | −0.48 | 0.14 |
| Elevation | 0.20 *** | 0.010 | 20.35 | 0.18 | 0.20 | 0.09 *** | 0.006 | 14.05 | 0.09 | 0.36 |
| Northness | −0.15 *** | 0.016 | −9.41 | −0.09 | 0.10 | −0.23 *** | 0.013 | −18.59 | −0.07 | 0.10 |
| Intercept | 104.46 *** | 1.935 | 53.97 | 109.41 | 40.04 | 104.62 *** | 1.154 | 90.68 | 109.29 | 14.87 |
| Diagnostics | ||||||||||
| Residual sum of squares | 476,925.15 | 137,817.06 | 194,028.74 | 55,084.50 | ||||||
| −2 Log likelihood | 29,726.22 | 24,900.77 | 27,523.09 | 22,344.25 | ||||||
| Classic AIC | 29,740.22 | 25,254.64 | 27,537.09 | 22,700.98 | ||||||
| AICc | 29,740.25 | 25,271.62 | 27,537.12 | 22,717.25 | ||||||
| CV | 123.72 | 39.71 | 47.37 | 14.70 | ||||||
| R square | 0.53 | 0.86 | 0.45 | 0.84 | ||||||
| Adjusted R square | 0.53 | 0.85 | 0.45 | 0.84 | ||||||
| Global Moran’s I | 0.440 *** | 0.058 *** | 0.745 *** | 0.516 *** | ||||||
| Bandwidth of GWR | 52.00 | 52.00 | ||||||||
| F-tests of improvement | 36.42 *** | 39.20 *** | ||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Jensen, J.; Weng, Q.; Weaver, R. A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon. Remote Sens. 2018, 10, 1428. https://doi.org/10.3390/rs10091428
Zhao C, Jensen J, Weng Q, Weaver R. A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon. Remote Sensing. 2018; 10(9):1428. https://doi.org/10.3390/rs10091428
Chicago/Turabian StyleZhao, Chunhong, Jennifer Jensen, Qihao Weng, and Russell Weaver. 2018. "A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon" Remote Sensing 10, no. 9: 1428. https://doi.org/10.3390/rs10091428
APA StyleZhao, C., Jensen, J., Weng, Q., & Weaver, R. (2018). A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon. Remote Sensing, 10(9), 1428. https://doi.org/10.3390/rs10091428