Figure 1.
Fully convolutional neural network architecture (FCN-8).
Figure 1.
Fully convolutional neural network architecture (FCN-8).
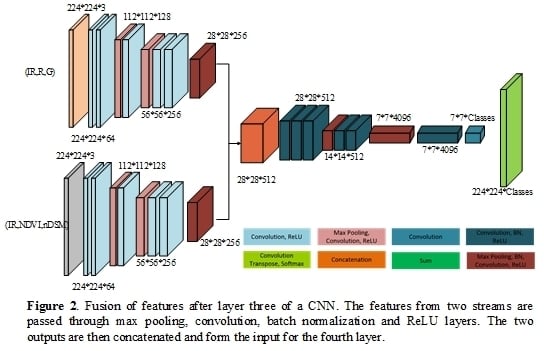
Figure 2.
Fusion of features after layer three of a CNN. The features from two streams are passed through max pooling, convolution, batch normalization and ReLU layers. The two outputs are then concatenated and form the input for the fourth layer.
Figure 2.
Fusion of features after layer three of a CNN. The features from two streams are passed through max pooling, convolution, batch normalization and ReLU layers. The two outputs are then concatenated and form the input for the fourth layer.
Figure 3.
Fusion of features at different layers of a CNN. (a) Late fusion: Results from two streams are combined at the final layer. (b) Composite fusion: features from two streams are combined at multiple locations of the network
Figure 3.
Fusion of features at different layers of a CNN. (a) Late fusion: Results from two streams are combined at the final layer. (b) Composite fusion: features from two streams are combined at multiple locations of the network
Figure 4.
Training image over the Czech Republic: (a) Sentinel-2 image (R, G, B), (b) Sentinel-1 image (VH) and (c) Ground truth (GT) synthesized from OpenStreetMap; Four classes: farmland (green), forest (olive), water (blue) and urban (yellow). S-1 and S-2 images copyright: “Copernicus Sentinel data [2017]”.
Figure 4.
Training image over the Czech Republic: (a) Sentinel-2 image (R, G, B), (b) Sentinel-1 image (VH) and (c) Ground truth (GT) synthesized from OpenStreetMap; Four classes: farmland (green), forest (olive), water (blue) and urban (yellow). S-1 and S-2 images copyright: “Copernicus Sentinel data [2017]”.
Figure 5.
Potsdam test result: (a) Test image (IR, R, G), (b) corresponding normalized DSM image, (c) Classification result (fusion after layer 3) and (d) Pixels that are misclassified are marked in red. Boundaries in black were ignored during evaluation.
Figure 5.
Potsdam test result: (a) Test image (IR, R, G), (b) corresponding normalized DSM image, (c) Classification result (fusion after layer 3) and (d) Pixels that are misclassified are marked in red. Boundaries in black were ignored during evaluation.
Figure 6.
Vaihingen test result: (a) Test image (IR, R, G), (b) corresponding normalized DSM image, (c) Classification result (fusion after layer 3) and (d) Pixels that are misclassified are marked in red. Boundaries in black were ignored during evaluation.
Figure 6.
Vaihingen test result: (a) Test image (IR, R, G), (b) corresponding normalized DSM image, (c) Classification result (fusion after layer 3) and (d) Pixels that are misclassified are marked in red. Boundaries in black were ignored during evaluation.
Figure 7.
Potsdam and Vaihingen test result: (a) Test image, (b) Fusion after layer 3 result, (c) Composite fusion result and (d) Late fusion result.
Figure 7.
Potsdam and Vaihingen test result: (a) Test image, (b) Fusion after layer 3 result, (c) Composite fusion result and (d) Late fusion result.
Figure 8.
France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap, (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 8.
France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap, (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 9.
Section of France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap, (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 9.
Section of France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap, (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 10.
Section of France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap. Four classes: farmland (green), forest (olive), water (blue), and urban (yellow), (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 10.
Section of France image. (a) Sentinel-2 (R, G, B) image. S-2 image copyright: “Copernicus Sentinel data [2017]”, (b) Ground truth from OpenStreetMap. Four classes: farmland (green), forest (olive), water (blue), and urban (yellow), (c) Result from layer 3 fusion network, (d) Result where GT is available (pixels where GT is not available are masked).
Figure 11.
A Zeebruges test result: (
a) R, G, B image, (
b) DSM, (
c) Layer 3 result, (
d) Late fusion result. Zeebruges (
a,
b) images courtesy grss_dfc_2015 [
12,
13].
Figure 11.
A Zeebruges test result: (
a) R, G, B image, (
b) DSM, (
c) Layer 3 result, (
d) Late fusion result. Zeebruges (
a,
b) images courtesy grss_dfc_2015 [
12,
13].
Table 1.
FCN-32 network is trained on image patches obtained from 14 Potsdam training images. The inference is made on remaining 3 Potsdam images and on 3 Vaihingen training images. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, LnFsn denotes fusion after layer n. The inputs for the fusion networks were (IR, R, G) & (IR, NDVI, nDSM) channels. The top two results for both image sets are shown in bold-underlined and bold fonts.
Table 1.
FCN-32 network is trained on image patches obtained from 14 Potsdam training images. The inference is made on remaining 3 Potsdam images and on 3 Vaihingen training images. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, LnFsn denotes fusion after layer n. The inputs for the fusion networks were (IR, R, G) & (IR, NDVI, nDSM) channels. The top two results for both image sets are shown in bold-underlined and bold fonts.
| | Potsdam Val | Vaihingen Val |
|---|
| Setup | Overall Accuracy | Average F1-Score | Overall Accuracy | Average F1-Score |
|---|
| Pre-trained weights (IR, R, G) | 89.85 | 87.01 | 66.63 | 57.31 |
| Random weights (IR, R, G) | 90.2 | 88.23 | 54.89 | 43.05 |
| CoFsn | 91.51 | 89.5 | 67.95 | 59.39 |
| L1Fsn | 90.43 | 88.28 | 68.86 | 59.02 |
| L2Fsn | 91.23 | 89.20 | 69.11 | 58.57 |
| L3Fsn | 91.36 | 89.27 | 68.89 | 61.91 |
| L4Fsn | 91.03 | 88.88 | 70.65 | 62.91 |
| L5Fsn | 88.42 | 85.52 | 70.39 | 62.09 |
| LaFsn | 90.41 | 87.53 | 72.97 | 63.11 |
Table 2.
Potsdam dataset test results. The fusion networks were tested on (R, G, B) & (IR, NDVI, nDSM) inputs. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. Even though, the DLR_10 method produces an overall accuracy 0.6% higher than L3Fsn (shown in bold font), it consists of two neural networks with a comparatively large number of neurons. The NLPR3 achieves the best result (bold and underlined) because of an additional conditional random fields inference step.
Table 2.
Potsdam dataset test results. The fusion networks were tested on (R, G, B) & (IR, NDVI, nDSM) inputs. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. Even though, the DLR_10 method produces an overall accuracy 0.6% higher than L3Fsn (shown in bold font), it consists of two neural networks with a comparatively large number of neurons. The NLPR3 achieves the best result (bold and underlined) because of an additional conditional random fields inference step.
| F1-Score |
|---|
| Method | Imp. Surface | Building | Low Veg. | Tree | Car | Avg. 5 Classes | Overall Acc. |
|---|
| FCN-8 (R, G, B) [46] | 88.7 | 91.5 | 82.2 | 82.2 | 90.8 | 87.08 | 85.5 |
| L3Fsn (SegNet) | 92.0 | 96.3 | 85.5 | 86.5 | 94.5 | 90.96 | 89.4 |
| L3Fsn (FCN-32) | 92.3 | 96.8 | 86.5 | 87.3 | 91.3 | 90.84 | 90 |
| L3Fsn (FCN-8) | 92.6 | 97.0 | 86.9 | 87.4 | 95.2 | 91.82 | 90.3 |
| LaFsn (FCN-8) | 90.6 | 95.9 | 83.5 | 83.3 | 93.1 | 89.28 | 87.9 |
| CoFsn (FCN-8) | 92.5 | 97.0 | 86.5 | 87.2 | 94.9 | 91.62 | 90.2 |
| DST_5 [45] | 92.5 | 96.4 | 86.7 | 88.0 | 94.7 | 91.66 | 90.3 |
| CASIA2 [11] | 93.3 | 97.0 | 87.7 | 88.4 | 96.2 | 92.52 | 91.1 |
Table 3.
Vaihingen dataset test results. The fusion networks were tested on (IR, R, G) & (IR, NDVI, nDSM) inputs. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3 (with FCN-8 as a base network).
Table 3.
Vaihingen dataset test results. The fusion networks were tested on (IR, R, G) & (IR, NDVI, nDSM) inputs. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3 (with FCN-8 as a base network).
| F1-Score |
|---|
| Method | Imp. Surface | Building | Low Veg. | Tree | Car | Avg. F1-Score | Overall Acc. |
|---|
| LaFsn | 88.8 | 93.5 | 80.5 | 88.5 | 70.2 | 84.3 | 87.7 |
| L3Fsn | 91.2 | 95.3 | 83.1 | 89.2 | 81.3 | 88.02 | 89.7 |
| CoFsn | 91.7 | 95.2 | 83.5 | 89.2 | 82.8 | 88.48 | 89.9 |
| DST_2 [45] | 90.5 | 93.7 | 83.4 | 89.2 | 72.6 | 85.88 | 89.1 |
| DLR_10 [60] | 92.3 | 95.2 | 84.1 | 90.0 | 79.3 | 88.18 | 90.3 |
| Structured RF [9] | 88.1 | 93.0 | 80.5 | 87.2 | 41.9 | 78.14 | 86.3 |
| NLPR3 [11] | 93.0 | 95.6 | 85.6 | 90.3 | 84.5 | 89.8 | 91.2 |
Table 4.
Quantitative Results for Sentinel-1 and -2 images. LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. The L3Fsn method achieves the best results with a kappa value of 0.6161.
Table 4.
Quantitative Results for Sentinel-1 and -2 images. LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. The L3Fsn method achieves the best results with a kappa value of 0.6161.
| | F1-Score | | |
|---|
| Method | Water | Farmland | Forest | Urban | Acc. | kappa |
|---|
| (R, G, B) | 36.18 | 83.01 | 81.96 | 81.25 | 81.32 | 0.5019 |
| (VH, VV, VV/VH) | 51.53 | 85.02 | 84.80 | 81.87 | 84.87 | 0.5965 |
| (B6, B8a, B11) | 63.71 | 81.24 | 74.57 | 67.48 | 76.07 | 0.3618 |
| L3Fsn (R, G, B) & (B6, B8a, B11) | 55.96 | 87.65 | 85.84 | 82.57 | 85.60 | 0.6161 |
| LaFsn (R, G, B) & (B6, B8a, B11) | 66.82 | 86.38 | 85.07 | 82.54 | 85.11 | 0.6029 |
| CoFsn (R, G, B) & (B6, B8a, B11) | 55.26 | 87.92 | 85.63 | 81.69 | 85.37 | 0.6098 |
| FuseNet [37] (R, G, B) & (B6, B8a, B11) | 54.19 | 87.06 | 85.44 | 84.88 | 85.45 | 0.6120 |
Table 5.
Quantitative results for the Zeebruges test images. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. The L3Fsn method achieves the best results with a kappa value of 0.84.
Table 5.
Quantitative results for the Zeebruges test images. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3. The L3Fsn method achieves the best results with a kappa value of 0.84.
| Method | Imp. Srfc | Bldg | Low Veg. | Tree | Car | Cltr | Boat | Water | Over. Acc. | k |
|---|
| L3Fsn | 84.8 | 83.93 | 84.24 | 80.17 | 83.13 | 62.83 | 55.77 | 98.97 | 87.91 | 0.84 |
| LaFsn | 81.67 | 80.20 | 79.99 | 73.64 | 81.86 | 61.47 | 63.71 | 98.59 | 85.22 | 0.81 |
| CoFsn | 81.26 | 76.96 | 74.67 | 77.95 | 82.08 | 57.47 | 50.81 | 98.47 | 83.63 | 0.79 |
| ONERA [55] | 67.66 | 72.7 | 68.38 | 78.77 | 33.92 | 45.6 | 56.1 | 96.5 | 76.56 | 0.7 |
| RGBd AlexNet [13] | 79.10 | 75.60 | 78.00 | 79.50 | 50.80 | 63.40 | 44.80 | 98.20 | 82.32 | 0.78 |
Table 6.
Computational time in ms for the forward and backward pass of the three fusion networks. Time in seconds to generate the result for a test image (France). The test image (France) was divided into 5253 image patches each of size 224 × 224 pixels. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3.
Table 6.
Computational time in ms for the forward and backward pass of the three fusion networks. Time in seconds to generate the result for a test image (France). The test image (France) was divided into 5253 image patches each of size 224 × 224 pixels. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3.
| Method | Time (ms) | Total Time for |
|---|
| | Forward | Backward | A Test Image (s) |
|---|
| L3Fsn | 19.09 | 49.61 | 163 |
| CoFsn | 23.51 | 57.57 | 185 |
| LaFsn | 28.99 | 86.74 | 212 |
Table 7.
GPU memory consumption at inference time and the number of parameters of the three fusion networks. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3.
Table 7.
GPU memory consumption at inference time and the number of parameters of the three fusion networks. In the table, LaFsn denotes late fusion, CoFsn denotes proposed composite fusion, L3Fsn denotes fusion after layer 3.
| Method | GPU Inference | Parameters |
|---|
| | Memory (MB) | (M) |
|---|
| L3Fsn | 1826 | 138.44 |
| CoFsn | 2084 | 137.99 |
| LaFsn | 2880 | 268 |
Table 8.
Two-stage results: overall accuracy of Vaihingen and Zeebruges images. The weights obtained after stage 1 and 2 training were used to generate two corresponding test results.
Table 8.
Two-stage results: overall accuracy of Vaihingen and Zeebruges images. The weights obtained after stage 1 and 2 training were used to generate two corresponding test results.
| | After 1st Stage | After 2nd Stage | After 1st Stage | After 2nd Stage |
|---|
| Method | Overall Accuracy |
|---|
| | Vaihingen | Zeebruges |
| L3Fsn | 89.6 | 89.7 | 87.93 | 87.91 |
| LaFsn | 87.0 | 87.7 | 84.82 | 85.22 |