Using TSX/TDX Pursuit Monostatic SAR Stacks for PS-InSAR Analysis in Urban Areas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Standard PS-InSAR
- Preliminary processing: image import; master selection; co-registration; resampling; reflectivity map generation; amplitude stability index generation;
- Preliminary geocoding: ground control point (GCP) selection; external DEM input; projection of external DEM and synthetic amplitude in SAR coordinates; Mask for PSCs;
- APS estimation: interferometric formation using star graph; select a subset of PSCs according to a certain threshold; triangulation of sparse PSC network and generation of differential phase; deformation and topographic estimation based on given search space; selection of reference point; inversion of initial APS;
- Sparse estimation: interferometric formation using star graph; selection of all PSCs based on a certain threshold; Input of initial APS, differential phase and reference points; deformation and topographic estimations based on the given search space for the PSCs.
2.2. A PS-InSAR Solution for Mono-Static Pursuit Datasets
- Preliminary processing: image import; master selection; co-registration; resampling; reflectivity map generation; amplitude stability index generation;
- Preliminary geocoding: GCP selection; external DEM input; projection of external DEM and synthetic amplitude in SAR coordinates; Mask for PSCs;
- First APS estimation: interferometric formation using only 10 s PM pairs; selection of a subset of PSCs according to a certain threshold; triangulation of sparse PSC network and generation of the differential phase; topographic estimation only based on a given search space; selection of the reference point; inversion of the initial APS;
- First sparse estimation: interferometric formation using only 10 s PM pairs; selection of all PSCs based on a certain threshold; input of initial APS, differential phase, and reference point; topographic estimation only based on the given search space for PSCs;
- Second APS estimation: interferometric formation using a star graph; selection of a subset of PSCs according to a certain threshold; triangulation of sparse PSC networks and generation of a differential phase; deformation estimation based on residual phase components derived in the first round within a given search space; selection of the reference point; inversion of the initial APS;
- Second Sparse estimation: interferometric formation using star graph; selection of all PSCs based on a certain threshold; Input of initial APS, differential phase and reference point; deformation estimation based on the residual phase component derived in first round within a given search space for PSCs;
3. Experiment Results
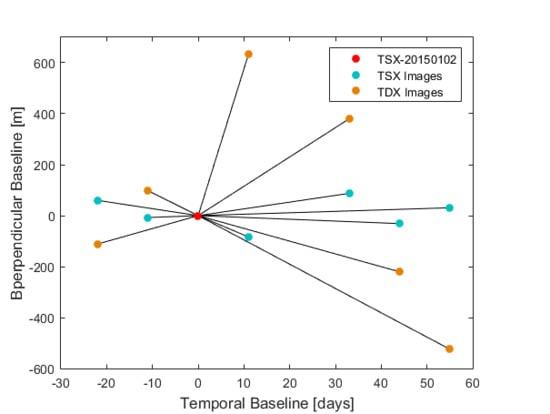
3.1. Study Area and Dataset Information
3.2. Experimental Results
3.2.1. Processing Results from the Standard Method
3.2.2. Processing Results from Our Proposed Method
4. Discussion
4.1. Temporal Coherence
4.2. Topography Estimation
4.2.1. PS Point Numbers
4.2.2. Persistent Scatterer Density
4.3. Deformation Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Lanari, R.; Zeni, G.; Manunta, M.; Guarino, S.; Berardino, P.; Sansosti, E. An integrated SARGIS approach for investigating urban deformation phenomena: A case study of the city of Naples, Italy. Int. J. Remote Sens. 2004, 25, 2855–2862. [Google Scholar] [CrossRef]
- Colesanti, C.; Mouelic, S.L.; Bennani, M.; Raucoules, D.; Carnec, C.; Ferretti, A. Detection of mining related ground instabilities using the Permanent Scatterers technique—A case study in the east of France. Int. J. Remote Sens. 2005, 26, 201–207. [Google Scholar] [CrossRef]
- Vallone, P.; Giammarinaro, M.S.; Crosetto, M.; Agudo, M.; Biescas, E. Ground motion phenomena in Caltanissetta (Italy) investigated by InSAR and geological data integration. Eng. Geol. 2008, 98, 144–155. [Google Scholar] [CrossRef]
- Gernhardt, S.; Adam, N.; Eineder, M.; Bamler, R. Potential of very high resolution SAR for persistent scatterer interferometry in urban areas. Ann. GIS 2010, 16, 103–111. [Google Scholar] [CrossRef]
- Gernhardt, S.; Bamler, R. Deformation monitoring of single buildings using meter-resolution SAR data in PSI. ISPRS J. Photogramm. Remote Sens. 2012, 73, 68–79. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Luzi, G.; Crippa, B. Measuring thermal expansion using X-band persistent scatterer interferometry. ISPRS J. Photogramm. Remote Sens. 2015, 100, 84–91. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Yang, M.; Luo, H.; Liao, M.; Ding, X. Mapping surface deformation and thermal dilation of arch bridges by structure-driven multi-temporal DInSAR analysis. Remote Sens. Environ. 2018, 216, 71–90. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Ding, X.; Liao, M.; Yang, M. Mapping and Characterizing Thermal Dilation of Civil Infrastructures with Multi-Temporal X-Band Synthetic Aperture Radar Interferometry. Remote Sens. 2018, 10, 941. [Google Scholar] [CrossRef]
- Schulze, D.; Zink, M.; Krieger, G.; Böer, J.; Moreira, A. TANDEM-X mission concept and status. In Proceedings of the FRINGE, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Fritz, T.; Rossi, C.; Yague-Martinez, N.; Rodriguez-Gonzalez, F.; Lachaise, M.; Breit, H. Interferometric processing of TanDEM-X data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 2428–2431. [Google Scholar]
- Fritz, T.; Breit, H.; Rossi, C.; Balss, U.; Lachaise, M.; Duque, S. Interferometric processing and products of the TanDEM-X mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1904–1907. [Google Scholar]
- Hajnsek, I.; Krieger, G.; Papathanassiou, K.; Baumgartner, S.; Rodriguez-Cassola, M.; Prats, P. TanDEM-X: First scientific experiments during the commissioning phase. In Proceedings of the 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010; pp. 1–3. [Google Scholar]
- Bachmann, M.; Hofmann, H. Challenges of the TanDEM-X commissioning phase. In Proceedings of the 2010 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010; pp. 1–3. [Google Scholar]
- Prats, P.; Scheiber, R.; Mittermayer, J.; Wollstadt, S.; Baumgartner, S.V.; López-Dekker, P.; Schulze, D.; Steinbrecher, U.; Rodríguez-Cassolà, M.; Reigber, A.; et al. TanDEM-X experiments in pursuit monostatic configuration. In Proceedings of the 2012 9th European Conference on Synthetic Aperture Radar (EUSAR), Nürnberg, Germany, 23–26 April 2012; pp. 159–162. [Google Scholar]
- Lumsdon, P.; Schlund, M.; von Poncet, F.; Janoth, J.; Weihing, D.; Petrat, L. An encounter with pursuit monostatic applications of TanDEM-X mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3187–3190. [Google Scholar]
- Bello, J.L.B.; Martone, M.; Gonzalez, C.; Kraus, T.; Bräutigam, B. First interferometric performance analysis of full polarimetric TanDEM-X acquisitions in the pursuit monostatic phase. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1242–1245. [Google Scholar]
- Bueso-Bello, J.L.; Martone, M.; Prats-Iraola, P.; González-Chamorro, C.; Kraus, T.; Reimann, J.; Jäger, M.; Bräutigam, B.; Rizzoli, P.; Zink, M. Performance Analysis of TanDEM-X Quad-Polarization Products in Pursuit Monostatic Mode. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1853–1869. [Google Scholar] [CrossRef]
- Shi, Y.L.; Wang, Y.Y.; Kang, J.; Lachaise, M.; Zhu, X.X.; Bamler, R. 3D Reconstruction from Very Small TanDEM-X Stacks. In Proceedings of the EUSAR 2018: 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018. [Google Scholar]
- Sjögren, T.; Vu, V. Detection of slow and fast moving targets using hybrid CD-DMTF SAR GMTI mode. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 818–821. [Google Scholar]
- Sjögren, T.; Vu, V.; Mats, P. Experimental result for SAR GMTI using monostatic pursuit mode of TerraSAR-X and TanDEM-X on Staring Spotlight images. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–4. [Google Scholar]
- Ren, Y.; Li, X.M. Derivation of sea surface current fields using TanDEM-X pursuit monostatic mode data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4019–4022. [Google Scholar]
- Velotto, D.; Nunziata, F.; Bentes, C.; Migliaccio, M.; Lehner, S. Investigation of the experimental TanDEM-X pursuit monostatic mode for oil and ship detection. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4023–4026. [Google Scholar]
- Kemp, J.; Burns, J. Agricultural monitoring using pursuit monostatic TanDEM-X coherence in the Western Cape, South Africa. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–4. [Google Scholar]
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Eineder, M.; Younis, M.; De Zan, F.; Prats, P.; Huber, S.; Werner, M.; Fiedler, H.; et al. The tandem-L mission proposal: Monitoring earth’s dynamics with high resolution SAR interferometry. In Proceedings of the Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–6. [Google Scholar]
- Moreira, A. A golden age for spaceborne SAR systems. In Proceedings of the 2014 20th International Conference on Microwaves, Radar, and Wireless Communication (MIKON), Gdansk, Poland, 16–18 June 2014; pp. 1–4. [Google Scholar]
- Huber, S.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A.; Grafmueller, B.; Wolters, R. Tandem-L: Design concepts for a next-generation spaceborne SAR system. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–5. [Google Scholar]
- Wang, Y. Twin-L SAR: Terrain-Wide Swath Interferometric L-Band SAR. In Proceedings of the International Society for Photogrammetry and Remote Sensing (ISPRS) Geospatial Week 2017, Wuhan, China, 18–22 September 2017. [Google Scholar]
- Marple, S.L. Digital spectral analysis: With applications. J. Acoust. Soc. Am. 1998, 86, 2043. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001; Volume 2. [Google Scholar]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry—Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2001, 18, 338–351. [Google Scholar] [CrossRef] [PubMed]
- Perissin, D.; Wang, Z.; Lin, H. Shanghai subway tunnels and highways monitoring through Cosmo-SkyMed Persistent Scatterers. ISPRS J. Photogramm. Remote Sens. 2012, 73, 58–67. [Google Scholar] [CrossRef]



















| Operation Mode | Pursuit Mono-Static | |
|---|---|---|
| Image Mode | Staring Spotlight (ST) | |
| Look Angle | 43.4° | |
| Polarization | VV | |
| Direction | Ascending | |
| Resolution | 0.24 m (azimuth) | |
| 0.80 m (ground range) | ||
| Azimuth Extent | 3 km | |
| Range Extent | 5.5 km | |
| External Information | Acquisition Time | Temperature (°C) |
| 20141211 | 14.5 | |
| 20141222 | 9.1 | |
| 20150102 | 11.6 | |
| 20150113 | 11.2 | |
| 20150204 | 12.4 | |
| 20150215 | 16.7 | |
| 20150226 | 22.0 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Balz, T.; Zhang, L.; Perissin, D.; Liao, M. Using TSX/TDX Pursuit Monostatic SAR Stacks for PS-InSAR Analysis in Urban Areas. Remote Sens. 2019, 11, 26. https://doi.org/10.3390/rs11010026
Wang Z, Balz T, Zhang L, Perissin D, Liao M. Using TSX/TDX Pursuit Monostatic SAR Stacks for PS-InSAR Analysis in Urban Areas. Remote Sensing. 2019; 11(1):26. https://doi.org/10.3390/rs11010026
Chicago/Turabian StyleWang, Ziyun, Timo Balz, Lu Zhang, Daniele Perissin, and Mingsheng Liao. 2019. "Using TSX/TDX Pursuit Monostatic SAR Stacks for PS-InSAR Analysis in Urban Areas" Remote Sensing 11, no. 1: 26. https://doi.org/10.3390/rs11010026
APA StyleWang, Z., Balz, T., Zhang, L., Perissin, D., & Liao, M. (2019). Using TSX/TDX Pursuit Monostatic SAR Stacks for PS-InSAR Analysis in Urban Areas. Remote Sensing, 11(1), 26. https://doi.org/10.3390/rs11010026