Efficient Numerical Full-Polarized Facet-Based Model for EM Scattering from Rough Sea Surface within a Wide Frequency Range
Abstract
:1. Introduction
2. Description of FPFSM
2.1. Near Specular Reflection Direction
2.2. Diffuse Scattering Region
2.3. The Complete Full-Polarized Facet Based Scattering Model
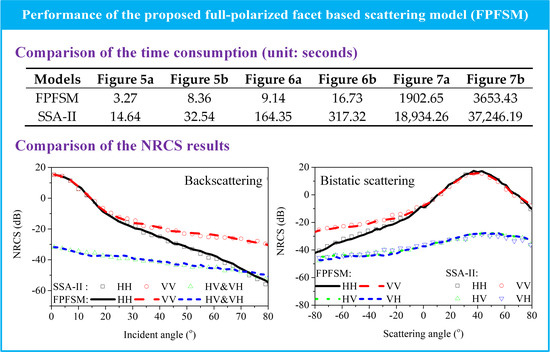
3. Performance of Full-Polarized Facet Based Scattering Model
3.1. Normalized Radar Cross Section Results for Different Wave Bands
3.2. Comparison of Doppler Spectrum
4. Analyses of Electromagnetic Scattering Characteristics at Ka-Band
4.1. Normalized Radar Cross Section under Monostatic Configuration
4.2. Normalized Radar Cross Section under Bistatic Configuration
4.3. Normalized Radar Cross Section Dependence on Wind Speed
4.4. Doppler Spectrum of Time-Evolving Sea Surfaces
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guérin, C.A.; Johnson, J.T. A Simplified Formulation for Rough Surface Cross-Polarized Backscattering Under the Second-Order Small-Slope Approximation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6308–6314. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Perrie, W.; Zhang, B. Cross-Polarization Radar Backscattering from the Ocean Surface and Its Dependence on Wind Velocity. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2188–2192. [Google Scholar] [CrossRef]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Pottier, E. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, H.; Wang, C.; Shan, Z. Similarity analysis of entropy/alpha decomposition between HH/VV dual- and quad-polarization SAR data. Remote Sens. Lett. 2015, 6, 228–237. [Google Scholar] [CrossRef]
- Li, X.F.; Xu, X.J. Scattering and Doppler Spectral Analysis for Two-Dimensional Linear and Nonlinear Sea Surfaces. IEEE Trans. Geosci. Remote Sens. 2010, 49, 603–611. [Google Scholar] [CrossRef]
- Khenchaf, A. Bistatic Scattering and Depolarization by Randomly Rough Surfaces: Application to the Natural Rough Surfaces in X-band. Waves Random Media 2001, 11, 61–89. [Google Scholar] [CrossRef]
- Wang, J.N.; Xu, X.J. Doppler Simulation and Analysis for 2-D Sea Surfaces Up to Ku-Band. IEEE Trans. Geosci. Remote Sens. 2015, 54, 466–478. [Google Scholar] [CrossRef]
- Bass, F.G.; Fuks, I.M.; Kalmyicov, A.I.; Ostrovsky, I.E.; Rosenberg, A.D. Very High Frequency Radiowave Scattering by a Disturbed Sea Surface PART I: Scattering from A Slightly Disturbed Boundary. IEEE Trans. Antennas Propag. 1968, 16, 554–559. [Google Scholar] [CrossRef]
- Voronovich, A.G. Small-slope approximation for electromagnetic wave scattering at a rough interface of two dielectric half-spaces. Waves Random Media 1994, 4, 337–367. [Google Scholar] [CrossRef]
- Li, J.X.; Zhang, M.; Fan, W.N.; Nie, D. Facet-Based Investigation on Microwave Backscattering from Sea Surface with Breaking Waves: Sea Spikes and SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2313–2325. [Google Scholar] [CrossRef]
- Du, Y.; Yang, X.; Chen, K.-S.; Ma, W.; Li, Z. An Improved Spectrum Model for Sea Surface Radar Backscattering at L-Band. Remote Sens. 2017, 9, 776. [Google Scholar] [CrossRef]
- Yang, J.S.; Du, Y.; Shi, J.C. Polarimetric simulations of bistatic scattering from perfectly conducting ocean surfaces with 3 m/s wind speed at L band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1176–1186. [Google Scholar] [CrossRef]
- Reale, F.; Dentale, F.; Carratelli, E.P. Numerical simulation of whitecaps and foam effects on satellite altimeter response. Remote Sens. 2014, 6, 3681–3692. [Google Scholar] [CrossRef]
- Zheng, H.; Khenchaf, A.; Wang, Y.; Ghanmi, H.; Zhang, Y.; Zhao, C. Sea surface monostatic and bistatic EM scattering using SSA-1 and UAVSAR data: Numerical evaluation and comparison using different sea spectra. Remote Sens. 2018, 10, 1084. [Google Scholar] [CrossRef]
- Huang, W.; Liu, X.; Gill, E.W. An empirical mode decomposition method for sea surface wind measurements from X-band nautical radar data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6218–6227. [Google Scholar] [CrossRef]
- Ji, Q.; Shao, W.; Sheng, Y.; Yuan, X.; Sun, J.; Zhou, W.; Zuo, J. A promising method of typhoon wave retrieval from Gaofen-3 synthetic aperture radar image in VV-polarization. Sensors 2018, 18, 2064. [Google Scholar] [CrossRef] [PubMed]
- Clarizia, M.P.; Gommenginger, C.; Di, B.M.; Galdi, C.; Srokosz, M.A. Simulation of L-band bistatic returns from the ocean surface: A facet approach with application to ocean GNSS reflectometry. IEEE Trans. Geosci. Remote Sens. 2012, 50, 960–971. [Google Scholar] [CrossRef]
- Plant, W.J. Microwave Sea Return at Moderate to High Incidence Angles. Waves Random Media 2003, 13, 339–354. [Google Scholar] [CrossRef]
- West, J.C. Correlation of Bragg scattering from the sea surface at different polarizations. Waves Random Media 2005, 15, 395–403. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D. On Ocean SAR Raw Signal Simulation. IEEE Trans. Geosci. Remote Sens. 1993, 31, 880–884. [Google Scholar] [CrossRef]
- Li, J.X.; Zhang, M.; Wei, P.B.; Jiang, W.Q. An Improvement on SSA Method for EM Scattering from Electrically Large Rough Sea Surface. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1144–1148. [Google Scholar] [CrossRef]
- Wei, P.B.; Zhang, M.; Nie, D.; Jiao, Y.C. Improvement of SSA Approach for Numerical Simulation of Sea Surface Scattering at High Microwave Bands. Remote Sens. 2018, 10, 1021. [Google Scholar] [CrossRef]
- Guérin, C.A.; Saillard, M. On the High-Frequency Limit of the Second-Order Small-Slope Approximation. Waves Random Media 2003, 13, 75–88. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves. Waves Random Media 2001, 11, 247–269. [Google Scholar] [CrossRef]
- Gilbert, M.S.; Johnson, J.T. A study of the higher-order small-slope approximation for scattering from a Gaussian rough surface. Waves Random Media 2003, 13, 137–149. [Google Scholar] [CrossRef]
- Klein, L.A.; Swift, C.T. An improved model for the dielectric constant of sea water at microwave frequencies. IEEE Trans. Antennas Propag. 1977, 25, 104–111. [Google Scholar] [CrossRef]
- Voronvich, A.G. A two-scale model from the point of view of the small-slope approximation. Waves Random Media 1996, 66, 73–83. [Google Scholar] [CrossRef]
- Martin, S. An Introduction to Ocean Remote Sensing; Cambridge University Press: New York, NY, USA, 2011; p. 274. ISBN 9781107019386. [Google Scholar]
- Meissner, T.; Wentz, F. An updated analysis of the ocean surface wind direction signal in passive microwave brightness temperatures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1230–1240. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, C.E.; Dentale, F.; Reale, F. Numerical Pseudo-Random Simulation of SAR Sea and Wind Response. In Proceedings of the SEASAR 2006 (ESA SP-613), Frascati, Italy, 23–26 January 2006. [Google Scholar]
- Bass, F.G.; Fuks, I.M. Wave Scattering from Statistically Rough Surfaces; Pergamon: Oxford, UK, 1979; ISBN 9781483187754. [Google Scholar]
- Zhang, M.; Chen, H.; Yin, H.C. Facet-Based Investigation on EM Scattering from Electrically Large Sea Surface with Two-Scale Profiles: Theoretical Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1967–1975. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic waves and oceanic waves: A review. Bound.-Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Wright, J.W. A New Model for Sea Clutter. IEEE Trans. Antennas Propag. 1968, 16, 217–223. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katarsos, K. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floatation buoy. In Ocean Wave Spectra; Prentice Hall: Upper Saddle River, NJ, USA, 1963. [Google Scholar]
- Ye, H.X.; Jin, Y.Q. Parameterization of the tapered incidence wave for numerical simulation of electromagnetic scattering from rough surfaces. IEEE Trans. Antennas Propag. 2005, 53, 1234–1237. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; Haan, S.D. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Oceans 2007, 112, 225–237. [Google Scholar] [CrossRef]
- Hwang, P.A.; Zhang, B.; Toporkov, J.V.; Perrie, W. Comparison of composite Bragg theory and quad-polarization radar backscatter from RADARSAT-2: With applications to wave breaking and high wind retrieval. J. Geophys. Res. 2010, 115, 246–255. [Google Scholar] [CrossRef]
- Hwang, P.A.; Stoffelen, A.; Van Zadelhoff, G.J.; Perrie, W.; Zhang, B.; Li, H.; Shen, H. Cross-polarization geophysical model function for C-band radar backscattering from the ocean surface and wind speed retrieval. J. Geophys. Res. Oceans 2015, 120, 893–909. [Google Scholar] [CrossRef] [Green Version]
- Voronovich, A.G.; Zavorotny, V.U. Depolarization of microwave backscattering from a rough sea surface: Modeling with small-slope approximation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y. Investigation on Doppler shift and bandwidth of backscattered echoes from a composite sea surface. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1071–1081. [Google Scholar] [CrossRef]
- Toporkov, J.V.; Brown, G.S. Numerical simulations of scattering from time-varying, randomly rough surfaces. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1616–1625. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; McGraw-Hill: Boston, MA, USA, 2002; ISBN 9780071226615. [Google Scholar]
- Jiang, W.Q.; Zhang, M.; Wei, P.B.; Nie, D. Spectral Decomposition Modeling Method and Its Application to EM Scattering Calculation of Large Rough Surface with SSA Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1848–1854. [Google Scholar] [CrossRef]
- Andreas, A.B.; Khenchaf, A.; Martin, A. Bistatic Radar Imaging of the Marine Environment Part I: Theoretical Background. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3372–3383. [Google Scholar] [CrossRef]
- Awada, A.; Ayari, M.Y.; Khenchaf, A.; Coatanhay, A. Bistatic scattering from an anisotropic sea surface: Numerical comparison between the first-order SSA and the TSM models. Wave Random Complex Media 2006, 16, 383–394. [Google Scholar] [CrossRef]
















| Models | Figure 5a | Figure 5b | Figure 6a | Figure 6b | Figure 7a | Figure 7b |
|---|---|---|---|---|---|---|
| FPFSM | 3.27 | 8.36 | 9.14 | 16.73 | 1902.65 | 3653.43 |
| SSA-II | 14.64 | 32.54 | 164.35 | 317.32 | 18,934.26 | 37,246.19 |
| Models | Figure 5a | Figure 6a | Figure 7a |
|---|---|---|---|
| FPFSM (Near specular reflection direction) | 23.2 | 58.9 | 4129.3 |
| FPFSM (Diffuse scattering direction) | 2.7 | 3.9 | 167.6 |
| SSA-II | 49.3 | 514.6 | 31,527.8 |
| Models | Figure 5a | Figure 5b | Figure 6a | Figure 6b | Figure 7a | Figure 7b | |
|---|---|---|---|---|---|---|---|
| Mean error | HH | 1.34 | 1.51 | 1.45 | 1.22 | 1.19 | 0.99 |
| VV | 1.10 | 1.49 | 1.12 | 1.02 | 0.84 | 0.92 | |
| HV | 1.20 | 1.23 | 1.26 | 1.45 | 0.71 | 1.93 | |
| VH | 1.20 | 1.19 | 1.26 | 1.72 | 0.71 | 1.54 | |
| Maximum error | HH | 2.88 | 2.81 | 2.73 | 2.45 | 2.53 | 2.71 |
| VV | 2.53 | 2.85 | 2.25 | 1.93 | 2.46 | 2.44 | |
| HV | 2.84 | 2.69 | 2.12 | 2.97 | 2.38 | 2.78 | |
| VH | 2.84 | 2. 87 | 2.12 | 3.06 | 2.38 | 2.89 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, M.; Zhao, Y.; Jiang, W. Efficient Numerical Full-Polarized Facet-Based Model for EM Scattering from Rough Sea Surface within a Wide Frequency Range. Remote Sens. 2019, 11, 75. https://doi.org/10.3390/rs11010075
Li J, Zhang M, Zhao Y, Jiang W. Efficient Numerical Full-Polarized Facet-Based Model for EM Scattering from Rough Sea Surface within a Wide Frequency Range. Remote Sensing. 2019; 11(1):75. https://doi.org/10.3390/rs11010075
Chicago/Turabian StyleLi, Jinxing, Min Zhang, Ye Zhao, and Wangqiang Jiang. 2019. "Efficient Numerical Full-Polarized Facet-Based Model for EM Scattering from Rough Sea Surface within a Wide Frequency Range" Remote Sensing 11, no. 1: 75. https://doi.org/10.3390/rs11010075
APA StyleLi, J., Zhang, M., Zhao, Y., & Jiang, W. (2019). Efficient Numerical Full-Polarized Facet-Based Model for EM Scattering from Rough Sea Surface within a Wide Frequency Range. Remote Sensing, 11(1), 75. https://doi.org/10.3390/rs11010075