A Comparative Study of Texture and Convolutional Neural Network Features for Detecting Collapsed Buildings After Earthquakes Using Pre- and Post-Event Satellite Imagery
Abstract
:1. Introduction
2. Study Area
3. Methodology
3.1. CNNs
3.2. GLCM Texture Features
3.3. Random Forest
3.4. Evaluation Metrics
4. Results
4.1. Performance of CNN-RF
4.2. Performance of Texture-RF
5. Discussion
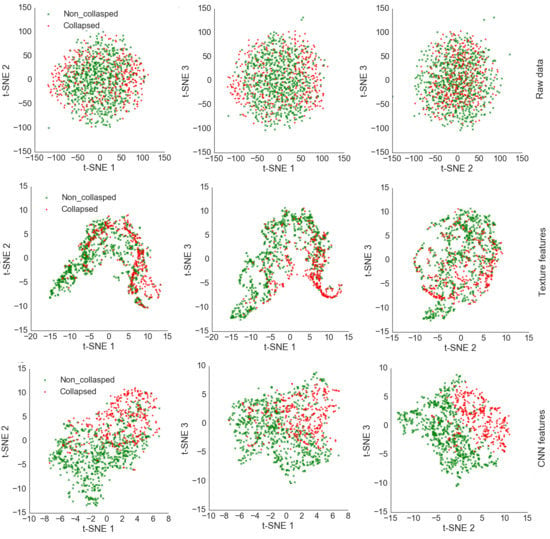
5.1. Feature Visualization
5.2. Relative Importance Variables
5.3. Comparison between CNNs, CNN-RF, and Texture-RF
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moya, L.; Yamazaki, F.; Liu, W.; Yamada, M. Detection of collapsed buildings from lidar data due to the 2016 Kumamoto earthquake in Japan. Nat. Hazards Earth Syst. Sci. 2018, 18, 65. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Sato, M. Urban damage level mapping based on scattering mechanism investigation using fully polarimetric SAR data for the 3.11 east Japan earthquake. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]
- Zhai, W.; Shen, H.; Huang, C.; Pei, W. Building earthquake damage information extraction from a single post-earthquake PolSAR image. Remote Sens. 2016, 8, 171. [Google Scholar] [CrossRef]
- Shafique, M.; van der Meijde, M.; Khan, M.A. A review of the 2005 Kashmir earthquake-induced landslides; from a remote sensing prospective. J. Asian Earth Sci. 2016, 118, 68–80. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Q.; Dou, A.; Wang, X. Extracting damages caused by the 2008 Ms 8.0 Wenchuan earthquake from SAR remote sensing data. J. Asian Earth Sci. 2011, 40, 907–914. [Google Scholar] [CrossRef]
- He, M.; Zhu, Q.; Du, Z.; Hu, H.; Ding, Y.; Chen, M. A 3D shape descriptor based on contour clusters for damaged roof detection using airborne LiDAR point clouds. Remote Sens. 2016, 8, 189. [Google Scholar] [CrossRef]
- Chini, M.; Pierdicca, N.; Emery, W.J. Exploiting SAR and VHR optical images to quantify damage caused by the 2003 bam earthquake. IEEE Trans. Geosci. Remote Sens. 2009, 47, 145–152. [Google Scholar] [CrossRef]
- Blaschke, T.; Strobl, J. What’s wrong with pixels? Some recent developments interfacing remote sensing and GIS. GeoBIT/GIS 2001, 6, 12–17. [Google Scholar]
- Bai, Y.; Adriano, B.; Mas, E.; Gokon, H.; Koshimura, S. Object-based building damage assessment methodology using only post event ALOS-2/PALSAR-2 dual polarimetric SAR intensity images. J. Disaster Res. 2017, 12, 259–271. [Google Scholar] [CrossRef]
- Tu, J.; Sui, H.; Feng, W.; Song, Z. Automatic building damage detection method using high-resolution remote sensing images and 3D gis model. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 43–50. [Google Scholar] [CrossRef]
- Contreras, D.; Blaschke, T.; Tiede, D.; Jilge, M. Monitoring recovery after earthquakes through the integration of remote sensing, GIS, and ground observations: The case of L’Aquila (Italy). Cartogr. Geogr. Inf. Sci. 2016, 43, 115–133. [Google Scholar] [CrossRef]
- Buchroithner, M.; Gevorkian, R.G.; Karachanian, A.S. Resultaty geologo-strukturnogo analisa aerokosmitscheskoj informatsii po sone spitakskogo semletrjasenija (Armenija)—Results of a structural-geological analysis of aero-cosmic data of the Spitak earthquake zone (Armenia). In Proceedings of the 10th Micro Symposium about Relativistic Planetology, Moscow, Russia, 7–11 August 1989; p. 2. [Google Scholar]
- Gamba, P.; Casciati, F. GIS and image understanding for near-real-time earthquake damage assessment. Photogramm. Eng. Remote Sens. 1998, 64, 987–994. [Google Scholar]
- Guirado, E.; Tabik, S.; Alcaraz-Segura, D.; Cabello, J.; Herrera, F. Deep-learning versus OBIA for scattered shrub detection with Google earth imagery: Ziziphus Lotus as case study. Remote Sens. 2017, 9, 1220. [Google Scholar] [CrossRef]
- Janalipour, M.; Mohammadzadeh, A. Building damage detection using object-based image analysis and ANFIS from high-resolution image (case study: BAM earthquake, Iran). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1937–1945. [Google Scholar] [CrossRef]
- Gong, L.; Wang, C.; Wu, F.; Zhang, J.; Zhang, H.; Li, Q. Earthquake-induced building damage detection with post-event sub-meter VHR TerraSAR-X staring spotlight imagery. Remote Sens. 2016, 8, 887. [Google Scholar] [CrossRef]
- Liu, T.; Abd-elrahman, A.; Morton, J.; Wilhelm, V.L.; Liu, T.; Abd-elrahman, A.; Morton, J.; Wilhelm, V.L. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GIScience Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Yu, H.; Cheng, G.; Ge, X. Earthquake-collapsed building extraction from LiDAR and aerophotograph based on OBIA. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; pp. 2034–2037. [Google Scholar]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Pham, T.T.H.; Apparicio, P.; Gomez, C.; Weber, C.; Mathon, D. Towards a rapid automatic detection of building damage using remote sensing for disaster management: The 2010 Haiti earthquake. Disaster Prev. Manag. 2014, 23, 53–66. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 2015 International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 1097–1105. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2014, arXiv:1312.4400. [Google Scholar]
- Hu, F.; Xia, G.; Hu, J.; Zhang, L.; Sensing, R. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Sainath, T.N.; Mohamed, A.R.; Kingsbury, B.; Ramabhadran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8614–8618. [Google Scholar]
- Liu, L.; Ji, M.; Buchroithner, M. Transfer learning for soil spectroscopy based on convolutional neural networks and its application in soil clay content mapping using hyperspectral imagery. Sensors 2018, 18, 3169. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Aziz, O.S. Classification of very high resolution aerial photos using spectral-spatial convolutional neural networks. J. Sens. 2018, 2018, 7195432. [Google Scholar] [CrossRef]
- Ji, M.; Liu, L.; Buchroithner, M. Identifying collapsed buildings using post-earthquake satellite imagery and convolutional neural networks: A case study of the 2010 Haiti earthquake. Remote Sens. 2018, 10, 1689. [Google Scholar] [CrossRef]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Nex, F.; Vosselman, G. Disaster damage detection through synergistic use of deep learning and 3D point cloud features derived from very high resolution oblique aerial images, and multiple-kernel-learning. ISPRS J. Photogramm. Remote Sens. 2018, 140, 45–59. [Google Scholar] [CrossRef]
- Ural, S.; Hussain, E.; Kim, K.; Fu, C.-S.; Shan, J. Building extraction and rubble mapping for city Port-au-Prince post-2010 earthquake with GeoEye-1 imagery and Lidar data. Photogramm. Eng. Remote Sens. 2011, 77, 1011–1023. [Google Scholar] [CrossRef]
- Grünthal, G. European Macroseismic Scale 1998; Cahiers du Centre Europèen de Gèodynamique et de Seismologie, Conseil de l’Europe; Centre Europèen de Géodynamique et de Séismologie: Luxembourg, 1998. [Google Scholar]
- UNITAR/UNOSAT; EC Joint Research Centre; The World Bank. Haiti Earthquake 2010: Remote Sensing Damage Assessment. 2010. Available online: http://www.unitar.org/unosat/haiti-earthquake-2010-remote-sensing-based-building-damage-assessment-data (accessed on 10 May 2017).
- Fang, Z.; Li, W.; Du, Q. Using CNN-based high-level features for remote sensing scene classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time-series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Bialas, J.; Oommen, T.; Rebbapragada, U.; Levin, E. Object-based classification of earthquake damage from high-resolution optical imagery using machine learning. J. Appl. Remote Sens. 2016, 10, 036025. [Google Scholar] [CrossRef]
- Sun, W.; Shi, L.; Yang, J.; Li, P. Building collapse assessment in urban areas using texture information from postevent SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3792–3808. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Zhang, R.; Ma, J.; Lei, L. Collapsed buildings extraction using morphological profiles and texture statistics—A case study in the 5.12 wenchuan earthquake. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Rastiveis, H. Object-oriented analysis of satellite images using artificial neural networks for post-earthquake building change detection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 139–144. [Google Scholar]
- Geiss, C.; Taubenböck, H.; Tyagunov, S. Assessment of seismic building vulnerability from space. Earthq. Spectra 2014, 30, 1553–1583. [Google Scholar] [CrossRef]
- Rastiveis, H.; Eslamizade, F.; Hosseini-Zirdoo, E. Building damage assessment after earthquake using post-event LiDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 595–600. [Google Scholar] [CrossRef]
- Park, J.; Harada, I.; Kwak, Y. A determination of the earthquake disaster area by object-based analysis using a single satellite image. J. Remote Sens. Soc. Jpn. 2018, 38, 14–29. [Google Scholar] [CrossRef]
- Breiman, L.E.O. Randomf forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Dra, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Ma, L.; Fan, S. CURE-SMOTE algorithm and hybrid algorithm for feature selection and parameter optimization based on random forests. BMC Bioinform. 2017, 18, 169. [Google Scholar] [CrossRef]
- Cooner, A.J.; Shao, Y.; Campbell, J.B. Detection of urban damage using remote sensing and machine learning algorithms: Revisiting the 2010 Haiti earthquake. Remote Sens. 2016, 8, 868. [Google Scholar] [CrossRef]
- Mahmoud, A. Plot-Based Land-Cover and Soil-Moisture Mapping Using X-/L-Band SAR Data; Case Study Pirna-South: Saxony, Germany, 2011. [Google Scholar]
- Geiß, C.; Aravena, P.; Marconcini, M.; Sengara, W.; Edwards, M. Estimation of seismic building structural types using multi-sensor remote sensing and machine learning techniques. ISPRS J. Photogramm. Remote Sens. 2015, 104, 175–188. [Google Scholar] [CrossRef]
- Shi, L.; Sun, W.; Yang, J.; Li, P.; Lu, L. Building collapse assessment by the use of postearthquake Chinese VHR airborne SAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2021–2025. [Google Scholar] [CrossRef]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976.
- Pringle, M.J.; Schmidt, M.; Muir, J.S. Geostatistical interpolation of SLC-off Landsat ETM+ images. ISPRS J. Photogramm. Remote Sens. 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Thomlinson, J.R.; Bolstad, P.V.; Cohen, W.B. Coordinating methodologies for scaling landcover classifications from site-specific to global: Steps toward validating global map products. Remote Sens. Environ. 1999, 70, 16–28. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Ou, J.; Liu, X.; Li, X.; Chen, Y. Quantifying the relationship between urban forms and carbon emissions using panel data analysis. Landsc. Ecol. 2013, 28, 1889–1907. [Google Scholar] [CrossRef]
- Tajbakhsh, N.; Shin, J.Y.; Gurudu, S.R.; Hurst, R.T.; Kendall, C.B.; Gotway, M.B.; Liang, J. Convolutional neural networks for medical image analysis: Full training or fine tuning? IEEE Trans. Med. Imaging 2016, 35, 1299–1312. [Google Scholar] [CrossRef]
- Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 2009, 52, 181–184. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan, C.S. A comprehensive survey of deep learning in remote sensing: Theories, tools and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]












| Layer | Shape (N, Width, Length, Bands) | No. of Parameters |
|---|---|---|
| Conv2d_1 | (N, 94, 94, 32) | 896 |
| Activation_1 | (N, 94, 94, 32) | 0 |
| Max_pooling2d_1 | (N, 47, 47, 32) | 0 |
| Conv2d_2 | (N, 45, 45, 64) | 18,496 |
| Activation_2 | (N, 45, 45, 64) | 0 |
| Max_pooling2d_2 | (N, 22, 22, 64) | 0 |
| Conv2d_3 | (N, 20, 20, 64) | 36,928 |
| Activation_3 | (N, 20, 20, 64) | 0 |
| Global_average_pooling2d_1 | (N, 64) | 0 |
| Dense_1 | (N, 32) | 2080 |
| Dropout_1 | (N, 32) | 0 |
| Softmax | (N, 2) | 66 |
| Total | 58,466 |
| Ground Truth | ||||||||
|---|---|---|---|---|---|---|---|---|
| Collapsed Noncollapsed | UA (%) | OA (%) | Kappa (%) | QD (%) | AD (%) | |||
| Predicted | Collapsed | 203 | 37 | 84.6 | ||||
| Noncollapsed | 52 | 424 | 89.1 | |||||
| PA (%) | 79.6 | 91.8 | ||||||
| 87.6 | 72.5 | 2.1 | 10.3 | |||||
| Ground Truth | ||||||||
|---|---|---|---|---|---|---|---|---|
| Collapsed Noncollapsed | UA (%) | OA (%) | Kappa (%) | QD (%) | AD (%) | |||
| Predicted | Collapsed | 165 | 29 | 85.1 | ||||
| Noncollapsed | 90 | 432 | 82.8 | |||||
| PA (%) | 64.7 | 93.7 | ||||||
| 83.4 | 61.7 | 8.5 | 8.1 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, M.; Liu, L.; Du, R.; Buchroithner, M.F. A Comparative Study of Texture and Convolutional Neural Network Features for Detecting Collapsed Buildings After Earthquakes Using Pre- and Post-Event Satellite Imagery. Remote Sens. 2019, 11, 1202. https://doi.org/10.3390/rs11101202
Ji M, Liu L, Du R, Buchroithner MF. A Comparative Study of Texture and Convolutional Neural Network Features for Detecting Collapsed Buildings After Earthquakes Using Pre- and Post-Event Satellite Imagery. Remote Sensing. 2019; 11(10):1202. https://doi.org/10.3390/rs11101202
Chicago/Turabian StyleJi, Min, Lanfa Liu, Runlin Du, and Manfred F. Buchroithner. 2019. "A Comparative Study of Texture and Convolutional Neural Network Features for Detecting Collapsed Buildings After Earthquakes Using Pre- and Post-Event Satellite Imagery" Remote Sensing 11, no. 10: 1202. https://doi.org/10.3390/rs11101202
APA StyleJi, M., Liu, L., Du, R., & Buchroithner, M. F. (2019). A Comparative Study of Texture and Convolutional Neural Network Features for Detecting Collapsed Buildings After Earthquakes Using Pre- and Post-Event Satellite Imagery. Remote Sensing, 11(10), 1202. https://doi.org/10.3390/rs11101202