Convolutional Neural Networks for On-Board Cloud Screening
Abstract
:1. Introduction
2. Methodology
2.1. Network Architecture
2.1.1. Encoder
2.1.2. Decoder
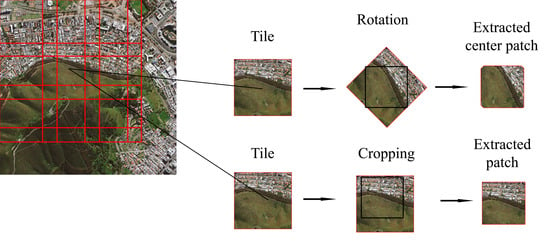
2.2. Generating Training and Test Samples
2.3. Cost Function and Optimization
3. Results
3.1. Dataset
3.2. Test Metrics
- F1-score is defined as the harmonic mean of precision and recall: , where Precision is defined as the ratio of correctly predicted pixels to all predicted pixels regarding a segmentation class: , and Recall is defined as the ratio of correctly predicted pixels to all pixels that belongs to a segmentation class: . Moreover, , and are true positive, false negative and false positive pixels, respectively.
- Overall accuracy is the fraction of correctly labeled pixels for all classes, where and are the number of classes and the number of pixels respectively and denotes true positives for class i.
- mIOU is the ratio of correctly predicted area to the union of predicted pixels and the ground truth which is averaged over all classes.
- Inference memory is the amount of GPU memory, which is occupied by the network during evaluation. The memory consumption is measured based on the maximum allocated GPU memory during inference using a Pytorch implementation of the proposed methodology.
- Computation time considers data loading time, the time interval in which the network processes the extracted patches over a 1000 × 1000 test image, the time needed to stitch patches to form segmentation maps and also the time required to compute the evaluation metrics.
3.3. Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saunders, R.W.; Kriebel, K.T. An improved method for detecting clear sky and cloudy radiances from AVHRR data. Int. J. Remote Sens. 1988, 9, 123–150. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Griggin, M.; Burke, H.h.; Mandl, D.; Miller, J. Cloud cover detection algorithm for EO-1 Hyperion imagery. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium IGARSS’03, Toulouse, France, 21–25 July 2003; Volume 1, pp. 86–89. [Google Scholar]
- Zhang, L.; Huang, X.; Huang, B.; Li, P. A pixel shape index coupled with spectral information for classification of high spatial resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2950–2961. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Pesaresi, M.; Amason, K. Classification and feature extraction for remote sensing images from urban areas based on morphological transformations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1940–1949. [Google Scholar] [CrossRef] [Green Version]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. A multidirectional and multiscale morphological index for automatic building extraction from multispectral GeoEye-1 imagery. Photogramm. Eng. Remote Sens. 2011, 77, 721–732. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. Morphological building/shadow index for building extraction from high-resolution imagery over urban areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 161–172. [Google Scholar] [CrossRef]
- Fisher, A. Cloud and cloud-shadow detection in SPOT5 HRG imagery with automated morphological feature extraction. Remote Sens. 2014, 6, 776–800. [Google Scholar] [CrossRef]
- Merchant, C.; Harris, A.; Maturi, E.; MacCallum, S. Probabilistic physically based cloud screening of satellite infrared imagery for operational sea surface temperature retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.R.; Green, R.O.; Keymeulen, D.; Lundeen, S.K.; Mouradi, Y.; Nunes, D.C.; Castaño, R.; Chien, S.A. Rapid spectral cloud screening onboard aircraft and spacecraft. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6779–6792. [Google Scholar] [CrossRef]
- Shiffman, S. Cloud Detection From Satellite Imagery: A Comparison Of Expert-Generated and Automatically-Generated Decision Trees. 2004. Available online: www.ntrs.nasa.gov (accessed on 1 February 2019).
- Rossi, R.; Basili, R.; Del Frate, F.; Luciani, M.; Mesiano, F. Techniques based on support vector machines for cloud detection on quickbird satellite imagery. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 515–518. [Google Scholar]
- Wagstaff, K.L.; Altinok, A.; Chien, S.A.; Rebbapragada, U.; Schaffer, S.R.; Thompson, D.R.; Tran, D.Q. Cloud Filtering and Novelty Detection using Onboard Machine Learning for the EO-1 Spacecraft. 2017. Available online: https://ai.jpl.nasa.gov (accessed on 1 February 2019).
- Murino, L.; Amato, U.; Carfora, M.F.; Antoniadis, A.; Huang, B.; Menzel, W.P.; Serio, C. Cloud detection of MODIS multispectral images. J. Atmos. Ocean. Technol. 2014, 31, 347–365. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Stateline, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Ghassemi, S.; Fiandrotti, A.; Caimotti, E.; Francini, G.; Magli, E. Vehicle joint make and model recognition with multiscale attention windows. Signal Process. Image Commun. 2019, 72, 69–79. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, Z.; Feng, Y.; Chen, Z. Road extraction from high-resolution remote sensing imagery using deep learning. Remote Sens. 2018, 10, 1461. [Google Scholar] [CrossRef]
- Arief, H.; Strand, G.H.; Tveite, H.; Indahl, U. Land cover segmentation of airborne LiDAR data using stochastic atrous network. Remote Sens. 2018, 10, 973. [Google Scholar] [CrossRef]
- Panboonyuen, T.; Jitkajornwanich, K.; Lawawirojwong, S.; Srestasathiern, P.; Vateekul, P. Semantic segmentation on remotely sensed images using an enhanced global convolutional network with channel attention and domain specific transfer learning. Remote Sens. 2019, 11, 83. [Google Scholar] [CrossRef]
- Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep convolutional capsule network for hyperspectral image spectral and spectral-spatial classification. Remote Sens. 2019, 11, 223. [Google Scholar] [CrossRef]
- Ghassemi, S.; Sandu, C.; Fiandrotti, A.; Tonolo, F.G.; Boccardo, P.; Francini, G.; Magli, E. Satellite image segmentation with deep residual architectures for time-critical applications. In Proceedings of the 26th European Signal Processing Conference, Eternal City, Rome, 3–7 September 2018; pp. 2235–2239. [Google Scholar]
- Ghassemi, S.; Fiandrotti, A.; Francini, G.; Magli, E. Learning and Adapting Robust Features for Satellite Image Segmentation on Heterogeneous Datasets. IEEE Trans. Geosci. Remote Sens. Under review.
- Shi, M.; Xie, F.; Zi, Y.; Yin, J. Cloud detection of remote sensing images by deep learning. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 701–704. [Google Scholar]
- Le Goff, M.; Tourneret, J.Y.; Wendt, H.; Ortner, M.; Spigai, M. Deep learning for cloud detection 2017. Available online: https://hal.archives-ouvertes.fr (accessed on 1 February 2019).
- Wu, X.; Shi, Z. Utilizing multilevel features for cloud detection on satellite imagery. Remote Sens. 2018, 10, 1853. [Google Scholar] [CrossRef]
- Zhaoxiang, Z.; Iwasaki, A.; Guodong, X.; Jianing, S. Small Satellite Cloud Detection Based on Deep Learning and Image Compression. Available online: www.preprints.org (accessed on 1 February 2019 ).
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer–Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switherland, 2015; pp. 234–241. [Google Scholar]
- Mohajerani, S.; Krammer, T.A.; Saeedi, P. A Cloud Detection Algorithm for Remote Sensing Images Using Fully Convolutional Neural Networks. In Proceedings of the 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP), Vancouver, BC, Canada, 29–31 August 2018; pp. 1–5. [Google Scholar]
- Hughes, M.J.; Hayes, D.J. Automated detection of cloud and cloud shadow in single-date Landsat imagery using neural networks and spatial post-processing. Remote Sens. 2014, 6, 4907–4926. [Google Scholar] [CrossRef]
- U.S. Geological Survey, L8 SPARCS Cloud Validation Masks. U.S. Geological Survey Data Release 2016. United States Geological Survey (Reston, Virginia, United States). Available online: www.usgs.gov (accessed on 1 February 2019).
- Francis, A.; Sidiropoulos, P.; Vazquez, E. Real-Time Cloud Detection in High-Resolution Videos: Challenges and Solutions. In Proceedings of the Onboard Payload Data Compression Workshop, Matera, Italy, 20–21 September 2018. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. 2017. Available online: www.pytorch.org (accessed on 1 February 2019).
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Everingham, M.; Eslami, S.A.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 833–851.





| Encoder | Precision | Input Bands | Input Size [Pixels] | Number of Parameters | Inference Memory [MB] | Overall Accuracy [%] | F1-Score [%] | mIOU [%] | |
|---|---|---|---|---|---|---|---|---|---|
| Type | Depth | ||||||||
| Plain | 5 | full | R,B,G,IR | 256 × 256 | 1,269,018 | 15.52 | 95.24 | 90.36 | 83.53 |
| Plain | 5 | full | R | 256 × 256 | 1,266,666 | 14.72 | 94.51 | 87.99 | 80.37 |
| Plain | 5 | full | B | 256 × 256 | 1,266,666 | 14.72 | 94.36 | 88.27 | 80.55 |
| Plain | 5 | full | G | 256 × 256 | 1,266,666 | 14.72 | 94.06 | 87.25 | 79.30 |
| Plain | 5 | full | IR | 256 × 256 | 1,266,666 | 14.72 | 92.38 | 85.15 | 76.08 |
| Plain | 5 | full | All | 256 × 256 | 1,273,722 | 17.11 | 95.15 | 90.22 | 83.49 |
| Plain | 5 | full | R,B,G,IR | 1000 × 1000 | 1,269,018 | 188.60 | 95.18 | 90.01 | 83.43 |
| Plain | 5 | full | R,B,G,IR | 128 × 128 | 1,269,018 | 10.20 | 95.46 | 90.06 | 83.55 |
| Plain | 5 | full | R,B,G,IR | 64 × 64 | 1,269,018 | 9.20 | 95.27 | 89.16 | 82.39 |
| Plain | 5 | half | R,B,G,IR | 256 × 256 | 1,269,018 | 8.05 | 85.06 | 75.45 | 55.49 |
| Plain * | 5 | full | R,B,G,IR | 256 × 256 | 318,478 | 7.03 | 95.28 | 90.08 | 83.09 |
| Plain | 5 | full | R,B,G,IR | 256 × 256 | 80,232 | 3.87 | 94.79 | 88.90 | 81.37 |
| Plain ** | 5 | full | R,B,G,IR | 256 × 256 | 1,264,946 | 11.83 | 95.05 | 89.40 | 82.39 |
| ResNet | 18 | full | R,B,G,IR | 256 × 256 | 16,550,722 | 132.56 | 96.24 | 92.59 | 86.85 |
| ResNet | 34 | full | R,B,G,IR | 256 × 256 | 26,658,882 | 267.23 | 96.42 | 92.39 | 86.45 |
| ResNet | 50 | full | R,B,G,IR | 256 × 256 | 103,629,954 | 889.29 | 96.23 | 91.77 | 85.62 |
| U-net | 9 | full | R,B,G,IR | 256 × 256 | 39,402,946 | 315.36 | 96.08 | 91.01 | 84.89 |
| FMask | - | full | All | 1000 × 1000 | - | - | 86.81 | 70.11 | 62.01 |
| Deeplab V3+ | |||||||||
| ResNet | 101 | full | R,B,G,IR | 256 × 256 | 59,342,562 | 503.7 | 94.87 | 89.47 | 82.07 |
| Xception | - | full | R,B,G,IR | 256 × 256 | 54,700,722 | 481.69 | 89.85 | 83.58 | 73.51 |
| Encoder | Precision | Input Bands | Input Size [Pixels] | Data Loading [ms] | Inference [ms] | Stitch [ms] | Eval Metrics [ms] | Total [ms] | |
|---|---|---|---|---|---|---|---|---|---|
| Type | Depth | ||||||||
| Plain | 5 | full | 4 | 256 × 256 | 37 | 168 | 110 | 415 | 730 |
| Plain | 5 | full | 1 | 256 × 256 | 8 | 167 | 110 | 415 | 700 |
| Plain | 5 | full | 10 | 256 × 256 | 7240 | 170 | 110 | 415 | 7935 |
| Plain | 5 | full | 4 | 1000 × 1000 | 17 | 171 | 0 | 415 | 603 |
| Plain | 5 | full | 4 | 128 × 128 | 45 | 146 | 110 | 415 | 716 |
| Plain | 5 | full | 4 | 64 × 64 | 80 | 1136 | 110 | 415 | 1741 |
| Plain | 5 | half | 4 | 256 × 256 | 18 | 158 | 110 | 415 | 701 |
| Plain * | 5 | full | 4 | 256 × 256 | 37 | 153 | 110 | 415 | 715 |
| Plain | 5 | full | 4 | 256 × 256 | 37 | 100 | 110 | 415 | 662 |
| Plain ** | 5 | full | 4 | 256 × 256 | 37 | 150 | 110 | 415 | 712 |
| ResNet | 18 | full | 4 | 256 × 256 | 37 | 407 | 110 | 415 | 969 |
| ResNet | 34 | full | 4 | 256 × 256 | 37 | 536 | 110 | 415 | 1098 |
| ResNet | 50 | full | 4 | 256 × 256 | 37 | 733 | 110 | 415 | 1295 |
| U-net [32] | 9 | full | 4 | 256 × 256 | 37 | 720 | 110 | 415 | 1282 |
| FMask [39] | - | full | 10 | 1000 × 1000 | 37 | 1470 | - | 415 | 1922 |
| Deeplab V3+ | |||||||||
| ResNet | 101 | full | 4 | 256 × 256 | 37 | 422 | 110 | 415 | 984 |
| Xception | - | full | 4 | 256 × 256 | 37 | 441 | 110 | 415 | 1003 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghassemi, S.; Magli, E. Convolutional Neural Networks for On-Board Cloud Screening. Remote Sens. 2019, 11, 1417. https://doi.org/10.3390/rs11121417
Ghassemi S, Magli E. Convolutional Neural Networks for On-Board Cloud Screening. Remote Sensing. 2019; 11(12):1417. https://doi.org/10.3390/rs11121417
Chicago/Turabian StyleGhassemi, Sina, and Enrico Magli. 2019. "Convolutional Neural Networks for On-Board Cloud Screening" Remote Sensing 11, no. 12: 1417. https://doi.org/10.3390/rs11121417
APA StyleGhassemi, S., & Magli, E. (2019). Convolutional Neural Networks for On-Board Cloud Screening. Remote Sensing, 11(12), 1417. https://doi.org/10.3390/rs11121417