GNSS-R Soil Moisture Retrieval Based on a XGboost Machine Learning Aided Method: Performance and Validation

Abstract

Global navigation satellite system (GNSS)-reflectometry is a type of remote sensing technology and can be applied to soil moisture retrieval. Until now, various GNSS-R soil moisture retrieval methods have been reported. However, there still exist some problems due to the complexity of modeling and retrieval process, as well as the extreme uncertainty of the experimental environment and equipment. To investigate the behavior of bistatic GNSS-R soil moisture retrieval process, two ground-truth measurements with different soil conditions were carried out and the performance of the input variables was analyzed from the mathematical statistical aspect. Moreover, the feature of XGBoost method was utilized as well. As a recently developed ensemble machine learning method, the XGBoost method just emerged for the classification of remote sensing and geographic data, to investigate the characterization of the input variables in the GNSS-R soil moisture retrieval. It showed a good correlation with the statistical analysis of ground-truth measurements. The variable contributions for the input data can also be seen and evaluated. The study of the paper provides some experimental insights into the behavior of the GNSS-R soil moisture retrieval. It is worthwhile before establishing models and can also help with understanding the underlying GNSS-R phenomena and interpreting data.

1. Introduction

The global navigation satellite system (GNSS), including the US GPS, Europe Union GALILEO, Russia GLONASS, and China BeiDou system has achieved great success with an unprecedented impact on all positioning-related areas. It can not only provide spatial information for global users with navigation, positioning information, speed measurement, timing, but also have the opportunity of L-band microwave signals with high time-resolution. As further development of GNSS, the target’s reflected signal can be received and utilized [1,2,3]. Then the way of utilizing the GNSS reflected signals were employed to detect the targets. This is a new concept of remote sensing called GNSS-reflectometry (GNSS-R), featured with no special radar transmitter. Besides, it is a low-cost option with wide global coverage, a large amount of data acquisition, and can also be a powerful complement to other traditional remote sensing methods.

GNSS-R can be regarded as a bi-static radar concept system. In the past 20 years, theoretical [4] and experimental [5] studies using GNSS-R have demonstrated the potential of GNSS-R in remote sensing measurements. There are mainly two types of GNSS-R applications: Altimetry and scatterometry. This GNSS-R technique was firstly proposed for ocean altimetry [5], which is one of the main applications. The altimetry makes use of propagation delay of the reflected signals (from waveform or carrier phase) to measure the surface elevation [6,7]. Another main GNSS-R application is scatterometry that was proposed by Hall and Cordey [4], which used the power/shape information of the waveform (or DDM) to characterize the surface roughness or reflectivity for wind speed retrieval [8,9,10,11], soil moisture measurement [12,13], or sea ice detection [10,14]. In addition, with the continuous development of GNSS-R remote sensing technology, it has been widely used in many fields such as measuring the snow depth [15], tsunami [16], vegetation biomass [17], flooding inundation [18], and inland water [19,20]. The experimental platform has also evolved from ground-based experiments [21] to aircraft [12], balloons [22], and the latest low-orbit satellite [23] platform for measuring hurricanes.

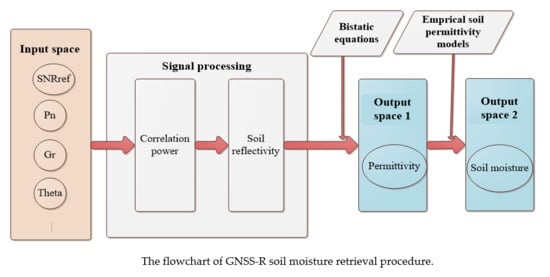
In 2002, NASA took the lead in launching a series of soil moisture remote sensing flight experiments (SMEX02-03) using GPS reflection signals. The entire system effectively measured the signal power that varies with the soil moisture content [12]. Based on the bistatic radar configuration, two antennas were used respectively to receive the direct signal from the satellite and signals reflected from the ground. A right-hand circularly polarized antenna (RHCP) was oriented toward the sky, and a left-hand circularly polarized (LHCP) antenna (single-polarized) or added a right-hand circularly polarized antenna (constituting dual-polarization) perpendicular to the ground [21]. The dielectric constant was solved by using the soil reflectivity and the bistatic radar equation. Then, the soil water content can be obtained by various permittivity inversion models (permittivity–soil moisture). As an extension of the earlier work, a calibration process was added to the subsequent soil moisture remote sensing experiment, and a new reflectometer was used to record the data from the satellite with a high elevation angle (greater than 65°) in the visible range. The results showed that the received calibrated soil reflectivity could be detected and used to estimate the expected relationship between the dielectric constant and soil moisture [24].

After that, researchers proposed another interference pattern technique (IPT) to retrieve the soil moisture content [25]. A left-hand circularly polarized antenna or a vertically polarized antenna, which oriented towards the horizontal, was used to receive the interference signals from dual paths of direct and reflected. The ground receiver SMIGOL reflectometer was used to measure the instantaneous power that is from the interference of the direct and the reflected signal from the ground. Then, the soil moisture was determined by the position of the point (the notch point) where the amplitude fluctuation of the instantaneous power is the smallest.

Another similar approach used GPS multipath reflection signals to perform soil content retrieval and is presented with only one antenna and a classical GNSS receiver [26,27,28]. A representative result [29] is from the University of Colorado, USA. The experiment used a right-hand circularly polarized antenna pointing to the sky and a GPS receiver featured with a geodetic characteristic to receive the direct signals and land-surface reflected signals that caused multipath effects. By measuring the signal-to-noise ratio of the received signal, soil moisture content can be obtained, and the method can be applied to sensing other different objects, such as inverted barometer and storm [30].

At present, various types of space-based, on-board observation experiments are vigorously carried out, and many countries are vigorously promoting related applications [31]. Following the launch of the UK-DMC satellite carrying GPS reflected signal receiving equipment in the UK in 2003 [32], the international exploration of GNSS-R spaceborne observations has developed rapidly. For example, the UK TDS-1 satellite launched in Kazakhstan in 2014 is equipped with SGR-ReSI (Space GNSS Receiver–Remote Sensing Instrument) sensors for GNSS-R measurements [33] are currently used for soil moisture inversion studies [34]. NASA has launched the CYGNSS observation constellation in December 2016.

Especially, some significant results have been found utilizing space-borne data for the soil moisture content (SMC) application. For instance, the sensitivity of GNSS-R observables and SM was studied well in detail using TDS-1 data [35]. The sensitivity of the calibrated GNSS-R reflectivity to surface soil moisture was found to be ~0.09 dB/% at an incident angle of ~30° and decrease as the angle of incidence increased. In another study concerning the first global-scale assessment of GNSS-R, soil moisture active passive (SMAP) mission for soil moisture and biomass determination and scattering properties over land were evaluated and the results showed that the sensitivity to the effects of the Earth’s topography and above ground biomass (ABG) was even over that of Amazonian and Boreal forests [36]. For the CYGNSS mission, the influence of the GNSS satellites’ elevation angle on the reflectivity of LHCP, as a function of soil moisture content (SMC) and effective surface roughness parameter was revealed [37]. Also, the relationship between forward scattered L-band global navigation satellite system (GNSS) signals, recorded by the CYGNSS constellation and SMAP soil moisture (SM) was studied [38]. It showed the sensitivity of CYGNSS to SM that varies spatially and can be used to convert reflectivity to the estimates of SM. The unbiased root-mean-square difference between daily average CYGNSS-derived SM and SMAP SM is 0.045 cm³/cm³ and is similarly low between CYGNSS and in situ SM. The development of space-borne sensors was greatly promoting the related study on a global scale.

In the meanwhile, many empirical and electromagnetic bistatic models were evolved [39,40,41], enriching the knowledge of the scattering effects taking place in GNSS-R soil moisture retrieval. It is crucial to choose features that have the greatest impact on the results so as to reduce the number of variables when building a model, which is occasionally overlooked. Apart from that, most of the researches only focus on the studies of the soil moisture retrieval algorithm. Besides, the existing methods of soil moisture retrieval using GNSS-R technology are mostly based on analytical and semi-empirical models, which often need plenty of experimental data and are deficient in generalization ability. Moreover, the complex modeling process and uncertainty of the experimental environment (such as the inconsistency of the direct and the reflected receiving channel, the noise of the signal receiver, and so on) have a direct influence on the accuracy of the soil moisture estimation. Therefore, there is an urgent need to evaluate the contribution and sensitivity of the input variables, which could be quite significant in doing experiments and interpreting behavior.

The soil moisture retrieval using GNSS-R can be regarded as a nonlinear regression problem and received data can be taken as many input features (variables). Besides the traditional methods, the latest XGBoost based on the Boosting algorithm [42], which is good at variable importance estimation was introduced here to evaluate the variable contribution in GNSS-R.

The Boosting algorithm is a popular and effective integrated learning algorithm in the field of data mining. By weighting and superimposing each weak classifier to form a strong classifier, the prediction error is effectively reduced and the classification results with higher accuracy are obtained. Based on the boosting algorithm, an algorithm called Gradient Boosting was proposed to continuously reduce the residuals and further reduce the residuals of the previous model in the gradient direction to obtain a new model. After that, an improved Gradient Boosting algorithm, Extreme Gradient Boosting (XGBoost) was proposed in 2015 [42].

In recent years, XGBoost has been widely used in-store sales forecasting, hazard risk prediction, power load forecasting, and other fields [43,44,45]. The most important reason for its success is that it is scalable in all scenarios. The scalability of XGBoost is determined by the optimization of several important models and algorithms, including a new tree learning algorithm for processing sparse data and a reasonable weighted quantile sketch process. The weight of the instance is allowed to be processed in the learning of the approximate tree. At the same time, parallel and distributed computing can continuously improve the learning rate of the tree, thus exploring a faster model. More importantly, XGBoost utilizes non-core computing, enabling the user to process hundreds of millions of samples.

Different from the traditional decision tree algorithm, XGBoost adds regular terms such as leaf node weight and tree depth to the cost function. On one hand, it can control the complexity of the model; on the other hand, it can prevent over-fitting phenomenon [46]. At the same time, it uses a second-order Taylor expansion approximation to the cost function, which makes the approximation of the objective function closer to the actual value, thus improving the prediction accuracy. In recent years, the XGBoost algorithm has achieved excellent results due to its high operational efficiency and prediction accuracy in the field of machine learning and data mining [47].

In this paper, XGBoost learning method is aided to understand the behavior and the contribution of the input variables of GNSS-R. By utilizing the XGBoost algorithm to evaluate the contribution of the input variables (such as SNR, receiver noise…), the sensitivity of the input variables to the retrieval results is shown. In addition, the results of ground-truth measurements (corresponding to two typical soil types and different soil conditions) are used to confirm the analysis performed with XGBoost learning method and investigate the performance of GNSS-R retrieval. The variation rate of the retrieved results with respect to input variables is analyzed. This knowledge can help the soil moisture retrieval and modeling process. The paper is organized as follows: In Section 2, the GNSS-R soil moisture retrieval and XGBoost algorithm are presented. Section 3 is focused on the results performed by XGBoost and shows the statistical data analysis obtained from ground-truth experiments. Finally, discussions of the results and conclusions are drawn in Section 4.

2. Theory and Methods

2.1. The Bistatic GNSS-R Soil Moisture Retrieval Method

The GPS satellite, ground surface, and receiver constitute a bistatic radar system as described in Figure 1. The right-handed circularly polarized antenna receives the direct signal and the left-handed circularly polarized antenna receives the reflected signal. The soil reflectivity is obtained by measuring the power of the reflected GPS signal. In the meanwhile, the surface roughness causes scattering from a glistening zone that contributes to non-coherent power around the specular reflection point. As the roughness increases, the scattering occurs and the incoherent component of the reflected signal increases. For perfect flat surfaces, Fresnel reflection is satisfied and the received power are coherent. As we assumed a smooth surface in this study, the power we received is predominated with LHCP coherent component. Then the soil moisture retrieval method using reflected signal power is based on the inversion of the bistatic radar equation:

$$P_{lr}^c=\frac{P_t{G}_t}{4\pi {(R_{st}+R_{rs})}^2}\frac{G_{\mathrm{r}}{\lambda }^2}{4\pi }{\mathsf{\Gamma }}_{lr}$$

(1)

where subscript $lr$ represents the scattering when the satellite incident signal is right-hand polarized and inverts the polarization to LH after surface reflection, $P_t$ is the power of the transmitted signal, $G^t$ is the transmitter antenna gain, $G^r$ is the gain of the receiver antenna, and $\lambda$ is the wavelength (19.042 cm for GPS L1 signal). $R_{rs}$ and $R_{st}$ is the distance between the receiver, the specular point, and the satellite respectively. ${\mathsf{\Gamma }}_{lr}$ is the power reflectivity of the reflecting surface.

The term ${\mathsf{\Gamma }}_{lr}$ in Equation (1) (smooth surface) decreases due to increasing roughness, which can be written as [48]:

$${\mathsf{\Gamma }}_{lr}(\theta )={\left|R_{lr}\left(\theta \right)\right|}^2\chi \left(z\right)$$

(2)

where $R_{lr}$ is the Fresnel reflection coefficient, $\chi (z)$ is the probability density function of the surface height. In the condition of the flat surface $\chi \left(z\right)=1$, the reflectivity ${\mathsf{\Gamma }}_{lr}$ becomes the amplitude squared of the Fresnel reflection coefficient $R_{lr}$.

Combining (1) and (2), the processed SNR of peak power can be written as:

$$SN{R}_{peak}^{refl}=\frac{P_{lr}^c{G}_p}{P_n}=\frac{P_r^t{G}^t{G}^r{\lambda }^2{G}_p}{{\left(4\pi \right)}^2{\left(R_{st}+R_{rs}\right)}^2{P}_n}{|R_{lr}|}^2$$

(3)

where $P_n$ is the noise power and $G_P$ is the processing gain due to the de-spread of the GPS C/A code.

The Fresnel reflection coefficient $R_{lr}$ can be expressed as linear polarization modes [49]:

$$R_{lr}=R_{rl=}\frac{1}{2}\left(R_{vv}-R_{hh}\right)$$

(4)

where $R_{hh}$ and $R_{vv}$ are the Fresnel coefficients for horizontal and vertical polarization [50]:

$$R_{hh}(\theta )=\frac{\cos \theta -\sqrt{{\epsilon }_r-{\sin }^2\theta }}{\cos \theta +\sqrt{{\epsilon }_r-{\sin }^2\theta }}$$

(5)

$$R_{vv}(\theta )=\frac{{\epsilon }_r\cos \theta -\sqrt{{\epsilon }_r-{\sin }^2\theta }}{{\epsilon }_r\cos \theta +\sqrt{{\epsilon }_r-{\sin }^2\theta }}$$

(6)

where $\theta$ is the incident angle, in which ${\epsilon }_r$ is the dielectric constant of the surface, ${\epsilon }_r=\epsilon /{\epsilon }_0-j60\lambda \sigma$. ${\epsilon }_0$ is the free-space permittivity, $\sigma$ is the electric conductivity, and $\lambda$ is the wavelength. In the case of dry terrain or almost dry, the imaginary part of the permittivity can be neglected [51,52]. With this hypothesis, the real part of the permittivity can be obtained from Equations (3)–(6), when the reflected signals are received [51]. Here the input variables are $SN{R}_{refle}^{peak}$, $P_n$, $G_r$, $\theta$ respectively as shown in Figure 2.

In Figure 2, the soil reflectivity is obtained by calculating the correlation power of both the reflected signal and the direct signal. In this study, a coherent integration (1 ms) was determined by the length of the GPS PRN (pseudorandom noise) code sequence. Generally, due to the attenuation of signal power caused by surface reflection and the presence of fading noise introduced by surface scattering, 1 ms of integration is not enough to get the correlation peak, consecutive 1 ms coherent correlations must be averaged. This process is known as non-coherent integration. There is not a defined rule governing the choice but it should only be determined by the specific application and by its own situation. In this study, 500 ms of non-coherent integration time is used since it is examined to be long enough to eliminate the effects of speckle noise and short enough to have a good resolution of the surface by multiple experiments. After that, the reflectivity is used to obtain the permittivity through the bistatic radar equations [53]. We must note that the permittivity is strongly related to the soil moisture content. The relationship between soil permittivity and soil moisture is given by the soil permittivity models. Due to its complex structure, simplified empirical or semi-empirical models are used as a function of permittivity in practical applications [54,55,56].

The performance of GNSS-R soil moisture retrieval is an important issue, which is determined by many factors: (1) The geometric and physical characteristics of the reflected surface, such as the statistical distribution of the ground height, the composition of the soil, etc., which impact the received SNR. (2) Parameters of the GNSS-R system, such as the behavior of the transmitting and receiving antennas ($G_r$, $P_n$), and the elevation angle ($\theta$), etc. Except for the above-concerned parameters (input variables), some random factors, the appearance of the surface roughness, vegetation, e.g., leaf orientation, height of the vegetation, etc., may influence the signal collection in the real case. Due to the complex interaction of these parameters, the retrieval of soil moisture content using GNSS-R is commonly based on semi-empirical models. The random factors can be regarded as system noise and suppressed by machine learning methods. Here we considered the retrieval procedure as a nonlinear regression problem with the input variables ($SNR$, $P_n$…) and output variables (permittivity, soil moisture) based on the early work [46] as shown in Figure 2.

2.2. XGboost

XGBoost is an improved algorithm based on the gradient-enhanced decision tree, which can effectively construct enhanced trees and run parallel computing. Compared with the traditional GBDT (gradient boosting decision tree) algorithm that only uses the first-order derivative information, the XGBoost performs the second-order Taylor expansion on the loss function and provides higher efficiency of solving the optimal solution [44].

The flowchart of the XGBoost algorithm [42] is summarized in Figure 3.

Advantages of XGBoost [44]:

(1)

Using the second-order Taylor expression to approximate the objective function, making it easier to find the optimal solution;

(2)

It can handle sparse and missing data;

(3)

Generating a decision tree using the structural score;

(4)

The split node uses the candidate set so that the algorithm runs fast;

(5)

Define the complexity of the tree and apply it to the objective function to grasp the complexity of the model;

(6)

Over-fitting can be prevented by samplings of column features.

The XGBoost also has some disadvantages: The complexity is slightly higher for using XGB to do the feature importance sorting because XGB uses level-wise to generate decision trees. It splits the leaves of the same layer at the same time, thus performing multi-thread optimization, which can avoid overfitting. The traversal selects the optimal segmentation point. When the amount of data is large, the method is time-consuming [57,58].

2.3. XGboost for the Variable Importance Assessment

The feature selection of XGBoost is based on the initial feature set to establish the classification model, to examine the performance of the feature in the model, and to obtain the importance of the feature. According to the degree of variable importance to search and evaluate the feature subset, an optimal subset will be generated. It is a kind of embedded and filtered feature selection method [57].

The core of the algorithm is to optimize the value of the objective function. The gradient enhancement construct is enhanced by the tree to intelligently acquire feature scores, indicating the importance of each feature to the training model. In an enhancement tree, the more times a feature is used to make a critical decision, the higher its score. The algorithm calculates the importance by “gain”, “frequency”, and “coverage”. Gain is the primary reference factor that determines the importance of a branch feature. Frequency is the simplification of gain, as measured by the number of occurrences of a feature in all construction trees. Coverage is the relative value of feature observations. In this study, the feature quantity was determined by the “gain” [47].

When doing the feature selection using the XGBoost algorithm, feature importance calculation is integrated into the classification process. A new tree is created in each iteration of the round, and the branch node of the tree is a feature variable. Feature importance is based on a feature can be selected as the split node of the tree. Each time a feature is added to the tree as a split node, all possible split points are enumerated using the greedy method, from which the best split point is selected [58].

The best split point corresponds to the maximum gain, and the gain $G_{ain}$ is calculated [47]. Good features and splitting points can improve the squared difference on a single tree. The more improvements, the better the splitting point, the more important this feature is. When all the trees are established, the calculated node importance is averaged in the forest. The more times a feature is selected as a split point, the higher the importance.

For a tree $T$ with $J$ branch nodes, if $J$ is selected as the split variable on this tree, the sum of the mean squared errors on all branch nodes $t$ is calculated, e.g., the importance of feature $j$ on this tree is [42]:

$${\widehat{I}}_j^2\left(T\right)={\displaystyle \sum _{t=1}^{J-1}{\widehat{I}}_j^{2}P\left(v_t=j\right)}$$

(7)

where ${\widehat{I}}_j^2$ is the improvement of squared error of a node $t$. Set ${\overline{y}}_l$ and ${\overline{y}}_r$ with the predicted mean values of the left and right subtrees respectively, and $w_l$ and $w_r$ are the weights of the nodes of the left and right subtrees respectively [42].

$$I^2\left(R_l,R_r\right)=\frac{w_l{w}_r}{w_l+w_r}{\left(\overline{y_l}+\overline{y_r}\right)}^2$$

(8)

By summing the importance of the features $t$ on each tree and making an average, the final importance can be obtained for forests with $M$ trees [42]:

$$I_t^2=\frac{1}{M}{\displaystyle \sum _{m=1}^M{I}_t^2\left(T_m\right)}$$

(9)

3. Results and Analysis

In this section, we show the GNSS-R soil moisture retrieval performance analysis from two different points of view. The first one is to utilize the XGBoost algorithm to analyze the importance of the input variables. The input variables in GNSS-R are taken as different input features in XGBoost algorithm. The simulated data set are shown considering the GNSS-R bistatic soil moisture retrieval equations in the case of flat surface. Then, the variable importance of the input variables is shown and analyzed by means of three different parameter issues. To investigate the contribution of the different input variables to permittivity and soil conditions (including two typical soil types) respectively. For the second part, it focuses on ground-truth measurements. Two different soil compositions and moisture terrain were chosen to do GNSS-R experiments. Some input variables are analyzed mathematically to validate the results obtained by XGBoost, and the performance of GNSS-R soil moisture retrieval is analyzed in details.

3.1. GNSS-R Soil Moisture Retrieval Data Set

The data set was simulated and trained to analyze the performance of the input variables of GNSS-R by using XGBoost. We considered the soil moisture content and the permittivity had a positive correlation, and some established soil permittivity models [54,55] could be used to retrieve the soil moisture from permittivity, so the permittivity is the output variable that we obtained firstly using the bistatic radar equations for observation, under the assumption of a flat surface [53].

The simulated training set mainly consists of the following input vectors:

• $\theta$, Elevation data (from 35 degrees to 85 degrees);
• $G_r$, Receiver Gain (from 2.5 to 3.5 dB);
• $SNRrh$, the signal to noise ratio from the reflected channel (from 2 to 26 dB);
• $P_n$, the total noise power of the receiver (from −130 to −150 dB).

The range of the input vector was set with the idea of staying as close as possible to the experimental situation. Those variables ($\theta$, $G_r$, $P_n$, and $SNRrh$) were the observables for the variable importance analysis. Other input vectors, such as $R_r$ (distance from the transmitter to a specular point), $P_t$ (transmitted power from GPS satellite), $G_t$ (transmitter antenna gain), and $G_{pr}$ (signal processing gain) were constant numbers that depend on the GNSS-R system and were not shown here.

With the GNSS-R retrieval procedure as shown in Figure 2, the simulated data were obtained and shown in order to understand the relationship between the SNR, elevation angle, and the permittivity in Figure 4. The dataset of Figure 4 contained 1000 samples. With the increment of the elevation angle and SNR, the permittivity was also increased as shown in Figure 4.

Figure 5a shows the relationship between the SNR and the permittivity when the elevation angle was a constant number (e.g., 84°). Figure 5b considers the relationship between the elevation angle and the permittivity when the SNR was a constant value (20 dB). It is noted that the obtained permittivity was computed from the formulas that comprise the variables SNR and elevation angle [53]. In Figure 5, it was possible to observe a significant result that the permittivity increased with the increment of the SNR when the elevation angle was a constant value. On the other hand, the permittivity was quite constant for elevation angle ranging between 50° to 85° when we fixed the value of the received SNR. The reason is that higher elevation angles lead to higher signal power received. In case of receiving the same SNR (Figure 5b), a surface with lower permittivity (lower soil moisture content) requires a signal from a higher elevation angle, compared with a higher permittivity surface.

3.2. Sensitivity to the Number of Estimators and Samples

XGBoost was performed on the data set, considering the input vectors ($SNRrh$, $Gr$ $Pn$, and $\theta$) and the output vectors ($permittivity$). Estimators are number of trees to fit and samples $n$ are the numbers of data used. Often the hardest part of solving a machine learning problem can be finding the right estimator for the job. Different estimators are better suited for different types of data and different problems. The figures illustrate the behavior of variable importance estimation for different $estimators$ (500, 4000) and samples, in order to check if the variable importance is still stable when the $estimators$ and the samples $n$ are changed. The samples $n$ were set to 2000 and 5000 (Figure 6).

In Figure 6, the value of the variable $SNRrh$ was the highest in these two plots. With the increase of numbers of $estimators$ from 500 to 4000, the value of $SNRrh$ decreased slightly. $Pn$ and $\theta$ increased. We increased the samples $n$ from 2000 to 5000. The variable $SNRrh$ shows the same behavior, and $P_n$, $\theta$ increased slightly. Compared Figure 6a,b, each column with the same samples $n$, $Pn$, and $\theta$ increased, and the value of $SNRrh$ became lower, but it was still the highest among the variables with a value of 0.4 (40%). In addition, the value of $\theta$ increased when the number of the $estimators$ and the samples increased but it was still the lowest with a value below 0.1 (10%). In any case, the order of the variable importance was clear and it shows the same importance in those four figures. This phenomenon reports that the value of the variable $\theta$ (elevation angle) was much lower than $Pn$ (receiver noise) and $G_r$ (receiver gain), which was around 0.1 (10%), indicating that the elevation angle made less contribution to the permittivity retrieval than the other variables. Furthermore, the received SNR was a predominant variable with a contribution over 40% during the permittivity retrieval.

3.3. Sensitivity to the Number of Col-Sample-Tree and Samples

The optimized parameter $col-sample-tree$ represents the portion of selecting features when building a tree in XGBoost. The choice of the $col-sample-tree$ can be important for the variable importance estimation. As we showed above, the XGBoost algorithm was performed on the data set considering the input vectors ($SNRrh$, $Gr$ $Pn$, and $\theta$) and the output vectors ($permittivity$). The figures illustrate the behavior of variable importance estimation for different $col-sample-tree$ (0.5, 0.6) and samples $n$. We tried to check if the variable importance was still stable when the parameters were changed in this case. The samples $n$ were set to 2000 and 5000 (Figure 7) respectively.

The optimization of parameters can help with differentiating the significant variable and increase the stability of the variable importance estimation. In this case, the value of $SNRrh$ was the highest that was also observed in Figure 7a. When $n$ = 2000, $col-sample-tree$ increased from 0.5 to 0.6, $SNRrh$ increased to a value of 0.6. The value of $G_r$ decreased to 0.1 (10%). The value of $\theta$ also decreased to nearly zero. When the samples $n$ = 5000, the variables $SNRrh$ showed the same behavior with the case of $n$ = 2000, and the values of $G_r$ and $\theta$ (nearly zero) also decreased. If we increased the samples $n$ from 2000 to 5000, $Pn$ and $\theta$ increased little, and the value of $SNRrh$ decreased little, but the variable $SNRrh$ still showed the highest value among the variables in those plots. Furthermore, the value of $\theta$ is still the lowest value as mentioned before. In any case, the order of the variable importance was clear and quite stable in those four plots. This phenomenon also reported that the received SNR was predominate and the most sensitive parameter to the GNSS-R permittivity retrieval with the maximum contribution of 0.6 (60%). In addition, the value of the variable $\theta$ (elevation angle) was much lower than $Pn$ (receiver noise) and $G_r$ (receiver gain), which could be nearly zero indicating that the variable $\theta$ was not very sensitive to the output ($permittivity$) in this case. It also confirmed that it was a less sensitive input parameter in permittivity retrieval of GNSS-R.

3.4. Sensitivity to Different Types of Soil Compositions

The previous cases illustrate the importance and the sensitivity of the input variables for the permittivity retrieval in GNSS-R. The permittivity has a positive relationship with soil moisture content [54]. The relationship between soil permittivity and soil moisture is given by the soil permittivity models [54,55,56], so several static measurements were performed by the Remote Sensing Group at Politecnico di Torino in 2016. Among them, two typical types of soils that were chosen intentionally here to investigate the variable importance sensitivity for GNSS-R soil moisture content.

In

Table 1. Composition of the loamy sand soil (Grugliasco experiment) [53].

Coarse Sand (%)	Fine Sand (%)	Very Fine Sand (%)	Coarse Silt (%)	Fine Silt (%)	Clay (%)	Organic Matter (%)
15.5	50.1	16.1	5.3	8.2	4.8	1.4

and

Table 2. Composition of the silty clay loam soil (Agliano experiment) [53].

Coarse Sand (%)	Fine Sand (%)	Coarse Silt (%)	Fine Silt (%)	Clay (%)	Organic Matter (%)
1.1	10.5	6.4	44.5	36.8	0.7

, the composition (volume percentage and type of sand, clay) of the soil was reported in detail. According to the United States Department of Agriculture (USDA) Classification System, the two types of soil belong to the loamy sand and silty clay loam textural classes, respectively [59]. These different soil compositions that were used in the soil models for the permittivity to retrieve the soil moisture content here, and also for the subsequent ground-truth measurement.

The parameters of the sensitivity to the permittivity retrieval were studied in the previous case and showed that the order of the variable importance was clear and quite stable. In this case, we illustrated the sensitivity analysis for the input variables to soil moisture retrieval. The more samples $n$ we had, the results were more stable and precise, so the optimization parameters were $estimators$ = 2000, $n$ = 5000, regarding the parameter $col-sample-tree$ = 0.5 and 0.6 (Figure 8) respectively. In Figure 8, the loamy sand (a) and silty clay loam soil (b) case had similar behavior. The processed $SNR$ was the most sensitive parameter and the $\theta$ was the opposite. These variables in the two plots illustrated the same order as before. The highest contribution was observed when $col-sample-tree$ = 0.6, with the maximum of the importance of 0.7 (70%). The same as before, the value of the variable $\theta$ (elevation angle) was much lower than the $Pn$ (receiver noise) and $G_r$ (receiver gain), which denotes the minimum value of nearly zero indicating that the variable $\theta$ was almost not sensitive to the output (soil moisture content) in this case. It also confirms that it is a less important input parameter in soil moisture retrieval of GNSS-R.

3.5. Ground-Truth Experiment Data for Validation

Several ground-truth experiments were done in various test sites. Two sets of data particularly with two different typical soil compositions and soil moisture content (dry terrain and a wet terrain) were considered. Two ground-based campaigns with a controlled environment are shown in Figure 9. The first site is located in Grugliasco, Torino (45°03′58.5″N, 7°35′33.8″E), in the Dipartimento Inter-ateneo di Scienze Progetto e Politiche del Territorio (DIST) of Polito. In this place, a wide field of known characteristics (mainly 50% of sand) was available. The second site was located in Agliano (44°47′29.1″N, 8°15′19.8″E), where it is an area of smooth hills mainly devoted to wine production. In this second case, the composition of the soil is 50% silt and 37% clay. The details of the soil compositions for the two sites are reported in Table 1 and Table 2.

During the experiment, GNSS-R equipment and time-domain reflectometry (TDR) setup were used to make measurements before and after rain in bare fields. They were intentionally chosen due to their different terrain composition. The measurements in the dry condition were done after a long drought, and the wet condition was determined after several rainfalls. The timeline of the rainfall and the measurements are shown in Figure 10. The TDR measurement can provide a high spatial resolution between 1.0 and 2.0 cm for SMC between 10% and 40% [60] and reliable permittivity profiles that would be used in the GNSS-R performance analysis [61,62].

The GNSS-R system consists of two commercial frontends connected to two antennas and PCs for data acquisition. It was performed in bistatic GNSS-R configuration, which has one right-hand (RH) antenna pointing to the sky for receiving the direct signal and another left-hand (LH) antenna pointed downwards to receive the reflected signals in Figure 9. The antennas used in the experimental were two commercial antennas produced by ANTCOM Corp. that were able to receive the GNSS signals in L1 and L2 bands. Two commercial front-end SiGe GN3S v2 USB RF developed by the Colorado Center for Astrodynamics Research were used [63]. The front-end connected to the two antennas and a cable was used to transfer the sampled data to a PC. The antennas were mounted on a plastic tripod. The board was installed on the end of the bar that was kept horizontal at a height of 1.45 in both places (Grugliasco and Agliano). The acquisition of GPS data was performed by using N-Grab GNSS data grabber that was developed by the NavSAS group of Polito di Torino [64]. Then the raw data were post-processed for obtaining the SNR of each satellite. The reflected signals mainly contained the LH signal, and this measurement was done in the condition regardless of the surface roughness and incoherent components.

The values of the permittivity are obtained from local measurements based on time-domain reflectometry (TDR) technique [62]. A rod sensor (length 15 cm) Tektronix Metallic Cable Tester 1502 manufactured by Tektronix Inc., Beaverton, OR, USA, was used in the measurements (Figure 11). Then the value of permittivity was obtained from the travel time of the TDR probe. In this measurement, the position of the TDR probe was tilted to 30° with respect to the surface, thus, only around 7 cm of the surface were taken into account in the TDR measurements. This was done in order to satisfy the TDR results with those obtained with GNSS-R that sense only the first few centimeters of the surface (2–5 cm).

In the GNSS-R measurements, the major axis of the first Fresnel zone (the region surrounding the specular point from, which power is reflected with a phase change across the surface constrained to π radians, see Figure 1), for satellites in our geometrical condition (high elevation angle and a height of tripod of 1.5 m) was around 1 m. The TDR portable system was moved around to cover this area. Five measurements are performed with a cross scheme as shown in Figure 11 and the results are the averages of the five (black circles).

In the following, four campaigns are discussed in detail as shown in

Table 3. Summary of the experimental campaign.

Date	Soil Condition	Location	Soil Type
27 January 2016	Dry condition	Grugliasco	Loamy sand
5 February 2016	Dry condition	Agliano	Silty clay loam soil
3 March 2016	Wet condition	Grugliasco	Loamy sand
7 March 2016	Wet condition	Agliano	Silty clay loam soil

.

The traces of satellites in the sky during the experiment are plotted using different colors as shown in the skyplot of Figure 12. It shows the positions of satellites in terms of elevation and azimuth. The elevation was scaled by the concentric rings nested within one another. The outside ring was 0° and the middle of the plot was a 90° elevation. The azimuth is the direction angle with respect to the North (0°) measured clockwise. The sky plot for experiments in Grugliasco and Agliano was determined before each measurement to choose a proper system position and obtain the input variable ($\vartheta$). Especially, for static measurements, when the receiver is only a few meters high above the ground, the knowledge of the positions of the satellites and the first Fresnel zone coverage is sometimes crucial for analyzing the obtained data and provide the range of the data for comparing the results with other kinds of measurements. Here we also added the information of the position of the receiver and the direction that the bar was pointing to, which greatly helped with the GNSS-R retrieval analysis.

More than that, the georeferencing specular points on the x–y plane with Fresnel zones that relatively corresponded to each satellite, and the antenna footprint obtained at a height of 1.45 m (see Figure 9) was depicted by a big green circle, indicating the signal coverage of the antenna. The receiver projection was at the origin of coordinate and it was represented by a red point. The corresponding ellipse Fresnel zones surrounded the receiver projection represented by different color ellipses. The x-axis represents the distance in meter in West–East direction and the y-axis represents the distance in South–North direction. The antenna footprint will change accordingly with the azimuth and elevation angles, which makes it useful for planning a measurement aiming at receiving reflection signals from certain PRNs. In this measurement, this information is quite useful for the GNSS-R measurement and also indicating the location of the TDR instrument probe to precisely evaluate the permittivity as shown in Figure 13.

The obtained GNSS-R and TDR results with time series are shown in Figure 13. A good correlation between the GNSS-R and the TDR measurements with a certain PRN in each case can be observed. We have to note that the expected value is obtained from the PRN of which predicted Fresnel zones are in the green circle of the footprint (see Figure 12). Meanwhile, the TDR measurements were also implemented in this footprint. For the other satellites, the unexpected values could be ascribed to some interferences caused by the relative position of this satellite and the receiving antenna.

The statistical characterization of the GNSS-R and TDR estimates is shown in

Table 4. Statistical characterization of the GNSS-R and TDR estimates on Grugliasco (dry).

Meas		Permittivity		SMC
		GNSS-R	TDR	GNSS-R	TDR
PRN23	Median	5.5000	6.4579	0.0937	0.1150
	Mean	5.5833	6.4114	0.0954	0.1139
	Std	0.6686	0.3150	0.0150	0.0067

,

Table 5. Statistical characterization of the GNSS-R and TDR estimates on Agliano (dry).

Meas		Permittivity		SMC
		GNSS-R	TDR	GNSS-R	TDR
PRN13	Median	14.5000	15.2620	0.2771	0.2871
	Mean	14.5000	15.4418	0.2763	0.2886
	Std	1.9272	1.8810	0.0252	0.0238

,

Table 6. Statistical characterization of the GNSS-R and TDR estimates on Grugliasco (wet).

Meas		Permittivity		SMC
		GNSS-R	TDR	GNSS-R	TDR
PRN15	Median	9.0000	9.0900	0.1636	0.1651
	Mean	8.8333	9.0184	0.1602	0.1634
	Std	0.9374	0.9432	0.0168	0.0168

and

Table 7. Statistical characterization of the GNSS-R and TDR estimates on Agliano (wet).

Meas		Permittivity		SMC
		GNSS-R	TDR	GNSS-R	TDR
PRN7	Median	20.0000	22.0280	0.3432	0.3648
	Mean	21.0000	21.8708	0.3531	0.3624
	Std	2.7080	2.5808	0.0287	0.0269

. In the TDR measurement of Grugliasco, an average value of 6 in the dry condition was calculated as shown. Then the soil moisture content of 11% was estimated by considering the average value of 6 for the permittivity and using the model reported in [61]. The value of 11% was low because the measurement was performed after a long period of drought. The soil moisture calculated was close to the minimum observable value in the experimental field, and was consistent with the results of [65]. After a rainy period of one week, the value of average permittivity was 9 that corresponded to a soil moisture of 16%. In the measurement of Agliano, the average relative permittivity evaluated with the TDR technique in dry condition was 15. After a rainy period of one week, the average measured permittivity value was also 22 that corresponded to a soil moisture of 28% and 36%, respectively. The standard deviation of permittivity obtained in Agliano was obviously greater than the case of Gruglisco. One reason could be that the roughness of the Agliano is larger than the Grugliasco (see Figure 9); another reason could be the complex environment of Agliano site (e.g., some sand, dust, and rock may fly into the site from the nearby high-way).

The most traditional method of analyzing the quality of the soil moisture is the statistics methods (e.g., linear robust fit) [35,38]. We also tested the correlation using the linear fitting function as follows:

All the elevation angles of different PRNs were taken into account so a polynomial fitting with two input variables (three dimensional) are needed. The data of GNSS-R experiments (all elevation angle, SNR…) and the TDR measurement (Figure 13) were collected together for analyzing the permittivity (Figure 14) and SMC (Figure 15) variation with respect to the variables $\theta$ and the $SNR$ as shown. In these four plots, each black point stands for one elevation angle, corresponding SNR and the permittivity obtained from the TDR measurement of Grugliasco and Agliano. In each plot, we aimed to obtain the slope that indicates the variation rate of permittivity and SMC to different variables ($SNR$, $\theta$) when the soil changed from dry to wet.

In each plot, the variation rate (slope) with respect to $SNR$ was higher than $\theta$. The largest sensitivity of SNR to SMC could be observed in the case of Grugliasco (Figure 15a), which showed the sensitivity to SM, 3.8 dB/% (slope = 0.26). This linear fitting indicates that the variable $SNR$ was more sensitive to SMC retrieval than the variable $\theta$ (elevation angle). The results showed good correlation with the conclusion when the XGBoost were performed on the simulated data set. Moreover, comparing the different soil types (loamy sand and silty clay loam), the linear equation to retrieve permittivity and SMC from elevation had good agreement of variation and also for the SNR for both sites. The variation rate (slope) with respect to $SNR$ in high permittivity condition (Figure 15b) was higher than the value in low permittivity (Figure 15a). It demonstrates that the same changes of received SNR led to much more permittivity variation in silty clay loam than in loamy sand soil. It also confirmed that the permittivity had a positive relationship with the soil moisture content [56].

4. Discussion

A major focus on GNSS-R soil moisture currently is to evaluate the sensitivity of different observables to SM. Previous work was mainly focused on satellite remote sensing of soil moisture, concerning the dataset from the newly launched satellites UK TechDemoSat-1 (in short TDS-1) and NASA CYGNSS (Cyclone Global Navigation Satellite System). The reflection power obtained from the spaceborne sensors was compared to SMAP/SMOS products. A strong, positive linear relationship was found existing between the reflective power/reflectivity and the SM [35,38], also reported in this paper. The correlation of different GNSS-R observables to SM was found conclusive on a global scale. Apparently, experiments of in-situ sensors with smaller spatial scale require more studies. Besides the spaceborne mission, the ground-truth experiment is also a commonly used and favorable tool to implement the GNSS-R application.

We focus on the evaluation of the region of interest for different types of terrains using the ground-truth measurement, to evaluate the effect of the influence of uncertainty of received SNR and the elevation angle to SM. From the GNSS-R bistatic retrieval perspective, the GNSS-R parameters were regarded as input data, and the TDR data were taken as the output for the linear fit process. We have to note that, especially, in the case of ground-truth measurement, there are some factors (e.g., the interference of the equipment, the behavior of the radiation patterns, and the complex environmental conditions) that will affect the received signal. The uncertainty of the input parameters (bias of the elevation angle and SNR) may lead to some bad retrieval results that sometimes are hard to interpret.

The in-situ GNSS-R measurement was done and the data were post-processed to obtain the permittivity and soil moisture content. We showed the correlation between the GNSS-R and TDR results. It was found that the good correlation between the TDR and SMC retrieval results concerned the satellite that the bar was directly pointing to. As we have mentioned before, the TDR measurements were done in the footprint of the antenna, which just corresponded to the Fresnel zone of the satellite that obtained the expected results. Future studies could be the evaluation of permittivity by TDR equipment implemented, which is implemented nearby or outside the footprint, to investigate the influence of the antenna pattern on SMC retrieval. Besides that, the differences of wave propagation, penetration depth and attenuation factor in the two sites need to be carefully considered before planning the ground-based measurement. The clay mineral can include “water” in its mineralogical network. This might be the reason why you could not retrieve the expected SMC, although many of them cause small bias. In particular, when the soil was saturated, the GPS can only sense one or two centimeters of the soil [29].

The most commonly used method of analyzing the quality of the soil moisture is a linear robust fit [35]. In order to reveal the potential relationship between incident angle, SNR and the SM, all the incident angles of satellites with corresponding SNR were collected to do the linear robust fit to show the dependence of the variables to SM. The input of the linear fit is the GNSS-R input data, and the output is the TDR results. The highest sensitivity of SNR to SMC (TDR) can be observed, being 3.84 dB/%, which was higher than reported [35] but it could be reasonable since all the satellites were taken into account in this paper and the output TDR values were very critical for only two sites. Unlike the previous research, the aim of this paper was to investigate the degree to which the retrieval performance can be influenced by the uncertainty of the input data. Different from the traditional approach, another purpose of this paper was to utilize the XGBoost algorithm for the GNSS-R data by adopting the data mining concept. Since machine learning algorithms attempt to dig out the implicit rules from a large amount of data, they can function as a tool to uncover a function, especially when this function is too complicated to be formally expressed. In this case, the input is sample data, and the output will be the expected result.

Some existing and proven machine learning and neural networks methods have emerged to establish the estimation model based on the correlation selected features and retrieve soil moisture from SMOS data [66,67]. Both machine learning and neural networks are of artificial intelligence. Machine learning and neural networks (aiming at more complex problems and big data) are methods of implementing artificial intelligence. Machine learning is a technique for data modeling. What is more profound is that it extracts the appropriate model from given data to explain and predict. Like some common statistical methods, machine learning is also a form of statistical learning method. A computer uses existing data to derive a model, and then uses the model to predict the result. We also used the latest published Random Forest method for accessing the variable importance as in the following figures.

The results (Figure 16, Figure 17 and Figure 18) obtained from the latest published Random Forest method [66] were similar to the case involving XGBoost. They also showed that SNR was the most sensitive variable among the input variables. The difference was that the values of importance differences between each variable from XGBoost were larger than the values from the Random Forest method. From the algorithm mechanism point of view, one reason could be that the Random Forest uses majority voting in the final output, while XGBoost accumulates all results from each step. Another reason may be that the Random Forest method is not sensitive to the optimize parameter, which is good for a beginner, and the XGBoost needs to spend time on the optimization work.

Compared to the traditional statistics method, the machine learning algorithm is simpler and more flexible, and it is a good tool to find the underlying rules and value of data even from vast amounts of data. The pros of this study were to use the features of XGBoost method, which is a recently developed ensemble machine learning method good at the variable selection in data mining to examine the characterization of the input variables in the GNSS-R soil moisture retrieval. It showed a good correlation with the statistical analysis of ground-truth measurements. It is worthwhile before establishing models and can also help with understanding the underlying GNSS-R phenomena and interpreting the data.

5. Conclusions

In this paper, the performance of the bistatic GNSS-R soil moisture retrieval was examined and analyzed on the basis of a machine learning aided method. We took the first step to utilize the feature of the XGBoost to analyze the input variable importance in GNSS-R, which has quite high operating efficiency and prediction accuracy. A simulation data set was built and used for testing and training. The range of the parameters was set as close as staying to the experimental situation. In the meaning time, several optimization parameters (estimators, samples, and col-sample-tree), also for different typical types of soil compositions were changed to verify the stability of the results. It was reported that the variable $SNR$ showed the highest contribution than the other variables ($\theta$, $P_n$, and $G^r$) in the GNSS-R input vectors, either when we retrieved the permittivity or obtained soil moisture content for different soil types. It means that the received SNR is a predominant variable and much more sensitive to the obtained permittivity and soil moisture content with the importance of minimum 40%, and a maximum of 70%. Moreover, the variable $\theta$ showed the least importance (below 10%) in the GNSS-R soil moisture retrieval. In some extremely case (changing the parameter of the algorithm), the importance of variable $\theta$ is nearly zero means that it is almost not sensitive to the obtained permittivity and soil moisture content. Whatever we adjusted the parameter of the algorithm, the order of the variable importance is quite stable.

Here we must note one point that the variable with low importance does not mean that it is not necessary for the retrieval procedure. For example, a variable with higher contribution and importance means that the accuracy of the value is quite crucial for retrieving in GNSS-R and this variable is quite sensitive and important for obtaining satisfying results. The uncertainty of a variable with high importance causes a higher bias than the variable with low importance. From a practical perspective, this is quite significant for interpreting data and solving the problem, particularly when doing the GNSS-R experiment and the retrieval results are unsatisfying.

In order to further validate and discriminate the characteristics of the different input variables. Two GNSS-R ground-based campaigns with different soil conditions and compositions were carried out to do the performance analysis, which corresponds to the soil composition of the simulated data set. The permittivity of the ground-truth measurement was given by TDR measurement. The figure of skyplot provides information about the elevation angles. Combined the information of the GNSS-R and TDR measurement, we used a polynomial regression method to fit the input variables ($SNR$, $\theta$) with the permittivity and soil moisture results respectively, for evaluating the variation rate of retrieved results with respect to each input variable. It also showed that the input variable $SNR$ was a quite sensitivity parameter, which mostly impacts the soil moisture results than the variable $\theta$. For the two typical soil types, another conclusion was that the increasing rate of SMC (or permittivity) with respect to $SNR$ in silty clay loam soil (higher permittivity condition) was higher than in loamy sand soil (lower permittivity condition).

This paper focused on the understanding of the input variables importance through the XGBoost algorithm and the ground-truth measurement, to investigate the performance of the bistatic GNSS-R soil moisture retrieval method. The quantification of variables importance is not only an important issue for constructing a soil moisture retrieval model but also a critical issue in GNSS-R experiments to interpret data and understand the potential phenomena. Particularly, since the elevation angle $\theta$ determines the signal receiving for antennas, the finding of the paper is also helpful for the GNSS-R receiver construction and impact analysis. This finding also increases the understanding of our knowledge to the input variables and exploring the scope of the machine learning applied in GNSS-R.

Further studies will be conducted to monitor a region for a long period of time, to take seasonal effect into account, and to evaluate the sensitivity of the different observables to SM on a regional scale. Besides, more types of terrains could be added, and the areas of the experiments should be expanded. The findings of the paper show the importance of the SNR, and further analysis of in-situ data may provide more complete insight into how the received SNR can be used to retrieve SM [38].