Evaluation of Bayesian Multimodel Estimation in Surface Incident Shortwave Radiation Simulation over High Latitude Areas
Abstract
:1. Introduction
2. Data
2.1. CMIP5 GCMs
2.2. Ground Measurements
2.3. CERES EBAF SSR Retrievals
3. Methods
3.1. Bayesian Model Averaging (BMA) Method
3.2. Statistical Measures
3.2.1. Normalized RMSE
3.2.2. Nash–Sutcliffe Efficiency
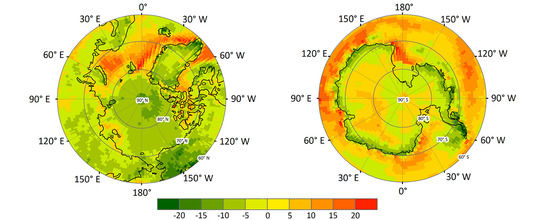
4. Results and Analysis
4.1. Evaluating CMIP5 GCMs SSR Simulations with Ground Measurements
4.2. Evaluating the MME Method Results with the Ground Measurements and the CERES EBAF Retrievals
4.3. Comparing and Evaluating the GCM Simulations and the MME Results with the CERES EBAF Retrievals
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, H.R.; Zhang, X.T.; Liang, S.L.; Yang, H.; Zhou, G.Q. Estimation of clear-sky land surface longwave radiation from MODIS data products by merging multiple models. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Zhang, X.T.; Liang, S.L.; Wang, G.X.; Yao, Y.J.; Jiang, B.; Cheng, J. Evaluation of the reanalysis surface incident shortwave radiation products from NCEP, ECMWF, GSFC, and JMA using satellite and surface observations. Remote Sens. 2016, 8, 225. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014–1017. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.K.; Ritchey, N.A.; Wilber, A.C.; Whitlock, C.H.; Gibson, G.G.; Stackhouse, P.W. A climatology of surface radiation budget derived from satellite data. J. Clim. 1999, 12, 2691–2710. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.T.; Liang, S.L.; Wild, M.; Jiang, B. Analysis of surface incident shortwave radiation from four satellite products. Remote Sens. Environ. 2015, 165, 186–202. [Google Scholar] [CrossRef]
- Abadi, A.M.; Oglesby, R.; Rowe, C.; Mawalagedara, R. Evaluation of GCMs historical simulations of monthly and seasonal climatology over Bolivia. Clim. Dyn. 2018, 51, 733–754. [Google Scholar] [CrossRef]
- Seiler, C.; Hutjes, R.W.A.; Kabat, P. Likely ranges of climate change in Bolivia. J. Appl. Meteor. Climatol. 2013, 52, 1303–1317. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, K.C.; Wild, M. Impact of geolocations of validation data on the evaluation of surface incident shortwave radiation from Earth System Models. J. Geophys. Res. Atmos. 2015, 120, 6825–6844. [Google Scholar] [CrossRef] [Green Version]
- Wild, M.; Folini, D.; Hakuba, M.Z.; Schaer, C.; Seneviratne, S.I.; Kato, S.; Rutan, D.A.; Ammann, C.; Wood, E.F.; Koenig-Langlo, G. The energy balance over land and oceans: An assessment based on direct observations and CMIP5 climate models. Clim. Dyn. 2015, 44, 3393–3429. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schar, C.; Loeb, N.; Dutton, E.G.; Konig-Langlo, G. The global energy balance from a surface perspective. Clim. Dyn. 2013, 40, 3107–3134. [Google Scholar] [CrossRef]
- Fang, M.; Li, X. Application of Bayesian model averaging in the reconstruction of past climate change using PMIP3/CMIP5 multimodel ensemble simulations. J. Clim. 2016, 29, 175–189. [Google Scholar] [CrossRef]
- Riihela, A.; Laine, V.; Manninen, T.; Palo, T.; Vihma, L. Validation of the Climate-SAF surface broadband albedo product: Comparisons with in situ observations over Greenland and the ice-covered Arctic Ocean. Remote Sens. Environ. 2010, 114, 2779–2790. [Google Scholar] [CrossRef]
- Boeke, R.C.; Taylor, P.C. Evaluation of the Arctic surface radiation budget in CMIP5 models. J. Geophys. Res. Atmos. 2016, 121, 8525–8548. [Google Scholar] [CrossRef]
- Frouin, R.; Franz, B.A.; Werdell, P.J. The SeaWiFS PAR product. NASA Tech. Memo. SeaWIFS Postlaunch Tech. Rep. Ser. 2003, 46–50. [Google Scholar]
- Riihela, A.; Key, J.R.; Meirink, J.F.; Munneke, P.K.; Palo, T.; Karlsson, K.G. An intercomparison and validation of satellite-based surface radiative energy flux estimates over the Arctic. J. Geophys. Res. Atmos. 2017, 122, 4829–4848. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, W.P.; Xia, J.Z.; Fisher, J.B.; Dong, W.J.; Zhang, X.T.; Liang, S.L.; Ye, A.Z.; Cai, W.W.; Feng, J.M. Using Bayesian model averaging to estimate terrestrial evapotranspiration in China. J. Hydrol. 2015, 528, 537–549. [Google Scholar] [CrossRef]
- Yao, Y.J.; Liang, S.L.; Li, X.L.; Hong, Y.; Fisher, J.B.; Zhang, N.N.; Chen, J.Q.; Cheng, J.; Zhao, S.H.; Zhang, X.T.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Miao, C.Y.; Duan, Q.Y.; Sun, Q.H.; Li, J.D. Evaluation and application of Bayesian multi-model estimation in temperature simulations. Prog. Phys. Geogr. 2013, 37, 727–744. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Hagedorn, R.; Palmer, T.N. The rationale behind the success of multi-model ensembles in seasonal forecasting—II. Calibration and combination. Tellus A 2005, 57, 234–252. [Google Scholar] [CrossRef]
- Stephenson, D.B.; Coelho, C.A.S.; Doblas-Reyes, F.J.; Balmaseda, M. Forecast assimilation: A unified framework for the combination of multi-model weather and climate predictions. Tellus A 2005, 57, 253–264. [Google Scholar] [CrossRef]
- Demirel, M.C.; Moradkhani, H. Assessing the impact of CMIP5 climate multi-modeling on estimating the precipitation seasonality and timing. Clim. Chang. 2016, 135, 357–372. [Google Scholar] [CrossRef]
- Miao, C.Y.; Duan, Q.Y.; Sun, Q.H.; Huang, Y.; Kong, D.X.; Yang, T.T.; Ye, A.Z.; Di, Z.H.; Gong, W. Assessment of CMIP5 climate models and projected temperature changes over Northern Eurasia. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y. Extreme climate events and agricultural climate indices in China: CMIP5 model evaluation and projections. Int. J. Climatol. 2016, 36, 43–61. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.Y.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Frohlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; Konig-Langlo, G.; McArthur, B.; Muller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New precision radiometry for climate research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Steffen, K.; Box, J.E.; Abdalati, W. Greenland Climate Network: GC-Net, CRREL 96–27 Special Report on Glaciers, Ice Sheets and Volcanoes; Colbeck, S.C., Ed.; Trib. To M. Meier; Greenland Climate Network: Boulder, CO, USA, 1996. [Google Scholar]
- Gilgen, H.; Wild, M.; Ohmura, A. Means and trends of shortwave irradiance at the surface estimated from global energy balance archive data. J. Clim. 1998, 11, 2042–2061. [Google Scholar] [CrossRef]
- Feng, F.; Wang, K.C. Merging satellite retrievals and reanalyses to produce global long-term and consistent surface incident solar radiation datasets. Remote Sens. 2018, 10, 115. [Google Scholar] [CrossRef]
- Box, J.E.; Steffen, K. Sublimation on the Greenland ice sheet from automated weather station observations. J. Geophys. Res. Atmos. 2001, 106, 33965–33981. [Google Scholar] [CrossRef]
- Wang, W.S.; Zender, C.S.; van As, D.; Miller, N.B. Spatial distribution of melt season cloud radiative effects over Greenland: Evaluating satellite observations, reanalyses, and model simulations against in situ measurements. J. Geophys. Res. Atmos. 2019, 124, 57–71. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Schar, C.; Muller, G.; Folini, D.; Schwarz, M.; Hakuba, M.Z.; Sanchez-Lorenzo, A. The Global Energy Balance Archive (GEBA) version 2017: A database for worldwide measured surface energy fluxes. Earth Syst. Sci. Data 2017, 9, 601–613. [Google Scholar] [CrossRef]
- Gilgen, H.; Ohmura, A. The global energy balance archive. Bull. Am. Meteorol. Soc. 1999, 80, 831–850. [Google Scholar] [CrossRef]
- Rahimikhoob, A.; Behbahani, S.M.R.; Banihabib, M.E. Comparative study of statistical and artificial neural network’s methodologies for deriving global solar radiation from NOAA satellite images. Int. J. Climatol. 2013, 33, 480–486. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; Van Tricht, K.; Lhermitte, S.; L’Ecuyer, T.S. Polar clouds and radiation in satellite observations, reanalyses, and climate models. Geophys. Res. Lett. 2017, 44, 3355–3364. [Google Scholar] [CrossRef]
- Kato, S.; Rose, F.G.; Rutan, D.A.; Thorsen, T.J.; Loeb, N.G.; Doelling, D.R.; Huang, X.L.; Smith, W.L.; Su, W.Y.; Ham, S.H. Surface irradiances of edition 4.0 clouds and the earth’s radiant energy system (CERES) energy balanced and filled (EBAF) data product. J. Clim. 2018, 31, 4501–4527. [Google Scholar] [CrossRef]
- Minnis, P.; Sun-Mack, S.; Young, D.F.; Heck, P.W.; Garber, D.P.; Chen, Y.; Spangenberg, D.A.; Arduini, R.F.; Trepte, Q.Z.; Smith, W.L.; et al. CERES Edition-2 cloud property retrievals using TRMM VIRS and Terra and Aqua MODIS data—Part I: Algorithms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4374–4400. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Rose, F.G.; Doelling, D.R.; Rutan, D.A.; Caldwell, T.E.; Yu, L.S.; Weller, R.A. Surface irradiances consistent with CERES-derived top-of-atmosphere shortwave and longwave irradiances. J. Clim. 2013, 26, 2719–2740. [Google Scholar] [CrossRef]
- Wilson, L.J.; Beauregard, S.; Raftery, A.E.; Verret, R. Calibrated surface temperature forecasts from the Canadian ensemble prediction system using Bayesian model averaging. Mon. Weather Rev. 2007, 135, 1364–1385. [Google Scholar] [CrossRef]
- Leamer, E.E. Regression selection strategies and priors. J. Am. Stat. Assoc. 1978, 73, 580–587. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. A 1922, 222, 309–368. [Google Scholar] [CrossRef] [Green Version]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Series B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Gleckler, P.J.; Taylor, K.E.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Li, J.L.F.; Waliser, D.E.; Stephens, G.; Lee, S.; L’Ecuyer, T.; Kato, S.; Loeb, N.; Ma, H.Y. Characterizing and understanding radiation budget biases in CMIP3/CMIP5 GCMs, contemporary GCM, and reanalysis. J. Geophys. Res. Atmos. 2013, 118, 8166–8184. [Google Scholar] [CrossRef]
- Glantz, P.; Bourassa, A.; Herber, A.; Iversen, T.; Karlsson, J.; Kirkevag, A.; Maturilli, M.; Seland, O.; Stebel, K.; Struthers, H.; et al. Remote sensing of aerosols in the Arctic for an evaluation of global climate model simulations. J. Geophys. Res. Atmos. 2014, 119, 20. [Google Scholar] [CrossRef]
- Hakuba, M.Z.; Folini, D.; Sanchez-Lorenzo, A.; Wild, M. Spatial representativeness of ground-based solar radiation measurements. J. Geophys. Res. Atmos. 2013, 118, 8585–8597. [Google Scholar] [CrossRef] [Green Version]
- Min, S.K.; Hense, A. A Bayesian approach to climate model evaluation and multi-model averaging with an application to global mean surface temperatures from IPCC AR4 coupled climate models. Geophys. Res. Lett. 2006, 33, 5. [Google Scholar] [CrossRef]
- Sloughter, J.M.; Raftery, A.E.; Gneiting, T.; Fraley, C. Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Mon. Weather Rev. 2007, 135, 3209–3220. [Google Scholar] [CrossRef]
- Wang, Q.J.; Schepen, A.; Robertson, D.E. Merging seasonal rainfall forecasts from multiple statistical models through Bayesian model averaging. J. Clim. 2012, 25, 5524–5537. [Google Scholar] [CrossRef]
- Yang, T.; Hao, X.B.; Shao, Q.X.; Xu, C.Y.; Zhao, C.Y.; Chen, X.; Wang, W.G. Multi-model ensemble projections in temperature and precipitation extremes of the Tibetan Plateau in the 21st century. Glob. Planet. Chang. 2012, 80–81, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.S.; Srinivasan, R.; Bosch, D. Calibration and uncertainty analysis of the SWAT model using genetic algorithms and Bayesian model averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Phillips, T.J. Bayesian estimation of local signal and noise in multimodel simulations of climate change. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]













| ID | Model Name | Institute ID | Country | Resolution |
|---|---|---|---|---|
| 1 | ACCESS1.0 | CSIRO-BOM | Australia | 1.88° × 1.24° |
| 2 | ACCESS1.3 | CSIRO-BOM | Australia | 1.88° × 1.24° |
| 3 | BCC-CSM1.1(m) | BCC | China | 1.13° × 1.13° |
| 4 | BCC-CSM1.1 | BCC | China | 2.81° × 2.81° |
| 5 | BNU-ESM | GCESS | China | 2.81° × 2.81° |
| 6 | CanCM4 | CCCMA | Canada | 2.81° × 2.81° |
| 7 | CanESM2 | CCCMA | Canada | 2.81° × 2.81° |
| 8 | CCSM4 | NCAR | USA | 1.25° × 0.94° |
| 9 | CESM1-BGC | NSF-DOE-NCAR | USA | 1.25° × 0.94° |
| 10 | CESM1-CAM5 | NSF-DOE-NCAR | USA | 1.25° × 0.94° |
| 11 | CESM1-CAM5.1.FV2 | NSF-DOE-NCAR | USA | 2.50° × 1.88° |
| 12 | CESM1-FASTCHEM | NSF-DOE-NCAR | USA | 1.25° × 0.94° |
| 13 | CESM1-WACCM | NSF-DOE-NCAR | USA | 2.50° × 1.88° |
| 14 | CMCC-CESM | CMCC | Italy | 3.75° × 3.75° |
| 15 | CMCC-CMS | CMCC | Italy | 1.88° × 1.88° |
| 16 | CMCC-CM | CMCC | Italy | 0.75° × 0.75° |
| 17 | CNRM-CM5.2 | CNRM-CERFACS | France | 1.41° × 1.41° |
| 18 | CNRM-CM5 | CNRM-CERFACS | France | 1.41° × 1.41° |
| 19 | CSIRO-Mk3.6.0 | CSIRO-QCCCE | Australia | 1.88° × 1.88° |
| 20 | FGOALS-g2 | LASG-CESS | China | 2.81° × 3.00° |
| 21 | FIO-ESM | FIO | China | 2.81° × 2.81° |
| 22 | GFDL-CM2p1 | NOAA GFDL | USA | 2.50° × 2.00° |
| 23 | GFDL-CM3 | NOAA GFDL | USA | 2.50° × 2.00° |
| 24 | GFDL-ESM2G | NOAA GFDL | USA | 2.50° × 2.00° |
| 25 | GFDL-ESM2M | NOAA GFDL | USA | 2.50° × 2.00° |
| 26 | GISS-E2-H-CC | NOAA GISS | USA | 2.50° × 2.00° |
| 27 | GISS-E2-H | NOAA GISS | USA | 2.50° × 2.00° |
| 28 | GISS-E2-R-CC | NOAA GISS | USA | 2.50° × 2.00° |
| 29 | GISS-E2-R | NOAA GISS | USA | 2.50° × 2.00° |
| 30 | HadCM3 | MOHC | UK | 3.75° × 3.47° |
| 31 | HadGEM2-AO | NIMR/KMA | Korea/UK | 1.88° × 1.24° |
| 32 | HadGEM2-CC | MOHC | UK | 1.88° × 1.24° |
| 33 | HadGEM2-ES | MOHC | UK | 1.88° × 1.24° |
| 34 | INM-CM4 | UNM | Russia | 2.00° × 1.50° |
| 35 | IPSL-CM5A-LR | IPSL | France | 3.75° × 1.88° |
| 36 | IPSL-CM5A-MR | IPSL | France | 2.50° × 1.26° |
| 37 | IPSL-CM5B-LR | IPSL | France | 3.75° × 1.88° |
| 38 | MIROC-ESM-CHEM | MIROC | Japan | 2.81° × 2.81° |
| 39 | MIROC-ESM | MIROC | Japan | 2.81° × 2.81° |
| 40 | MIROC4h | MIROC | Japan | 0.56° × 0.56° |
| 41 | MIROC5 | MIROC | Japan | 1.41° × 1.41° |
| 42 | MPI-ESM-LR | MPI-M | Germany | 1.88° × 1.88° |
| 43 | MPI-ESM-MR | MPI-M | Germany | 1.88° × 1.88° |
| 44 | MPI-ESM-P | MPI-M | Germany | 1.88° × 1.88° |
| 45 | MPI-CGCM3 | MRI | Japan | 1.13° × 1.13° |
| 46 | MPI-ESM1 | NCC | Norway | 1.13° × 1.13° |
| 47 | NorESM1-ME | NCC | Norway | 2.50° × 1.88° |
| 48 | NorESM1-M | NCC | Norway | 2.50° × 1.88° |
| Network | Site Name | Latitude (°) | Longitude (°) | Elevation (m) |
|---|---|---|---|---|
| GC-NET | Swiss Camp | 69.57 N | 49.32 W | 1149 |
| GC-NET | Crawford Pt. | 69.88 N | 46.99 W | 2022 |
| GC-NET | NASA-U | 73.84 N | 49.50 W | 2369 |
| GC-NET | GITS | 77.14 N | 61.04 W | 1887 |
| GC-NET | Humboldt | 78.53 N | 56.83 W | 1995 |
| GC-NET | Summit | 72.58 N | 38.51 W | 3254 |
| GC-NET | TUNU-N | 78.02 N | 33.99 W | 2113 |
| GC-NET | DYE-2 | 66.48 N | 46.28 W | 2165 |
| GC-NET | JAR | 69.50 N | 49.68 W | 962 |
| GC-NET | Saddle | 66.00 N | 44.50 W | 2559 |
| GC-NET | South Dome | 63.15 N | 44.82 W | 2922 |
| GC-NET | NASA-E | 75.00 N | 30.00 W | 2631 |
| GC-NET | CP2 | 69.88 N | 46.99 W | 1990 |
| GC-NET | NGRIP | 75.31 N | 42.33 W | 2950 |
| GC-NET | NASA-SE | 66.48 N | 42.50 W | 2425 |
| GC-NET | KAR | 69.70 N | 33.00 W | 2579 |
| GC-NET | JAR2 | 69.42 N | 50.06 W | 568 |
| GC-NET | JAR3 | 69.39 N | 50.31 W | 283 |
| GC-NET | Aurora | 67.15 N | 47.29 W | 1798 |
| GC-NET | Petermann Gl. | 80.68 N | 60.23 W | 37 |
| GC-NET | PeterMann ELA | 80.09 N | 58.07 W | 965 |
| BSRN | Barrow | 71.32 N | 156.61 E | 8 |
| BSRN | Georg von Neumayer | 70.65 S | 8.25 W | 42 |
| BSRN | Ny-Ålesund | 78.93 N | 11.93 E | 11 |
| BSRN | South Pole | 89.98 S | 24.80 W | 2800 |
| BSRN | Syowa | 69.01 S | 39.59 E | 18 |
| GEBA | Oimyakon | 63.27 N | 143.15 E | 726 |
| GEBA | Vanavara | 60.33 N | 102.26 E | 259 |
| GEBA | Verkhoyansk | 67.55 N | 133.38 E | 137 |
| GEBA | Yakutsk | 62.08 N | 129.75 E | 103 |
| GEBA | Bergen | 60.40 N | 5.32 E | 45 |
| GEBA | Borlaenge | 60.43 N | 15.50 E | 153 |
| GEBA | Helsinki-Airport | 60.32 N | 24.97 E | 53 |
| GEBA | Jokioinen | 60.82 N | 23.50 E | 104 |
| GEBA | Jyvaskyla-Airpt. | 62.40 N | 25.68 E | 141 |
| GEBA | Kiruna | 67.85 N | 20.23 E | 505 |
| GEBA | Lerwick | 60.13 N | 1.18 W | 82 |
| GEBA | Lulea | 65.55 N | 22.13 E | 16 |
| GEBA | Oestersund | 63.18 N | 14.50 E | 876 |
| GEBA | Reykjavik | 64.13 N | 21.90 W | 52 |
| GEBA | Sodankyla | 67.37 N | 26.65 E | 178 |
| GEBA | Umea | 63.82 N | 20.25 E | 10 |
| GEBA | Utsjoki, Kevo | 69.75 N | 27.03 E | 107 |
| GEBA | Resolute | 74.72 N | 94.98 W | 67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, X.; Li, W.; Hou, N.; Wei, Y.; Jia, K.; Yao, Y.; Cheng, J. Evaluation of Bayesian Multimodel Estimation in Surface Incident Shortwave Radiation Simulation over High Latitude Areas. Remote Sens. 2019, 11, 1776. https://doi.org/10.3390/rs11151776
Zhang W, Zhang X, Li W, Hou N, Wei Y, Jia K, Yao Y, Cheng J. Evaluation of Bayesian Multimodel Estimation in Surface Incident Shortwave Radiation Simulation over High Latitude Areas. Remote Sensing. 2019; 11(15):1776. https://doi.org/10.3390/rs11151776
Chicago/Turabian StyleZhang, Weiyu, Xiaotong Zhang, Wenhong Li, Ning Hou, Yu Wei, Kun Jia, Yunjun Yao, and Jie Cheng. 2019. "Evaluation of Bayesian Multimodel Estimation in Surface Incident Shortwave Radiation Simulation over High Latitude Areas" Remote Sensing 11, no. 15: 1776. https://doi.org/10.3390/rs11151776
APA StyleZhang, W., Zhang, X., Li, W., Hou, N., Wei, Y., Jia, K., Yao, Y., & Cheng, J. (2019). Evaluation of Bayesian Multimodel Estimation in Surface Incident Shortwave Radiation Simulation over High Latitude Areas. Remote Sensing, 11(15), 1776. https://doi.org/10.3390/rs11151776