Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
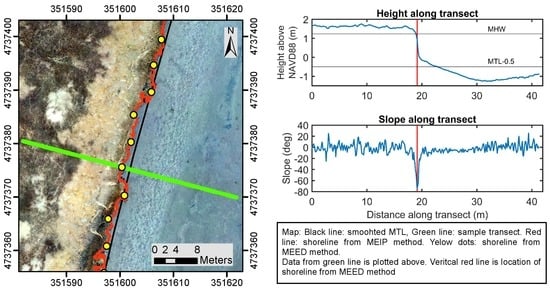
2.3. MEED Methodology
2.4. MEIP Methodology
2.5. Heads-Up Digitized Shoreline
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. UNEP Annual Report; United Nations Environmental Program: Nairobi, Kenya, 2006. [Google Scholar]
- Shepard, C.C.; Crain, C.M.; Beck, M.W. The Protective Role of Coastal Marshes: A Systematic Review and Meta-analysis. PLoS ONE 2011, 6, e27374. [Google Scholar] [CrossRef] [PubMed]
- Chmura, G.L.; Anisfeld, S.C.; Cahoon, D.R.; Lynch, J.C. Global carbon sequestration in tidal, saline wetland soils. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- Sousa, A.I.; Lillebø, A.I.; Pardal, M.A.; Caçador, I. Productivity and nutrient cycling in salt marshes: Contribution to ecosystem health. Estuar. Coast. Shelf Sci. 2010, 87, 640–646. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; Van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef] [Green Version]
- Gedan, K.B.; Silliman, B.R.; Bertness, M.D. Centuries of Human-Driven Change in Salt Marsh Ecosystems. Annu. Rev. Mar. Sci. 2009, 1, 117–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirwan, M.L.; Megonigal, J.P. Tidal wetland stability in the face of human impacts and sea-level rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Deegan, L.A.; Johnson, D.S.; Warren, R.S.; Peterson, B.J.; Fleeger, J.W.; Fagherazzi, S.; Wollheim, W.M. Coastal eutrophication as a driver of salt marsh loss. Nature 2012, 490, 388–392. [Google Scholar] [CrossRef]
- Holdredge, C.; Bertness, M.D.; Altieri, A.H. Role of crab herbivory in die-off of New England salt marshes. Conserv. Biol. 2009, 23, 672–679. [Google Scholar] [CrossRef]
- Craft, C.; Clough, J.; Ehman, J.; Joye, S.; Park, R.; Pennings, S.; Guo, H.; Machmuller, M. Forecasting the effects of accelerated sea-level rise on tidal marsh ecosystem services. Front. Ecol. Environ. 2008, 7, 73–78. [Google Scholar] [CrossRef]
- Weston, N.B. Declining Sediments and Rising Seas: An Unfortunate Convergence for Tidal Wetlands. Estuaries Coasts 2014, 37, 1–23. [Google Scholar] [CrossRef]
- Ganju, N.K.; Defne, Z.; Kirwan, M.L.; Fagherazzi, S.; D’Alpaos, A.; Carniello, L. Spatially integrative metrics reveal hidden vulnerability of microtidal salt marshes. Nat. Commun. 2017, 8, 14156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wigand, C.; Roman, C.T.; Davey, E.; Stolt, M.; Johnson, R.; Hanson, A.; Watson, E.B.; Moran, S.B.; Cahoon, D.R.; Lynch, J.C. Below the disappearing marshes of an urban estuary: Historic nitrogen trends and soil structure. Ecol. Appl. 2014, 24, 633–649. [Google Scholar] [CrossRef] [PubMed]
- Long, J.D.; Porturas, L.D. Herbivore impacts on marsh production depend upon a compensatory continuum mediated by salinity stress. PLoS ONE 2014. [Google Scholar] [CrossRef] [PubMed]
- Defne, Z.; Ganju, N.K. Unvegetated to Vegetated Marsh Ratio in Plum Island Estuary and Parker River Salt Marsh Complex, Massachusetts. Available online: https://www.sciencebase.gov/catalog/item/5b622a13e4b006a11f6f84c5 (accessed on 24 June 2019).
- Cowart, L.; Walsh, J.P.; Corbett, D.R. Analyzing estuarine shoreline change: A case study of Cedar Island, North Carolina. J. Coast. Res. 2010, 26, 817–830. [Google Scholar] [CrossRef]
- McLoughlin, S.M.; Wiberg, P.L.; Safak, I.; McGlathery, K.J. Rates and Forcing of Marsh Edge Erosion in a Shallow Coastal Bay. Estuaries Coasts 2015, 38, 620–638. [Google Scholar] [CrossRef]
- Currin, C.; Davis, J.; Cowart, L.; Malhotra, A.; Fonseca, M. Shoreline Change in the New River Estuary, North Carolina: Rates and Consequences. J. Coast. Res. 2015, 31, 1069–1077. [Google Scholar] [CrossRef]
- Graham, D.; Sault, M.; Bailey, C.J. National Ocean Service Shoreline—Past, Present, and Future. J. Coast. Res. 2003, 19, 14–32. [Google Scholar]
- White, S. Utilization of LIDAR and NOAA’s vertical datum transformation tool (VDatum) for shoreline delineation. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–6. [Google Scholar]
- Schmid, K.A.; Hadley, B.C.; Wijekoon, N. Vertical accuracy and use of topographic LIDAR data in coastal marshes. J. Coast. Res. 2011, 27, 116–132. [Google Scholar] [CrossRef]
- Campbell, A.; Wang, Y. High Spatial Resolution Remote Sensing for Salt Marsh Mapping and Change Analysis at Fire Island National Seashore. Remote Sens. 2019, 11, 1107. [Google Scholar] [CrossRef]
- Kuleli, T.; Guneroglu, A.; Karsli, F.; Dihkan, M. Automatic detection of shoreline change on coastal Ramsar wetlands of Turkey. Ocean Eng. 2011, 38, 1141–1149. [Google Scholar] [CrossRef]
- White, S.M.; Madsen, E.A. Tracking tidal inundation in a coastal salt marsh with Helikite airphotos: Influence of hydrology on ecological zonation at Crab Haul Creek, South Carolina. Remote Sens. Environ. 2016, 184, 605–614. [Google Scholar] [CrossRef]
- Anders, F.J.; Byrnes, M.R. Accuracy of shoreline change rates as determined from maps and aerial photographs. Shore Beach 1991, 59, 17–26. [Google Scholar]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical Shoreline Change: Error Analysis and Mapping Accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Robertson, W.; Whitman, D.; Zhang, K.; Leatherman, S.P. Mapping Shoreline Position Using Airborne Laser Altimetry. J. Coast. Res. 2004, 20, 884–892. [Google Scholar] [CrossRef]
- Moore, L.J.; Ruggiero, P.; List, J.H. Comparing Mean High Water and High Water Line Shorelines: Should Proxy-Datum Offsets be Incorporated into Shoreline Change Analysis? J. Coast. Res. 2006, 22, 894–905. [Google Scholar] [CrossRef]
- Ruggiero, P.; List, J.H. Improving Accuracy and Statistical Reliability of Shoreline Position and Change Rate Estimates. J. Coast. Res. 2009, 25, 1069–1081. [Google Scholar] [CrossRef]
- Stockdon, H.; Sallenger, A.; List, J.; Holman, R. Estimation of Shoreline Position and Change Using Airborne Topographic Lidar Data. J. Coast. Res. 2002, 18, 502–513. [Google Scholar]
- Weber, K.M.; List, J.H.; Morgan, K.L. An Operational Mean High Water Datum for Determination of Shoreline Position from Topographic Lidar Data; Open File Report 2005–1027; U.S. Geological Survey: Reston, VA, USA, 2005.
- White, S.A.; Parrish, C.E.; Calder, B.R.; Pe’eri, S.; Rzhanov, Y. Lidar-derived national shoreline: Empirical and stochastic uncertainty analyses. J. Coast. Res. 2011, 27, 62–74. [Google Scholar] [CrossRef]
- Farris, A.S.; Weber, K.M.; Doran, K.S.; List, J.H. Comparing Methods Used by the U.S. Geological Survey Coastal and Marine Geology Program for Deriving Shoreline Position from Lidar Data; Open-File Report 2018–1121; U.S. Geological Survey: Reston, VA, USA, 2018. [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; Open-File Report 2018–1179; U.S. Geological Survey: Reston, VA, USA, 2018. [CrossRef]
- Gibbs, A.E.; Richmond, B.M. National Assessment of Shoreline Change—Historical Shoreline Change Along the North Coast of Alaska, US–Canadian Border to Icy Cape; Open-File Report 2015–1048; U.S. Geological Survey: Reston, VA, USA, 2015. [CrossRef]
- Himmelstoss, E.A.; Kratzmann, M.G.; Hapke, C.; Thieler, E.R.; List, J. The National Assessment of Shoreline Change: A GIS Compilation of Vector Shorelines and Associated Shoreline Change Data for the New England and Mid-Atlantic Coasts; Open-File Report 2010–1118; U.S. Geological Survey: Reston, VA, USA, 2010.
- Kratzmann, M.G.; Himmelstoss, E.A.; Ruggiero, P.; Thieler, E.R.; Reid, D. The National Assessment of Shoreline Shange—A GIS Compilation of Vector Shorelines and Associated Shoreline Change Data for the Pacific Northwest Coast; Open-File Report 2012–1007; U.S. Geological Survey: Reston, VA, USA, 2010. [CrossRef]
- McKee, K.L.; Patrick, W.H. The Relationship of Smooth Cordgrass (Spartina alterniflora) to Tidal Datums: A Review. Estuaries 1988, 11, 143–151. [Google Scholar] [CrossRef]
- Balke, T.; Stock, M.; Jensen, K.; Bouma, T.J.; Kleyer, M. A global analysis of the seaward salt marsh extent: The importance of tidal range. Water Resour. Res. 2016, 52, 3775–3786. [Google Scholar] [CrossRef] [Green Version]
- Friedrichs, C.T.; Perry, J.E. Tidal Salt Marsh Morphodynamics: A Synthesis. J. Coast. Res. 2001, 17, 7–37. [Google Scholar]
- Mariotti, G.; Fagherazzi, S. A numerical model for the coupled long-term evolution of salt marshes and tidal flats. J. Geophys. Res.-Earth Surf. 2010, 115, 15. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Kirwan, M.L.; Mudd, S.M.; Guntenspergen, G.R.; Temmerman, S.; D’Alpaos, A.; Koppel, J.; Rybczyk, J.M.; Reyes, E.; Craft, C.; et al. Numerical models of salt marsh evolution: Ecological, geomorphic, and climatic factors. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Van De Koppel, J.; Van Der Wal, D.; Bakker, J.P.; Herman, P.M.J. Self-Organization and Vegetation Collapse in Salt Marsh Ecosystems. Am. Nat. 2005, 165, E1–E12. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Gross, M.F.; Klemas, V. Remote Sensing of Coastal Wetlands. BioScience 1986, 36, 453–460. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of emergent and submerged wetlands: An overview. Int. J. Remote Sens. 2013, 34, 6286–6320. [Google Scholar] [CrossRef]
- Brown, W.W. Wetland mapping in New Jersey and New York. Photogramm. Eng. Remote Sens. 1978, 44, 303–314. [Google Scholar]
- Cowardin, L.M.; Carter, V.; Golet, F.C.; LaRoe, E.T. Classification of Wetlands and Deepwater Habitats of the United States; U.S. Department of the Interior, US Fish and Wildlife Service: Washington, DC, USA, 1979.
- Dahl, T.E. Status and Trends of Wetlands in the Conterminous United States 2004 to 2009; Fisheries and Habitat Conservation; US Department of the Interior, US Fish and Wildlife Service: Washington, DC, USA, 2011.
- Guo, M.; Li, J.; Sheng, C.; Xu, J.; Wu, L. A Review of Wetland Remote Sensing. Sensors 2017, 17, 777. [Google Scholar] [CrossRef]
- Yang, J.; Artigas, F.J. Mapping salt marsh vegetation by integrating hyperspectral and LiDAR remote sensing. In Remote Sensing of Coastal Environments; CRC Press: Boca Raton, FL, USA, 2009; pp. 173–187. [Google Scholar]
- Ballanti, L.; Byrd, B.K.; Woo, I.; Ellings, C. Remote Sensing for Wetland Mapping and Historical Change Detection at the Nisqually River Delta. Sustainability 2017, 9, 1919. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A.; Liu, T.; Morton, J.; Wilhelm, V.L. Object-based classification of wetland vegetation using very high-resolution unmanned air system imagery. Eur. J. Remote Sens. 2017, 50, 564–576. [Google Scholar] [CrossRef] [Green Version]
- Isaach, J.P.; Costa, C.S.B.; Rodriguez-Gallego, L.; Conde, D.; Escapa, M.; Gagliardini, D.A.; Iribarne, O. Distribution of salt marsh plant communities associated with environmental factors along a latitudinal gradient on SW Atlantic coast. J. Biogeogr. 2006, 33, 888–900. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P. Mapping salt-marsh land-cover vegetation using high-spatial and hyperspectral satellite data to assist wetland inventory. GIScience Remote Sens. 2014, 51, 483–497. [Google Scholar] [CrossRef]
- Lane, R.C.; Liu, H.; Autrey, C.B.; Anenkhonov, A.O.; Chepinoga, V.V.; Wu, Q. Improved Wetland Classification Using Eight-Band High Resolution Satellite Imagery and a Hybrid Approach. Remote Sens. 2014, 6, 12187–12216. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.; Brabyn, L.; Beard, C. Effects of class granularity and cofactors on the performance of unsupervised classification of wetlands using multi-spectral aerial photography. J. Spat. Sci. 2014, 59, 269–282. [Google Scholar] [CrossRef]
- Hopkinson, C.S.; Morris, J.T.; Fagherazzi, S.; Wollheim, W.M.; Raymond, P.A. Lateral Marsh Edge Erosion as a Source of Sediments for Vertical Marsh Accretion. J. Geophys. Res. Biogeosci. 2018, 123, 2444–2465. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. Critical width of tidal flats triggers marsh collapse in the absence of sea-level rise. Proc. Natl. Acad. Sci. USA 2013, 110, 5353–5356. [Google Scholar] [CrossRef] [Green Version]
- OCM Partners. U.S. Geological Survey CMGP LiDAR: Post Sandy (MA, NH, RI), 20170509 ed.; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. Available online: https://inport.nmfs.noaa.gov/inport/item/49846 (accessed on 23 March 2017).
- U.S. Geological Survey. High Resolution Orthoimagery. 2013. Available online: http://earthexplorer.usgs.gov (accessed on 13 April 2017).
- Ganju, N.K.; Brosnahan, S.M.; Sturdivant, E.J.; Pendleton, E.A.; Ackerman, S.D. Aerial Imagery from Unmanned Aerial Systems (UAS) Flights—Plum Island Estuary and Parker River NWR (PIEPR); U.S. Geological Survey Data Release: Reston, VA, USA, 2019. [CrossRef]
- Casella, E.; Rovere, A.; Pedroncini, A.; Stark, C.P.; Casella, M.; Ferrari, M.; Firpo, M. Drones as tools for monitoring beach topography changes in the Ligurian Sea (NW Mediterranean). Geo-Mar. Lett. 2016, 36, 151–163. [Google Scholar] [CrossRef]
- Lucieer, A.; Jong, S.M.D.; Turner, D. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Prog. Phys. Geogr. Earth Environ. 2013, 38, 97–116. [Google Scholar] [CrossRef]
- Warrick, J.A.; Ritchie, A.C.; Adelman, G.; Adelman, K.; Limber, P.W. New Techniques to Measure Cliff Change from Historical Oblique Aerial Photographs and Structure-from-Motion Photogrammetry. J. Coast. Res. 2016, 33, 39–55. [Google Scholar] [CrossRef]
- Sturdivant, J.E.; Lentz, E.E.; Thieler, E.R.; Farris, S.A.; Weber, M.K.; Remsen, P.D.; Miner, S.; Henderson, E.R. UAS-SfM for Coastal Research: Geomorphic Feature Extraction and Land Cover Classification from High-Resolution Elevation and Optical Imagery. Remote Sens. 2017, 9, 1020. [Google Scholar] [CrossRef]
- Hladik, C.; Alber, M. Accuracy assessment and correction of a LIDAR-derived salt marsh digital elevation model. Remote Sens. Environ. 2012, 121, 224–235. [Google Scholar] [CrossRef]
- Rogers, J.N.; Parrish, C.E.; Ward, L.G.; Burdick, D.M. Assessment of elevation uncertainty in salt marsh environments using discrete-return and full-waveform lidar. J. Coast. Res. 2016, 33, 107–122. [Google Scholar] [CrossRef]
- Bodansky, E.; Gribov, A.; Pilouk, M. Smoothing and Compression of Lines Obtained by Raster-to-Vector Conversion. In Graphics Recognition Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2002; pp. 256–265. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; SRI International: Menlo Park, CA, USA, 1965. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice hall: Englewood Cliffs, NJ, USA, 1988; Volume 6. [Google Scholar]
- Farris, A.S. Marsh Shorelines of the Massachusetts Coast from 2013–2014 Topographic Lidar Data; U.S. Geological Survey data release: Reston, VA, USA, 2018. [CrossRef]
- Millette, T.L.; Argow, B.A.; Marcano, E.; Hayward, C.; Hopkinson, C.S.; Valentine, V. Salt Marsh Geomorphological Analyses via Integration of Multitemporal Multispectral Remote Sensing with LIDAR and GIS. J. Coast. Res. 2010, 26, 809–816. [Google Scholar] [CrossRef]
- Goodwin, G.C.H.; Mudd, S.M.; Clubb, F.J. Unsupervised detection of salt marsh platforms: A topographic method. Earth Surf. Dyn. 2018, 6, 239–255. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Carniello, L.; Alpaos, L.; Defina, A. Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes. Proc. Natl. Acad. Sci. USA 2006, 103, 8337–8341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Defina, A.; Carniello, L.; Fagherazzi, S.; D’Alpaos, L. Self-organization of shallow basins in tidal flats and salt marshes. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef] [Green Version]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farris, A.S.; Defne, Z.; Ganju, N.K. Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sens. 2019, 11, 1795. https://doi.org/10.3390/rs11151795
Farris AS, Defne Z, Ganju NK. Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sensing. 2019; 11(15):1795. https://doi.org/10.3390/rs11151795
Chicago/Turabian StyleFarris, Amy S., Zafer Defne, and Neil K. Ganju. 2019. "Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery" Remote Sensing 11, no. 15: 1795. https://doi.org/10.3390/rs11151795
APA StyleFarris, A. S., Defne, Z., & Ganju, N. K. (2019). Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sensing, 11(15), 1795. https://doi.org/10.3390/rs11151795