Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT)
Abstract
:1. Introduction
2. Signal Model and Problem Formulation TomoSAR
2.1. Acquisition Model
2.2. Problem Formulation
3. Problem Solution
3.1. CS
3.2. CS-GLRT
- CS
- Spurious artifacts
- Underestimation of magnitude
- BF based GLRT
- Low resolution
- Side-lobe effect
- Potential positions detection by CS imaging. In this step, the nonsignificant spurious scatterers are cleaned to offer a priori information for the possible scatterers’ locations with super-resolution so as to separate the closely located targets. Often, the number of potential positions can be set aswhere K represents the predefined maximum number of scatterers, is the norm, i.e., the number of nonzero values, and means the normalized elevation profile reconstructed by CS. Here, threshold of zero and nonzero can be set as (corresponds to a noise capacity of 20 dB) and considers the other two possible outliers surrounding each scatterer. Exploiting the CS imaging, the problem to be solved is scaled down from M-dimension to -dimension. Empirically, K can be set as 3 and is around 10.
- Model order selection and parameter estimation. For each model order, , we search for the optimal from possible combinations so as to minimize the numerator in Equation (10) . After obtaining the testing value of in each step, we can do hypothesis test sequentially, as shown in the dotted box in Figure 4. Once the model order i is selected, the elevations are the ones corresponding to the minimum numerator under the decided hypothesis and the backscattered reflectivity profile can be obtained by LS means.
4. Simulated Results and Performance Assessment
4.1. Feasibility Check
4.2. Parameter Definition
4.3. Performance Assessment
5. Results on Real Data
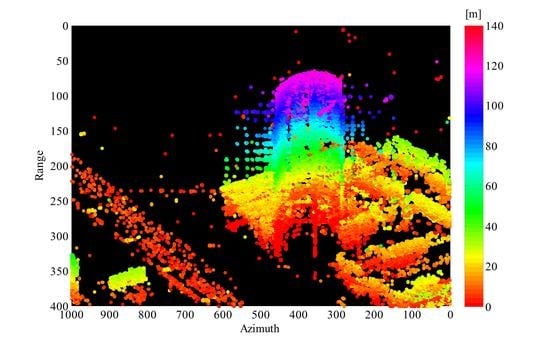
5.1. Test Site and Data Stack
5.2. Scatterers Detection
6. Discussion
6.1. CS-GLRT vs. SL1MMER
6.2. CS-GLRT vs. Sup-GLRT
6.3. Ghost Scatterers
7. Conclusions
- characteristic of CFAR, controlled by the adopted thresholds;
- accurate scatterer number detection as hypothesis test adopted;
- robustness to the nonuniform baseline distribution and super-resolution capability as CS imaging adopted; and
- small calculation increase with the increase of K as a priori information of provided by CS imaging.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | three-dimensional |
| AIC | Akaike information criterion |
| BF | beamforming |
| BIC | Bayes information criterion |
| CFAR | constant false alarm rate |
| CRLB | Cramer–Rao Low Bound |
| CS | compressive sensing |
| FAR | false alarm rate |
| GIS | geographic information systems |
| GLRT | generalized likelihood ratio test |
| IAA | iterative adaptive approach |
| IR-CS | iterative reweighted CS |
| IR-ADMM | iterative reweighted alternating direction method of multipliers |
| LS | least square |
| MC | Monte Carlo |
| MOS | model order selection |
| MUSIC | multiple signal classification |
| probability density function | |
| Pol-TomoSAR | polarimetric TomoSAR |
| PS | permanent scatterers |
| QCFAR | quasi-constant false alarm rate |
| RIP | restricted isometry property |
| RMSE | root mean square error |
| SAR | synthetic aperture radar |
| SLC | single look complex |
| SNR | signal-to-noise Ratio |
| sup-GLRT | support GLRT |
| SVD | singular value decomposition |
| TomoSAR | synthetic aperture radar tomography |
| TWIST | two-step iterative shrinkage/thresholding |
Appendix A
Appendix A.1.
Appendix A.2.

References
- Reigber, A.; Moreira, A. First Demonstration of Airborne SAR Tomography Using Multibaseline L-Band Data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2142–2152. [Google Scholar]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. Urban Tomographic Imaging Using Polarimetric SAR Data. Remote Sens. 2019, 11, 132. [Google Scholar] [Green Version]
- Zhu, X.X.; Yu, A.X.; Dong, Z.; Wu, M.Q.; Li, D.X.; Zhang, Y.S. New approach for robust and efficient detection of persistent in SAR tomography. Remote Sens. 2019, 11, 356. [Google Scholar]
- Martin del Campo, G.D.; Shkvarko, Y.V.; Reigber, A.; Nannini, M. TomoSAR Imaging for the Study of Forested Areas: A Virtual Adaptive Beamforming Approach. Remote Sens. 2018, 10, 1822. [Google Scholar] [Green Version]
- Li, X.W.; Liang, L.; Guo, H.D.; Huang, Y. Compressive Sensing for Multibaseline Polarimetric SAR Tomography of Forested Areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 153–166. [Google Scholar]
- Banda, F.; Dall, J.; Tebaldini, S. Single and Multipolarimetric P-Band SAR Tomography of Subsurface Ice Structure. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2832–2845. [Google Scholar]
- Yitayew, T.G.; Ferro-Famil, L.; Eltoft, T.; Tebaldini, S. Tomographic Imaging of Fjord Ice Using a Very High Resolution Ground-Based SAR System. IEEE Trans. Geosci. Remote Sens. 2017, 55, 698–714. [Google Scholar]
- She, Z.; Gray, D.; Bogner, R.; Homer, J. Three-dimensional SAR imaging via multiple pass processing. In Proceedings of the 1995 IEEE International Geoscience and Remote Sensing Symposium (IGARSS-95), Florance, Italy, 28 June–2 July 1995; Volume 5, pp. 2389–2391. [Google Scholar]
- Fornaro, G.; Serafino, F.; Soldovieri, F. Three-Dimensional Focusing With Multipass SAR Data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 507–517. [Google Scholar]
- Fornaro, G.; Lombardini, F.; Serafino, F. Three-dimensional multipass SAR focusing: Experiments with long-term spaceborne data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 702–714. [Google Scholar]
- Lombardini, F.; Pardini, M.; Fornaro, G.; Serafino, F.; Verrazzani, L.; Costantini, M. Linear and adaptive spaceborne three-dimensional SAR tomography: A comparison on real data. IET Radar Sonar Navig. 2009, 3, 424–436. [Google Scholar]
- Lombardini, F.; Pardini, M. Superresolution differential tomography: Experiments on identification of multiple scatterers in spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1117–1129. [Google Scholar]
- Kumar, S.; Joshi, S.K.; Govil, H. Spaceborne PolSAR Tomography for Forest Height Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5175–5185. [Google Scholar]
- Sauer, S.; Ferro-Famil, L.; Reigber, A.; Pottier, E. Three-Dimensional Imaging and Scattering Mechanism Estimation Over Urban Scenes Using Dual-Baseline Polarimetric InSAR Observations at L-Band. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4616–4629. [Google Scholar] [Green Version]
- Zhu, X.X.; Bamler, R. Tomographic SAR Inversion by L1 Norm Regularization - The Compressive Sensing Approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three-Dimensional SAR Focusing From Multipass Signals Using Compressive Sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar]
- Budillon, A.; Ferraioli, G.; Schirinzi, G. Localization Performance of Multiple Scatterers in Compressive Sampling SAR Tomography: Results on COSMO-SkyMed Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2902–2910. [Google Scholar]
- Maio, A.; Fornaro, G.; Pauciullo, A. Detection of Single Scatterers in Multidimensional SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2284–2297. [Google Scholar]
- Pauciullo, A.; Reale, D.; Maio, A.; Fornaro, G. Detection of Double Scatterers in SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3567–3586. [Google Scholar]
- Budillon, A.; Schirinzi, G. GLRT Based on Support Estimation for Multiple Scatterers Detection in SAR Tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1086–1094. [Google Scholar]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. A Fast Support Detector for Superresolution Localization of Multiple Scatterers in SAR Tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2768–2779. [Google Scholar]
- Budillon, A.; Johnsy, A.; Schirinzi, G. Extension of a Fast GLRT Algorithm to 5D SAR Tomography of Urban Areas. Remote Sens. 2017, 9, 844. [Google Scholar] [Green Version]
- Pauciullo, A.; Reale, D.; Franze, W.; Fornaro, G. Multi-Look in GLRT-Based Detection of Single and Double Persistent Scatterers. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5125–5137. [Google Scholar]
- Danis, C.; Fornaro, G.; Pauciullo, A.; Reale, D.; Datcu, M. Super-Resolution Multi-Look Detection in SAR Tomography. Remote Sens. 2018, 10, 1894. [Google Scholar] [Green Version]
- Zhu, X.X.; Bamler, R. Demonstration of Super-Resolution for Tomographic SAR Imaging in Urban Environment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3150–3157. [Google Scholar]
- Zhu, X.X.; Bamler, R. Super-Resolution Power and Robustness of Compressive Sensing for Spectral Estimation With Application to Spaceborne Tomographic SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 247–258. [Google Scholar]
- Peng, X.; Wang, C.C.; Li, X.W.; Du, Y.N.; Fu, H.Q.; Yang, Z.F.; Xie, Q.H. Three-Dimensional Structure Inversion of Buildings with Nonparametric Iterative Adaptive Approach Using SAR Tomography. Remote Sens. 2018, 10, 1004. [Google Scholar] [Green Version]
- Ma, P.; Lin, H.; Lan, H.; Chen, F. On the Performance of Reweighted L1 Minimization for Tomographic SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 895–899. [Google Scholar]
- Wang, X.; Xu, F.; Jin, Y.Q. The Iterative Reweighted Alternating Direction Method of Multipliers for Separating Structural Layovers in SAR Tomography. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1883–1887. [Google Scholar]
- Lianhuan, W.; Balz, T.; Zhang, L.; Liao, M. A Novel Fast Approach for SAR Tomography: Two-Step Iterative Shrinkage/Thresholding. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1377–1381. [Google Scholar]
- Zhu, X.X.; Ge, N.; Shahzad, M. Joint Sparsity in SAR Tomography for Urban Mapping. IEEE J. Sel. Top. Signal Proces. 2015, 9, 1498–1509. [Google Scholar] [Green Version]
- Donoho, D.; Stodden, V.; Tsaig, Y. SparseLab. Software, Version 2.1. 2007. Available online: http://sparselab.stanford.edu (accessed on 26 May 2007).
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Prentice-Hall: Englewood Cliffs, NJ, USA, 2005. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar]
- Zhu, X.X.; Bamler, R. Very High Resolution Spaceborne SAR Tomography in Urban Environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [Green Version]
- Adam, N.; Bamler, R.; Eineder, M.; Kampes, B. Parametric estimation and model selection based on amplitude-only data in ps-interferometry. In Proceedings of the ESA FRINGE Workshop, Frascati, Italy, 28 November–2 December 2005. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Serafino, F. Deformation monitoring over large areas with multipass differential SAR interferometry: A new approach based on the use of spatial differences. Int. J. Remote Sens. 2009, 30, 1455–1478. [Google Scholar]
- Donoho, D.L. De-Noising by soft thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M.; Kerkyacharian, G.; Picard, D. Wavelet shrinkage: Asymptopia? J. R. Stat. Soc. Ser. B 1995, 57, 301–369. [Google Scholar]















| Symbol | Description | Values |
|---|---|---|
| Sensor-to-target distance | 645,639 m | |
| f | Operating frequency | 9.65 GHz |
| Local incidence angle |
| Method | Super-Resolution | Computational Burden | CFAR/QCFAR |
|---|---|---|---|
| CS-GLRT | high | high | Yes |
| SL1MMER | high | high | No |
| Sup-GLRT | high | very high | Yes |
| M-Sup-GLRT | medium | low-medium | Yes |
| GLRT | low | low | Yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Li, Z.; Dong, Z.; Yu, A.; Zhang, Y.; Zhu, X. Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT). Remote Sens. 2019, 11, 1930. https://doi.org/10.3390/rs11161930
Luo H, Li Z, Dong Z, Yu A, Zhang Y, Zhu X. Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT). Remote Sensing. 2019; 11(16):1930. https://doi.org/10.3390/rs11161930
Chicago/Turabian StyleLuo, Hui, Zhenhong Li, Zhen Dong, Anxi Yu, Yongsheng Zhang, and Xiaoxiang Zhu. 2019. "Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT)" Remote Sensing 11, no. 16: 1930. https://doi.org/10.3390/rs11161930
APA StyleLuo, H., Li, Z., Dong, Z., Yu, A., Zhang, Y., & Zhu, X. (2019). Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT). Remote Sensing, 11(16), 1930. https://doi.org/10.3390/rs11161930