Development of a Parameterized Model to Estimate Microwave Radiation Response Depth of Frozen Soil
Abstract
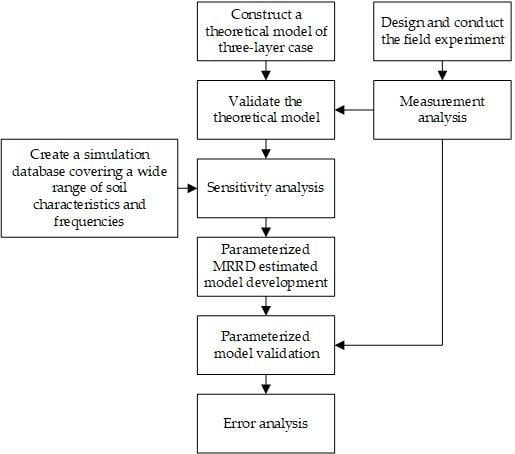
:1. Introduction
2. Materials and Methods
2.1. Field Experiment
2.1.1. Experimental Setup and Material Preparation
2.1.2. Measurements
2.2. Methodology
2.2.1. Microwave Radiation Response Depth (MRRD)
2.2.2. Theoretical Model
2.2.3. Sensitivity Analysis
2.2.4. Parameterized MRRD Estimated Model Development
3. Results
3.1. Measurement Results
3.2. Theoretical Model Validation
3.3. Parameterized Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kurganova, I.; Teepe, R.; Loftfield, N. Influence of freeze-thaw events on carbon dioxide emission from soils at different moisture and land use. Carbon Balance Manag. 2007, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Ou, Y.H.; Xu, X.; Zhao, L.; Song, M.; Zhou, C. Effects of permafrost degradation on ecosystems. Acta Ecologica Sinica 2010, 30, 33–39. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, W.; Liu, J.; Hu, X. Dynamics of greenhouse gas formation in relation to freeze/thaw soil depth in a flooded peat marsh of Northeast China. Soil Biol. Biochem. 2014, 75, 202–210. [Google Scholar] [CrossRef]
- Zuerndorfer, B.; England, A.W. Radiobrightness decision criteria for freeze/thaw boundaries. IEEE Trans. Geosci. Remote Sens. 1992, 30, 89–102. [Google Scholar] [CrossRef]
- Judge, J.; Galantowicz, J.F.; England, A.W.; Dahl, P. Freeze/thaw classification for prairie soils using SSM/I radiobrightnesses. IEEE Trans. Geosci. Remote Sens. 1997, 35, 827–832. [Google Scholar] [CrossRef]
- Zhang, T.; Armstrong, R.L.; Smith, J. Investigation of the near-surface soil freeze-thaw cycle in the contiguous United States: Algorithm development and validation. J. Geophys. Res.-Atmos. 2003, 108, 8860. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, L.; Jiang, L.; Zhao, S.; Chai, L.; Jin, R. A new soil freeze/thaw discriminant algorithm using AMSR-E passive microwave imagery. Hydrol. Process. 2011, 25, 1704–1716. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Azarderakhsh, M.; Dunbar, R.S.; Moghaddam, M.; McDonald, K.C. Classification of Alaska Spring Thaw Characteristics Using Satellite L-Band Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 542–556. [Google Scholar]
- Zhang, L.; Zhao, T.; Jiang, L.; Zhao, S. Estimate of Phase Transition Water Content in Freeze-Thaw Process Using Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4248–4255. [Google Scholar] [CrossRef]
- Schwank, M.; Stahli, M.; Wydler, H.; Leuenberger, J.; Matzler, C.; Fluhler, H. Microwave L-band emission of freezing soil. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1252–1261. [Google Scholar] [CrossRef]
- Wigneron, J.; Chanzy, A.; de Rosnay, P.; Rudiger, C.; Calvet, J. Estimating the Effective Soil Temperature at L-Band as a Function of Soil Properties. IEEE Trans. Geosci. Remote Sens. 2008, 46, 797–807. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Chanzy, A.; Wigneron, J.P.; Kerr, Y.H. Effective soil moisture sampling depth of L-band radiometry: A case study. Remote Sens. Environ. 2010, 114, 995–1001. [Google Scholar] [CrossRef] [Green Version]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive. Volume 1—Microwave Remote Sensing Fundamentals and Radiometry; Remote Sensing A; Addison-Wesley Publishing Company: Boston, MA, USA, 1981; Volume 1, ISBN 0-201-10759-7. [Google Scholar]
- Zhou, F.; Song, X.; Leng, P.; Li, Z. An Effective Emission Depth Model for Passive Microwave Remote Sensing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 1752–1760. [Google Scholar] [CrossRef]
- Wilheit, T.T. Radiative Transfer in a Plane Stratified Dielectric. IEEE Trans. Geosci. Remote Sens. 1978, 16, 138–143. [Google Scholar] [CrossRef]
- Wang, J.R. Microwave emission from smooth bare fields and soil moisture sampling depth. IEEE Trans. Geosci. Remote Sens. 1987, 25, 616–622. [Google Scholar] [CrossRef]
- Blinn, J.C.; Conel, J.E.; Quade, J.G. Microwave emission from geological materials: Observations of interference effects. J. Geophys. Res. 1972, 77, 4366–4378. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P.; Chiarantini, L.; Coppo, P.; Gagliani, S.; Luzi, G. Multifrequency passive microwve remote sensing of soil moisture and roughness. Int. J. Remote Sens. 1993, 14, 467–483. [Google Scholar] [CrossRef]
- Newton, R.W.; Black, Q.R.; Makanvand, S.; Blanchard, A.J.; Jean, B.R. Soil Moisture Information and Thermal Microwave Emission. IEEE Trans. Geosci. Remote Sens. 1982, 20, 275–281. [Google Scholar] [CrossRef]
- Owe, M.; Van de Griend, A.A. Comparison of soil moisture penetration depths for several bare soils at two microwave frequencies and implications for remote sensing. Water Resour. Res. 1998, 34, 2319–2327. [Google Scholar] [CrossRef]
- Laymon, C.A.; Crosson, W.L.; Jackson, T.J.; Manu, A.; Tsegaye, T.D. Ground-based passive microwave remote sensing observations of soil moisture at S-band and L-band with insight into measurement accuracy. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1844–1858. [Google Scholar] [CrossRef]
- Pampaloni, P.; Paloscia, S.; Chiarantini, L.; Coppo, P.; Gagliani, S.; Luzi, G. Sampling depth of soil moisture content by radiometric measurement at 21 cm wavelength: Some experimental results. Int. J. Remote Sens. 1990, 11, 1085–1092. [Google Scholar] [CrossRef]
- Jackson, T.J.; Bindlish, R.; Cosh, M.H.; Zhao, T.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Moran, M.S.; Goodrich, D.C.; Kerr, Y.H.; et al. Validation of Soil Moisture and Ocean Salinity (SMOS) Soil Moisture Over Watershed Networks in the U.S. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1530–1543. [Google Scholar] [CrossRef]
- Al Bitar, A.; Leroux, D.; Kerr, Y.H.; Merlin, O.; Richaume, P.; Sahoo, A.; Wood, E.F. Evaluation of SMOS Soil Moisture Products Over Continental US Using the SCAN/SNOTEL Network. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1572–1586. [Google Scholar] [CrossRef]
- Dall’Amico, J.T.; Schlenz, F.; Loew, A.; Mauser, W. First Results of SMOS Soil Moisture Validation in the Upper Danube Catchment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1507–1516. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, J.; Zhang, Z.J.; Zhao, K.G. The Estimation of Dielectric Constant of Frozen Soil-Water Mixture at Microwave Bands. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003; Volume 4, pp. 2903–2905. [Google Scholar]
- Zhao, S.; Zhang, L.; Zhang, Y.; Jiang, L. Microwave emission of soil freezing and thawing observed by a truck-mounted microwave radiometer. Int. J. Remote Sens. 2012, 33, 860–871. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, X.; Rogier, V.; Zeng, Y.; Wen, J.; Wang, Z.; Mike, S.; Paolo, F.; Su, B. L-Band Microwave Emission of Soil Freeze-Thaw Process in the Third Pole Environment. IEEE Trans. Geosci. Remote Sens. 2017, 9, 5324–5338. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhang, Z. Design and Test of a New Truck-Mounted Microwave Radiometer for Remote Sensing Research. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2008), Boston, MA, USA, 7–11 July 2008; Volume 2, pp. 1192–1195. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-rayes, M.A. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Anderson, D.M.; Tice, A.R. Predicting unfrozen water contents in frozen soils from surface area measurements. Highw. Res. Rec. 1972, 12–18. [Google Scholar]
- Ersahin, S.; Gunal, H.; Kutlu, T.; Yetgin, B.; Coban, S. Estimating specific surface area and cation exchange capacity in soils using fractal dimension of particle-size distribution. GEODERMA 2006, 136, 588–597. [Google Scholar] [CrossRef]
- Nedeltchev, N.M. Thermal microwave emission depth and soil moisture remote sensing. Int. J. Remote Sens. 1999, 20, 2183–2194. [Google Scholar] [CrossRef]
- Guru, B.S.; Hiziroglu, H.R. Electromagnetic Field Theory Fundamentals; Cambridge University Press: Cambridge, UK, 2004; ISBN 0-521-83016-8. [Google Scholar]
- Chai, L.; Zhang, L.; Shi, J.C.; Wu, F. Equivalent scattering albedo estimation of cotton and soybean. J. Remote Sens. 2013, 17, 17–33. [Google Scholar]














| Parameters | Value |
|---|---|
| Temperature | 243.15 to 271.15 K(−30 to −2 °C) |
| Frequency | 4 to 40 GHz |
| Soil specific surface area | 37.442 to 253.042 m2/g |
| Unfrozen water content | 0.02 to 0.31 cm3/cm3 |
| Bulk density | 1.2 to 1.8 g/cm3 |
| Incident angle | 55° |
| Initial soil moisture | 0.433 cm3/cm3 |
| Samples Thickness(cm) | Observation Duration | The Lowest and Highest Temperature(K) |
|---|---|---|
| 0.18 | Jan.12th 21:45~Jan. 13th, 15:24 | 260.3 ~ 294.1 |
| 0.43 | Jan.13th 18:06~Jan. 14th, 16:10 | 263.3 ~ 288.7 |
| 0.63 | Jan.14th 17:52~Jan. 15th, 16:32 | 265.7 ~ 283.7 |
| 0.96 | Jan.15th 17:40~Jan. 16th, 15:56 | 267.5 ~ 275.9 |
| 1.06 | Jan.17th 17:30~Jan. 19th, 09:53 | 268.5 ~ 277.8 |
| Parameters | Value |
|---|---|
| Temperature | 268 K, 269 K, 270 K, 271 K, and 272 K |
| Frequency | 6.925, 10.65, 18.7, and 36.5 GHz |
| Soil texture | sand: 30.16%, silt: 48.85%, clay: 20.99% |
| Bulk density | 1.41 g/cm3 |
| Initial soil moisture | 0.433 cm3/cm3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Jiang, L.; Zhao, S.; Chai, L.; Li, Y.; Pan, Y. Development of a Parameterized Model to Estimate Microwave Radiation Response Depth of Frozen Soil. Remote Sens. 2019, 11, 2028. https://doi.org/10.3390/rs11172028
Zhang T, Jiang L, Zhao S, Chai L, Li Y, Pan Y. Development of a Parameterized Model to Estimate Microwave Radiation Response Depth of Frozen Soil. Remote Sensing. 2019; 11(17):2028. https://doi.org/10.3390/rs11172028
Chicago/Turabian StyleZhang, Tao, Lingmei Jiang, Shaojie Zhao, Linna Chai, Yunqing Li, and Yuhao Pan. 2019. "Development of a Parameterized Model to Estimate Microwave Radiation Response Depth of Frozen Soil" Remote Sensing 11, no. 17: 2028. https://doi.org/10.3390/rs11172028
APA StyleZhang, T., Jiang, L., Zhao, S., Chai, L., Li, Y., & Pan, Y. (2019). Development of a Parameterized Model to Estimate Microwave Radiation Response Depth of Frozen Soil. Remote Sensing, 11(17), 2028. https://doi.org/10.3390/rs11172028