Development and Intercomparison Study of an Atmospheric Motion Vector Retrieval Algorithm for GEO-KOMPSAT-2A
Abstract
:1. Introduction
2. Data
2.1. Datasets for Optimization of the GEO-KOMPSAT-2A Atmospheric Motion Vector (GK-2A AMV) Algorithm
2.2. Datasets Used for Intercomparisons of GK-2A and Meteostat Third Generation (MTG) AMV Algorithms
3. Methods
3.1. GK-2A AMV Retrieval Algorithm Descriptions
3.1.1. Target Selection
3.1.2. Height Assignment
3.1.3. Tracking
3.1.4. Quality Control
3.2. Verification Methods
4. Results
4.1. Optimization of the GK-2A AMV Algorithm
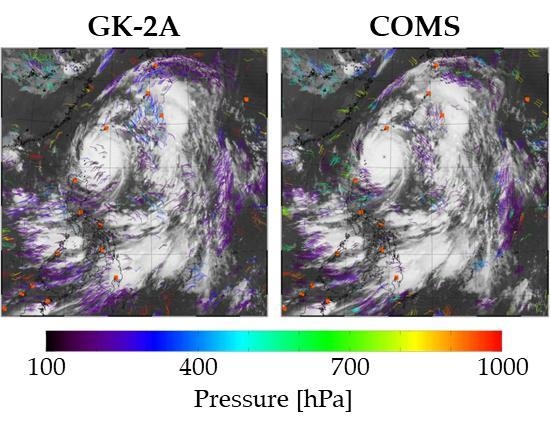
4.2. Comparison of GK-2A and Communication, Ocean and Meteorology Satellite (COMS) AMV Performances
4.3. Intercomparison of GK-2A and MTG AMVs
4.3.1. AMVs with CH13
4.3.2. AMVs with CH03, 07, 08, and 10
5. Discussion
5.1. Validation and Optimization of the GK-2A AMV Algorithm
5.2. Intercomparisons of GK-2A and MTG AMVs
5.3. Novelty and Limitations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Differences between GK-2A and MTG AMV Algorithms
| GK-2A AMV | MTG AMV | |
|---|---|---|
| Target box size | VIS: 48 by 48 Others: 16 by 16 | 16 by 16 (24 by 24) |
| Target center | Pixels with the largest standard deviation | Pixels with the largest standard deviation |
| Grid step size | Same with target box size | Same with target box size |
| Search box size | VIS: 201 by 201 Others: 54 by 54 | 54 by 54 (80 by 80) |
| Tracking | CC | CC |
| Height assignment | Cloudy target: CCC, EBBT, IR/WV intercept, and CO2 slicing Clear-air target: NTC and NTCC | Cloudy target: CCC Clear-air target: NTC, NTCC, and EBBT |
| Quality Control | QI, EE | QI |
| GK-2A QI | MTG QI | Common QI | |
|---|---|---|---|
, , , and | , , , and | , , and | |
, , , and | , , , , and | , , , and | |
, , , and | , , , and | , , and | |
, , , and | , , , and | , , and | |
, , , and for QI (WFC = 1.0 for QIF) | , , , and for QI (WFC = 1.0 for QIF) | , , and for CQI (WFC = 1.0 for CQIF) |
Appendix B. Performance according to Height Assignment Methods of GK-2A AMV Algorithm
| CCC | EBBT&IR/WV | EBBT | IR/WV | CO2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | |
| All levels (100–1000 hPa) | ||||||||||
| Number | 1,486,672 | 1,326,612 | 1,449,203 | 1,254,004 | 1,325,452 | 1,115,233 | 678,284 | 628,372 | 1,357,057 | 1,244,000 |
| MVD | 4.94 | 5.27 | 4.14 | 4.37 | 4.27 | 4.52 | 4.94 | 4.88 | 4.12 | 4.29 |
| RMSVD | 6.56 | 7.23 | 5.41 | 5.76 | 5.59 | 5.91 | 6.20 | 6.31 | 5.23 | 5.48 |
| Bias | −0.71 | −0.85 | 0.33 | 0.31 | 0.55 | 0.62 | 0.24 | 0.20 | −0.07 | 0.07 |
| RMSE | 5.23 | 5.98 | 4.06 | 4.38 | 4.19 | 4.44 | 4.64 | 4.69 | 3.91 | 4.07 |
| MSPD | 15.49 | 17.17 | 15.32 | 16.42 | 15.39 | 16.43 | 17.71 | 18.49 | 16.32 | 16.87 |
| High levels (100–400 hPa) | ||||||||||
| Number | 840,674 | 747,401 | 734,148 | 672,608 | 532,274 | 484,144 | 678,284 | 628,372 | 786,885 | 709,679 |
| MVD | 5.93 | 6.10 | 4.83 | 4.78 | 5.29 | 5.12 | 4.94 | 4.88 | 4.57 | 4.63 |
| RMSVD | 7.47 | 8.12 | 6.05 | 6.19 | 6.56 | 6.54 | 6.20 | 6.31 | 5.61 | 5.79 |
| Bias | −1.40 | −1.77 | 0.24 | 0.19 | 0.34 | 0.55 | 0.24 | 0.20 | −0.07 | −0.08 |
| RMSE | 5.94 | 6.69 | 4.53 | 4.61 | 4.88 | 4.71 | 4.64 | 4.69 | 4.15 | 4.21 |
| MSPD | 17.68 | 19.13 | 17.44 | 18.07 | 18.49 | 18.69 | 17.71 | 18.49 | 17.87 | 18.02 |
| Middle levels (400–700 hPa) | ||||||||||
| Number | 238,872 | 209,303 | 251,578 | 200,853 | 317,012 | 239,865 | - | - | 238,575 | 216,872 |
| MVD | 5.57 | 6.19 | 5.06 | 5.59 | 5.04 | 5.57 | - | - | 4.83 | 5.49 |
| RMSVD | 7.52 | 7.97 | 6.67 | 7.23 | 6.59 | 7.13 | - | - | 6.24 | 6.98 |
| Bias | −1.40 | −1.83 | −0.05 | −0.17 | 0.69 | 0.51 | - | - | −0.93 | −0.53 |
| RMSE | 6.27 | 6.94 | 5.22 | 5.89 | 5.17 | 5.81 | - | - | 4.93 | 5.62 |
| MSPD | 16.97 | 19.77 | 17.68 | 19.52 | 17.29 | 19.27 | - | - | 18.19 | 20.06 |
| Low levels (700–1000 hPa) | ||||||||||
| Number | 407,126 | 369,908 | 463,477 | 380,543 | 476,166 | 391,224 | - | - | 331,597 | 317,449 |
| MVD | 2.52 | 2.51 | 2.56 | 2.91 | 2.61 | 2.94 | - | - | 2.55 | 2.89 |
| RMSVD | 2.99 | 2.98 | 3.07 | 3.53 | 3.13 | 3.56 | - | - | 3.03 | 3.45 |
| Bias | 1.11 | 1.58 | 0.69 | 0.77 | 0.70 | 0.76 | - | - | 0.54 | 0.83 |
| RMSE | 2.01 | 2.01 | 2.06 | 2.42 | 2.10 | 2.45 | - | - | 2.03 | 2.31 |
| MSPD | 10.09 | 11.74 | 10.67 | 11.87 | 10.67 | 11.90 | - | - | 11.30 | 12.11 |
| CCC | EBBT & IR/WV | EBBT | IR/WV | CO2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | |
| All levels (100–1000 hPa) | ||||||||||
| Number | 83,148 | 77,797 | 79,179 | 71,497 | 74,819 | 68,925 | 61,418 | 50,244 | 79,135 | 70,147 |
| MVD | 6.22 | 7.04 | 4.88 | 5.38 | 5.26 | 5.62 | 4.99 | 5.18 | 4.90 | 5.25 |
| RMSVD | 7.76 | 8.70 | 6.09 | 7.03 | 6.44 | 7.07 | 6.21 | 6.76 | 6.01 | 6.76 |
| Bias | −1.08 | −1.00 | 0.47 | −0.18 | 0.23 | −0.24 | 0.43 | −0.11 | 0.30 | −0.05 |
| RMSE | 5.98 | 6.95 | 4.57 | 5.74 | 4.83 | 5.75 | 4.67 | 5.37 | 4.56 | 5.45 |
| MSPD | 16.12 | 17.02 | 15.87 | 17.92 | 16.33 | 17.75 | 16.68 | 18.53 | 16.67 | 16.93 |
| High levels (100–400 hPa) | ||||||||||
| Number | 74,321 | 70,237 | 68,112 | 56,152 | 63,067 | 51,788 | 61,418 | 50,244 | 68,930 | 55,182 |
| MVD | 6.43 | 7.24 | 4.96 | 5.12 | 5.46 | 5.37 | 4.99 | 5.18 | 4.98 | 5.38 |
| RMSVD | 7.95 | 8.91 | 6.16 | 6.67 | 6.64 | 6.59 | 6.21 | 6.76 | 6.10 | 6.96 |
| Bias | −1.19 | −1.23 | 0.44 | −0.08 | 0.17 | −0.10 | 0.43 | −0.11 | 0.32 | −0.28 |
| RMSE | 6.13 | 7.12 | 4.64 | 5.29 | 5.00 | 5.08 | 4.67 | 5.37 | 4.63 | 5.63 |
| MSPD | 16.72 | 17.06 | 16.51 | 18.24 | 17.27 | 18.04 | 16.68 | 18.53 | 17.14 | 17.08 |
| Middle levels (400–700 hPa) | ||||||||||
| Number | 4374 | 4150 | 6599 | 9124 | 7110 | 10,299 | - | - | 7018 | 7758 |
| MVD | 5.16 | 5.81 | 5.07 | 6.93 | 4.90 | 6.94 | - | - | 4.63 | 5.79 |
| RMSVD | 6.82 | 6.96 | 6.40 | 8.90 | 6.10 | 8.85 | - | - | 5.81 | 7.21 |
| Bias | −0.73 | 0.14 | 0.84 | −0.63 | 0.58 | −0.76 | - | - | −0.08 | 1.19 |
| RMSE | 5.44 | 5.69 | 4.76 | 7.77 | 4.57 | 7.75 | - | - | 4.33 | 5.80 |
| MSPD | 13.73 | 21.67 | 14.46 | 21.14 | 13.37 | 21.17 | - | - | 15.41 | 21.50 |
| Low levels (700–1000 hPa) | ||||||||||
| Number | 4453 | 3410 | 4468 | 6221 | 4642 | 6838 | - | - | 3187 | 7207 |
| MVD | 3.44 | 3.27 | 3.52 | 4.44 | 3.55 | 4.53 | - | - | 3.45 | 4.00 |
| RMSVD | 4.16 | 3.84 | 4.28 | 5.53 | 4.32 | 5.61 | - | - | 4.22 | 4.93 |
| Bias | 0.34 | 2.25 | 0.46 | −0.48 | 0.47 | −0.49 | - | - | 0.70 | 0.37 |
| RMSE | 2.97 | 2.73 | 3.07 | 4.33 | 3.10 | 4.37 | - | - | 3.02 | 3.79 |
| MSPD | 8.42 | 10.57 | 8.13 | 10.30 | 8.16 | 10.40 | - | - | 9.37 | 10.83 |
| NTC | NTCC | NTC & NTCC | ||||
|---|---|---|---|---|---|---|
| Period | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. |
| High levels (100–400 hPa) | ||||||
| Number | 129,345 | 117,342 | 184,248 | 150,169 | 188,629 | 152,996 |
| MVD | 4.68 | 4.73 | 4.75 | 4.80 | 4.58 | 4.67 |
| RMSVD | 6.28 | 6.60 | 6.34 | 6.68 | 6.09 | 6.39 |
| Bias | 0.33 | 0.18 | 0.37 | 0.23 | 0.28 | 0.12 |
| RMSE | 4.71 | 5.03 | 4.88 | 5.15 | 4.85 | 5.10 |
| MSPD | 19.42 | 20.51 | 18.98 | 19.84 | 19.04 | 19.89 |
| NTC | NTCC | NTC & NTCC | ||||
|---|---|---|---|---|---|---|
| Period | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. |
| High levels (100–400 hPa) | ||||||
| Number | 11645 | 9750 | 14515 | 10549 | 15170 | 10731 |
| MVD | 5.44 | 6.00 | 5.40 | 5.88 | 5.40 | 5.77 |
| RMSVD | 6.86 | 8.26 | 6.82 | 7.99 | 6.82 | 7.88 |
| Bias | 0.32 | 0.24 | 0.36 | 0.32 | 0.20 | 0.19 |
| RMSE | 5.24 | 6.46 | 5.27 | 6.17 | 5.24 | 6.13 |
| MSPD | 18.75 | 19.48 | 18.09 | 18.73 | 18.31 | 19.02 |
Appendix C. Comparisons of GDAPS and Era-Interim ECMWF Model Data
| ECMWF–GDAPS | GDAPS–Sonde | ECMWF–Sonde | |
|---|---|---|---|
| Number | 84,469 | 2800 | 2800 |
| MVD | 5.61 | 6.14 | 4.31 |
| RMSVD | 7.68 | 8.03 | 5.49 |
| Bias | 0.85 | −0.60 | −0.07 |
| RMSE | 5.77 | 5.14 | 3.73 |
References
- Menzel, W.P. Cloud Tracking with Satellite Imagery: From the Pioneering Work of Ted Fujita to the Present. Bull. Am. Meteorol. Soc. 2001, 82, 16. [Google Scholar] [CrossRef]
- Suomi, V.E.; Parent, R.J. A color view of planet earth. Bull. Am. Meteorol. Soc. 1968, 49, 74–75. [Google Scholar] [CrossRef]
- Oyama, R. Upgrade of atmospheric motion vector derivation algorithms at JMA/MSC. Meteorol. Satell. Cent. Tech. Note 2010, 50, 1–31. [Google Scholar]
- Otsuka, M.; Seko, H.; Shimoji, K.; Yamashita, K. Characteristics of Himawari—8 Rapid Scan Atmospheric Motion Vectors Utilized in Mesoscale Data Assimilation. J. Meteorol. Soc. Jpn. 2018, 96B, 111–131. [Google Scholar] [CrossRef]
- Shimoji, K. The development for MTSAT rapid scan high resolution AMVs at JMA/MSC. In Proceedings of the Tenth International Winds Workshop, Tokyo, Japan, 22–26 February 2010. [Google Scholar]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to meteosat second generation (msg). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Schmetz, J.; Holmlund, K.; Hoffman, J.; Strauss, B.; Mason, B.; Gaertner, V.; Koch, A.; Van De Berg, L. Operational Cloud-Motion Winds from Meteosat Infrared Images. J. Appl. Meteorol. 1993, 32, 1206–1225. [Google Scholar] [Green Version]
- Borde, R.; de Smet, A.; Dew, G.; Watts, P.; Lutz, H.-J.; Carranza, M.; Doutriaux-Boucher, M. AMV extraction algorithm in preparation for MTG. In Proceedings of the Eleventh International Winds Workshop, Auckland, New Zealand, 20–24 February 2012. [Google Scholar]
- Nieman, S.J.; Menzei, W.P.; Hayden, C.M.; Gray, D.; Wanzong, S.T.; Velden, C.S.; Daniels, J. Fully Automated Cloud—Drift Winds in NESDIS Operations. Bull. Am. Meteorol. Soc. 1997, 78, 1121–1134. [Google Scholar] [CrossRef]
- Daniels, J.; Bresky, W.; Wanzong, S.; Velden, C.; Berger, H. GOES-R Advanced Baseline Imager (ABI) Algorithm Theoretical Basis Document for Derived Motion Winds; Noaa Nesdis Center for Satellite Applications and Research; University of Wisconsin-Madison: Madison, WI, USA, 2019; p. 98. [Google Scholar]
- Daniels, J.; Velden, C.; Bresky, W.; Irving, A.; Turner, K. Status and development of GOES wind products at NOAA/NESDIS. In Proceedings of the 6th International Winds Workshop, Madison, WI, USA, 7–10 May 2002; pp. 71–80. [Google Scholar]
- Bedka, K.M.; Velden, C.S.; Petersen, R.A.; Feltz, W.F.; Mecikalski, J.R. Comparisons of Satellite-Derived Atmospheric Motion Vectors, Rawinsondes, and NOAA Wind Profiler Observations. J. Appl. Meteorol. Climatol. 2009, 48, 1542–1561. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.; Kim, Y.; Sohn, E.; Cotton, J.; Saunders, R. Application of hourly COMS AMVs in KMA operation. In Proceedings of the 11th International Winds Workshop, Auckland, New Zealand, 20–24 February 2012. [Google Scholar]
- Sohn, E.H.; Chung, S.R.; Park, J.S. Current status of COMS AMV in NMSC/KMA. In Proceedings of the 11th International Winds Workshop, Auckland, New Zealand, 20–24 February 2012; pp. 16–20. [Google Scholar]
- Lee, S.; Song, H.-J. Quantifying the inflation factors of observation error variance for COMS and MTSAT Atmospheric Motion Vectors considering spatial observation error correlation. Q. J. R. Meteorol. Soc. 2017, 143, 2625–2635. [Google Scholar] [CrossRef]
- Oh, Y.; Kim, J.H.; Park, H.; Baek, K. Development and Analysis of COMS AMV Target Tracking Algorithm using Gaussian Cluster Analysis. Korean J. Remote Sens. 2015, 31, 531–548. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.-S.; Ho, C.-H. Earth and environmental remote sensing community in South Korea: A review. Remote Sens. Appl. Soc. Environ. 2015, 2, 66–76. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Borde, R.; García-Pereda, J. Impact of Wind Guess on the Tracking of Atmospheric Motion Vectors. J. Atmos. Ocean. Technol. 2013, 31, 458–467. [Google Scholar] [CrossRef]
- García-Pereda, J.; Borde, R. The Impact of the Tracer Size and the Temporal Gap between Images in the Extraction of Atmospheric Motion Vectors. J. Atmos Ocean. Technol. 2014, 31, 1761–1770. [Google Scholar] [CrossRef] [Green Version]
- Cho, H.-J.; Sohn, E.-H.; Ou, M.-L. The impact of target box size on wind speed biases in satellite-derived atmospheric motion vectors. In Proceedings of the 2008 EUMETSAT Meteorological Satellite Conference, Darmstadt, Germany, 8–12 September 2008. [Google Scholar]
- Deb, S.K.; Wanzong, S.; Velden, C.S.; Kaur, I.; Kishtawal, C.M.; Pal, P.K.; Menzel, W.P. Height Assignment Improvement in Kalpana-1 Atmospheric Motion Vectors. J. Indian Soc. Remote Sens. 2014, 42, 679–687. [Google Scholar] [CrossRef]
- Borde, R.; Dubuisson, P. Sensitivity of Atmospheric Motion Vectors Height Assignment Methods to Semitransparent Cloud Properties Using Simulated Meteosat-8 Radiances. J. Appl. Meteorol. Climatol. 2010, 49, 1205–1218. [Google Scholar] [CrossRef]
- Nieman, S.J.; Schmetz, J.; Menzel, W.P. A Comparison of Several Techniques to Assign Heights to Cloud Tracers. J. Appl. Meteorol. 1993, 32, 1559–1568. [Google Scholar] [CrossRef]
- De Smet, A. AMV height assignment with Meteosat-9: Current status and future developments. In Proceedings of the 9th International Winds Workshop, Annapolis, MD, USA, 14–18 April 2008. [Google Scholar]
- Hocking, J.; Rayer, P.; Rundle, D.; Saunder, R.; Matricardi, M.; Geer, A.; Brunel, P.; Vidot, J. RTTOV v11 Users Guide; NWC SAF Report; Met Office: Exeter, UK, 2015. [Google Scholar]
- Fritz, S.; Winston, J.S. Synoptic use of radiation measurements from satellite tiros ii. Mon. Weather Rev. 1962, 90, 1–9. [Google Scholar] [CrossRef]
- Menzel, W.P.; Smith, W.L.; Stewart, T.R. Improved Cloud Motion Wind Vector and Altitude Assignment Using VAS. J. Clim. Appl. Meteorol. 1983, 22, 377–384. [Google Scholar] [CrossRef]
- Holz, R.E.; Ackerman, S.; Antonelli, P.; Nagle, F.; Knuteson, R.O.; McGill, M.; Hlavka, D.L.; Hart, W.D. An Improvement to the High-Spectral-Resolution CO2-Slicing Cloud-Top Altitude Retrieval. J. Atmos. Ocean. Technol. 2006, 23, 653–670. [Google Scholar] [CrossRef]
- Borde, R.; Doutriaux-Boucher, M.; Dew, G.; Carranza, M. A Direct Link between Feature Tracking and Height Assignment of Operational EUMETSAT Atmospheric Motion Vectors. J. Atmos. Ocean. Technol. 2013, 31, 33–46. [Google Scholar] [CrossRef]
- Holmlund, K. The Utilization of Statistical Properties of Satellite-Derived Atmospheric Motion Vectors to Derive Quality Indicators. Weather Forecast. 1998, 13, 1093–1104. [Google Scholar] [CrossRef]
- Imai, T.; Uesawa, D. Clear Sky Radiance (CSR) product derived from Himawari-8 data. Meteorol. Satell. Cent. Tech. Note 2016, 61, 53–58. [Google Scholar]
- Tokuno, M. Improvements in the method to extract operational cloud motion winds and water vapor motion winds of the GMS-5 system. In Proceedings of the 4th International Winds Workshop, Saanenmoser, Switzerland, 20–23 October 1998; pp. 61–68. [Google Scholar]
- Marshall, J.L.; Pescod, N.; Seaman, B.; Mills, G.; Stewart, P. An Operational System for Generating Cloud Drift Winds in the Australian Region and Their Impact on Numerical Weather Prediction. Weather Forecast. 1994, 9, 361–370. [Google Scholar] [CrossRef]
- MTG-FCI: ATBD for Atmospheric Motion Vector Product; EUMETSAT: Darmstadt, Germany, 2011.
- Le Marshall, J.; Rea, A.; Leslie, L.; Seecamp, R.; Dunn, M. Error characterisation of atmospheric motion vectors. Aust. Meteorol. Mag. 2004, 53, 123–131. [Google Scholar]
- Menzel, W.P. Report from the working group on verification statistics. In Proceedings of the Third International Winds Workshop, Ascona, Switzerland, 10–12 June 1996; pp. 17–19. [Google Scholar]
- Bresky, W.C.; Daniels, J.M.; Bailey, A.A.; Wanzong, S.T. New Methods Toward Minimizing the Slow Speed Bias Associated with Atmospheric Motion Vectors. J. Appl. Meteorol. Climatol. 2012, 51, 2137–2151. [Google Scholar] [CrossRef]









| AHI | AMI | |||||
|---|---|---|---|---|---|---|
| Channel Number | Central Wavelength [μm] | Band Width [μm] | Spatial Resolution [km] | Central Wavelength [μm] | Band Width [μm] | Spatial Resolution [km] |
| 1 | 0.455 | 0.05 | 1.0 | 0.470 | 0.041 | 1.0 |
| 2 | 0.510 | 0.02 | 1.0 | 0.509 | 0.029 | 1.0 |
| 3 | 0.645 | 0.03 | 0.5 | 0.639 | 0.081 | 0.5 |
| 4 | 0.860 | 0.02 | 1.0 | 0.863 | 0.034 | 1.0 |
| 5 | 1.61 | 0.02 | 2.0 | 1.37 | 0.015 | 2.0 |
| 6 | 2.26 | 0.02 | 2.0 | 1.61 | 0.041 | 2.0 |
| 7 | 3.85 | 0.22 | 2.0 | 3.83 | 0.19 | 2.0 |
| 8 | 6.25 | 0.37 | 2.0 | 6.21 | 0.84 | 2.0 |
| 9 | 6.95 | 0.12 | 2.0 | 6.94 | 0.40 | 2.0 |
| 10 | 7.35 | 0.17 | 2.0 | 7.33 | 0.18 | 2.0 |
| 11 | 8.60 | 0.32 | 2.0 | 8.59 | 0.35 | 2.0 |
| 12 | 9.63 | 0.18 | 2.0 | 9.62 | 0.38 | 2.0 |
| 13 | 10.45 | 0.30 | 2.0 | 10.35 | 0.47 | 2.0 |
| 14 | 11.20 | 0.20 | 2.0 | 11.23 | 0.66 | 2.0 |
| 15 | 12.35 | 0.30 | 2.0 | 12.36 | 1.11 | 2.0 |
| 16 | 13.30 | 0.20 | 2.0 | 13.29 | 0.57 | 2.0 |
| WSPD | WDIR | WVEC | WLC | WFC | |
|---|---|---|---|---|---|
| QI | 1 | 1 | 1 | 1 | 0 |
| QIF | 1 | 1 | 1 | 1 | 1 |
| CQI | 1 | 1 | 1 | 1 | 0 |
| CQIF | 1 | 1 | 1 | 1 | 1 |
| GK-2A | COMS | |||||||
|---|---|---|---|---|---|---|---|---|
| GDAPS | Rawinsonde | GDAPS | Rawinsonde | |||||
| Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | Jul. | Jan. | |
| All Levels (100–1000 hPa) | ||||||||
| Number | 812,874 | 766087 | 70163 | 61774 | 496981 | 549390 | 63573 | 49081 |
| MVD | 3.82 | 4.45 | 4.77 | 5.44 | 5.27 | 4.88 | 5.24 | 5.81 |
| RMSVD | 4.70 | 5.88 | 5.90 | 7.15 | 7.17 | 6.50 | 6.66 | 7.38 |
| Bias | −0.01 | −0.42 | −0.47 | −1.29 | 0.69 | −0.33 | −0.56 | −1.97 |
| RMSE | 3.42 | 4.50 | 4.41 | 5.89 | 5.18 | 4.91 | 4.95 | 6.05 |
| MSPD | 12.41 | 15.88 | 15.18 | 17.96 | 13.40 | 15.91 | 16.16 | 20.59 |
| GK-2A | COMS | |||
|---|---|---|---|---|
| GDAPS | Sonde | GDAPS | Sonde | |
| Number | 1654 (+44.8%) | 203 (+84.6%) | 1142 | 110 |
| MVD | 5.87 (−22.6%) | 4.67 (−3.9%) | 7.58 | 4.86 |
| RMSVD | 6.86 (−27.7%) | 5.84 (−8.6%) | 9.49 | 6.39 |
| Bias | 0.30 (−76.9%) | 0.50 (+6.38%) | 1.30 | 0.47 |
| RMSE | 4.59 (−24.4%) | 4.84 (−12.8%) | 6.07 | 5.55 |
| MSPD | 15.73 | 16.36 | 16.29 | 16.86 |
| GK-2A | MTG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Specific | Prescribed | Specific | Prescribed | |||||||||
| EBBT&IR/WV | CO2 Slicing | CCC | CCC | CCC | CCC | |||||||
| NWP | Sonde | NWP | Sonde | NWP | Sonde | NWP | Sonde | NWP | Sonde | NWP | Sonde | |
| Number | 75,963 | 2027 | 78,581 | 2356 | 73,252 | 1981 | 84,469 | 2800 | 43,845 | 1309 | 86,460 | 2957 |
| MVD | 5.44 | 5.86 | 5.44 | 5.70 | 5.67 | 7.02 | 4.44 | 5.80 | 4.35 | 5.67 | 4.54 | 5.76 |
| RMSVD | 7.53 | 8.19 | 7.35 | 7.69 | 7.64 | 8.66 | 5.98 | 7.64 | 5.87 | 7.29 | 6.19 | 7.52 |
| Bias | 0.58 | 0.59 | 0.07 | 0.33 | −0.89 | −0.93 | −0.26 | −0.45 | −0.31 | −0.59 | −0.14 | −0.43 |
| RMSE | 5.62 | 6.03 | 5.49 | 5.37 | 5.79 | 6.66 | 4.58 | 5.35 | 4.47 | 5.13 | 4.70 | 5.31 |
| MSPD | 14.39 | 13.62 | 14.71 | 14.07 | 14.41 | 15.59 | 14.51 | 14.66 | 13.96 | 14.84 | 13.92 | 14.13 |
| 03 | 07 | 08 | 10 | |||||
|---|---|---|---|---|---|---|---|---|
| NWP | Sonde | NWP | Sonde | NWP | Sonde | NWP | Sonde | |
| Number | 35,506 | 156 | 39,692 | 2018 | 51,787 | 2686 | 59,474 | 2945 |
| MVD | 4.45 | 6.52 | 4.24 | 5.71 | 5.28 | 5.90 | 5.15 | 5.97 |
| RMSVD | 6.08 | 7.38 | 5.89 | 7.68 | 6.80 | 7.76 | 6.68 | 7.80 |
| Bias | −0.56 | −0.37 | −0.76 | −0.80 | 0.37 | 0.21 | 0.30 | −0.02 |
| RMSE | 4.38 | 5.48 | 4.54 | 5.48 | 5.20 | 5.32 | 5.13 | 5.46 |
| MSPD | 12.24 | 14.12 | 13.88 | 13.49 | 15.72 | 15.77 | 16.92 | 16.33 |
| 03 | 07 | 08 | 10 | |||||
|---|---|---|---|---|---|---|---|---|
| NWP | Sonde | NWP | Sonde | NWP | Sonde | NWP | Sonde | |
| Number | 39,127 | 89 | 36,939 | 1706 | 54,775 | 2867 | 55,761 | 2939 |
| MVD | 4.47 | 6.24 | 4.28 | 5.75 | 5.47 | 6.27 | 5.28 | 5.88 |
| RMSVD | 6.11 | 7.17 | 5.87 | 7.75 | 6.84 | 8.16 | 6.62 | 7.95 |
| Bias | −0.75 | −0.71 | −0.67 | −0.89 | 0.95 | 0.97 | 0.62 | 0.52 |
| RMSE | 4.28 | 5.02 | 4.39 | 5.42 | 5.19 | 5.89 | 5.00 | 5.58 |
| MSPD | 11.13 | 13.46 | 13.14 | 13.35 | 15.48 | 16.38 | 14.97 | 15.35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, S.M.; Borde, R.; Carranza, M.; Shin, I.-C. Development and Intercomparison Study of an Atmospheric Motion Vector Retrieval Algorithm for GEO-KOMPSAT-2A. Remote Sens. 2019, 11, 2054. https://doi.org/10.3390/rs11172054
Oh SM, Borde R, Carranza M, Shin I-C. Development and Intercomparison Study of an Atmospheric Motion Vector Retrieval Algorithm for GEO-KOMPSAT-2A. Remote Sensing. 2019; 11(17):2054. https://doi.org/10.3390/rs11172054
Chicago/Turabian StyleOh, Soo Min, Régis Borde, Manuel Carranza, and In-Chul Shin. 2019. "Development and Intercomparison Study of an Atmospheric Motion Vector Retrieval Algorithm for GEO-KOMPSAT-2A" Remote Sensing 11, no. 17: 2054. https://doi.org/10.3390/rs11172054
APA StyleOh, S. M., Borde, R., Carranza, M., & Shin, I. -C. (2019). Development and Intercomparison Study of an Atmospheric Motion Vector Retrieval Algorithm for GEO-KOMPSAT-2A. Remote Sensing, 11(17), 2054. https://doi.org/10.3390/rs11172054