1. Introduction
Sea ice is an essential part of the Earth’s climate system [
1] and one of the indicators of global climate change. It plays an important role in heat exchange between the ocean and the atmosphere [
2]. Sea ice detection is very crucial for an accurate weather forecast [
3]. At the same time, sea ice is one of the causes of marine disasters in polar and high mid-latitude regions. An unusually large flux of polar sea ice will disrupt the balance of freshwater [
4], and affect the survival of living things [
5]. Sea ice at a mid-high latitude affects the human marine fishery [
6], coastal construction industry, and manufacturing industry, and also causes serious economic losses [
7]. In recent years, sea ice disasters have attracted more attention. Sea ice detection has important research significance [
8].
Sea ice detection needs to acquire effective data, and remote sensing technology has become an important means of analyzing and researching sea ice [
9] because of its characteristics of timeliness, accuracy, and large-scale data acquisition. The sea ice detection data commonly used include passive microwave [
10,
11], synthetic aperture radar (SAR) [
12,
13], multispectral satellite images with a medium or high spatial resolution (MODIS) [
14,
15], Landsat [
16], and hyperspectral images [
17]. Of these, hyperspectral remote sensing data has a large amount of data and many bands. It can obtain continuous, high-resolution one-dimensional spectral information, and two-dimensional spatial information of a target object. Hyperspectral images (HSIs) have the characteristics of a “merged image-spectrum,” and provide important data support for accurate sea ice classification. However, the high dimensionality and large data volume of hyperspectral data bring many problems (e.g., a strong correlation among bands, mixed redundant pixels, and data information redundancy), which easily lead to the Hughes phenomenon and become a problem of sea ice detection. In recent years, hyperspectral remote sensing technology has been gradually applied to the research of sea ice detection. Common methods include the conventional minimum distance, maximum likelihood, decision tree [
18], and the support vector machine (SVM) method [
19], based on the iterative self-organizing data analysis technique algorithm (ISODATA) [
20], linear prediction (LP) band selection [
21], and more. However, most of the above methods only use the spectral information in HSIs. It is difficult to solve the phenomenon of “different objects with the same spectrum” in hyperspectral sea ice detection using only spectral information, and the introduction of effective spatial information can make up for the deficiency of using only spectral information [
22], which can further improve the accuracy of sea ice classification. At present, the common spatial feature extraction methods are the gray-level co-occurrence matrix (GLCM) [
23,
24], Gabor filter [
25], and morphological profiles (MPs) [
26]. Among them, the statistical-based GLCM algorithm has a better application value because of its small feature dimension, strong discriminating ability, adaptability, and robustness [
2,
24]. However, these shallow and manual feature extraction methods based on expert experience and prior knowledge often ignore deep information, which limits the classification accuracy of HSIs.
In recent years, deep learning models have been well developed in the field of computer vision. Due to their characteristics from shallow to deep, from simple to complex, and independent of shallow artificial design, they can simultaneously extract the characteristics of deep spectral-spatial features, providing a new opportunity for the development of remote sensing technology. In 2014, for the first time in the field of remote sensing, an HSI classification method based on deep learning was introduced [
27]. The method uses a stacked autoencoder (SAE) to extract the hierarchical and robust features of HSIs and achieved good results. Subsequently, a large number of deep learning algorithms for HSI classification were proposed. These algorithms make full use of the characteristics of deep learning, in order to learn nonlinear, discriminative, and invariant features from the data autonomously, such as the deep belief network (DBN) [
28], the convolutional neural network (CNN) [
29], etc. The focus has also evolved from spectral and spatial features to spectral-spatial-joint features. CNN, as a local connection network, automatically learns the features with translation invariance from the input data through the convolution kernel, combines the represented features with the corresponding categories for joint learning, and adaptively adjusts the features to get the best feature representation [
30]. Additionally, hyperspectral data is usually represented by a three-dimensional data cube, which fits the input mode of extracting features from the three-dimensional convolution filter in CNN, and provides a simple and effective method for simultaneously extracting the features of spectral-spatial-combined features [
31]. Therefore, in recent years, CNN has been widely used in the field of HSI classification.
It is well-known that deep learning algorithms acquire discriminative and robust feature representations in repeated iterative processes, which require long training time and a large number of training samples to achieve the purpose of accurately identifying the type of object [
32]. Due to the particularity of the geographical environment of the sea ice covered area, it is difficult to obtain the actual land type information. It is necessary to manually label the sea ice type through prior knowledge. However, the labeling process is time consuming and costly. Due to the limited training samples and unpredictable sample quality, it is a challenge for deep learning algorithms to be applied to hyperspectral sea ice detection. To solve this problem, we improve the sample quality by combining the spectral-spatial information of unlabeled samples, reduce the cost of labeling, and realize sea ice detection based on deep learning using small samples. Therefore, our goal is to make full use of the spectral and spatial information of hyperspectral sea ice data and improve the accuracy of sea ice classification by using a deep learning method.
Based on the above research, this paper proposes a method for the classification of hyperspectral sea ice images based on spectral-spatial-joint features of deep learning, which combines three-dimensional CNN (3D-CNN) and the GLCM algorithm, enhances sample quality by making full use of the spectral-spatial information contained in neighboring, unlabeled samples of each pixel, and deep mines the spectral and spatial information of hyperspectral sea ice to further improve the accuracy of sea ice classification. Considering that 3D-CNN contains a large number of parameters to be trained, this paper utilizes the k-nearest neighbor (KNN) algorithm, which does not need any empirical parameters and is easy to implement, to select a certain number of unlabeled neighbor samples, and the information of unlabeled neighbor samples is used to enhance the quality of the labeled sample. However, the unlabeled sample also contains high-dimensional spectral information and redundant spatial information, which will burden the convolution operation of 3D-CNN. Therefore, in terms of the spectral information of unlabeled samples, based on our previous work [
21], we adopt the dimensionality reduction algorithm to select the optimal spectral band combination, according to its spectral characteristics. Furthermore, in terms of spatial information, we remove the spatial features with a high redundancy by correlation analysis [
33], and retain the low-correlation texture components for subsequent deep feature extraction, which reduces the burden of feature extraction in 3D-CNN as much as possible. Then, we compare the sea ice classification results with the existing National Snow and Ice Data Center (NSIDC,
http://nsidc.org/) data to verify the reliability of the proposed method.
The remainder of this paper is organized as follows.
Section 2 introduces the design framework and algorithm ideas in detail. The data set and related experimental setups are described in
Section 3, and the effects of experimental results and related parameters are discussed in
Section 4. Lastly, we summarize the work of this paper in
Section 5.
2. Proposed Method
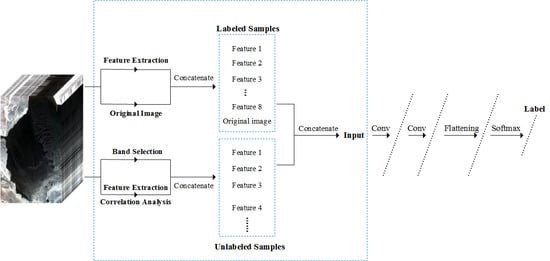
The framework of this proposed method is shown in
Figure 1. It consists of four main parts: GLCM-based spatial feature extraction, unlabeled sample data processing based on the band selection algorithm and correlation analysis, labeled sample enhancement that fuses neighboring unlabeled samples’ information, and spectral-spatial feature extraction and classification based on the 3D-CNN. First, the spatial features are extracted from the original HSI using GLCM, and the extracted spatial features are merged with the original data as the labeled sample data. The unlabeled sample data is obtained from the original data and the extracted spatial features by using the band selection algorithm and correlation analysis. Lastly, the labeled sample data and the unlabeled sample data are fused as the input of 3D-CNN, and the study of deep space-spectral features is then carried out. This algorithm will be described in subsequent sections.
2.1. Feature Extraction: Gray Level Co-Occurrence Matrix (GLCM)
Texture is defined by the fact that the gray value of the pixel in the image changes continuously, according to a certain rule in the spatial position. It is one of the most important visual cues for identifying various homogeneous regions, which helps to segment or classify images [
34].
A texture feature is a set of metrics computed by a feature extraction algorithm that is used to quantify the perceived texture of an image. Texture features are usually computed in a moving window, and each pixel in the image is set to an explicit and generic neighborhood set [
26]. The GLCM method extracts the texture feature information of an image by counting the grayscale attributes of each pixel and its neighborhood in the image, which are statistics of the frequency at which two pixels with a certain gray value on the image appear under a given offset distance, which lists the joint probability distribution of the pixel pair at different gray values. It can be expressed as follows.
In Equation (1), represents the set of quantized gray levels, d is the interval distance of pixel pairs, is the direction angle during the displacement process, is the relative coordinate of the pixel in the entire image, and are the horizontal and vertical offsets, respectively, and and are the columns and rows, respectively. represents the number of times that the pixel pair appears on the direction angle , where the gray values of the pixel pair are and , respectively.
Generally, four angles of 0°, 45°, 90°, and 135° are taken in the process of calculating GLCM, and the values corresponding to and are , , , and , respectively. Then, the eigenvalues in the four directions are averaged as a texture eigenvalue matrix.
The normalized gray level co-occurrence matrix can be expressed as follows.
In Equation (2), is the normalized representation of the elements in GLCM, is an element of GLCM, and and are the columns and rows of the image, respectively. Normally, if the texture of the image is relatively uniform, the larger values of the GLCM extracted from the image are gathered near the diagonal. If the texture of the image changes more sharply, the larger value of the GLCM will be distributed farther from the diagonal.
In this paper, eight texture scalars are extracted by GLCM to form textural feature bands, i.e., mean, variance, homogeneity, contrast, dissimilarity, entropy, angular second moment, and correlation [
24,
33].
2.2. Band Selection
Hyperspectral data dimensionality reduction maximizes the retention of important information in the data while compressing the original data. Preserving less spectral bands by the band selection algorithm not only better preserves the original features of the band, but also removes interference from redundant information, which reduces the computational cost in CNN.
In the band selection part of the algorithm in this paper, we used the content of the improved similarity measurement method based on the linear prediction (ISMLP) algorithm considering our previous work [
21]. The purpose of the algorithm is to select the optimal band combination with a great deal of information and low similarity between bands. The main idea is to determine the first initial band with the largest amount of information through mutual information (MI) and then select the second initial band by a spectral correlation measure (SCM). Then, subsequent band selection is performed by a linear prediction (LP) and the virtual dimension (VD) is used to estimate the minimum number of hyperspectral bands that should be selected.
2.3. 3D-CNN
Compared to one-dimensional convolutional neural network (1D-CNN) and two-dimensional convolutional neural network (2D-CNN) based on spectral features and spatial features, respectively, the 3D-CNN based on spectral-spatial-joint features takes into account the advantages of both and can simultaneously extract the spectral information and spatial information in HSI spontaneously. By initializing in an unsupervised manner, and then fine-tuning in a supervised manner, 3D-CNN constantly learns high-level features with abstraction and invariance from low-level features, which is conducive to classification, target detection, and other tasks.
In HSI classification, the 3D-CNN can map the input HSI pixels to the input pixel labels, so that each pixel in the HSI can obtain its category label through the network, and complete the pixel-level classification for HSI. In contrast, the 3D-CNN extracts the spectral-spatial information from the cube of the small spatial neighborhood centered on a certain pixel, and uses the category label obtained by the output layer as the label of the central pixel. Therefore, the input of the 3D-CNN is a three-dimensional cube block extracted from the HSI, and the pixel block size is K × K × B, where K is the spatial dimension of the pixel block and must be an odd number, and B is the size of the pixel block in the spectral dimension and is the number of bands of the HSI. The calculation formula for 3D-CNN is carried out as follows.
where
is the size of the 3D convolution kernel in the spectral dimension,
and
, respectively, represent the height and width of the 3D convolution kernel,
is the value at the
th feature cube of the
th layer at the position
,
represents the specific value of the
th convolution kernel of the
th layer at the position
, and the convolution kernel is connected to the
th feature cube of the
th layer, and
is biased while
is the activation function. In this paper, the
ReLU function is used as the activation function, which is beneficial to gradient descent and back propagation, and avoids the problem of gradient disappearance. The formula is shown below.
In addition, the Adaptive moment estimation (Adam) algorithm is used as the gradient optimization algorithm in this paper [
35]. The algorithm combines the advantages of the adaptive gradient algorithm (AdaGrad) to deal with the sparse gradient and root mean square prop algorithm (RMSProp) to deal with non-stationary targets. The first-order moment estimation and second-order moment estimation of the gradient are used to dynamically adjust the learning rate of each parameter, after offset correction, and update the different parameters. The specific expression is as follows.
First, assume that, at time
, the first derivative of the objective function for the parameter is
. Equations (5) and (6) are updates to the biased first-order moment estimate and the biased second-order moment estimate of the gradient. The deviation is corrected according to the gradient by Equations (7) and (8), and, lastly, the parameter update is completed by Equation (9).
In Equations (5)–(9), and are the exponential decay rates of the moment estimates, 0.9 and 0.999, respectively. and are first-order moments and second-order moment variables at time , and the initial values are all 0 while is the learning rate. To prevent the denominator’s value being 0, the value of the small constant is set to , and is the 3D-CNN parameter variable at time , including weights and offsets.
2.4. Implementation Process of the Proposed Method
According to the above algorithm, the specific algorithm implementation process is described as Algorithm 1 shown below.
| Algorithm 1: Proposed Method |
| Begin |
| Input: Original HSIs |
| A. Feature extraction |
| (1) Process the original data set by the principal component analysis (PCA) algorithm, taking the first principal component (PC). |
| (2) According to the GLCM algorithm, slide the sliding window on the PC by step d and direction angle , and calculate the gray level co-occurrence matrix of the sliding window every time it is slid, obtain the texture feature value, and then assign textural feature values to the center pixel of the window, |
| (3) Repeat (2) until the sliding window covers the PC, |
| (4) For a certain textural scalar, sum, and average the textural feature matrix of the four direction angles as the final textural feature matrix, and also do the same with other textural features, |
| (5) Repeat step (4) until eight textural features are obtained, |
| (6) Feature extraction is completed. |
| B. Nearest neighbor sample selection |
| (7) For a certain labeled sample in the original data, calculate the Euclidean distance with all unlabeled samples, and sorted into ascending order, its formula is as follows: , |
| (8) Repeat step (7) until all labeled samples have been calculated, |
| (9) Neighbor samples extraction is completed. |
| C. Input data preprocessing |
| i. Labeled samples |
| (10) Stack the spatial features extracted from the phase with the original data. |
| (11) The data acquisition of labeled samples is completed. |
| ii. Unlabeled samples |
| (12) Obtain spectral features by reducing the original data by the band selection method in Section 2.2. |
| (13) Obtain spatial features by correlation analysis of the spatial features extracted from phase A, and remove the highly correlated components. |
| (14) Stack spectral features and spatial features in steps (12) and (13). |
| (15) The data acquisition of unlabeled samples is completed. |
| (16) Fuse the labeled sample data in i(Labeled samples) with the unlabeled sample data in ii(Unlabeled samples) according to the neighbor relationship in phase B. |
| (17) Input data is completed. |
| D. 3D-CNN |
| (18): Input data is randomly divided into training samples and test samples, and the input size of each sample is K × K × B. |
| Training stage |
| (19) Randomly select Batch (Batch = 20) training samples from the training samples into the pre-established 3D-CNN network each time. |
| (20) Suppose the first layer contains n convolution kernels of size C × C × D. After each K × K × B sample is subjected to the convolution operation of the first layer, n data cubes of size (K-C+1) × (K-C+1) × (B-D+1) are output values. The output of the first layer is the input of the second layer, which continues the convolution operation, and more. The final output is converted into a feature vector and then input into the fully connected layer, with the mapping and merging of local features extracted during convolution. After calculating the loss rate by the Softmax cross entropy function, the gradient of each parameter is calculated by back propagation, and the network parameters are dynamically updated by the Adam algorithm. |
| (21) Repeat steps (19) and (20), until the preset number of iterations is completed. |
| (22) Model training is completed. |
| Test stage |
| (23) Input the test sample in step (18) into the trained 3D-CNN model, and calculate the confusion matrix according to the predicted label and the real label to get the classification accuracy. |
| (24) Test is finished. |
| Output: confusion matrix, overall accuracy, average accuracy, Kappa statistic. |
| End |
5. Conclusions
In hyperspectral remote sensing sea ice image classification, it is difficult to acquire labeled samples due to environmental conditions, and the labeling cost is high. In addition, most traditional sea ice classification methods only use spectral features, and do not make full use of the rich spatial features included in hyperspectral remote sensing sea ice images, which limits further improvement of the sea ice classification accuracy. This paper proposes a classification model based on deep learning and spectral-spatial-joint features for sea ice images. In the proposed method, by combining a spot of labeled samples with a large number of unlabeled samples, we fully exploit the spectral and spatial information in the hyperspectral remote sensing sea ice data and improve the accuracy of sea ice classification. Compared with the classification method based on single information and other spectral-spatial information, the proposed method effectively extracted sea ice spectral-spatial features with few training samples by using a large amount of unlabeled sample information, and reached the superior overall classification results, which provided a new idea for the classification of remote sensing sea ice images.
(1) Comparing the 1D-CNN model, which can only extract spectral features, and the 2D-CNN model, which can only extract spatial features, the 3D-CNN model can simultaneously extract the spectral and spatial features, and fully exploit the sea ice characteristic information hidden in the remote sensing data. The 3D-CNN model is a classification model suitable for hyperspectral remote sensing sea ice images.
(2) Because the textural characteristics of different types of sea ice are clearly different, texture feature enhancement by GLCM is more conducive for sea ice identification and classification. The proposed method extracts sea ice texture features based on GLCM and combines the texture information with sea ice spectral-spatial information. At the same time, it uses the large-scale features of neighboring unlabeled samples to further enhance the quality of labeled samples. Additionally, the 3D-CNN model is designed for deep spatial spectral feature extraction and classification, which can significantly improve the accuracy of sea ice classification under small sample conditions.
(3) The addition of a large amount of unlabeled sample information increases the computational cost. To reduce the time complexity of the model, the proposed method preprocesses the spectral-spatial information of unlabeled samples. In terms of spectral information, the band selection algorithm is used for dimensionality reduction, a large number of redundant spectral bands are eliminated, and deep spectral feature extraction is performed by using selected bands with a large amount of information and a low similarity. In terms of spatial information, low-correlation texture features are selected based on correlation analysis for deep spatial feature extraction, which effectively reduces the training time. However, the computational cost of the proposed method is relatively high when the experimental area is large.
There is no cloud and snow cover in both data sets in this paper, so we did not discuss this issue. However, cloud cover is an important problem in sea ice detection [
39]. It will bring about the problem of homology (i.e., different things with the same spectrum) in sea ice detection, and affect the improvement of sea ice classification accuracy. Moreover, because snow cover has a different reflectance with sea ice, we can make full use of hyperspectral data with nano-scale spectral resolution to distinguish the snow cover. In addition, melt ponds have an enormous impact on lowering the ice cover albedo, but there are still spectral differences compared to sea ice [
40]. In future research, we intend to integrate microwave remote sensing and higher resolution data to reduce the impact of cloud cover, snow cover, and melt ponds on sea ice detection. In addition, because of the great potential of deep learning in automatic feature extraction and learning model building, it is widely used in various fields [
41]. However, it requires large datasets and long training time. How to balance the sample size and training time is the key for the application. The proposed method can provide a new way of thinking for the application, with small labeled samples.