1. Introduction
The coastal areas constitute one of the most productive yet vulnerable ecosystems in the world [
1]. Furthermore, most of the world population is concentrated in the coastal area, with up to 60% living close to the sea [
2,
3]. As a consequence, coastline monitoring must be an essential issue for public policies regarding coastal management.
The coastal zone is a very dynamic environment affected by different factors, such as hydrography, geology, climate, and vegetation [
4]. The increasing development of coastal areas causes persistent erosion and flooding problems [
5]. Therefore, the knowledge and assessment of the shifts in shoreline position are crucial in the understanding of the morphodynamic processes driving changes [
6]. Thus, coastal observation is under permanent development to improve measuring capabilities and to characterize processes related to water quality, hydrodynamics, meteorology, and ecology, as well as submarine geomophology [
7].
During the last decades, the most commonly used methods for coastline mapping were field surveys [
8,
9] and aerial photography [
10,
11]. Although aerial photographs provide good spatial coverage of the coast [
12], temporal coverage can be restricted [
13]. To avoid such limitations, remote sensing techniques constitute a good alternative due to the increase in the availability of satellite images; the improvement in spatial, temporal, and radiometric resolution on satellite sensors; and the development of tools for geographic data analysis (Geographic Information Systems (GIS)) as well as of image processing techniques [
14]. During the last 30 years, images from different types of satellites have been used to detect coastline, such as radar images, e.g., Synthetic Aperture Radar (SAR) from European Remote Sensing satellite (ERS-1) [
15] and ERS-2 [
16], high spatial resolution (between 0.5 m and 2.5 m) in multispectral images from DubaiSat-1 and DubaiSat-2 satellites [
17], WorldView-2 satellite images [
18], and moderate spatial resolution in multispectral images (Operational Land Imager) from satellite Landsat 8 [
19].
The Landsat project is one of the most frequently used sources of space-based imagery for Earth studies due to the large collection of multispectral imaging of moderate spatial and temporal resolution; in addition, it is a free access database since 2008 [
20]. Therefore, it has been widely used in different areas such as agriculture [
21], forestry [
22,
23], disaster prevention [
24], hydrology [
25], land planning [
26,
27], etc. Nowadays, there are two satellites still in orbit, Landsat 7 and Landsat 8.
Many researchers such as Zhu [
28], Rasuly et al. [
29], Zhang et al. [
30], and Rokni et al. [
31] have been using Landsat images to detect and monitor the coastline using visible and infrared multispectral bands. Although the Landsat project allows to develop long-term (between 10 and 30 years) analyses due to the large image collection [
29,
32,
33], an important limitation in some cases is the spatial resolution. Landsat images permit a coarse pixel analysis, which in some cases is not detailed enough to detect small or sub-pixel features or changes [
34]. In these circumstances, a sub-pixel methodology by super resolution techniques may be useful [
35], such as interpolation techniques [
36,
37]. Most of the accepted interpolation methods for image spatial resolution improvement are based on nearest neighbor and bilinear and bicubic interpolation [
38,
39,
40].
Different types of image processing techniques have been developed for coastline detection, such as segmentation and single band threshold [
41,
42]; segmentation based on local spectral histogram and level set method [
43], which is based on active contours or snakes [
44,
45]; water indexes [
46,
47]; classification techniques such as neural network, isodata, support vector machine among others [
48,
49,
50]; fuzzy logic [
51]; band ratio [
52]; high water-line visual interpretation [
53,
54,
55,
56]; and edge detection [
57]. Some of these techniques are made by manual detection [
43], and others allow an automatic image processing, which is often required in cases like classification of surface water to mask water pixels and in enabling effective monitoring [
58]. This is essential when long-term studies are conducted because automating the process reduces human errors since it requires minimal or no human intervention and improves the standardization and efficiency of the studies.
Deltas are among the most environmentally dynamic ecosystems in the world [
59]. They are also one the most affected coastal environments due to natural resources and human influence [
60]. The deltaic coastal areas are used nowadays as human settlements and for different activities such as tourism, natural reserves, and agriculture, among other things, making this area of high ecological, economic, and social importance [
61]. Hence, one of the main concerns of these areas is related to the impact of the sea level rise driven by climate change [
62], which results, among other things, in coastline retreat. For this reason, it is essential to track coastline changes to understand the relationship between spatiotemporal patterns of sea-level rise and those of coastline changes which requires studying the coastline dynamic at large spatial scales and over long time periods [
63].
It is clear that long-term studies are necessary to better understand coastal changes, so automated methodologies are essential to carry out this task. Also, in some cases, the unsupervised classification methods are useful due to their flexibility [
64] where there is no need to feed the algorithm with prior ground information [
65], which is time consuming and can induce higher human errors. The proposed water indexes combined with the methodology followed gave outstanding results in coastline detection from different sites with different land covers. Also, it showed the effectiveness in detecting a greater quantity of shorelines from different Landsat sensors in different coastal areas compared to the usual indexes used over all the images analyzed in this paper, with a high positional accuracy in the coastlines detected. The methodology proposed has the advantage to be simple, with relatively high accuracy and low-cost implementation.
This research proposes a methodology to automatically extract the coastline from different satellite images by the combination of different processing techniques commonly used in the literature. The methodology includes a new water spectral index, which improves the effectiveness to detect the coastline compared to three of the existing and most common water indexes used: the modified normalized difference water index (MNDWI), the normalized water index (NDWI), and the automated water extraction index (AWEI). The methodology was applied to different deltas located on the Spanish Medierranean coast (Guadalfeo, Adra, and Ebro). Multispectral satellite images from three different sensor, i.e., the thematic mapper (TM), the enhanced thematic mapper plus (ETM+), and the operational land imager (OLI) of the Landsat project were used, which increased their spatial resolution by bicubic interpolation in order to asses a simple sub-pixel analysis. Accuracy assessment was done by comparing the coastline extracted to high resolution data.
5. New Water Index Definition
Water indexes have been widely used to separate water from other features of satellite images. The spectral water indexes method consists of calculating a ratio, pixel by pixel, from different bands on an image to distinguish water from land. Some water indexes are not obtained by ratios but by just applying an arithmetic operations like sum, subtraction, and multiplication as proposed by Feyisa et al. [
87] and Fisher et al. [
58]. Some water indexes developed and the multi-band-based methodology found in the literature [
58,
88] are listed in
Table A3.
The most common spectral water indexes used to extract coastline from satellite images are based on normalized difference indexes used in prior vegetation studies such as the Normalized Difference Vegetation Index (NDVI) and the Normalized Difference Water Index (NDWI) [
89]. One of the most often water index used is the NDWI proposed by McFeeters [
90] to delineate open water features, which uses the top-of-atmosphere (TOA) reflectance of green and NIR bands. Since water features extracted using this NDWI include false positives from built-up land [
31], a Modified Normalized Difference Water Index (MNDWI) was proposed by Xu [
91], using the SWIR1 instead of the NIR band and enhancing the removal of shadows in city areas [
92]. Another water index commonly used is the Automated Water Extraction Index (AWEI) proposed by Feyisa et al. [
87], which has two versions: (1) AWEInsh that was proposed to eliminate non-water pixels, including dark built surfaces in areas with urban background, and (2) AWEIsh that removes shadow pixels that AWEInsh may not effectively eliminate.
In this work, two new water indexes are proposed to identify the coastline based on the assumption that a spectral reflectance signature of water bodies is quite different from that of vegetation and soils. According to Chuvieco [
93], water reflectance is higher in the VIS region and decreases when increasing the wavelengths, which means that water reflectance approaches zero in the NIR and SWIR regions in contrast to soil and vegetation of which reflectance increases significantly.
In this research, the spectral signatures of different land covers were analyzed from selected images of the Guadalfeo, Adra, and Ebro river deltas (
Figure 3,
Figure 4 and
Figure 5). These spectral signatures allow to compare the land cover spectral behavior of the different sensors for each band. It was observed that the highest water reflectance was attained in the blue band, followed by the green one. However, the lowest water reflectance was found on the SWIR 2 band for all sensors. Thus, the proposed indexes were as follows:
where
,
, and
represent the surface reflectance in the green, blue, and shortwave infrared 2 bands, respectively.
The spectral signature of the different land covers from the three deltas tested is quite similar in terms of blue and SWIR2 band spectral behavior. From
Figure 3,
Figure 4 and
Figure 5, it is noticeable that changes in the spectral behavior of the sand beach is almost imperceptible. Usually, NDWI and MNDWI are based on the assumption that spectral behavior of non-water covers have similar behavior in the green band but opposite in the NIR or SWIR1 bands. Although they usually give negative index values for non-water pixels and positive index values for water pixels, this is not always the case, as can be seen in different images analyzed as the TM image from Guadalfeo Delta river (
Figure 3c), the TM and ETM+ image from Adra delta river (
Figure 4b,c, as well as the TM image from Ebro delta river (
Figure 5c), in which, if MNDWI was calculated, sand pixels would take positive values just as water. This can result in sand pixels misinterpreted as water pixels, so the accuracy of the coastline detection decreases. The presence of sand is an important issue because sand reflectance may vary depending on sand color or grain size of sediments and the content of water, as Drakopoulos et al. [
94] confirmed by laboratories measurements.
On the other hand, as can been seen in all the spectral signatures from the three deltas tested, if WI1 and WI2 are calculated in any of the images of
Figure 3,
Figure 4 and
Figure 5, they will usually get positive pixels values but non-water pixels will get values close to zero or negative while water pixel values will be much higher. Thus, these differences in pixel values would help the Otsu’s algorithm performs better in segmentation processes since this method maximizes the between-class variance and minimizes the within-class variance [
95].
5.1. Preprocessing Phase
The preprocessing process was done using open source Quantum GIS (QGIS) software. The Semi Classification Plugin (SCP) allows not only for the semi automatic classification of remote-sensing images but also for the preprocessing of images and raster calculations [
96]. Using SCP, digital numbers of each Landsat image selected were converted into radiance and then into surface reflectance by applying the Dark Object Subtraction (DOS) method [
97]. Prior studies have compared the DOS method to other atmospheric correction models over water areas and urban coastal environments, showing that DOS exhibits better performance, being one of the atmospheric correction models widely used in coastal studies [
7,
29,
31,
98]. Surface reflectance was used rather than TOA reflectance since atmospheric correction is needed for analyzing multiple images acquired from different satellite sensors [
99,
100]. Parameters required for preprocessing were extracted from metadata files downloaded with image data products. To find out more about how the radiometric normalization and the atmospheric correction was calculated, see
Appendix B.
5.2. Processing Phase
The processing step was made using Matlab®. First, each band image was subset to extract the study area in the first part of the automatic algorithm developed; this part allows to select all the original size Landsat images needed from the same zone. When all the images are loaded, the algorithm asks for the desired area to be cropped in the first image. The algorithm user points out the desired area, and the algorithm saves the coordinates selected in the image and applies the crop to the rest of the images with the same parameters. The next step was to apply a Matlab built-in function of unsharp masking (i.e., an image sharpening subtracting a blurred version of the image from itself [
101]) to enhance the edges presented in the images [
102]. Then, the water indexes were applied according to Equations (
1) and (
2) for the proposed water index (WI1 and WI2, respectively), and the expressions found in
Table A3 for the water indexes were selected to compare the proposed ones (NDWI, MNDWI, and AWEI). After the application of the water indexes, the segmentation step was performed to produce a binary image by threshold technique. In segmentation techniques, an image is partitioned into meaningful parts, which have similar features and properties [
103]. This method permits to extract objects by selecting a specific threshold to differentiate the object from the background. Otsu’s method [
104] was selected as the global threshold automatic selection method because it is widely used [
105] and it is one of the best threshold methods of general real-world images with regard to uniformity and shape measures [
95]. Otsu’s method assumes that the image has two kind of pixels that either fall in a foreground class or background class, so iterations are made until an optimal threshold value that separates both classes is found.
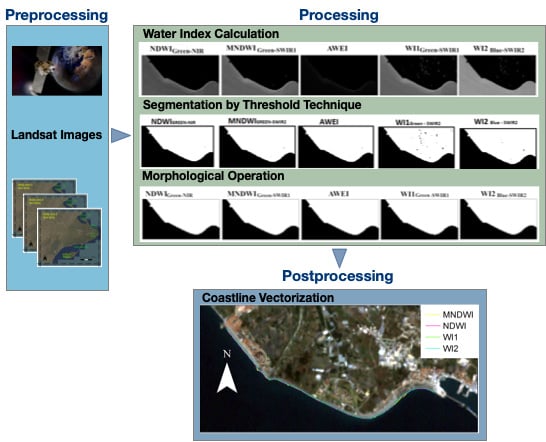
Once a binarized image is obtained, a morphological operation is applied to clean up the image, removing useless pixels. The morphological operation was an imfill built-in Matlab function to fill all the holes inside the land area. Finally, a vectorization step was performed to obtain the coordinates of the coastline extracted. An example of the sequence of the methodology applied on every image can be seen in
Figure 6 from an image obtained in the Guadalfeo delta on September 12, 2013 by the OLI sensor.
This methodology was applied to original-size Landsat images and to increased spatial resolution images for further assessment of accuracy improvement. We used bicubic interpolation because it offers the best results compared to different linear up-sampling methods [
37,
39,
106,
107] in spite of its simplicity [
108,
109].
The spatial resolution increase was assessed by detecting the coastline with the original spatial resolution image (30 m/pixel) and then by testing bicubic interpolation with different factors of up-sampling to assess if the accuracy of the detected coastline with WI1 and WI2 could improve. We assessed bicubic interpolation with factors of 2 (15 m/pixel), 3 (10 m/pixel), 5 (6 m/pixel), and 10 (3 m/pixel).
5.3. Data Validation
The methodology proposed was applied using NDWI, MNDWI, and AWEI indexes and then compared to the coastline extracted with the new water indexes proposed WI1 and WI2. The statistic metric used to analyze the goodness of the different indexes were the mean and the standard deviation of the distances between the shoreline extracted from high-resolution data and from the Landsat images. It was calculated as follows:
where
Dj = Distance in meters between the high resolution data and the data derived from the Landsat images. The difference of the vertical distance between the shorelines compared for the same X coordinate was calculated. Dj is a positive value as Landsat data is seaward, and if Dj is a negative value, it means that the Landsat data is landward.
Yj_LS = Coordinate of the Landsat data.
Yj_Hr = Coordinate of the high-resolution data.
Mean = The mean of Dj in meters.
STD = Standard deviation of Dj in meters.
n = Number of elements of the data evaluated.
8. Conclusions
The main goal of this research was to detect the coastline automatically from Landsat satellite images. Although this methodology has been applied to three Spanish Mediterranean deltas (Guadalfeo, Adra, and Ebro) to assess the method performance, the study of the morphology of the delta is beyond the scope of this paper.
The methodology is based on the definition of a new water index that improves the effectiveness of coastline detection from different coastal areas over the common water indexes that are used in the literature, namely, NDWI, MNDWI, and AWEI. This new index uses the blue and SWIR 2 bands of Landsat images. The methodology with the new index was applied to images from three different sensors TM, ETM+, and OLI of the Landsat project. In addition, a sub-pixel approximation was performed by applying bicubic interpolation.
The methodology permits the extraction of shorelines from as many images as are required to obtain outstanding results compared to that of the most commonly used water indexes for coastline detection. The water indexes that are most commonly used currently in the literature to detect water have been separately shown in this paper to be less useful than was expected for each of the different sites. However, the method with water index WI2 showed high performance by detecting the coastline in more than 96% of the satellite images that were analyzed. In addition, this WI2 method allows for the shoreline to be detected from different Landsat sensors and different sites with micro-tidal conditions and diverse land cover, such as build-up, agriculture, greenhouses, or wetlands, with good positional accuracy. This provides a great advantage because the same method can be used in different kinds of coastal areas unlike other water indexes that are usually restricted to certain sites.
Bicubic interpolation was unable to enhance the accuracy of the extracted shoreline, so it is advisable to assess more complex techniques and to verify whether better accuracy is possible.
Further investigation could be carried out in future work in order to do the following:
Evaluate the influence of different site conditions (sea level rise, tide effects, run-up, etc.) with the accuracy that is obtained with the methodology proposed.
Use other satellite images with similar characteristics but with higher spatial resolution (10 m–20 m) such as Sentinel 2 imagery from the European Space Agency (ESA) to assess their performance.
Test other sup-pixel approaches to improve the accuracy, such as the super resolution technique based on Fourier transform, discrete wavelet transform [
114], and Daubechies complex wavelet transform [
115], which are frequency domain techniques for image enhancement.