MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products
Abstract
:1. Introduction
2. MODIS L1B Calibration Algorithm
3. Detector Gain
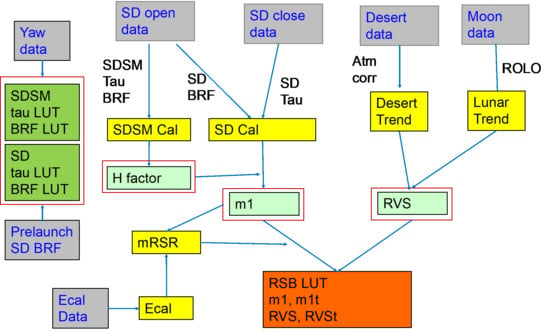
4. Method
4.1. SDSM Calibration
4.1.1. Detector Gain: m1
4.1.2. m1 Time Series
4.2. RVS
4.2.1. Desert Trend
4.2.2. Lunar Trend
4.2.3. RVS Characterization
4.3. Relative Spectral Response (RSR) Modulation
5. Results
5.1. OBPG RSB Calibration LUT
5.2. Artifact Mitigation
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Glossary
| Acronyms | Definition |
| 6SV | Atmospheric correction model. https://6s.ltdri.org/ |
| BOS | Beginning of the Scan |
| BRDF | Bidirectional Reflectance Distribution Function |
| BRF | Bidirectional Reflectance Function |
| Ecal | Electronic self Calibration |
| EOS | End of the Scan |
| H factor | Relative SD reflectivity |
| L1A | Formatted raw instrument data |
| L1B | Calibrated radiance computed from L1A |
| L2 | Derived per-pixel ocean color products L1B |
| L3 | Global binned ocean color products from L2 |
| LUT | Look-Up-Table |
| M1 | Detector radiometric gain coefficient |
| M1t | Time stamp of m1 |
| M11 | OBPG cross-calibration RVS correction coefficient |
| MCST | MODIS Calibration Support Team |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MODISA | MODIS Aqua |
| MODIST | MODIS Terra |
| mRSR | Moduated RSR |
| NIR | Near-InfraRed |
| OBPG | Ocean Biological Processing Group |
| R2014 | https://oceancolor.qsfc.nasa.gov/reprocessing/r2014/aqua/ |
| R2018 | https://oceancolor.qsfc.nasa.gov/reprocessing/r2018/aqua/ |
| ROLO | RObotic Lunar Observatory |
| RSB | Reflective Solar Bands |
| RSR | Reflective Spectral Response |
| Rrs | Remote sensing reflectance |
| RVS | Response Versus Scan angle |
| RVSt | Time stamp of RVS |
| SAA | Solar Attanuation screen Assembly |
| SD | Solar Diffuser |
| SDSM | Solar Diffuser Stability Monitor |
| SIS | Spectral Integrating Sphere |
| SNR | Signal to Noise Ratio |
| SV | Space View |
| Tau | Screen transmission functions |
| TOA | Top of Atmosphere |
References
- Xiong, X.; Barnes, W.L.; Chiang, K.; Erives, H.; Che, N.; Sun, J.; Isaacman, A.T.; Salomonson, V.V. Status of Aqua MODIS on-orbit calibration and characterization. In Proceedings of the Sensors, Systems, and Next-Generation Satellites VIII, Maspalomas, Spain, 13–15 September 2004. [Google Scholar]
- Franz, B.A.; Kwiatowska, E.J.; Meister, G.; McClain, C.R. Moderate Resolution Imaging Spectroradiometer on Terra: Limitations for ocean color applications. J. Appl. Remote. Sens. 2008, 2, 23525. [Google Scholar] [CrossRef]
- Meister, G.; Eplee, R.E.; Franz, B.A. Corrections to MODIS Terra calibration and polarization trending derived from ocean color products. In Proceedings of the Earth Observing Systems XIX, San Diego, CA, USA, 18–20 August 2014. [Google Scholar]
- Meister, G.; Franz, B.A. Corrections to the MODIS Aqua Calibration Derived from MODIS Aqua Ocean Color Products. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 6534–6541. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Werdell, P.J.; McClain, C.R. Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 2007, 46, 5068–5082. [Google Scholar] [CrossRef] [PubMed]
- Franz, B.A. Status of MODIS and VIIRS OC & SST Production & Distribution. In Proceedings of the MODIS/VIIRS Science Team Meeting, Silver Spring, MD, USA, 6–10 June 2016. [Google Scholar]
- Turpie, K.R.; Eplee, R.E.; Franz, B.A.; Del Castillo, C. Calibration uncertainty in ocean color satellite sensors and trends in long-term environmental records. SPIE Sens. Technol. Appl. 2014, 9111, 911103. [Google Scholar]
- Franz, B.A.; Bailey, S.W.; Meister, G.; Werdell, P.J. Consistency of the NASA Ocean Color Data Record. In Proceedings of the Ocean Optics 2012, Glasgow, UK, 8–12 October 2012. [Google Scholar]
- International Ocean-Colour Coordinating Group. In-Flight Calibration of Satellite Ocean-Colour Sensors; Report Number 14; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2013. [Google Scholar]
- MODIS Characterization and Calibration Team. MODIS Instrument Operations Status. In Proceedings of the MODIS/VIIRS Science Team Meeting, Silver Spring, MD, USA, 15–19 October 2018. [Google Scholar]
- Sun, J.; Angal, A.; Chen, H.; Geng, X.; Wu, A.; Choi, T.; Chu, M. MODIS reflective solar bands calibration improvements in Collection 6. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization II, Bertinoro, Italy, 25–28 June 2012. [Google Scholar]
- Lee, S.; Meister, G. MODIS Aqua Optical Throughput Degradation Impact on Relative Spectral Response and Calibration of Ocean Color Products. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5214–5219. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.-Q.; Esposito, J.A.; Guenther, B.; Barnes, W.L. MODIS reflective solar bands calibration algorithm and on-orbit performance. In Proceedings of the Optical Remote Sensing of the Atmosphere and Clouds III, Québec City, QC, Canada, 3–6 February 2003. [Google Scholar]
- Lee, S.; Meister, G. MODIS solar diffuser degradation determination and its spectral dependency. In Proceedings of the Earth Observing Systems XXIII, San Diego, CA, USA, 21–23 August 2018. [Google Scholar]
- Meister, G.; Pan, C.; Patt, F.S.; Franz, B.; Xiong, J.; McClain, C.R. Correction of subframe striping in high-resolution MODIS ocean color products. In Proceedings of the Earth Observing Systems XII, San Diego, CA, USA, 10–14 August 2007. [Google Scholar]
- MODIS Characterization Support Team. Available online: https://mcst.gsfc.nasa.gov/ (accessed on 12 September 2019).
- Sun, J.; Xiong, X.; Angal, A.; Chen, H.; Wu, A.; Geng, X. Time-Dependent Response Versus Scan Anglefor MODIS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3159–3174. [Google Scholar] [CrossRef]
- Xiong, X.; Salomonson, V.V.; Chiang, K.-F.; Wu, A.; Guenther, B.W.; Barnes, W. On-orbit characterization of RVS for MODIS thermal emissive bands. In Proceedings of the Passive Optical Remote Sensing of the Atmosphere and Clouds IV, Honolulu, Hi, USA, 9–10 November 2004. [Google Scholar]
- Xiong, X.; Geng, X.; Angal, A.; Sun, J.; Barnes, W. Using the Moon to track MODIS reflective solar bands calibration stability. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XV, Prague, Czech Republic, 19–22 September 2011. [Google Scholar]
- Helder, D.L.; Basnet, B.; Morstad, D.L. Optimized identification of worldwide radiometric pseudo-invariant calibration sites. Can. J. Remote. Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Kieffer, H.H. Photometric Stability of the Lunar Surface. Icarus 1997, 130, 323–327. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Stone, T.C. The Spectral Irradiance of the Moon. Astron. J. 2005, 129, 2887–2901. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.-Q.; Xiong, X.; Barnes, W.L.; Guenther, B. MODIS Reflective Solar Bands On-Orbit Lunar Calibration. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 2383–2393. [Google Scholar] [CrossRef]
- Bailey, S.W. On-orbit calibration of the Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite for ocean color applications. Appl. Opt. 2015, 54, 1984. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Eplee, R.E., Jr.; Lee, S.; Patt, F.S.; Proctor, C.; Meister, G. NASA Multi-Mission Ocean Color Reprocessing 2018. In Proceedings of the Ocean Optics XXIV, Dubrovnik, Croatia, 8–12 October 2018; Available online: https://www.researchgate.net/publication/331652881_NASA_Multi-Mission_Ocean_Color_Reprocessing_20180 (accessed on 12 September 2019).



















| SDSM | Wavelength | Land/Atmosphere | Center Wavalength (nm) | Band Width (nm) | Ocean | Center Wanalength | Band Width (nm) |
|---|---|---|---|---|---|---|---|
| Detector 1 | 412 | Band 1 | 645 | 50 | Band 8 | 412 | 15 |
| Detector 2 | 466 | Band 2 | 859 | 35 | Band 9 | 443 | 10 |
| Detector 3 | 530 | Band 3 | 469 | 20 | Band 10 | 488 | 10 |
| Detector 4 | 554 | Band 4 | 555 | 20 | Band 11 | 531 | 10 |
| Detector 5 | 646 | Band 5 | 1240 | 20 | Band 12 | 551 | 10 |
| Detector 6 | 747 | Band 6 | 1640 | 24 | Band 13 | 667 | 10 |
| Detector 7 | 857 | Band 7 | 2130 | 50 | Band 14 | 678 | 10 |
| Detector 8 | 904 | Band 17 | 905 | 30 | Band 15 | 748 | 10 |
| Detector 9 | 936 | Band 18 | 936 | 10 | Band 16 | 869 | 10 |
| Band 19 | 940 | 50 | |||||
| Band 26 | 1375 | 30 |
| Bands | Calibration Targets | RVS Characterization |
|---|---|---|
| Bands 1–9 Bands 17–19 Bans 26 | Moon, SD, desert | 2nd order polynomial |
| Bands 10–16 | Moon, SD | 2nd order polynomial |
| R2014 * | R2018 | |
|---|---|---|
| SDSM calibration | Detector 9 normalization Sd/SDSM screen for detector 9 degradation | Detector 9 normalization refined by SD/SDSM screen SDSM wavelength model for interpolation and detector 9 degradation |
| SD calibration | Use highest SD unsaturated signal to maximize SNR | Use low SD signal for all bands to better match ocean radiance |
| Temporal RVS characterization | 2nd to 4th order fit Remove BRDF effect by fitting observed data vs. view and illumination geometric | 2nd order fit for all bands Use atmospheric correction to remove BRDF effect Apply modulated RSR impact |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Meister, G.; Franz, B. MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products. Remote Sens. 2019, 11, 2187. https://doi.org/10.3390/rs11192187
Lee S, Meister G, Franz B. MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products. Remote Sensing. 2019; 11(19):2187. https://doi.org/10.3390/rs11192187
Chicago/Turabian StyleLee, Shihyan, Gerhard Meister, and Bryan Franz. 2019. "MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products" Remote Sensing 11, no. 19: 2187. https://doi.org/10.3390/rs11192187
APA StyleLee, S., Meister, G., & Franz, B. (2019). MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products. Remote Sensing, 11(19), 2187. https://doi.org/10.3390/rs11192187