Estimating Fine-Scale Heat Vulnerability in Beijing Through Two Approaches: Spatial Patterns, Similarities, and Divergence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.2.1. Land Surface Temperature and Normalized Difference Vegetation Index
2.2.2. Jiedao Socioeconomic Conditions
2.3. Heat Vulnerability Index
2.4. Analytic Methods
3. Results
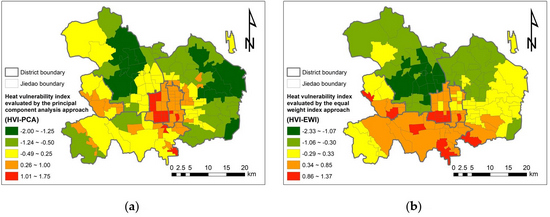
3.1. Spatial Pattern of Heat Vulnerability in Beijing
3.2. Comparing PCA and EWI
4. Discussion
4.1. Spatial Patterns, Similarities, and Divergence of Heat Vulnerability in Beijing
4.2. Reasons for Differences between the PCA Approach and the EWI Approach
4.3. Limitations of This Study
4.4. The Implications for Future Research and Urban Planning
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guijie, L. Heat Wave Impact on Mortality in Beijing in 2010. J. Environ. Hyg. 2015, 5, 525–529. [Google Scholar]
- Ya, L. Impacts of heat waves on emergency department visits in Beijing, 2010. South. China J. Prev. Med. 2014, 40, 322–326. [Google Scholar]
- Simmonds, I. What causes extreme hot days in Europe? Environ. Res. Lett. 2018, 13, 071001. [Google Scholar] [CrossRef]
- Fouillet, A. Excess mortality related to the August 2003 heat wave in France. Int. Arch. Occup. Environ. Health 2006, 80, 16–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, G.B.; Bell, M.L. Heat waves in the United States: Mortality risk during heat waves and effect modification by heat wave characteristics in 43 US communities. Environ. Health Perspect. 2010, 119, 210–218. [Google Scholar] [CrossRef]
- Rosenthal, K. Evaluating the Impact of the Urban Heat Island on Public Health: Spatial and Social Determinants of Heat-Related Mortality in New York City. Ph.D. Thesis, Columbia University, New York, NY, USA, 2010. [Google Scholar]
- Tan, J. The urban heat island and its impact on heat waves and human health in Shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef]
- Ma, Q. Quantifying spatiotemporal patterns of urban impervious surfaces in China: An improved assessment using nighttime light data. Landsc. Urban. Plan. 2014, 130, 36–49. [Google Scholar] [CrossRef]
- Wu, J.; Xiang, W.-N.; Zhao, J. Urban ecology in China: Historical developments and future directions. Landsc. Urban. Plan. 2014, 125, 222–233. [Google Scholar] [CrossRef]
- Simmonds, I.; Keay, K. Weekly cycle of meteorological variations in Melbourne and the role of pollution and anthropogenic heat release. Atmos. Environ. 1997, 31, 1589–1603. [Google Scholar] [CrossRef]
- Huang, G.; Zhou, W.; Cadenasso, M.L. Is everyone hot in the city? Spatial pattern of land surface temperatures, land cover and neighborhood socioeconomic characteristics in Baltimore, MD. J. Environ. Manag. 2011, 92, 1753–1759. [Google Scholar] [CrossRef]
- Aminipouri, M.; Knudby, A.; Ho, H.C. Using multiple disparate data sources to map heat vulnerability: Vancouver case study. Can. Geogr. Geogr. Can. 2016, 60, 356–368. [Google Scholar] [CrossRef]
- Reid, C.E. Mapping community determinants of heat vulnerability. Environ. Health Perspect. 2009, 117, 1730–1736. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.P. Developing an applied extreme heat vulnerability index utilizing socioeconomic and environmental data. Appl. Geogr. 2012, 35, 23–31. [Google Scholar] [CrossRef]
- Reid, C.E. Evaluation of a heat vulnerability index on abnormally hot days: An environmental public health tracking study. Environ. Health Perspect. 2012, 120, 715–720. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Woodward, A. ; Cirendunzhu; Liu, Q.Y. County-level heat vulnerability of urban and rural residents in Tibet, China. Environ. Health 2016, 15, 3. [Google Scholar] [CrossRef] [PubMed]
- Harlan, S.L. Neighborhood microclimates and vulnerability to heat stress. Soc. Sci. Med. 2006, 63, 2847–2863. [Google Scholar] [CrossRef] [PubMed]
- Harlan, S.L. Neighborhood effects on heat deaths: Social and environmental predictors of vulnerability in Maricopa County, Arizona. Environ. Health Perspect. 2013, 121, 197–204. [Google Scholar] [CrossRef]
- Inostroza, L.; Palme, M.; de la Barrera, F. A Heat Vulnerability Index: Spatial Patterns of Exposure, Sensitivity and Adaptive Capacity for Santiago de Chile. PLoS ONE 2016, 11, 26. [Google Scholar] [CrossRef]
- Azhar, G. Heat Wave Vulnerability Mapping for India. Int. J. Environ. Res. Public Health 2017, 14, 10. [Google Scholar] [CrossRef]
- Jenerette, G.D. Micro-scale urban surface temperatures are related to land-cover features and residential heat related health impacts in Phoenix, AZ USA. Landsc. Ecol. 2016, 31, 745–760. [Google Scholar] [CrossRef]
- Yichen, W. Research on Urban Heat Wave Vulnerability Assessment under Climate Change; Beijing University of Civil Engineering and Architecture: Beijing, China, 2015. [Google Scholar]
- Xuemei, Z. Comparison of heat wave vulnerability between coastal and inland cities of Fujian Province in the past 20 years. Prog. Geogr. 2016, 35, 1197–1205. [Google Scholar]
- Pan, X. Incorporating social vulnerability to assess population health risk due to heat stress in China. Acta Geogr. Sin. 2015, 70, 1041–1051. [Google Scholar]
- Zhang, W.; Zheng, C.; Chen, F. Mapping heat-related health risks of elderly citizens in mountainous area: A case study of Chongqing, China. Sci. Total Environ. 2019, 663, 852–866. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Wilhelmi, O.V.; Uejio, C. Assessment of heat exposure in cities: Combining the dynamics of temperature and population. Sci. Total Environ. 2019, 655, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Sankoh, O.; Tatem, A.J. Mapping the environmental and socioeconomic coverage of the INDEPTH international health and demographic surveillance system network. Health Place 2015, 36, 88–96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rhew, I.C. Validation of the normalized difference vegetation index as a measure of neighborhood greenness. Ann. Epidemiol. 2011, 21, 946–952. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote. Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Tu, X.; Huang, G.; Wu, J. Contrary to common observations in the west, urban park access is only weakly related to neighborhood socioeconomic conditions in Beijing, China. Sustainability 2018, 10, 1115. [Google Scholar] [CrossRef]
- Balbus, J.M.; Malina, C. Identifying vulnerable subpopulations for climate change health effects in the United States. J. Occup. Environ. Med. 2009, 51, 33–37. [Google Scholar] [CrossRef]
- Jenerette, G.D. Ecosystem services and urban heat riskscape moderation: Water, green spaces, and social inequality in Phoenix, USA. Ecol. Appl. 2011, 21, 2637–2651. [Google Scholar] [CrossRef] [PubMed]
- Ming-shun, Z.; Yi-chen, W. Research on Evaluation System of Heat Wave Vulnerability in Beijing City. Urban. Environ. Stud. 2015, 1, 16–33. [Google Scholar]
- Räsänen, A. Zoning and weighting in urban heat island vulnerability and risk mapping in Helsinki, Finland. Reg. Environ. Chang. 2019, 19, 1481–1493. [Google Scholar] [CrossRef] [Green Version]
- Wiréhn, L.; Danielsson, Å.; Neset, T.-S.S. Assessment of composite index methods for agricultural vulnerability to climate change. J. Environ. Manag. 2015, 156, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Reckien, D. What is in an index? Construction method, data metric, and weighting scheme determine the outcome of composite social vulnerability indices in New York City. Reg. Environ. Chang. 2018, 18, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wolf, T.; McGregor, G.; Analitis, A. Performance Assessment of a Heat Wave Vulnerability Index for Greater London, United Kingdom. Weather. Clim. Soc. 2014, 6, 32–46. [Google Scholar] [CrossRef] [Green Version]
- Maier, G. Assessing the Performance of a Vulnerability Index during Oppressive Heat across Georgia, United States. Weather. Clim. Soc. 2014, 6, 253–263. [Google Scholar] [CrossRef]





| Literature | Index | Approach | Principal Component/Factor | Variables |
|---|---|---|---|---|
| Reid et al. [13] | Heat vulnerability index | Principal components analysis (PCA) | Social/environmental vulnerability | Below poverty line |
| Race other than white | ||||
| Less than a high school (HS) diploma | ||||
| No green space | ||||
| Social isolation | Live alone | |||
| Age ≥ 65 living alone | ||||
| Prevalence of no air conditioning (AC) | No central AC | |||
| No AC of any kind | ||||
| Proportion of elderly/diabetes | Diabetes | |||
| Age ≥ 65 years | ||||
| Johnson et al. [14] | Extreme heat vulnerability index | PCA | 1 | Females age 65 and up |
| Males age 65 and up | ||||
| Females age 65 and up living alone | ||||
| White population | ||||
| Females head of household | ||||
| Males age 65 and up living alone | ||||
| Mean family income in 1989 | ||||
| Per capita income in 1989 | ||||
| Mean household income in 1989 | ||||
| Population 25 and older with less than high school education | ||||
| Asian population | ||||
| Population age 65 and older in group living | ||||
| 2 | Other race population | |||
| Hispanic population | ||||
| Population 25 and older with a high school education | ||||
| 3 | Normalized difference built-up index (NDBI) | |||
| Normalized difference vegetation index (NDVI) | ||||
| 4 | Black population | |||
| Land surface temperature (LST) | ||||
| Reid et al. [15] | Heat vulnerability index | PCA | Social/environmental Vulnerability | Below poverty line |
| Race other than white | ||||
| Less than a high school diploma | ||||
| No green space | ||||
| Social isolation | Live alone | |||
| Age ≥ 65 living alone | ||||
| Prevalence of no AC | No central AC | |||
| No AC of any kind | ||||
| Proportion of elderly/diabetes | Diabetes | |||
| Age ≥ 65 years | ||||
| Harlan et al. [18] | Heat vulnerability index | PCA | Socioeconomic vulnerability | Ethnic minority |
| Latino immigrant | ||||
| < Poverty line | ||||
| No HS diploma | ||||
| No central AC/cooler | ||||
| Elderly/isolation | ≥ 65 years of age | |||
| ≥ 65 years of age × living alone | ||||
| Living alone | ||||
| Unvegetated area | Unvegetated area (mean) | |||
| Unvegetated area (SD) | ||||
| Bai et al. [16] | Heat vulnerability index | PCA | Poverty | Low income |
| Low income among seniors | ||||
| Low income households | ||||
| Elderly/fragile health/illiterate | Age ≥ 60 | |||
| Loss of labor ability | ||||
| Illiterate | ||||
| Social isolation | Living alone | |||
| Age ≥ 60 living alone | ||||
| Small dwelling | Households with only one room | |||
| Households ≤ 8 m2 living spaces | ||||
| Zhang et al. [25] | Heat risk index | Crichton’s Risk Triangle (a function of hazard, exposure, and vulnerability) | Hazard index | Daytime temperature |
| Nighttime temperature | ||||
| High temperature days | ||||
| Air quality | ||||
| Exposure index | Elderly population | |||
| Elderly with disability | ||||
| Low income elderly | ||||
| Vulnerability index | Vegetation | |||
| Water bodies | ||||
| Terrain condition | ||||
| Housing condition | ||||
| Traffic convenience | ||||
| Medical facilities | ||||
| Hu et al. [26] | Excessive heat events (EHEs) | Total population exposed to the diurnal heat | Temperature | Near-surface air temperature |
| Population | Commute-adjusted diurnal population |
| Category | Independent Variable | Mean (range) | STD | Data Source |
|---|---|---|---|---|
| Demographic variables | Percentage of population ≥ 65 years of age (≥ 65) | 10.06 (2.13–24.54) | 3.98 | Tabulation on the Population Census of Beijing Municipality (2010) |
| Percentage of population < 5 years of age (< 5) | 3.16 (1.32–5.72) | 0.86 | ||
| Percentage of the population below high school education (below HS) | 35.98 (11.28–77.38) | 12.59 | ||
| Percentage of population with a college education or above (college or above) | 37.23 (4.82–79.63) | 13.76 | ||
| Percentage of illiterate population (illiteracy) | 1.18 (0.32–2.88) | 0.58 | ||
| Percentage of population who live alone (living alone) | 9.36 (3.95–23.50) | 3.60 | ||
| Percentage of unhealthy population over 60 (unhealthy seniors) | 15.51 (12.52–20.23) | 2.96 | ||
| Average income 1 (income) | 29,340.01 (10,278.27–48,459.39) | 8540.04 | ||
| Air conditioners | Number of air conditioners per 100 households (AC) | 0.56 (0.00–1.00) | 0.36 | Beijing Area Statistical Yearbook 2011 |
| Land cover | The mean pixel-level (1 km*1 km) value of normalized difference vegetation index (NDVI) | 0.28 (0.03–0.70) | 0.13 | NDVI from Moderate-resolution imaging spectroradiometer (MODIS 2) data (July 2010) |
| Land surface temperature | The mean of pixel-level (1 km*1 km) land surface temperature (LST) value of each jiedao | 38.33 (32.95–40.77) | 1.18 | LST from MODIS data (July 2010) |
| Range | Assigned Value |
|---|---|
| < −1.25 | −3 |
| −1.25 to −0.75 | −2 |
| −0.75 to −0.25 | −1 |
| −0.25 to 0.25 | 0 |
| 0.25 to 0.75 | 1 |
| 0.75 to 1.25 | 2 |
| > 1.25 | 3 |
| Factor 1: Illiteracy/Unhealthy/AC/Income | Factor 2: LST/NDVI | Factor 3: Living Alone/Below HS/College or Above | Factor 4: <5/≥ 65 | The Absolute Value of the Variable Weight | The Absolute Value of the Normalized Variable Weight | |
|---|---|---|---|---|---|---|
| Illiteracy | 0.387 (0.903) | −0.147 (−0.174) | 0.056 (0.009) | 0.131 (0.02) | 0.427 | 0.119 |
| Unhealthy seniors | 0.286 (0.683) | 0.146 (0.403) | −0.005 (0.108) | 0.122 (0.19) | 0.549 | 0.153 |
| AC | −0.193 (−0.574) | −0.205 (−0.33) | −0.009 (0.056) | 0.188 (0.271) | 0.219 | 0.061 |
| Income | −0.193 (−0.531) | 0.162 (0.407) | −0.055 (0.188) | 0.158 (0.423) | 0.072 | 0.020 |
| LST | −0.043 (−0.009) | 0.486 (0.911) | −0.021 (0.155) | −0.177 (0.008) | 0.245 | 0.068 |
| NDVI | −0.017 (−0.084) | −0.431 (−0.866) | 0.112 (−0.079) | −0.022 (−0.224) | 0.358 | 0.099 |
| Living alone | −0.126 (−0.268) | 0.07 (−0.049) | −0.546 (−0.81) | 0.273 (0.126) | 0.329 | 0.091 |
| Below HS | 0.09 (0.346) | 0.014 (−0.226) | −0.334 (−0.743) | −0.044 (−0.387) | 0.274 | 0.076 |
| College or above | −0.18 (−0.544) | −0.027 (0.146) | 0.352 (0.723) | −0.045 (0.274) | 0.099 | 0.028 |
| < 5 | −0.035 (0.12) | 0.074 (−0.121) | 0.227 (−0.021) | −0.655 (−0.909) | 0.389 | 0.108 |
| ≥ 65 | 0.224 (0.365) | −0.11 (0.125) | 0.166 (0.5) | 0.358 (0.609) | 0.638 | 0.177 |
| Total Variance Explained | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Com-ponent | Initial Eigenvalues | Extraction Sums of Squared Loadings | Rotation Sums of Squared Loadings | ||||||
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | |
| 1 | 3.61 | 32.80 | 32.80 | 3.61 | 32.80 | 32.80 | 2.54 | 23.05 | 23.05 |
| 2 | 2.50 | 22.70 | 55.50 | 2.50 | 22.70 | 55.50 | 2.15 | 19.56 | 42.61 |
| 3 | 1.38 | 12.57 | 68.07 | 1.38 | 12.57 | 68.07 | 2.06 | 18.74 | 61.35 |
| 4 | 1.04 | 9.44 | 77.50 | 1.04 | 9.44 | 77.50 | 1.78 | 16.15 | 77.50 |
| 5 | 0.70 | 6.40 | 83.90 | ||||||
| 6 | 0.52 | 4.71 | 88.62 | ||||||
| 7 | 0.48 | 4.41 | 93.02 | ||||||
| 8 | 0.30 | 2.71 | 95.73 | ||||||
| 9 | 0.24 | 2.17 | 97.90 | ||||||
| 10 | 0.20 | 1.83 | 99.73 | ||||||
| 11 | 0.03 | 0.27 | 100.00 | ||||||
| Indicator | The Absolute Value of the EWI Coefficient | The Absolute Value of the Normalized PCA Coefficient | The Absolute Value of the PCA Coefficient | Percentage of Change |
|---|---|---|---|---|
| Education | 0.111 | 0.222 | 0.800 | 1.001 |
| Population ≥ 65 | 0.111 | 0.177 | 0.638 | 0.595 |
| Unhealthy seniors | 0.111 | 0.153 | 0.549 | 0.373 |
| Population < 5 | 0.111 | 0.108 | 0.389 | −0.027 |
| NDVI | 0.111 | 0.099 | 0.358 | −0.105 |
| Living alone | 0.111 | 0.091 | 0.329 | −0.177 |
| LST | 0.111 | 0.068 | 0.245 | −0.387 |
| AC | 0.111 | 0.061 | 0.219 | −0.452 |
| Income | 0.111 | 0.020 | 0.072 | −0.820 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Huang, G.; Jia, P.; Wu, J. Estimating Fine-Scale Heat Vulnerability in Beijing Through Two Approaches: Spatial Patterns, Similarities, and Divergence. Remote Sens. 2019, 11, 2358. https://doi.org/10.3390/rs11202358
Guo X, Huang G, Jia P, Wu J. Estimating Fine-Scale Heat Vulnerability in Beijing Through Two Approaches: Spatial Patterns, Similarities, and Divergence. Remote Sensing. 2019; 11(20):2358. https://doi.org/10.3390/rs11202358
Chicago/Turabian StyleGuo, Xuan, Ganlin Huang, Peng Jia, and Jianguo Wu. 2019. "Estimating Fine-Scale Heat Vulnerability in Beijing Through Two Approaches: Spatial Patterns, Similarities, and Divergence" Remote Sensing 11, no. 20: 2358. https://doi.org/10.3390/rs11202358
APA StyleGuo, X., Huang, G., Jia, P., & Wu, J. (2019). Estimating Fine-Scale Heat Vulnerability in Beijing Through Two Approaches: Spatial Patterns, Similarities, and Divergence. Remote Sensing, 11(20), 2358. https://doi.org/10.3390/rs11202358