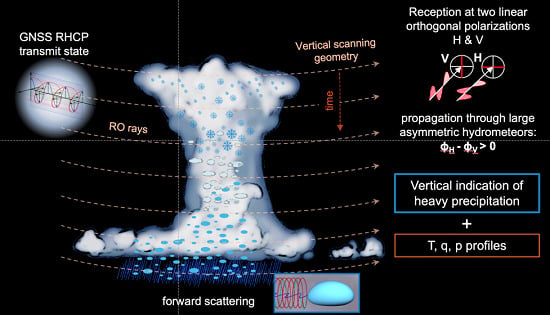
Benefits of a Closely-Spaced Satellite Constellation of Atmospheric Polarimetric Radio Occultation Measurements
Abstract
:1. Introduction
2. RO Measurement Requirements
2.1. Polarimetric RO Concept
2.2. The Cion RO Receiver
3. Results
3.1. Three-Satellite Constellation
3.1.1. Representation of Precipitation at RO Observation Times
3.1.2. Near-Simultaneous RO Inside and Outside of Heavy Precipitation
3.2. Other Orbit Constellation Scenarios
4. Discussion
- Over one year, a 3-satellite constellation 45° inclination plane will collect 400,000 events and 97% of these are complete events (i.e., all three satellites capture a RO from the same GNSS transmitter).
- Of these complete events, the superposition of GPM IMERG data reveals that 15,500 will have at least one observation crossing detectable precipitation and one crossing un-detectable precipitation.
- The 98° orbit resulted in more events meeting the criteria in (2) above than the 45° inclination orbit, because there is more distance separation between the RO observations. However, the relative inclination with the GPS and GLONASS satellites also makes these observations more likely to have α ~90° deg, and hence smaller deff distances. From a scientific standpoint, it is better to have smaller distances to be able to characterize the convection inside and in the nearby environment (too far apart is less desirable). With this rationale, the 98° orbit is less optimal for the study of the immediate surrounding of precipitation.
- Collections of RO observations with α closer to 90° are more perpendicular to each other, but also suffer a larger tangent point drift. In other words, even though deff is small in general for the 45° case, the tangent point drift will be smaller. Therefore, there is less likelihood of a ray path overlap between adjacent RO soundings.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stephens, G.L.; L’Ecuyer, T.; Forbes, R.; Gettlemen, A.; Golaz, J.-C.-C.; Bodas-Salcedo, A.; Suzuki, K.; Gabriel, P.; Haynes, J. Dreary state of precipitation in global models. J. Geophys. Res. 2010, 115, D24211. [Google Scholar] [CrossRef]
- Brown, R.G.; Zhang, C. Variability of mid-tropospheric moisture and its effect on cloud-top height distribution during TOGA COARE. J. Atmos. Sci. 1997, 54, 2760–2774. [Google Scholar] [CrossRef]
- Holloway, C.E.; Neelin, J.D. Moisture vertical structure, column water vapor, and tropical deep convection. J. Atmos. Sci. 2009, 66, 1665–1683. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Wahrlich, R. Observed evolution of tropical deep convective events and their environment. Mon. Weather Rev. 1999, 127, 1777–1795. [Google Scholar] [CrossRef]
- Parsons, D.B.; Redelsperger, J.-L.; Yoneyama, K. The evolution of the tropical Western Pacific atmosphere-ocean system following the arrival of a dry intrusion. Q. J. R. Meteorol. Soc. 2000, 126, 517–548. [Google Scholar] [CrossRef]
- Tompkins, A.M. Organization of Tropical Convection in Low Vertical Wind Shears: The Role of Cold Pools. J. Atmos. Sci. 2001, 58, 1650–1672. [Google Scholar] [CrossRef]
- Redelsperger, J.L.; Parsons, D.B.; Guichard, F. Recovery processes and factors limiting cloud-top height following the arrival of a dry intrusion observed during TOGA-COARE. J. Atmos. Sci. 2002, 59, 2438–2457. [Google Scholar] [CrossRef]
- Derbyshire, S.H.; Beau, I.; Bechtold, P.; Grandpeix, J.Y.; Piriou, J.M.; Redelsperger, J.L.; Soares, P.M.M. Sensitivity of moist convection to environmental humidity. Q. J. R. Meteorol. Soc. 2004, 130, 3055–3079. [Google Scholar] [CrossRef]
- Sahany, S.; Neelin, J.D.; Hales, K.; Neale, R.B. Temperature-moisture dependence of the deep convective transition as a constraint on entrainment in climate models. J. Atmos. Sci. 2012, 69, 1340–1358. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Neelin, J.D.; Mechoso, C.R. Tropical Convective Transition Statistics and Causality in the Water Vapor-Precipitation Relation. J. Atmos. Sci. 2017, 74, 915–931. [Google Scholar] [CrossRef]
- Schiro, K.A.; Neelin, J.D. Deep Convective Organization, Moisture Vertical Structure, and Convective Transition Using Deep-Inflow Mixing. J. Atmos. Sci. 2019, 76, 965–987. [Google Scholar] [CrossRef]
- Haddad, Z.S.; Sawaya, R.C.; Kacimi, S.; Sy, O.O.; Turk, F.J.; Steward, J. Interpreting millimeter-wave radiances over tropical convective clouds. J. Geophys. Res. Atmos. 2017, 122, 1650–1664. [Google Scholar] [CrossRef]
- Wentz, F.J. A 17-Yr Climate Record of Environmental Parameters Derived from the Tropical Rainfall Measuring Mission (TRMM) Microwave Imager. J. Clim. 2015, 28, 6882–6902. [Google Scholar] [CrossRef]
- Adams, D.K.; Fernandes, R.M.; Holub, K.L.; Gutman, S.I.; Barbosa, H.M.; Machado, L.A.; Calheiros, A.J.; Bennett, R.A.; Kursinski, E.R.; Sapucci, L.F. The Amazon Dense GNSS Meteorological Network: A New Approach for Examining Water Vapor and Deep Convection Interactions in the Tropics. Bull. Am. Meteorol. Soc. 2015, 96, 2151–2165. [Google Scholar] [CrossRef]
- Ware, R.; Rocken, C.; Solheim, F.; Feng, D.; Herman, B.; Gorbunov, M.; Businger, S. GPS sounding of the atmosphere from low earth orbit: Preliminary results. Bull. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Sol.-Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Bauer, P.; Radnóti, G.; Healy, S.; Cardinali, C. GNSS Radio Occultation Constellation Observing System Experiments. Mon. Weather Rev. 2013, 142, 555–572. [Google Scholar] [CrossRef]
- Cucurull, L.; Atlas, R.; Li, R.; Mueller, M.J.; Hoffman, R.N. An Observing System Simulation Experiment with a Constellation of Radio Occultation Satellites. Mon. Weather Rev. 2018, 146, 4247–4259. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Schiro, K.A.; Neelin, J.D. Convective Transition Statistics over Tropical Oceans for Climate Model Diagnostics: Observational Baseline. J. Atmos. Sci. 2018, 75, 1553–1570. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; Wang, K.-N.; Ao, C.O.; Turk, F.J.; Torre-Juárez, M.D.L. Assessment of global navigation satellite system (GNSS) radio occultation refractivity under heavy precipitation. Atmos. Chem. Phys. 2018, 18, 11697–11708. [Google Scholar] [CrossRef] [Green Version]
- Biondi, R.; Randel, W.J.; Ho, S.-P.; Neubert, T.; Syndergaard, S. Thermal structure of intense convective clouds derived from GPS radio occultations. Atmos. Chem. Phys. Discuss. 2011, 11, 29093–29116. [Google Scholar] [CrossRef]
- Murphy, M.J.; Haase, J.S.; Padullés, R.; Chen, S.-H.; Morris, M.A. The Potential for Discriminating Microphysical Processes in Numerical Weather Forecasts Using Airborne Polarimetric Radio Occultations. Remote Sens. 2019, 11, 2268. [Google Scholar] [CrossRef]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio occultation and ground-based GNSS products for observing, understanding and predicting extreme events: A review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Cardellach, E.; Oliveras, S.; Rius, A.; Tomás, S.; Ao, C.O.; Franklin, G.W.; Iijima, B.A.; Kuang, D.; Meehan, T.K.; Padullés, R.; et al. Sensing Heavy Precipitation with GNSS Polarimetric Radio Occultations. Geophys. Res. Lett. 2019, 46, 1024–1031. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document, version 4.5; NASA Precipitation Measuring Missions, Goddard Space Flight Center: Greenbelt, MD, USA, 2015. Available online: http://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.5.pdf (accessed on 11 October 2019).
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and their application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Zeng, Z.; Sokolovskiy, S.; Schreiner, W.S.; Hunt, D. Representation of Vertical Atmospheric Structures by Radio Occultation Observations in the Upper Troposphere and Lower Stratosphere: Comparison to High-Resolution Radiosonde Profiles. J. Atmos. Ocean. Technol. 2019, 36, 655–670. [Google Scholar] [CrossRef]
- Healy, S.B.; Eyre, J.R. Retrieving temperature, water vapour and surface pressure information from refractive-index profiles derived by radio occultation: A simulation study. Q. J. R. Meteorol. Soc. 2000, 126, 1661–1683. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A. A comparison of water vapor derived from GPS occultations and global weather analyses. J. Geophys. Res. Atmos. 2001, 106, 1113–1138. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Gebhardt, T. A Method to Deconvolve Errors in GPS RO-Derived Water Vapor Histograms. J. Atmos. Ocean. Technol. 2014, 31, 2606–2628. [Google Scholar] [CrossRef]
- Vergados, P.; Mannucci, A.J.; Ao, C.O. Assessing the performance of GPS radio occultation measurements in retrieving tropospheric humidity in cloudiness: A comparison study with radiosondes, ERA-Interim, and AIRS data sets. J. Geophys. Res. Atmos. 2014, 119, 7718–7731. [Google Scholar] [CrossRef]
- Juárez, M.D.L.T.; Padullés, R.; Turk, F.J.; Cardellach, E. Signatures of Heavy Precipitation on the Thermodynamics of Clouds Seen from Satellite: Changes Observed in Temperature Lapse Rates and Missed by Weather Analyses. J. Geophys. Res. Atmos. 2018, 123, 13033–13045. [Google Scholar]
- Cardellach, E.; Tomás, S.; Oliveras, S.; Padullés, R.; Rius, A.; Juárez, M.; Turk, F.J.; Ao, C.O.; Kursinki, E.R.; Schreiner, R.; et al. Sensitivity of PAZ LEO Polarimetric GNSS Radio-Occultation Experiment to Precipitation Events. IEEE Trans. Geosci. Remote Sens. 2015, 53, 190–206. [Google Scholar] [CrossRef]
- Cardellach, E.; Padullés, R.; Tomás, S.; Turk, F.J.; Ao, C.O.; Torre-Juárez, M.D.L. Probability of intense precipitation from polarimetric GNSS radio occultation observations. Q. J. R. Meteorol. Soc. 2018, 144, 206–220. [Google Scholar] [CrossRef] [PubMed]
- Padullés, R.; Ao, C.O.; Turk, F.J.; de la Torre-Juárez, M.; Wang, K.-N.; Iijima, B.; Cardellach, E. Calibration and Validation of the Polarimetric Radio Occultation and Heavy Precipitation experiment Aboard the PAZ Satellite. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef]
- Andrić, J.; Kumjian, M.R.; Zrnić, D.S.; Straka, J.M.; Melnikov, V.M. Polarimetric Signatures above the Melting Layer in Winter Storms: An Observational and Modeling Study. J. Appl. Meteor. Climatol. 2013, 52, 682–700. [Google Scholar] [CrossRef]
- Anthes, R.; Schreiner, W. Six new satellites watch the atmosphere over Earth’s equator. Eos 2019, 100. [Google Scholar] [CrossRef]
- Esterhuizen, S.; Franklin, G.; Hurst, K.; Mannucci, A.; Meehan, T.; Webb, F.; Young, L. TriG—A GNSS Precise Orbit and Radio Occultation Space Receiver. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1442–1446. [Google Scholar]
- Franklin, G.; Esterhuizen, S.; Galley, C.; Iijima, B.; Larsen, K.; Lee, M.; Liu, J.; Meehan, T.; Young, L. A GNSS receiver for small satellites enabling precision POD, radio occultations, and reflections. In CubeSats and NanoSats for Remote Sensing II; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 1076905. [Google Scholar]
- Jasper, L.; Nuding, D.; Barlow, E.; Hogan, E.; O’Keefe, S.; Withnell, P.; Yunck, T. CICERO: A Distributed Small Satellite Radio Occultation Pathfinder Mission. In Proceedings of the 27th AIAA/USU Conference, Small Satellite Constellations, Logan, UT, USA, 10–15 August 2013; Paper SSC13-IV-5. Available online: http://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=2936&context=smallsat (accessed on 11 October 2019).
- Ao, C.O.; Hajj, G.A.; Meehan, T.K.; Dong, D.; Iijima, B.A.; Mannucci, A.J.; Kursinski, E.R. Rising and setting GPS occultations by use of open-loop tracking. J. Geophys. Res. Atmos. 2009, 114, D04101. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Weather Radar: Principles and Applications; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Foelsche, U.; Syndergaard, S.; Fritzer, J.; Kirchengast, G. Errors in GNSS radio occultation data: Relevance of the measurement geometry and obliquity of profiles. Atmos. Meas. Tech. 2011, 4, 189–199. [Google Scholar] [CrossRef]
- Peral, E.; Im, E.; Wye, L.; Lee, S.; Tanelli, S.; Rahmat-Samii, Y.; Horst, S.; Hoffman, J.; Yun, S.; Imken, T.; et al. Radar Technologies for Earth Remote Sensing from CubeSat Platforms. Proc. IEEE 2018, 106, 404–418. [Google Scholar] [CrossRef]
- Möller, G.; Landskron, D. Atmospheric bending effects in GNSS tomography. Atmos. Meas. Tech. 2019, 12, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Geer, A.J.; Baordo, F.; Bormann, N.; Chambon, P.; English, S.J.; Kazumori, M.; Lawrence, H.; Lean, P.; Lonitz, K.; Lupu, C. The growing impact of satellite observations sensitive to humidity, cloud and precipitation. Q. J. R. Meteorol. Soc. 2017, 143, 3189–3206. [Google Scholar] [CrossRef]
- Faber, A.; Llamedo, P.; Schmidt, T.; De La Torre, A.; Wickert, J. On the determination of gravity wave momentum flux from GPS radio occultation data. Atmos. Meas. Tech. 2013, 6, 3169–3180. [Google Scholar] [CrossRef] [Green Version]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turk, F.J.; Padullés, R.; Ao, C.O.; Juárez, M.d.l.T.; Wang, K.-N.; Franklin, G.W.; Lowe, S.T.; Hristova-Veleva, S.M.; Fetzer, E.J.; Cardellach, E.; et al. Benefits of a Closely-Spaced Satellite Constellation of Atmospheric Polarimetric Radio Occultation Measurements. Remote Sens. 2019, 11, 2399. https://doi.org/10.3390/rs11202399
Turk FJ, Padullés R, Ao CO, Juárez MdlT, Wang K-N, Franklin GW, Lowe ST, Hristova-Veleva SM, Fetzer EJ, Cardellach E, et al. Benefits of a Closely-Spaced Satellite Constellation of Atmospheric Polarimetric Radio Occultation Measurements. Remote Sensing. 2019; 11(20):2399. https://doi.org/10.3390/rs11202399
Chicago/Turabian StyleTurk, F. Joseph, Ramon Padullés, Chi O. Ao, Manuel de la Torre Juárez, Kuo-Nung Wang, Garth W. Franklin, Stephen T. Lowe, Svetla M. Hristova-Veleva, Eric J. Fetzer, Estel Cardellach, and et al. 2019. "Benefits of a Closely-Spaced Satellite Constellation of Atmospheric Polarimetric Radio Occultation Measurements" Remote Sensing 11, no. 20: 2399. https://doi.org/10.3390/rs11202399
APA StyleTurk, F. J., Padullés, R., Ao, C. O., Juárez, M. d. l. T., Wang, K. -N., Franklin, G. W., Lowe, S. T., Hristova-Veleva, S. M., Fetzer, E. J., Cardellach, E., Kuo, Y. -H., & Neelin, J. D. (2019). Benefits of a Closely-Spaced Satellite Constellation of Atmospheric Polarimetric Radio Occultation Measurements. Remote Sensing, 11(20), 2399. https://doi.org/10.3390/rs11202399