Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. The NT Algorithm
2.2. The ASI Algorithm
2.3. The VASIA2 Algorithm
- Three tangents tg(85–19 V), tg(85–37 H), tg(37–19 V) are calculated from microwave satellite data.
- Criterion function F1 is constructed. It is the sum of squared coefficients of variation between the theoretical dependencies of tangents (14) and (15) and the satellite data tangents tg(85–19 V) and tg(85–37 H):
- Criterion function F1 is calculated for SIC from 0 to 10 tenths with a step equal to 0.1.
- The minimum value of the criterion function F1 determines I1—the SIC with no error correction related to SWM on ice.
- At the given I1, for each pixel the value obtained by (18) is compared to satellite data tangent tg(37–19 V):
- Ifthen the SIC is taken equal to the one determined at Step 4: I2 = I1.
- Ifthen the criterion function F2 is constructed as the sum of squared coefficients of variation between the theoretical tangent values (16) and (17) and the satellite data tangents tg(85–19 V) and tg(85–37 H):
- For the interval of SIC from 0 to 10, the minimum value of criterion function F2 is found.
- The minimum value of criterion function F2 determines the resulting SIC value I2.
2.4. Microwave Satellite Data
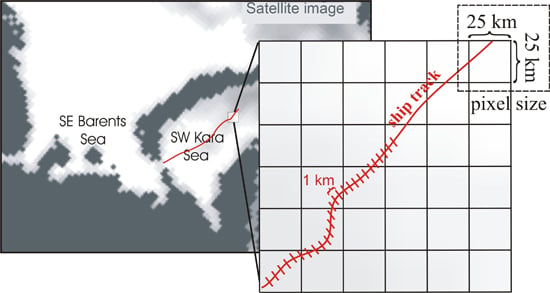
2.5. Dedicated Ship Observations
3. Results
3.1. Difference between Csmr and Cso
3.2. Difference between Csmr and Cso-ni
3.3. Stages of Ice Melt
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Basics of Ship Ice Observations

Collecting Information on Sea Ice Parameters
- -
- total SIC;
- -
- partial SIC of each ice type presented in the area;
- -
- size of ice formations of each ice type;
- -
- ice ridging over the whole area;
- -
- melt stage;
- -
- leads and cracks and their orientation relative to the ship course.
- -
- total SIC;
- -
- partial SIC of each ice type presented in the area;
- -
- size of ice formations of each ice type;
- -
- thickness of each ice type;
- -
- snow depth on surface of each ice type;
- -
- ice ridging;
- -
- young ice rafting;
- -
- melt stage;
- -
- occurrence and intensity of ice compression;
- -
- icebergs concentration, their shape and size.
Estimating Total SIC
Estimating Partial SICs
- -
- new ice (frazil ice, ice grease, slush, shuga);
- -
- nilas: pancake ice, dark nilas (3–5 cm) and light nilas (5–10 cm);
- -
- young ice: grey ice (10–15 cm) and grey-white ice (15–30 cm);
- -
- thin first-year ice: first stage (30–50 cm) and second stage (50–70 cm);
- -
- medium first-year ice (70–120 cm);
- -
- thick first-year ice (120 ~ 200 cm);
- -
- old ice: second-year and multi-year ice, old ice thickness varies depending on the region and season and may reach over 200 cm.
Definition of Melt Stage
| Stage | Visible Sea Ice Melt Characteristics | Examples (Photos by T.A. Alekseeva Taken during the Arctic Expeditions) |
|---|---|---|
| 0 | No melt |  |
| 1 | Few melt ponds and dark patches are detected on the sea surface. Ice breccias begin to disintegrate. |  |
| 2 | Ice surface is darkened, snow is partly melted, many large melt ponds are visible. |  |
| 3 | Ponds are everywhere. Snow is melted completely. Thaw holes appear. Ice gets dried and whitens (photo shows melt stage 3, but ice is covered by fresh recent snow). |  |
| 4 | Heavily decayed ice. Thaw holes and water separations are everywhere, ice breccias have completely disintegrated. Mushroom ice with underwater rams appears among ice floes. |  |
| 5 | Strongly ablated deformed ice pieces sitting deep in water predominate. Ice is heavily flooded and has grayish color. |  |
Appendix B
- -
- data source (one of the DMSP instruments: F8, F10, F11, Fl2, F13, F14, F15, …);
- -
- data channel (from one to seven SSM/I or SSMIS channels);
- -
- interval of observation (year, month and date of start and end of the measurement);
- -
- zone of observations (global coverage or a rectangle with specified boundary latitudes and longitudes);
- -
- scale of spatial averaging (a regular grid step in degrees and fractions of degree with independently set latitude and longitude);
- -
- scale of time averaging in days (used for accumulating and averaging the data of successive satellite surveys of the selected area of the Earth).
References
- Przybylak, R. The Climate of the Arctic; Springer: Dordrecht, The Netherlands, 2003; p. 271. [Google Scholar]
- Vavrus, S.; Harrison, S.P. The impact of sea-ice dynamics on the Arctic climate system. Clim. Dyn. 2003, 20, 741–757. [Google Scholar] [CrossRef]
- Frolov, I.E.; Gudkovich, Z.M.; Karklin, V.P.; Kovalev, E.G.; Smolyanitsky, M.V. Climate Change in Eurasian Arctic Shelf Seas—Centennial Ice Cover Observations; Springer: Berlin, Germany, 2009; p. 166. [Google Scholar]
- Smith, L.C.; Stephenson, S.R. New Trans-Arctic shipping routes navigable by midcentury. Proc. Natl. Acad. Sci. USA 2013, 110, 4871. [Google Scholar] [CrossRef] [PubMed]
- Laliberté, F.; Howell, S.E.L.; Kushner, P.J. Regional variability of a projected sea ice-free Arctic during the summer months. Geophys. Res. Lett. 2016, 43, 256–263. [Google Scholar] [CrossRef]
- Tedesco, M. Remote Sensing of the Cryosphere, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tikhonov, V.V.; Raev, M.D.; Sharkov, E.A.; Boyarskii, D.A.; Repina, I.A.; Komarova, N.Y. Satellite microwave radiometry of sea ice of polar regions: A review. Izv. Atmos. Ocean. Phys. 2016, 52, 1012–1030. [Google Scholar] [CrossRef]
- Alekseeva, T.A.; Frolov, S.V. Comparative analysis of satellite and shipborne data on ice cover in the Russian Arctic seas. Izv. Atmos. Ocean. Phys. 2013, 49, 879–885. [Google Scholar] [CrossRef]
- Meier, W. Comparison of passive microwave ice concentration algorithm retrievals with AVHRR imagery, in Arctic peripheral seas. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1324–1337. [Google Scholar] [CrossRef]
- Wiebe, H.; Heygster, G.; Markus, T. Comparison of the ASI Ice Concentration Algorithm with Landsat-7 ETM+ and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3008–3015. [Google Scholar] [CrossRef]
- Pang, X.; Pu, J.; Zhao, X.; Ji, Q.; Qu, M.; Cheng, Z. Comparison between AMSR2 Sea Ice Concentration Products and Pseudo-Ship Observations of the Arctic and Antarctic Sea Ice Edge on Cloud-Free Days. Remote Sens. 2018, 10, 317. [Google Scholar] [CrossRef]
- Agnew, T.A.; Howell, S. Comparison of digitized Canadian ice charts and passive microwave sea-ice concentrations. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 231, pp. 231–233. [Google Scholar]
- Agnew, T.; Howell, S. The use of operational ice charts for evaluating passive microwave ice concentration data. Atmos. Ocean 2003, 41, 317–331. [Google Scholar] [CrossRef]
- Tonboe, R.T.; Eastwood, S.; Lavergne, T.; Sørensen, A.M.; Rathmann, N.; Dybkjær, G.; Pedersen, L.T.; Høyer, J.L.; Kern, S. The EUMETSAT sea ice concentration climate data record. Cryosphere 2016, 10, 2275–2290. [Google Scholar] [CrossRef] [Green Version]
- Andersen, S.; Tonboe, R.; Kern, S.; Schyberg, H. Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: An intercomparison of nine algorithms. Remote Sens. Environ. 2006, 104, 374–392. [Google Scholar] [CrossRef]
- Ivanova, N.; Johannessen, O.; Pedersen, L.; Tonboe, R. Retrieval of Arctic Sea Ice Parameters by Satellite Passive Microwave Sensors: A Comparison of Eleven Sea Ice Concentration Algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7233–7246. [Google Scholar] [CrossRef]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef]
- Zabolotskikh, E.V. Review of Methods to Retrieve Sea-Ice Parameters from Satellite Microwave Radiometer Data. Izv. Atmos. Ocean Phys. 2019, 55, 110–128. [Google Scholar] [CrossRef]
- Comiso, J.C.; Ackley, S.F.; Gordon, A.L. Antarctic sea ice microwave signatures and their correlation with in situ ice observations. J. Geophys. Res. Oceans 1984, 89, 662–672. [Google Scholar] [CrossRef]
- Knuth, M.A.; Ackley, S.F. Summer and early-fall Sea-ice concentration in the Ross Sea: Comparison of in Situ ASPeCt observations and satellite passive microwave estimates. Ann. Glaciol. 2006, 44, 303–309. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89-GHz channels. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Beitsch, A.; Kern, S.; Kaleschke, L. Comparison of SSM/I and AMSR-E Sea Ice Concentrations with ASPeCt Ship Observations Around Antarctica. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1985–1996. [Google Scholar] [CrossRef]
- Ozsoy-Cicek, B.; Ackley, S.F.; Worby, A.; Xie, H.; Lieser, J. Antarctic sea-ice extents and concentrations: Comparison of satellite and ship measurements from International Polar Year cruises. Ann. Glaciol. 2011, 52, 318–326. [Google Scholar] [CrossRef]
- Worby, A.P.; Allison, I. A Technique for Making Ship-Based Observations of Antarctic Sea-Ice Thicknes and Characteristics—Part I: Observational Techniques and Results; Antarctic Cooperative Research Center, University of Tasmania: Hobart, Australia, 1999; p. 63. [Google Scholar]
- Tikhonov, V.V.; Boyarskii, D.A.; Repina, I.A.; Raev, M.D.; Sharkov, E.A.; Alexeeva, T.A. Snow Cover Effect on Brightness Temperature of Arctic Ice Fields Based on SSM/I Data. In Proceedings of the Progress in Electromagnetics Research Symposium, PIERS Proceedings, Stockholm, Sweden, 12–15 August 2013; pp. 514–518. [Google Scholar]
- Tikhonov, V.V.; Boyarskii, D.A.; Sharkov, E.A.; Raev, M.D.; Repina, I.A.; Ivanov, V.V.; Alexeeva, T.A.; Komarova, N.Y. Microwave Model of Radiation from the Multilayer “Ocean-Atmosphere” System for Remote Sensing Studies of the Polar Regions. Prog. Electromagn. Res. B 2014, 59, 123–133. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Gloersen, P.; Wilheit, T.T. Aircraft and Satellite Passive Microwave Observations of the Bering Sea Ice Cover During MIZEX West. IEEE Trans. Geosci. Remote Sens. 1986, 3, 368–377. [Google Scholar] [CrossRef]
- Windnagel, A. Climate Algorithm Theoretical Basis Document (C-ATBD). Sea Ice Concentration. Climate Data Record (CDR) Program; CDR Program Document Number CDRP-ATBD-0107; National Oceanic and Atmospheric Administration (NOAA): Silver Spring, MD, USA, 2018. [Google Scholar]
- Cavalieri, D.J.; Germain, K.M.; Swift, C.T. Reduction of weather effects in the calculation of sea-ice concentration with the DMSP SSM/I. J. Glaciol. 1995, 41, 455–464. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C. Sea ice effective microwave emissivities from satellite passive microwave and infrared observations. J. Geophys. Res. Oceans 1983, 88, 7686–7704. [Google Scholar] [CrossRef]
- Kaleschke, L.; Lupkes, C.; Vihma, T.; Haarpaintner, J.; Bochert, A.; Hartmann, J.; Heygster, G. SSM/I Sea Ice Remote Sensing for Mesoscale Ocean-Atmosphere Interaction Analysis. Can. J. Remote Sens. 2001, 27, 526–537. [Google Scholar] [CrossRef]
- Svendsen, E.; Matzler, C.; Grenfell, T.C. A model for retrieving total sea ice concentration from a spaceborne dual-polarized passive microwave instrument operating near 90 GHz. Int. J. Remote Sens. 1987, 8, 1479–1487. [Google Scholar] [CrossRef]
- Kaleschke, L. Fernerkundung des Meereises mit Passiven und Aktiven Mikrowellensensoren. Ph.D. Thesis, Universität Bremen, Bremen, Germany, 2003. [Google Scholar]
- Pease, C.H. The size of wind-driven coastal polynyas. J. Geophys. Res. Oceans 1987, 92, 7049–7059. [Google Scholar] [CrossRef]
- Comiso, J.C. SSM/I ice concentrations using the Bootstrap algorithm; NASA Reference Publication 1380; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1995. [Google Scholar]
- Tikhonov, V.V.; Repina, I.A.; Raev, M.D.; Sharkov, E.A.; Boyarskii, D.A.; Komarova, N.Y. Integrative algorithm of determining ice conditions in Polar Regions by data of satellite microwave radiometry (VASIA2). Izv. Atmos. Ocean Phys. 2015, 51, 914–928. [Google Scholar] [CrossRef]
- Tikhonov, V.V.; Repina, I.A.; Raev, M.D.; Sharkov, E.A.; Ivanov, V.V.; Boyarskii, D.A.; Alexeeva, T.A.; Komarova, N.Y. A physical algorithm to measure sea ice concentration from passive microwave remote sensing data. Adv. Space Res. 2015, 56, 1578–1589. [Google Scholar] [CrossRef]
- Gray, D.M.; Male, D.H. Handbook of Snow: Principles, Processes, Management & Use; Pergamon Press: Oxford, UK, 1981; p. 776. [Google Scholar]
- Serreze, M.C.; Barry, R.G. The Arctic Climate System; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Turner, J.; Bindschadler, R.A.; Convey, P.; Di Prisco, G.; Fahrbach, E.; Gutt, J.; Hodgson, D.A.; Mayewski, P.A.; Summerhayes, C.P. Antarctic Climate Change and the Environment; The International Council for Science: Paris, France, 2009; p. 526. [Google Scholar]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2010; p. 704. [Google Scholar]
- Barry, R.; Gan, T.Y. The Global Cryosphere: Past, Present and Future; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Singh, V.P.; Singh, P.; Haritashya, U.K. The Encyclopedia of Snow, Ice and Glaciers; Springer: Berlin, Germany, 2011; p. 1254. [Google Scholar]
- Kuz’min, P.P. The Physical Properties of Snow Cover; Nauka: Moscow, Russia, 1957; p. 180. (In Russian) [Google Scholar]
- Kotlyakov, V.M. Izbrannye Sochineniya. Kniga 1. Glyatsiologiya Antarktidy; Nauka: Moscow, Russia, 2000; p. 432. [Google Scholar]
- Tschudi, M.A.; Maslanik, J.A.; Perovich, D.K. Derivation of melt pond coverage on Arctic sea ice using MODIS observations. Remote Sens. Environ. 2008, 112, 2605–2614. [Google Scholar] [CrossRef]
- Polashenski, C.; Perovich, D.; Courville, Z. The mechanisms of sea ice melt pond formation and evolution. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L. Exceptional melt pond occurrence in the years 2007 and 2011 on the Arctic sea ice revealed from MODIS satellite data. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L.; Birnbaum, G. Melt ponds on Arctic sea ice determined from MODIS satellite data using an artificial neural network. Cryosphere 2012, 6, 431–446. [Google Scholar] [CrossRef] [Green Version]
- Istomina, L.; Heygster, G.; Huntemann, M.; Schwarz, P.; Birnbaum, G.; Scharien, R.; Polashenski, C.; Perovich, D.; Zege, E.; Malinka, A.; et al. Melt pond fraction and spectral sea ice albedo retrieval from MERIS data—Part 1: Validation against in situ, aerial, and ship cruise data. Cryosphere 2015, 9, 1551–1566. [Google Scholar] [CrossRef]
- Istomina, L.; Heygster, G.; Huntemann, M.; Marks, H.; Melsheimer, C.; Zege, E.; Malinka, A.; Prikhach, A.; Katsev, I. Melt pond fraction and spectral sea ice albedo retrieval from MERIS data—Part 2: Case studies and trends of sea ice albedo and melt ponds in the Arctic for years 2002–2011. Cryosphere 2015, 9, 1567–1578. [Google Scholar] [CrossRef]
- Morassutti, M.P.; Ledrew, E.F. Albedo and depth of melt ponds on sea-ice. Int. J. Climatol. 1996, 16, 817–838. [Google Scholar] [CrossRef]
- Perovich, D.K.; Grenfell, T.C.; Richter-Menge, J.A.; Light, B.; Tucker, W.B., III; Eicken, H. Thin and thinner: Sea ice mass balance measurements during SHEBA. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Tucker, W.B., III; Gow, A.J.; Meese, D.A.; Bosworth, H.W.; Reimnitz, E. Physical characteristics of summer sea ice across the Arctic Ocean. J. Geophys. Res. Oceans 1999, 104, 1489–1504. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Zwally, H.; Meier, W.; Fetterer, F.; Knowles, K.; Savoie, M.; Brodzik, M. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1. Available online: https://nsidc.org/data/nsidc-0051 (accessed on 15 February 2007).
- Ezraty, R.; Girard-Ardhuin, F.; Piolle, J.-F.; Kaleschke, L.; Heygster, G. Arctic and Antarctic Sea Ice Concentration and Arctic Drift Estimates from Special Sensor Microwave Data—User’s Manual; Version 2.1; IFREMER: Brest, France, 2007. [Google Scholar]
- Ermakov, D.M.; Raev, M.D.; Suslov, A.I.; Sharkov, E.A. Electronic long-standing database for the global radiothermal field of the Earth in context of multi-scale investigation of the atmosphere-ocean system. Issled. Zemli Kosm. 2007, 1, 7–13. (In Russian) [Google Scholar]
- AARI. Guidance to Special Shipborne Ice Observations; AARI: Saint-Petersburg, Russia, 2011; 42p. [Google Scholar]
- Shokr, M.; Sinha, N. Sea Ice: Physics and Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA; American Geophysical Union: Washington, DC, USA, 2015. [Google Scholar]
- Heygster, G.; Huntemann, M.; Ivanova, N.; Saldo, R.; Pedersen, L.T. Response of passive microwave sea ice concentration algorithms to thin ice. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3618–3621. [Google Scholar]
- Kern, S.; Rösel, A.; Pedersen, L.T.; Ivanova, N.; Saldo, R.; Tonboe, R.T. The impact of melt ponds on summertime microwave brightness temperatures and sea-ice concentrations. Cryosphere 2016, 10, 2217–2239. [Google Scholar] [CrossRef] [Green Version]
- Comiso, J.C.; Kwok, R. Surface and radiative characteristics of the summer Arctic sea ice cover from multisensor satellite observations. J. Geophys. Res. Oceans 1996, 101, 28397–28416. [Google Scholar] [CrossRef]
- Steffen, K.; Maslanik, J.A. Comparison of Nimbus 7 scanning multichannel microwave radiometer radiance and derived sea ice concentrations with Landsat imagery for the north water area of Baffin Bay. J. Geophys. Res. Oceans 1988, 93, 10769–10781. [Google Scholar] [CrossRef]
- Steffen, K.; Schweiger, A. NASA team algorithm for sea ice concentration retrieval from Defense Meteorological Satellite Program special sensor microwave imager: Comparison with Landsat satellite imagery. J. Geophys. Res. Oceans 1991, 96, 21971–21987. [Google Scholar] [CrossRef]

















| Summer (expeditions during the ice melt period in July–mid-September) | ||
| Vessel, Year | Period of observation | Area of observation |
| Mikhail Somov, 1996 | 24–27 September | Laptev Sea |
| Akademik Fedorov, 2000 | 14 August–13 September | East Siberian, Laptev, Kara Seas |
| Sovetskiy Soyuz, 2003 | 25 July–15 September | East Siberian, Laptev, Kara Seas |
| Kapitan Dranitsyn, 2003 | 30 August–13 September | East Siberian, Laptev, Kara Seas |
| Akademik Fedorov, 2004 | 25 August–10 September | East Siberian, Laptev, Kara Seas |
| Akademik Fedorov, 2005 | 19 July–10 September | East Siberian, Laptev, Kara Seas |
| Winter (expeditions during freeze up and maximal development of the ice cover) | ||
| Vessel, Year | Period of observation | Area of observation |
| Mikhail Somov, 1996–1997 | 17 October–23 January | Barents, Kara, Laptev Seas |
| Mikhail Somov, 1997–1998 | 23 October–18 April | Barents, Kara, Laptev Seas |
| Mikhail Somov, 1998 | 9 October–25 December | Barents, Kara Seas |
| Kapitan Dranitsyn, 1998 | 27 April–13 May | Barents, Kara Seas |
| Kapitan Dranitsyn, 2000 | 13–24 February | Barents, Kara Seas |
| Mikhail Somov, 2001 | 7–27 April | Barents Sea |
| Mikhail Somov, 2003 | 5 April–20 May | Barents Sea |
| Mikhail Somov, 2004 | 10 April–10 May | Barents Sea |
| Summer | |||
| NT (25 km) Cso/Cso-ni (8% of new ice and nilas in total Cso) | ASI (12.5 km) Cso/Cso-ni (9% of new ice and nilas in total Cso) | VASIA2 (12.5 km) Cso/Cso-ni (9% of new ice and nilas in total Cso) | |
| Coefficient of determination (R2) | 0.74/0.71 | 0.81/0.79 | 0.65/0.62 |
| Average error, tenths | −0.4/0.0 | −0.3/+0.1 | −0.3/+0.1 |
| Standard deviation, tenths | 2.1/2.1 | 1.8/1.9 | 2.6/2.8 |
| Winter | |||
| NT (25 km) Cso/Cso-ni(24% of new ice and nilas in total Cso) | ASI (12.5 km) Cso/Cso-ni(28% of new ice and nilas in total Cso) | VASIA2 (12.5 km) Cso/Cso-ni(28% of new ice and nilas in total Cso) | |
| Coefficient of determination (R2) | 0.73/0.59 | 0.62/0.62 | 0.46/0.37 |
| Average error, tenths | −0.4/+1.1 | −0.8/+1.0 | +0.2/+1.4 |
| Standard deviation, tenths | 2.2/2.6 | 2.7/2.6 | 2.6/3.0 |
| Melt | NT | ASI | VASIA2 |
|---|---|---|---|
| 5 Strongly ablated deformed ice pieces sitting deep in water predominate. Ice is heavily flooded and has grayish color. | −1.3/−1.7 | −1.1/−0.1 | −0.6/0.1 |
| 4 Heavily decayed ice. Thaw holes and water separations are everywhere, ice breccias have completely disintegrated. Mushroom ice with underwater rams appears among ice floes. | −1.2/−2.7 | −2.1/−1.7 | −1.4/−0.4 |
| 3 Ponds are everywhere. Snow is melted completely. Thaw holes appear. Ice gets dried and whitens. | −1.0/−1.7 | −0.5/−1.2 | −0.5/−0.7 |
| 2 Ice surface is darkened, snow is partly melted, many large melt ponds are visible. | −1.1/−1.8 | −0.3/−1.0 | −0.2/−1.1 |
| 1 Few melt ponds and dark patches are detected on the sea surface. Ice breccias begin to disintegrate. | −1.8/−1.8 | −0.1/−0.4 | 0.4/0.1 |
| 0 No visible evidence of melt, however the most probably that snow cover is moist. | −1.5/−1.5 | −0.5/−0.8 | 0.1/−2.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alekseeva, T.; Tikhonov, V.; Frolov, S.; Repina, I.; Raev, M.; Sokolova, J.; Sharkov, E.; Afanasieva, E.; Serovetnikov, S. Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data. Remote Sens. 2019, 11, 2481. https://doi.org/10.3390/rs11212481
Alekseeva T, Tikhonov V, Frolov S, Repina I, Raev M, Sokolova J, Sharkov E, Afanasieva E, Serovetnikov S. Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data. Remote Sensing. 2019; 11(21):2481. https://doi.org/10.3390/rs11212481
Chicago/Turabian StyleAlekseeva, Tatiana, Vasiliy Tikhonov, Sergei Frolov, Irina Repina, Mikhael Raev, Julia Sokolova, Evgeniy Sharkov, Ekaterina Afanasieva, and Sergei Serovetnikov. 2019. "Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data" Remote Sensing 11, no. 21: 2481. https://doi.org/10.3390/rs11212481
APA StyleAlekseeva, T., Tikhonov, V., Frolov, S., Repina, I., Raev, M., Sokolova, J., Sharkov, E., Afanasieva, E., & Serovetnikov, S. (2019). Comparison of Arctic Sea Ice Concentrations from the NASA Team, ASI, and VASIA2 Algorithms with Summer and Winter Ship Data. Remote Sensing, 11(21), 2481. https://doi.org/10.3390/rs11212481