Statistical Stability and Spatial Instability in Mapping Forest Tree Species by Comparing 9 Years of Satellite Image Time Series

Abstract

Mapping forest composition using multiseasonal optical time series remains a challenge. Highly contrasted results are reported from one study to another suggesting that drivers of classification errors are still under-explored. We evaluated the performances of single-year Formosat-2 time series to discriminate tree species in temperate forests in France and investigated how predictions vary statistically and spatially across multiple years. Our objective was to better estimate the impact of spatial autocorrelation in the validation data on measurement accuracy and to understand which drivers in the time series are responsible for classification errors. The experiments were based on 10 Formosat-2 image time series irregularly acquired during the seasonal vegetation cycle from 2006 to 2014. Due to lot of clouds in the year 2006, an alternative 2006 time series using only cloud-free images has been added. Thirteen tree species were classified in each single-year dataset based on the Support Vector Machine (SVM) algorithm. The performances were assessed using a spatial leave-one-out cross validation (SLOO-CV) strategy, thereby guaranteeing full independence of the validation samples, and compared with standard non-spatial leave-one-out cross-validation (LOO-CV). The results show relatively close statistical performances from one year to the next despite the differences between the annual time series. Good agreements between years were observed in monospecific tree plantations of broadleaf species versus high disparity in other forests composed of different species. A strong positive bias in the accuracy assessment (up to 0.4 of Overall Accuracy (OA)) was also found when spatial dependence in the validation data was not removed. Using the SLOO-CV approach, the average OA values per year ranged from 0.48 for 2006 to 0.60 for 2013, which satisfactorily represents the spatial instability of species prediction between years.

1. Introduction

Forest ecosystems play a major role in global biodiversity [1]. They provide several services to humanity including carbon sequestration (which regulates climate [2]), timber production [3], soil protection [4], and recreation. They also have an impact on human health and well-being. However, the provision of such ecosystem services depends on several factors including the diversity of tree species [5]. Therefore, knowing the distribution of tree species in forests is crucial to assess ecosystem functions and services. More broadly, information on tree species is required for forest management and also for long-term forest monitoring, especially in the current context of climate change and related disturbances (forest fires, windstorms, drought, pests and diseases) [6].

Remote sensing has long been used to collect information on forest resources including stand composition [7,8]. Nevertheless, accurately distinguishing tree species is still challenging [9]. In the past, maps of tree species were based on field surveys completed by computer-aided analysis of aerial photographs [10,11]. While this approach provides accurate operational results for forest managers, it is limited to small spatial extent because it is costly and time consuming, which also affects its updating. In the last few decades, various types of remotely sensed images have been used to automate the identification of forest tree species. Some authors focused on the spatial resolution using very high-resolution satellite or airborne imagery [12,13,14,15]. They assumed the classification would benefit from the spatially detailed information and would therefore be accurate. Despite some successful results, this approach revealed itself to be of limited interest when only a single date was used due to the low spectral resolution of the data because of the reduced spectral and temporal information. Alternatively, as tree morphology and biochemical traits have a subtle influence on spectral reflectance [16], several authors explored airborne hyperspectral imagery [17,18,19]. Depending on the number of classes of species, on the methodology used for classification, and on the characteristics of the images (pixel size, number of spectral bands), the accuracy of the classification varied. Nevertheless, studies based on hyperspectral imagery were typically more accurate than those based on single-date multispectral data [9].

Taking advantage of the temporal dimension of the satellite data was another way to separate tree species [9]. Time series can capture the phenological behavior of the vegetation and this functional trait can be useful to discriminate the forest types. Changes in pigment contents, water and leaf morphology across seasons can vary from one species to another. Time series with images covering all phenological events from green-up to senescence (leaf-on, spring flush, autumn senescence, leaf-off) can produce detailed classification results. The use of multitemporal data for this purpose is not new. This approach has been explored from various image datasets of different spatial and temporal resolutions based on spaceborne sensors such as MODIS [20,21], Landsat [22,23,24,25,26], RapidEye [27], WorldView [28], as airborne sensor [29,30] or unmanned aerial systems [31]. More recently, the potential of the new freely available high spatial resolution Sentinel-2 (S2) data has been investigated [32,33,34,35,36]. In general, the authors found it advantageous to combine images acquired in spring and autumn, at the key phenological stages of temperate forests, since it had a positive influence on the accuracy of the classification. Images acquired in summer are also frequently selected in features ranking procedures, particularly for conifer species [36], but also for deciduous species [30]. From a spectral point of view, red-edge bands and SWIR bands are reported to be important variables when S2 time series are used [32,33,34].

Despite the increasing number of studies that use time series to identify forest types, the true predictive power of these kinds of data remain to be demonstrated. Even though it is difficult to compare studies because of the use of different methods, sensors, and classes of tree species, we observed very contrasted results from one study to another. For instance, using four dates for S2 data in 2017, Persson et al. [34] obtained a kappa value of 0.83 to classify five species (Norway spruce—Picea abies; Scots pine—Pinus sylvestris; Hybrid larch—Larix x marschlinsii; Birch—Betula sp. and Pedunculate Oak—Quercus robur). This differs substantially from the Immitzer’s results [32] (kappa = 0.59) as they used only two S2 images to map seven species including Norway spruce, Scots pine, European larch (Larix decidua) and Oak (Oak sp). There was also a difference of almost 0.2 points of overall accuracy (OA) between a study by Persson et al. [34] and one by Liu et al. [35] who classified eight types of forest in China with the same number of S2 images. In another study, using only two S2 images to separate 11 forest classes of broadleaves and conifers, Bolyn et al. [33] obtained very accurate results (OA of 0.93) in contrast with previous works but in line with others based on dense time series acquired using different sensors [27,37,38].

The notable difference in accuracy among past studies suggests a better understanding is required of the factors that affect the classification of species, as recommended by [9]. Several drivers of classification errors remain insufficiently explored, among which, spatial autocorrelation of reference data has long been identified but rarely quantified [39,40]. Spatial dependence in the reference data due to an inadequate sampling strategy to split training and validation sets can wrongly increase classification accuracy [39,41,42]. Despite different approaches addressing this issue by imposing a spatial stratification to select samples for training and testing [41,42], the spatial autocorrelation is not always estimated explicitely. This can lead to keep a residual spatial dependence between training and testing samples and not to fully eliminate the spatial overfitting. Contamination by clouds and cloud shadows in dense image high resolution time series may also have a major impact on classification performances. Because the distribution of such contamination may vary over time and in space across years, a multiyear analysis is required to reliably evaluate their effect.

The first objective of this study is to explore the stability of classification results in tree species discrimination from optical remotely sensed time series data of multiple years. The second objective is to understand the main drivers that affect the classification accuracy in this context. To our knowledge, this is the first study of variability between one-year classifications of tree species based on multiple years using dense image high spatial resolution time series. We evaluated the classification performance of single-year Formosat-2 time series in distinguishing forest types with spatially independent validation data. We also investigated how the predictions vary statistically and spatially across multiple years (from 2006 to 2014). The main contribution of this work is a better estimation of the classification accuracy of the forest maps by reducing optimistic bias due to spatial autocorrelation. The second contribution, resulting from the first, is a finer understanding of the drivers responsible for classification errors. We hypothesize that time series data improve species discrimination compared to single-date image due to seasonal variability in spectral reflectance between species.

2. Material

2.1. Study Area

The study site is located in south-western France, next to Toulouse, and covers an area of 24 km × 24 km (Figure 1). This delimited area was determined by a satellite acquisitions scheme by the Centre National d’Etudes Spatiales (CNES) who acquired a Formosat-2 Satellite Image Time Series (SITS) of the site. The Garonne river crosses the eastern part of the study area, influencing soil composition and the nearly flat topography of the area. The climate is sub-Atlantic characterized by sunny autumns, hot dry summers, and mild rainy winters (the average annual temperature is >13 °C; annual precipitation = 656 mm). The landscape is dominated by arable lands (including wheat, sunflower, maize) and grasslands. Forests cover up to 10% of the landscape (53 km${}^2$).

2.2. Satellite Image Time Series

We used a dense optical image dataset composed of Formosat-2 time series acquired in nine consecutive years from 2006 to 2014. This dataset was obtained during preparation for the Sentinel-2 and VEN$\mathsf{\mu }$S mission with cooperation between the Israeli Space Agency (ISA) and the French CNES [43]. A total of 156 dates was acquired with an average of 14 images per year and a maximum of 43 images in 2006. The distribution of the dates over time varied from one year to another and the number of images available during the growth season differed from the number available at the end of vegetation season (Figure 2).

Cloud coverage also varied considerably from one date to another, ranging from a minimum of 8 cloud-free images in 2011 to a maximum of 20 in 2006. For 2006, by visual inspection, we created an additional dataset (named 2006 bis) by selecting only the cloud-free images, resulting in a time series of 20 dates (compared to the original 46).

The Formosat-2 multispectral images are delivered in an 8-bit radiometric resolution. Each image provides 4 spectral bands ranging from the visible (Blue: 0.45–0.52 $\mathsf{\mu }$m, Green: 0.53–0.60 $\mathsf{\mu }$m, Red: 0.63–0.69 $\mathsf{\mu }$m) to the near-infrared (NIR: 0.76–0.90 $\mathsf{\mu }$m) with a nominal pixel size of 8 m. All the images were acquired under a constant viewing angle and a field of view of 24 km like Landsat, VEN$\mathsf{\mu }$S and Sentinel-2.

2.3. Ancillary Data

A forest mask produced in 1996 by the French National Forest Inventory database (IGN BDForêt^®, v.1) was used to select forest pixels in the SITS (i.e., forest stands with a minimum area of 2.25 hectares) and to exclude non-forested areas. Based on aerial photographs taken in 2006, 2010 and 2013 (IGN BDOrtho^®), the mask was manually updated to retain only SITS forest stands that remained stable over the nine year period

2.4. Field Data

Four field campaigns were conducted between November 2013 and January 2017 to identify and locate reference samples of tree species in the study site. All the main forests were visited. Only the dominant broadleaf and conifer tree species were recorded. To insure tree species purity in the training samples, plots were delimited at the center of homogeneous areas covering an area of approximatly 576 m${}^2$ (i.e., nine contiguous 8 m × 8 m Formosat-2 pixels). Only the pixel at the center of each area was used for the classification protocol. Plots were located using a Garmin GPSMap 62st receiver (3–5 m accuracy) and distributed over 72 distinct forest stands.

Thirteen tree species of which eight were broadleaf species and five conifer species were studied (

Table 1. List of tree species with their sample size, in pixels, collected during field surveys ($n=1262$). The number of forest stands in which the samples were collected is also provided. Stand delimitation is based on the French National Forest Inventory database (IGN BDForêt^® v.1).

Species	Sample Size	Forest Stands
Broadleaf
Silver birch (Betula pendula)	85	3
Oak (Quercus robur/pubescens/petraea)	115	12
Red Oak (Quercus rubra)	147	7
Aspen (Populus spp.)	211	6
European Ash (Fraxinus excelsior)	80	3
Black locust (Robinia pseudoacacia)	63	7
Willow (Salix spp.)	50	3
Eucalyptus (Eucalyptus spp.)	148	4
Conifer
Corsican Pine (Pinus nigra subsp. laricio)	70	6
Maritime Pine (Pinus pinaster)	103	7
Black Pine (Pinus nigra)	55	2
Silver Fir (Abies alba)	75	5
Douglas Fir (Pseudotsuga menziesii)	60	7

). In some species, identification was limited to the genus level because of the existence of cultivars (case of Aspen) and the difficulty involved in determining the exact species of Oak, Willow and Eucalyptus. We acquired a total of 1262 sample plots (named reference samples in the rest of the paper). Class distribution was moderately imbalanced reflecting the uneven distribution of species abundances in the forests. The number of samples varied from 50 (the minimum for Willow) to 211 (the maximum for Aspen). Conifers were less well represented with an average of 73 samples per class compared with 112 for broadleaf species.

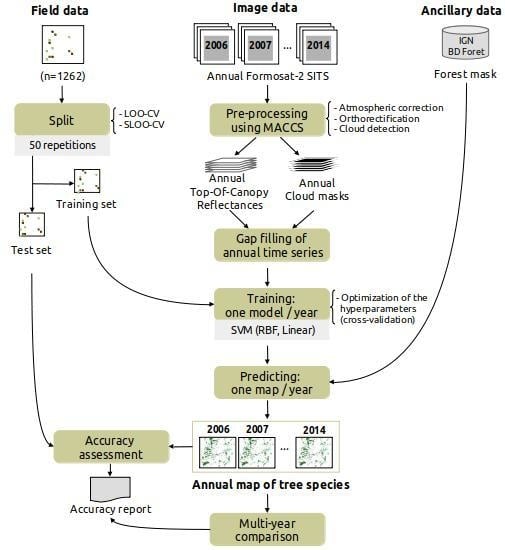
3. Classification Protocol

A global overview of the classification protocol applied on each Formosat-2 single-year time series is shown in Figure 3.

3.1. Pre-Processing

In this step, surface reflectance time series were produced from the Formosat-2 level 1A images using the MACCS (Multisensor Atmospheric Correction and Cloud Screening) processing chain developed by the CNES [44,45]. MACCS involved orthorectification, atmospheric correction, detection of clouds and cloud shadows, and reduction of topographic effects on illumination, based on multitemporal and multispectral criteria. Atmospheric correction relies on the estimation of aerosol optical thickness based on a spectro-temporal technique that minimizes (i) variations in surface reflectances between pixels acquired consecutive cloud-free images after correction and (ii) differences between the blue surface reflectance predicted from the red band (empirical relationship) and the blue surface reflectance obtained after correction [46]. Clouds are detected using a multitemporal approach that analyzes the increase in reflectance in the blue spectral band [45]. If high variation is observed, cloud is likely to be present. Based on this method, masks of clouds and related shadows are produced by MACCS for each image in the time series.

In the second step, SITS of each year were filtered using a linear gap-filling algorithm applied to each spectral band to remove noisy data (i.e., cloudy and shady pixels) and to retrieve their surface reflectance [47]. Invalid pixels were replaced by the interpolated values from the closest available valid pixels in the time series. Gap-filling was chosen for its simplicity and its previously demonstrated efficiency already demonstrated when time gaps between consecutive images are limited [48].

3.2. Training

Classification models were built using all spectral bands of each annual time series as predictors with exactly the same pixels for training and testing. We used the supervised SVM (Support Vector Machine) classifier [49] known to be the best approach in the case of small training data sets with respect to data dimensionality [50]. In this study, we selected the Radial Basis Function (RBF) kernel which is the most frequently used and has already been proven to be effective in the case of similar classification problems [51]. Hyperparameters including the regularization parameter (C) and the kernel bandwidth ($\gamma$) were tuned by cross-validation in a search space with the following settings: $C=$ {$0.01,0.1,\dots ,1^{10}$} and $\gamma =$ {$1^{-9},1^{-8},\dots ,1^3$}. A linear kernel was also tested for comparison with RBF. However, since the linear kernel performed worse, the results are not presented here. To account for imbalanced data and to prevent potential bias due to the dominant classes [52], the class weights in the SVM parameters were also modified. Weights were set inversely proportional to class frequencies. SVM was computed using the scikit-learn python library [53]. Vector of features were standardized (i.e., centering and scaling to unit variance) prior to training.

3.3. Estimating Prediction Errors by Spatial Cross-Validation

Because spatial autocorrelation between training and test sets may produce optimistic bias in assessments of classification performance [39,41,42], we used a spatial leave-one-out cross-validation (SLOO-CV) sampling strategy [54,55] to separate the training and test sets to guarantee full independence between them. In this approach, one reference sample is used as the test set and the remaining samples, non-spatially correlated with the test set, are used as the training set (Figure 4). This is repeated n times where n equals the number of samples. The n prediction results are then averaged to obtain an estimation of the prediction error. In our case, the test set was composed of one pixel of each class (i.e., a total of 13 pixels at each iteration) and the procedure was repeated 50 times, this being the number of reference samples of the lowest class size. We compared this splitting procedure with the classical non-spatial leave-one-out cross-validation strategy (LOO-CV) using the same training size per class as in SLOO-CV, by random undersampling. For year-to-year comparison, we also used the same training and test sets related to each sampling approach by setting the same random seed.

The spatial autocorrelation distance was estimated by computing the Moran’s Index from the pixels of forests in the SITS [56]. Moran’s I estimates the correlation between the value of a variable at one location and nearby observations. The index ranges from -1 (negative spatial autocorrelation) to +1 (positive spatial autocorrelation) with a value close to 0 in the absence of spatial autocorrelation (random spatial distribution). More formally, the Moran’s I is defined as the ratio of the covariance between neighborhood pixels and the variance of the entire image:

$$I\left(d\right)=\frac{n}{S_0}\frac{\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}(x_i-\overline{x})(x_j-\overline{x})}{\sum _{i=1}^n{(x_i-\overline{x})}^2}$$

(1)

where, in our case, $x_i$ is the pixel value of x (a spectral band of the SITS for pixels of forests) at location i, $x_j$ is the pixel value of x at location j (a nearby pixel of forest of i), $\overline{x}$ is the average value of x, n is the number of pixels of forests in the image, $w_{i,j}$ is the weight equals to 1 if pixel j is within distance d of pixel i, otherwise $w_{i,j}=0$, and $S_0$ the sum of all $w_{i,j}$’s:

$$S_0=\sum _{i=1}^n\sum _{j=1}^n{w}_{i,j}$$

(2)

In this study, Moran’s I was computed for each spectral band of each year, for neighborhoods (lags) varying from 1 to 100 pixels (i.e., from 8 m to 800 m). Based on correlograms, we evaluated the distance between nearby pixels for which Moran’s I equals 0.2, considering the potential effect of spatial autocorrelation as not significantly different from the thresold value of Moran’s I [57]. Then, the median distance was calculated for each spectral band, taking all the dates of one year into account (Figure 5). This was done for each year. Finally, the average value of the median distance of each year was kept in the spatial cross-validation procedure to split the training and test sets. This average value was estimated to be 340 m (i.e., 42 pixels).

3.4. Accuracy Assessment of One-Year Classifications and Comparison

The results of the classifications were assessed according to the confusion matrix based on Overall Accuracy (OA) and the F1 score (i.e., the harmonic mean of precision and recall varying from 0 for the worst case to 1 for perfect classification), errors of omission and errors of commission. A Wilcoxon signed-rank test was used to determine if the difference in accuracy between annual classifications and sampling strategies (LOO-CV vs SLOO-CV) was statistically significant.

Classifications were also compared spatially to highlight instability between years. A map of uncertainty was produced by computing the number of agreements between the one-year classifications (i.e., the modal value related to the class with the highest frequency) for each pixel. Additionally, the distribution of this uncertainty was examined per class using either all the predicted pixels or only the reference samples. Finally, the maps were visually inspected to identify problem areas and to better understand the errors with the help of field knowledge. The maps shown in results section were produced using the SLOO-CV.

4. Results

4.1. Overall Statistical Performances

The classification performances for each year are presented in

Table 2. Accuracy report of spatial leave-one-out cross-validation (SLOO-CV) sampling strategy and leave-one-out cross-validation (LOO-CV) for each single-year classification based on OA statistics. The 2006bis time series only includes cloud-free images of 2006. The average percentage of cloud coverage was estimated by computing for each species the number of time each reference sample was affected by clouds (detected from the MACCS processing chain).

	2006	2006bis	2007	2008	2009	2010	2011	2012	2013	2014
Classification accuracy (average Overall Accuracy ± standard deviation)
SLOO-CV	0.52 ± 0.13	0.57 ± 0.15	0.48 ± 0.12	0.57 ± 0.10	0.55 ± 0.11	0.56 ± 0.12	0.55 ± 0.11	0.58 ± 0.14	0.60 ± 0.11	0.58 ± 0.11
LOO-CV	1.00 ± 0.02	0.99 ± 0.03	0.99 ± 0.02	0.98 ± 0.04	0.99 ± 0.03	0.98 ± 0.03	0.97 ± 0.04	0.98 ± 0.04	0.99 ± 0.02	1.00 ± 0.02
Characteristics of each SITS
Number of images	43	20	15	11	16	14	12	13	17	15
Images in spring	13	4	2	1	2	3	4	3	3	5
Images in autumn	10	6	4	4	3	4	4	2	4	4
Cloud coverage	25%	0%	12%	5%	4%	3%	2%	0%	1%	0%

. Generally speaking, the performances were similar between the years but very different between sampling strategies (SLOO-CV vs LOO-CV) in a given year.

When prediction errors were estimated by spatial cross-validation (SLOO-CV), the average OA varied from 0.48 in 2007 to 0.60 in 2013 with high variability in the results (average standard deviation of 0.12). No significant differences were observed between the years 2008–2012, 2012–2014 and between 2006 and 2007 which were the cloudiest SITS ($p<0.05$; Wilcoxon signed-rank test statistic; see Appendix B for statistical details). For the year 2006, when cloudy images were removed from the SITS (i.e., using the 2006bis dataset), the classification was improved, the performance was similar to that in the other years (average OA = 0.57). The best classification was obtained using the 2013 time series (average OA = 0.60).

When accuracy was computed using the standard leave-one-out cross-validation (LOO-CV), prediction errors were very low compared to when SLOO-CV was used, suggesting a high optimistic bias in the evaluation. The average OA varied from 0.97 in 2011 to 1.00 in 2006 and 2014 with a standard deviation close to zero. The cloudiest years (2006 and 2007) did not differ significantly in performance from the other years in most cases (Appendix B). These results contradict the previous ones: while the year 2007 was the worst with the SLOO-CV, with LOO-CV it had the second best score.

In the following sections, we only detail the results based on the SLOO-CV strategy since it best reflects the true performance of the classifications.

4.2. Accuracy per Species

In most cases, whatever the year, broadleaf tree species were better discriminated than conifers (Figure 6). The highest performances were obtained for monospecific plantations of Red oak (average F1 score = 87%) and Willow (average F1 score = 86%). Aspen was also detected with good accuracy (average F1 score = 68%). Conversely, some species were difficult to identify, including European ash (average F1 score = 26%) and Silver birch (average F1 score = 36%) except in the years 2010 and 2013.

High confusion rates were obtained for conifer tree species. Black pine was the worst class with a F1 score close to zero, except in 2014 (F1 score = 62%). Maritime pines were generally better discriminated but the performances remained low (average F1 score = 40%). The best agreement was obtained for Silver fir (average F1 score = 50%) which reached its best score (average F1 score = 81%) in the year 2010.

On average, the year 2013 was the best, mainly because of a high score for Silver birch compared to the other years. Year 2007 was the least accurate. Higher performance disparity was observed from one year to another for most species, except Red oak and Willow.

4.3. Confusion between Species

Generally, when errors occurred, the broadleaf tree species were confused with each other as well as with conifers. The main source of omissions for Silver birch was mispredictions as Oak which, in turn, was confused with European ash but also with Black locust and with some pines (see the confusion matrix for the year 2013 in Figure 7, for example). Red oak was the subject of very little confusion. High rates of omissions were observed for European ash with misclassifications as Oak, Aspen and Black locust. Under-detection was also observed for the evergreen Eucalyptus plantations due to confusion with Willow. In conifer species, the errors mainly appeared between species of Pine but also between Pine and Douglas fir.

Confusions between species were similar from one year to another but the commission and omission errors rates varied and accuracy was very low for some species (Figure 8).

4.4. Spatial Agreement between Years

As revealed by the map of the modal class values, Oak was the most representative species in the study region, especially in the small forests, which is consistent with our field observations (Appendix A). Conifers and plantations of broadleaf species were less frequent but pixels of the same class appear to be grouped in homogeneous stands, as expected.

When spatial uncertainty was analyzed using the map of agreements between the one-year classifications, good stability was observed in the monospecific tree plantations of broadleaf species (Figure 9). The stands composed of Aspen, Red oak, and Eucalyptus were clearly differentiated. In contrast, in complex forests including a mix of different species, disagreements between annual classifications were higher, as suggested by the previous statistical assessment. An example is given in Figure 10 showing a mix forest composed of conifers (mainly Black pine but also Douglas fir and Silver fir) and deciduous species (mainly Oak and Silver birch). There was considerable confusions between conifer species from one year to another (low agreement). The extent of Silver birch areas was also highly variable. In this forest, the dominant species were rather well-identified but their exact location was inaccurate at the pixel level.

Significant disagreements between the classifications were also observed in other contexts, especially in thin riparian forests and forest edges where species composition and diversity is high, with lots of species unsampled (Figure 9). This was also true in low density forest stands, for which confusions appeared with the understory vegetation. Finally, disagreements were also observed in areas very affected by clouds and cloud shadows.

5. Discussion

In this study, an archive of Formosat-2 time series was used to classify tree species in temperate forests in nine consecutive years. Each classification was validated using the same spatial leave-one-out cross-validation approach to remove the test samples that were spatially correlated with the training samples. To our knowledge, this is the first study to examine the stability of predictions from one year to another using dense SITS of high spatial resolution with spatially independent validation data. The present study is a first attempt to assess the robustness of tree species discrimination in multiple years and to better understand the drivers that affect classification performances.

5.1. Effect of Spatial Autocorrelation: The SLOO-CV Strategy as a Standard

Our results revealed a strong positive bias in validation based on the usual LOO-CV strategy for splitting reference data. This bias was already suspected in our previous studies when we used stratified-k-fold but was not quantified [38,58]. Regarding the importance of the overestimation in the classification accuracy ($\Delta$OA > 0.4 between LOO and SLOO-CV), the use of spatially independent data for validation should no longer be an option but wherever possible, a requirement, in agreement with the recommendation of [9].

Spatial autocorrelation in the reference data has long been known to affect the classification and accuracy assessment [39,40,59,60]. Different sampling strategies for data splitting have already been studied in the literature including spatial [42,55,61,62] and aspatial approaches [61,63,64,65]. Although the spatial sampling approach is recommended to reduce the spatial autocorrelation effect, an aspatial (i.e., random, systematic or stratified) sampling strategy assuming independence between training and test sets is usually used in remote sensing analyses for the sake of simplicity [65].

In this study, the SLOO-CV strategy was used to estimate an unbiased prediction performance, similar to used in [54]. We measured the spatial dependence between nearby pixels of forests explicitly, using the Moran’s I, as in [66], and we separated training and validation samples that were located geographically too close to one another. In other studies, spatial partitioning was achieved differently, based on k-means clustering [42,67] or on the definition of patches [68], or blocks related to the spatial structure [62]. In these approaches, the spatial dependence between training and test sets is supposed to be removed but this is not verified. Whatever the spatial sampling method used, all the studies demonstrated larger errors in predictions with lower spatial autocorrelation between training and test sets, as we observed here. The absence of independence between training and testing samples thus provides an inflated estimate of classification performances as confirmed by our results.

An important point to note is that we guaranteed complete independence between the training and test sets but not among the training samples. Thus, spatial autocorrelation still persisted in the training set. Compared to LOO-CV, the SLOO-CV strategy provides a statistical estimate of accuracy that fits the quality of the map product better (and hence predictive performance) but in terms of predictions, the results of classification results are similar. This is illustrated by the number of agreements between the annual classifications for both LOO-CV and SLOO-CV (Figure 11). With the exception of some classes (e.g., Maritime and Black pine), the distribution of agreements per class of species is rather similar.

5.2. Effect of the Size of the Reference Sample

The size of the training sample dataset is known to be a key factor affecting both classification accuracy and predictive performance [59,69]. In practice, it is hard to adequately judge the optimal training set size which depend on several factors such as the number of features, the degree of imbalance in class distribution, and the machine learning algorithm. In this study, we used the SVM classifier, which is known to be less sensitive to sample size since the decision boundaries rely on only a few support vectors. We also adjusted class weights to avoid bias due to the uneven distribution of tree species. Nevertheless, we obtained a slightly significant positive correlation (r = 0.52; p-value = 0.06) between the average number of pixels used for training (see Appendix D) and the average F1 score obtained for each species (including all the years), suggesting a potential effect of training set size on accuracy. We also observed that the least well-identified species were those with a limited number of forest stands (only three for Silver birch, European ash and Black pine). For these small classes, the presence of noise on the data (under detected clouds or cloud shadows under-detected, see below) may have a greater negative impact on their discrimination. However, Willow is an exception, as it was the least populated species with only 21 samples for training and a total of three forest stands but obtained the second highest F1 score (average = 0.86) behind Red oak (average = 0.87) with 118 samples (Appendix D).

More generally, due to the complexity of the learning problem (i.e., partial overlapping between spectro-temporal signatures of species in the feature space), increasing the size of the training sample and reducing the degree of imbalance in class distribution should improve the predictive performance [70]. In a recent study, Bolyn et al. [33] obtained a high degree of accuracy (OA = 88.5%) when they classified 11 forest classes (including seven tree species) in the entire Belgian Ardenne ecoregion with only two Sentinel-2 dates. Although this statistical performance may be partially inflated by spatial autocorrelation, this greater accuracy could also be explained by the large sample size (from 2589 to 7068 pixels for each class with a minimum of 31 forest stands and a maximum of 64). An equivalent level of performance (OA = 88.2%) was obtained by [34] when they identified five tree species in a forest in central Sweden using four S2 images acquired from spring to autumn. However, in their case study, the sample size was very close to ours (from 27 to 98 pixels per species). Spatial overfitting is suspected, as in our previous works [38,58].

5.3. Effect of Clouds and Cloud Shadows

When we compared the stability of predictions from one year to another (i.e., the map of agreements between the annual classifications) with the number of times the pixels were affected by clouds or cloud shadows, we found no significant correlation. This indicates that disagreements between the classifications can not be attributed to this factor. We observed that the years most affected by clouds (2006 and 2007) had the lowest average OA values (52% and 48% respectively, see Table 2). However, for the other years, the F1 score per species was not always consistent with the extent of cloud coverage. For instance, in 2008, 11% of the reference pixels for Oak were affected by clouds (Appendix C) but the F1 score was the highest of all the years. This suggests that when clouds and cloud shadows are detected by the MACCS processing chain, the gap-filling approach is appropriate to correct noisy pixels. This procedure is currently used in the French production center THEIA (https://theia.cnes.fr) for Landsat, VEN$\mathsf{\mu }$S and Sentinel-2 level2A products.

An in-depth visual analysis of the map products in fact revealed that misdetections of clouds and cloud shadows had a major effect on classification performances. When the forests were partially affected by clouds and cloud shadows or when these were under detected (which is what happened in the case of slight fog), spectral signatures were skewed and confusion between species was likely. This issue is illustrated in Figure 12 which shows changes in the reflectance values of an Oak pixel in 2006. On most of the dates, the pixel was free of clouds and shadows (green dots). In some cases, clouds or cloud shadows were found and the pixel values were gap-filled by linear interpolation (orange dots). But on certain dates, clouds or cloud shadows were not detected (red dots) and this influences the spectro-temporal signature. These dates had erroneous values but also had a negative impact on nearby gap-filled values since the dates are considered to be valid (e.g., see the 10th image in Figure 12). Another example showing an erroneous spatial pattern in a forest stand due to undetected clouds is provided in Appendix A Figure A3. This noise may influence the training step through the addition of inadequate support vectors, as well as the validation step, if the reference pixel to be tested is impacted by noise but the training pixels are not.

An alternative to the gap-filling approach to reduce noise could be the use of smoothing methods applied to the whole time series and not only to a limited temporal window (i.e., the cloudy and shady pixels). Non-parametric methods such as Whittaker smoother [71] or splines [72] may be appropriated. Another way to limit the effect of noise could be reducing the number of features [73]. Limiting the number of features in the classification protocol could help remove noise but also prevent the Hughes phenomenon [74] (i.e., a decrease in accuracy with the addition of new features after an initial increase). In theory, the Hughes effect should not be observed with the SVM classifier which is robust to the dimensionality of data [75]. However, a previous study demonstrated a positive role of feature selection on classification results with SVM, particularly when the training set used is small [76].

5.4. Effect of the Available Dates in the SITS

We hypothesized that time series data improve the identification of tree species compared to the use of only one date or a couple of images due to phenological differences in spring or autumn. Using several dates should be better than using one date, whatever the year, as demonstrated in [30,31,34]. However, because of the variation in the dates available from one year to another, the differences in cloud and shadow contamination, and the potential Hughes effect, it is difficult to give a clear answer concerning the most appropriate time windows to separate species. When we examine the relationships between the classification performances and the number of dates acquired during the key seasons, we find no evidence of a positive effect. For example, classification accuracy in the year 2008 was statistically equivalent to that in the year 2014 when there was comparable cloud coverage (<5%) whereas we only had one available image in spring 2008 versus five in 2014. Similarly, classification performance in the year 2009 was statistically identical to that in other years including in 2006bis. However, in autumn 2009, no images were available from end of October to the middle of December and only a very limited number of images were available in spring compared to 2006bis which had four dates in spring and six dates in autumn (Figure 2).

In order to better evaluate the most relevant dates for classification and to assess the sensitivity of our results to the Hughes effect, an additional analysis was carried out using a feature selection approach following the SLOO-CV strategy. Feature selection was based on the simple Sequential Forward Selection (SFS) algorithm which adds at each iteration, the most important feature (sensu OA) in the pool of selected ones, starting with an empty set [77]. Each feature is permanently conserved after selection and the process is repeated until all the features are included. Here, the feature selection approach was applied for each year, using all the spectral bands of the available dates. However, to reduce the computation time, we considered as a feature a single-date acquisition composed of four spectral bands.

Globally, this analysis confirmed the difficulty to draw robust conclusions about the tangible contribution of seasonal variations in species discrimination. The most important dates were highly variable from one year to another because of the irregular acquisition dates. For instance, compared to 2008, the maximum classification accuracy of 2011 (OA = 0.62) was statistically equivalent, for the same number of dates (5 dates) after feature selection. However, the image ranking was quite different with more dates selected in autumn in 2008 compared to 2011 (Figure 13a,b). In 2013, the first two most important dates enabling to reach a similar level of accuracy (OA ≈ 0.62) were acquired in winter and summer which is still different in 2014 (Figure 13c,d; see Appendix E for full results). What appears to be constant in this additional analysis is the limited number of dates (around five) to reach maximum accuracy and the decrease in accuracy using all the dates. The identification of tree species is improved with the use of multitemporal images compared to single-date image but in a most effective way when feature selection is applied before training. The use of fewer features that contain the maximum discrimination information about the tree species classes is better than the use of all the features of which many of them could be correlated or irrelevant because of noise. These results confirms that the Hughes effect can occur using SVM, as already observed by [76]. This is also in line with the Zhu and Liu’s recommendations of selecting the most discriminative features before classifying forest types using dense time series [24].

In a study, a combination of three aerial images acquired in spring (March 17th), summer (July 16th) and autumn (October 27th) provided the highest classification accuracy compared to all possible combinations based on five dates [30]. When only one image was selected, autumn appeared to be the best period to distinguish between common Oak, English Oak, Field Maple, Silver birch, Aspen and small-leaved Elm. In other recent studies based on Sentinel-2 data, the optimal single date was found in May [33,34]. The same observation was made when discrimating deciduous tree species in a multitemporal image dataset acquired with an unmanned aerial system [31]. When more images were combined, the best datasets included data acquired in different seasons (spring, early summer and autumn) in accordance with [30].

5.5. Differences between Species

We found more difficulty to separate conifers than broadleaf species as previously highlighted in other studies when multitemporal data are used [13,26,34,38,78]. Seasonal changes are less pronounced which induces higher overlapping between spectro-temporal profiles. Pine species were the harder to identified (in particular Corsican and Black pines). Among broadleaf species, European Ash and Silver birch were the most confused (contrary to [13]). The best agreements were obtained for Red Oak, Eucalyptus, Willow and Aspen, in line with [31] for the latter species.

The evergreen phenology of Eucalyptus explains its high rate of agreements among 9 years despite a medium F1-score (average of all years OA = 65%). Because of differences in morphological and anatomical traits, optical properties also differ from those of conifers. The Red oak phenology is also specific, in particular in autumn when leaves turn red due to the production of anthocyanins. This gives a spectral characteristic which help to recognize them among the other species. For Willow, stands are located in well-suited humid areas sometimes waterlogged. The variable moisture conditions associated with a partially recovering canopy provide them a weaker reflectance in the near-infrared band compared to the other broadleaf species which may explain the good classification accuracy. For other species that cannot easily be separated, various factors may be involved, in addition to close spectral signatures. Forest managing practice is one of them. Stand age, density and the existence of understory vegetation are others. Spectral disparity for a given species (intra-species variability) may also influence the classification [31].

6. Conclusions

This study based on temperate forests in France is the first to explore the stability of tree species classification over nine consecutive years using dense high spatial resolution SITS with spatially uncorrelated validation data. The study was based on surface reflectance products derived from Formosat-2 optical time series acquired at irregular intervals from 2006 to 2014. Despite close statistical results in terms of classification accuracy, we observed high spatial disparities from one year to the next reflecting the moderate ability to predict tree species at the pixel level because of various disturbing factors.

Based on our findings, several conclusions can be drawn:

• Spatial autocorrelation within validation data drastically overestimates the classification accuracy. In our context, an average optimistic bias of 0.4 of OA is observed when spatial dependence remained (LOO-CV strategy vs SLOO-CV). In further studies, we recommend adapting the data-splitting procedure to systematically reduce or eliminate spatial autocorrelation in the validation set in order to provide more robust conclusions about the true predictive performance.
• Noise in the time series (i.e., undetected clouds and shadows) affects the SVM based classification performances. Despite accurate masks of clouds and shadows and a gap-filling approach to correct invalid pixels, residual noise impacts the learning and prediction processes. Feature selection is a good option to ignore noisy data, reduce data dimension, and to find the optimal subset of images for classification. There is a clear benefit (+0.08 of OA in average) of using fewer images containing the maximum discrimination information about the tree species classes.
• The use of multitemporal images improves the tree species discrimination compared to single-date image. However, there is no clear evidence that the positive effect is really due to phenological differences between species. The most important dates varied from one year to another with no strong preference for images acquired at the key seasons.
• The monospecific broadleaf plantations of Aspen, Red Oak and Eucalyptus are the easiest to classify. Conifers are the most difficult. The lowest accuracy was obtained for Silver birch, European ash and Black pines for which only a few forest stands were available.

Perspectives of this study are twofold. The first one is the use of S2 time series to confirm the results and assess the contribution of additional spectral bands such as the red-edge to separate tree species for the same in situ dataset and area. With its 5-day revisit time, S2 provides many more data in one year. These new time series should help better identify the best combination of multitemporal images and check that the combination is consistent with phenological events of the tree species concerned. Work is in progress to collect ground phenological observations on the study site. S2 also offers the possibility to work at a larger scale and will thus give us more reference pixels to reduce the bias due to the spatial autocorrelation. The second is related to the Formosat-2 time series. Annual datasets could be combined to reconstruct a synthesized multiyear time series based on all cloud-free images to combine all the phenological events of the species into one representative year.

In order to reproduce this study or to have tree species ground references suitable for remote sensing, our reference samples are publicly available at Zenodo, the Open Science platform at the CERN Data (https://doi.org/10.5281/zenodo.2581400). An interactive web version of the predicted species map using the 10 SITS with the Spatial Leave-One-Out cross-validation method (SLOO-CV) is available online (https://dynafor1201.github.io/publications/maps/treespeciesformosat2/).