Multi-Scale Association between Vegetation Growth and Climate in India: A Wavelet Analysis Approach
Abstract
:1. Introduction
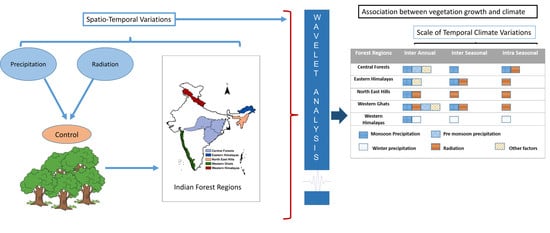
2. Materials and Methods
2.1. Study Region
2.2. Datasets
2.3. Quality Filter
2.4. Wavelet Analysis
3. Results and Discussions
3.1. Multi-Scale Temporal Variation
3.2. Wavelet Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- India State of Forest Report. 2017. Available online: http://fsi.nic.in/isfr2017/isfr-forest-cover-2017.pdf (accessed on 28 March 2018).
- Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; da Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Mooley, D.A.; Parthasarathy, B. Fluctuations in All-India summer monsoon rainfall during 1871–1978. Clim. Chang. 1984, 6, 287–301. [Google Scholar] [CrossRef]
- Pathak, A.; Ghosh, S.; Martinez, J.A.; Dominguez, F.; Kumar, P. Role of Oceanic and Land Moisture Sources and Transport in the Seasonal and Interannual Variability of Summer Monsoon in India. J. Clim. 2017, 30, 1839–1859. [Google Scholar] [CrossRef]
- Kripalani, R.H.; Kumar, P. Northeast monsoon rainfall variability over south peninsular India vis-à-vis the Indian Ocean dipole mode. Int. J. Climatol. 2004, 24, 1267–1282. [Google Scholar] [CrossRef]
- Rajeevan, M.; Unnikrishnan, C.K.; Bhate, J.; Niranjan Kumar, K.; Sreekala, P.P. Northeast monsoon over India: Variability and prediction. Meteorol. Appl. 2012, 19, 226–236. [Google Scholar] [CrossRef]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Singh, R.B.; Mal, S. Trends and variability of monsoon and other rainfall seasons in Western Himalaya, India. Atmos. Sci. Lett. 2014, 15, 218–226. [Google Scholar] [CrossRef]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef]
- Zhang, X.; Tarpley, D.; Sullivan, J.T. Diverse responses of vegetation phenology to a warming climate. Geophys. Res. Lett. 2007, 34, L19405. [Google Scholar] [CrossRef]
- Justiniano, M.J.; Fredericksen, T.S. Phenology of Tree Species in Bolivian Dry Forests. Biotropica 2000, 32, 276–281. [Google Scholar] [CrossRef]
- Kramer, K.; Leinonen, I.; Loustau, D. The importance of phenology for the evaluation of impact of climate change on growth of boreal, temperate and Mediterranean forests ecosystems: An overview. Int. J. Biometeorol. 2000, 44, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B. Phenology of tropical forests: Patterns, causes, and consequences. Can. J. Bot. 1995, 73, 164–174. [Google Scholar] [CrossRef]
- Wright, S.J. Seasonal drought, soil fertility and the species density of tropical forest plant communities. Trends Ecol. Evol. 1992, 7, 260–263. [Google Scholar] [CrossRef]
- Schimper, A.F.W. Plant-Geography upon a Physiological Basis; Schimper, A.F.W., Ed.; 1856–1901: Free Download, Borrow, and Streaming: Internet Archive; Clarendon Press: Oxford, UK, 1903; Available online: https://archive.org/details/plantgeographyup00schi (accessed on 26 April 2018).
- Gentry, A.H. Changes in Plant Community Diversity and Floristic Composition on Environmental and Geographical Gradients. Ann. Mo. Bot. Gard. 1988, 75, 1–34. Available online: http://www.jstor.org/stable/2399464 (accessed on 26 April 2018). [CrossRef]
- Comita, L.S.; Queenborough, S.A.; Murphy, S.J.; Eck, J.L.; Xu, K.; Krishnadas, M.; Beckman, N.; Zhu, Y. Testing predictions of the Janzen-Connell hypothesis: A meta-analysis of experimental evidence for distance- and density-dependent seed and seedling survival. J. Ecol. 2014, 102, 845–856. [Google Scholar] [CrossRef]
- Terborgh, J. Enemies Maintain Hyperdiverse Tropical Forests. Am. Nat. 2012, 179, 303–314. [Google Scholar] [CrossRef]
- Guan, K.; Pan, M.; Li, H.; Wolf, A.; Wu, J.; Medvigy, D.; Caylor, K.K.; Sheffield, J.; Wood, E.F.; Malhi, Y. Photosynthetic seasonality of global tropical forests constrained by hydroclimate. Nat. Geosci. 2015, 8, 284–289. [Google Scholar] [CrossRef]
- Saleska, S.R.; Didan, K.; Huete, A.R.; da Rocha, H.R. Amazon forests green-up during 2005 drought. Science 2007, 318, 612. [Google Scholar] [CrossRef]
- Wagner, F.H.; Hérault, B.; Rossi, V.; Hilker, T.; Maeda, E.E.; Sanchez, A.; Lyapustin, A.I.; Galvão, L.S.; Wang, Y.; Aragao, L.E. Climate drivers of the Amazon forest greening. PLoS ONE 2017, 12, e0180932. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Prasad, V.K.; Badarinath, K.V.S.; Eaturu, A. Effects of precipitation, temperature and topographic parameters on evergreen vegetation greenery in the Western Ghats, India. Int. J. Climatol. 2008, 28, 1807–1819. [Google Scholar] [CrossRef]
- Prasad, V.K.; Anuradha, E.; Badarinath, K.V.S. Climatic controls of vegetation vigor in four contrasting forest types of India—evaluation from National Oceanic and Atmospheric Administration’s Advanced Very High Resolution Radiometer datasets (1990–2000). Int. J. Biometeorol. 2005, 50, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Krishna Prasad, V.; Badarinath, K.V.S.; Eaturu, A. Spatial patterns of vegetation phenology metrics and related climatic controls of eight contrasting forest types in India—Analysis from remote sensing datasets. Theor. Appl. Climatol. 2007, 89, 95–107. [Google Scholar] [CrossRef]
- Furon, A.C.; Wagner-Riddle, C.; Smith, C.R.; Warland, J.S. Wavelet analysis of wintertime and spring thaw CO2 and N2O fluxes from agricultural fields. Agric. For. Meteorol. 2008, 148, 1305–1317. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J.; Holschneider, M. Nonstationary Gaussian processes in wavelet domain: Synthesis, estimation, and significance testing. Phys. Rev. E 2007, 75, 016707. [Google Scholar] [CrossRef] [PubMed]
- Torrence, C.; Compo, G.P.; Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. A multicomponent decomposition of spatial rainfall fields: 1. Segregation of large- and small-scale features using wavelet transforms. Water Resour. Res. 1993, 29, 2515–2532. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Szilagyi, J.; Parlange, M.B.; Katul, G.G.; Albertson, J.D. An objective method for determining principal time scales of coherent eddy structures using orthonormal wavelets. Adv. Water Resour. 1999, 22, 561–566. [Google Scholar] [CrossRef]
- Takeuchi, N.; Narita, K.I.; Goto, Y. Wavelet analysis of meteorological variables under winter thunderclouds over the Japan Sea. J. Geophys. Res. 1994, 99, 10751. [Google Scholar] [CrossRef]
- Turner, B.J.; Leclerc, M.Y.; Gauthier, M.; Moore, K.E.; Fitzjarrald, D.R. Identification of turbulence structures above a forest canopy using a wavelet transform. J. Geophys. Res. Atmos. 1994, 99, 1919–1926. [Google Scholar] [CrossRef]
- Venugopal, V.; Foufoula-Georgiou, E. Energy decomposition of rainfall in the time-frequency-scale domain using wavelet packets. J. Hydrol. 1996, 187, 3–27. [Google Scholar] [CrossRef]
- Venugopal, V.; Roux, S.G.; Foufoula-Georgiou, E.; Arneodo, A. Revisiting multifractality of high-resolution temporal rainfall using a wavelet-based formalism. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, V.; Foufoula-Georgiou, E.; Sapozhnikov, V. Evidence of dynamic scaling in space-time rainfall. J. Geophys. Res. Atmos. 1999, 104, 31599–31610. [Google Scholar] [CrossRef]
- Flinchem, E.P.; Jay, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods. Estuar. Coast. Shelf Sci. 2000, 51, 177–200. [Google Scholar] [CrossRef] [Green Version]
- Percival, D.B.; Mofjeld, H.O. Analysis of Subtidal Coastal Sea Level Fluctuations Using Wavelets. J. Am. Stat. Assoc. 1997, 92, 868–880. [Google Scholar] [CrossRef]
- Guyodo, Y.; Gaillot, P.; Channell, J.E. Wavelet analysis of relative geomagnetic paleointensity at ODP Site 983. Earth Planet. Sci. Lett. 2000, 184, 109–123. [Google Scholar] [CrossRef]
- Yokoyama, Y.; Yamazaki, T. Geomagnetic paleointensity variation with a 100 kyr quasi-period. Earth Planet. Sci. Lett. 2000, 181, 7–14. [Google Scholar] [CrossRef]
- Martínez, B.; Gilabert, M.A. Vegetation dynamics from NDVI time series analysis using the wavelet transform. Remote Sens. Environ. 2009, 113, 1823–1842. [Google Scholar] [CrossRef]
- Roy, P.S.; Behera, M.D.; Murthy, M.S.R.; Roy, A.; Singh, S.; Kushwaha, S.P.S.; Jha, C.S.; Sudhakar, S.; Joshi, P.K.; Reddy, C.S.; et al. New vegetation type map of India prepared using satellite remote sensing: Comparison with global vegetation maps and utilities. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 142–159. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The national solar radiation data base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series). Available online: http://vip.arizona.edu (accessed on 28 March 2018).
- Xiao, X.; Zhang, Q.; Saleska, S.; Hutyra, L.; De Camargo, P.; Wofsy, S.; Frolking, S.; Boles, S.; Keller, M.; Moore III, B. Satellite-based modeling of gross primary production in a seasonally moist tropical evergreen forest. Remote Sens. Environ. 2005, 94, 105–122. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Chatfield, C. Introduction to Multivariate Analysis; Routledge: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Liu, P.C. Wavelet Spectrum Analysis and Ocean Wind Waves. Wavelet Anal. Its Appl. 1994, 4, 151–166. [Google Scholar] [CrossRef]
- Bradshaw, G.A.; McIntosh, B.A. Detecting climate-induced patterns using wavelet analysis. Environ. Pollut. 1994, 83, 135–142. [Google Scholar] [CrossRef]
- Labat, D. Cross wavelet analyses of annual continental freshwater discharge and selected climate indices. J. Hydrol. 2010, 385, 269–278. [Google Scholar] [CrossRef]
- Yu, H.-L.; Lin, Y.-C. Analysis of space–time non-stationary patterns of rainfall–groundwater interactions by integrating empirical orthogonal function and cross wavelet transform methods. J. Hydrol. 2015, 525, 585–597. [Google Scholar] [CrossRef]
- Liu, Q.; Hao, Y.; Stebler, E.; Tanaka, N.; Zou, C.B. Impact of Plant Functional Types on Coherence Between Precipitation and Soil Moisture: A Wavelet Analysis. Geophys. Res. Lett. 2017, 44, 12197–12207. [Google Scholar] [CrossRef] [Green Version]
- Shukla, R.P.; Ramakrishnan, P.S. Phenology of Trees in a Sub-Tropical Humid Forest in North-Eastern India*. Available online: https://link.springer.com/content/pdf/10.1007%2FBF00052764.pdf (accessed on 15 May 2018).
- Liu, C.; Allan, R.P. Observed and simulated precipitation responses in wet and dry regions 1850–2100. Environ. Res. Lett. 2013, 8, 034002. [Google Scholar] [CrossRef]







| Forest Regions | Inter Annual | Inter Seasonal | Intra Seasonal |
|---|---|---|---|
| Central Forests |  |  |  |
| Eastern Himalayas |  |  |  |
| North East Hills |  |  |  |
| Western Ghats |  |  |  |
| Western Himalayas |  |  |  |
 | Monsoon Precipitation |  | Pre monsoon precipitation |
 | Winter precipitation |  | Radiation |
 | Other factors |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebastian, D.E.; Ganguly, S.; Krishnaswamy, J.; Duffy, K.; Nemani, R.; Ghosh, S. Multi-Scale Association between Vegetation Growth and Climate in India: A Wavelet Analysis Approach. Remote Sens. 2019, 11, 2703. https://doi.org/10.3390/rs11222703
Sebastian DE, Ganguly S, Krishnaswamy J, Duffy K, Nemani R, Ghosh S. Multi-Scale Association between Vegetation Growth and Climate in India: A Wavelet Analysis Approach. Remote Sensing. 2019; 11(22):2703. https://doi.org/10.3390/rs11222703
Chicago/Turabian StyleSebastian, Dawn Emil, Sangram Ganguly, Jagdish Krishnaswamy, Kate Duffy, Ramakrishna Nemani, and Subimal Ghosh. 2019. "Multi-Scale Association between Vegetation Growth and Climate in India: A Wavelet Analysis Approach" Remote Sensing 11, no. 22: 2703. https://doi.org/10.3390/rs11222703
APA StyleSebastian, D. E., Ganguly, S., Krishnaswamy, J., Duffy, K., Nemani, R., & Ghosh, S. (2019). Multi-Scale Association between Vegetation Growth and Climate in India: A Wavelet Analysis Approach. Remote Sensing, 11(22), 2703. https://doi.org/10.3390/rs11222703