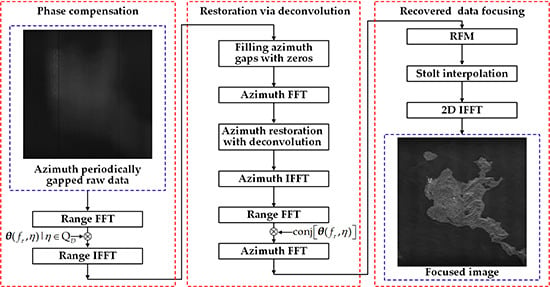
The proposed method for obtaining a focused image with deconvolution is described in this section. The phase compensation function, the restoration via deconvolution, a brief introduction of the RMA, and the procedure of the proposed method are presented.
2.1. Phase Compensation Function
Deconvolution can be regarded as a linear inverse problem. It is beneficial to solve linear inverse problems in a sparser domain [
33]. In this case, it is significant to process the azimuth periodically gapped raw data in a sparser domain. In
Section 2.1, a phase compensation function is designed to match the azimuth periodically gapped raw data in the range frequency domain. The phase compensation is implemented on raw data to remove modulation in the range direction and reduce most modulation in the azimuth direction. The data are compressed along the range direction in the range time domain due to the removal of range modulation. Moreover, the data are coarsely compressed along the azimuth direction in the azimuth frequency domain because of the reduction of the azimuth modulation. The azimuth frequency domain is also known as the Doppler domain. Therefore, the data are coarsely compressed in the range of the Doppler domain along both the range and azimuth direction after phase compensation. In other words, the energy of the data is more concentrated in the range of the Doppler domain after phase compensation. As a result, the gapped data become sparser in the range of the Doppler domain. Consequently, it is proper to restore the gapped data in the range of the Doppler domain after phase compensation. The description of the phase compensation function is derived and presented in this part.
In this paper, SAR is assumed to emit a pulse chirp signal and move with a uniform linear motion. After demodulation to its baseband, the echo data of a single point can be described by the range time
τ and azimuth time
η as below:
In Equation (1), the amplitude factors are neglected. wr is the range envelope, and wa is the azimuth envelope. The velocity of light is denoted as c. The range frequency modulation rate is denoted as Kr. R(η) is the slant range between the target and radar at η, f0 is the carrier frequency, and j is the imaginary unit. The complete SAR raw dataset is defined as a matrix with the size of Nr × Na. The complete SAR raw data have Nr and Na sampling points in the range and azimuth directions, respectively. Set D is defined as a set that includes indices of the available data in the azimuth periodically gapped raw data. The quantity of elements in set D is represented as ND. In comparison with the complete SAR raw data, the set of available azimuth sampling time in the azimuth periodically gapped data is denoted as QD.
The slant range model can be regarded as a parabolic approximation of the Taylor expansion, as below:
In Equation (2),
v represents the velocity of the SAR platform, and
R0 represents the closest slant range. By operating Fourier transform (FT) along the range direction, the signal can be approximated as below:
Inspired by PFA [
32], the phase compensation function is designed as below:
The reference slant range at the azimuth time is presented in the following formula:
In Equation (5),
R0,ref is the closest reference slant range. Afterwards, the signal after multiplication with the phase compensation function can be expressed as below:
By implementing inverse FT to
Sc(
τ,
fη) along the range direction, the result can be presented as below:
In Equation (7),
pr denotes the sinc function in the range direction. Substituting Equations (2) and (5) into Equation (7),
sc(
τ,η) can be presented as follows:
As illustrated in Equation (8), the second exponential term shows that the bandwidth of the azimuth modulation is almost removed after phase compensation in the range frequency. In addition, the signal has been compressed in the range direction, as the range modulation has been removed by phase compensation in the range frequency. Consequently, sc(τ,η) is considered to be coarsely compressed in the range of the Doppler domain. In other words, the Sc(τ,fη) is coarsely compressed.
The coarse compression in the range of the Doppler domain after phase compensation is presented in
Figure 3 and
Figure 4.
Figure 3 and
Figure 4 demonstrate the coarse compression of point targets and real SAR data, respectively. In the depiction of the coarse compression of point targets, nine point targets are positioned to generate echo data. A distribution of the nine point targets is displayed in
Figure 3a. The original echo data in the time domain are shown in
Figure 3b. As shown in
Figure 3b, the original echo data are dense in the time domain.
Figure 3c,d illustrates the original echo data and the data with compensation in the range of the Doppler domain, respectively.
Figure 3c shows that the original echo data are also dense in the range of the Doppler domain.
Figure 3d indicates that the data become sparser around the Doppler domain after phase compensation in the range of the frequency domain.
Figure 4a shows the original echo data for real SAR data in the time domain, and
Figure 4b demonstrates the original echo data for real SAR data in the range of the Doppler domain. Moreover, the real SAR data in the range of the Doppler domain after phase compensation is presented in
Figure 4c.
Figure 4c illustrates the real SAR data in coarse compression in the range of the Doppler domain after phase compensation. The
s(
τ,η) denotes the original echo data in the time domain. The
s(
τ,fη) denotes the original echo data in the range of the Doppler domain. The
Sc(
τ,fη) denotes the data in the range of the Doppler domain after phase compensation.
To further verify the coarse compression in the range of the Doppler domain after phase compensation, the analysis of coarse compression is listed in
Table 1. Image contrast (IC) [
35] and Image Entropy (IE) [
36] are chosen as the criteria to assess the sparsity of the original echo data in the time domain, the original echo data in the range of the Doppler domain, and the data in the range of the Doppler domain after phase compensation. The IE and IC in
Table 1 are all obtained with whole images in
Figure 3b–d,
Figure 4a–c. The more concentrated the energy of the SAR image is, the sparser the SAR image is. Moreover, if the energy of the SAR image is more concentrated, the IC of the SAR image has an increasing trend, and the IE of SAR image has a decreasing trend. As demonstrated in
Table 1, the data in the range of the Doppler Domain after phase compensation have the largest IC and smallest IE for point targets and real SAR data, in contrast with the original echo data in the time domain and the range of the Doppler domain. As demonstrated in
Table 1, the effect of concentrating the energy of data is more apparent in point scatters than in real SAR data. Similarly, the presented transformation for making data sparser also has a limited effect on surface scatters. Consequently, it can be concluded that the data in the range of the Doppler Domain after phase compensation are sparser than the original echo data in the time domain and the Doppler domain. In summary, the SAR data become much sparser around the Doppler domain after phase compensation in the range frequency domain.
Although the proposed phase compensation function is effective in the described scenario in
Section 2.1, it also has limitations. The compensation occurs only for the reconstruction strategies because the interpolation error is data dependent. The proposed method performs satisfactorily over point scatters while the performance of the proposed method over surface scatters may decrease. If the platform of SAR has complicated motion rather than uniform linear motion, the approximation in Equation (5) may become invalid. A possible solution for the inaccuracy of Equation (5) is to develop a more accurate range model to accommodate for complicated motion. In addition, the proposed transformation does not consider high squint. Consequently, the proposed phase compensation requires extension in the scenario with high squint. Moreover, the proposed transformation may perform better in a wide-swath scenario with the implementation of a proper sub-block partition.
2.2. Restoration via Deconvolution
As presented in
Section 2.1, the raw data become sparser in the range of the Doppler domain after phase compensation in the range of the frequency domain. Hence, it is feasible to recover the azimuth periodically gapped raw data in the Doppler domain after phase compensation. In this part, the description of restoring the azimuth periodically gapped raw data in the Doppler domain via complex deconvolution is presented.
Figure 5 describes the sampling of SAR azimuth periodically gapped data. The shadow square represents the received pulse and the white square represents the gapped pulse. The complete dataset has N
a sampling pulses, while the gapped data have N
D sampling pulses in the azimuth direction. The azimuth periodically gapped data has N
C clusters of samples, and each cluster contains M
R available pulses and M
G gapped pulses. M
P denotes the periodicity of the gapping and equals the sum of M
R and M
G. Therefore, N
a=(M
R+M
G)N
C=M
PN
C and N
D=M
RN
C. In this paper, the proposed method is developed to cope with the SAR data, which is periodically gapped in the azimuth direction. As a result, the structure of the periodically gapped data is exploited to derive restoration with complex deconvolution in the following section.
Figure 6 demonstrates filling gaps with zeros. As shown in
Figure 6, the positions of gaps are filled with zero vectors. A zero vector has the same size as the pulse in the echo data. Therefore, the size of the data is N
r×N
a after the adding zeros operation.
After zero padding in the gapped positions of the azimuth gapped data, the azimuth periodically gapped raw data can be treated as the multiplication between the complete raw data and the rectangular pulse sequence. The rectangular pulse sequence can be expressed as follows:
In Equation (9), the mod (m,MP) denotes modulo operation, where m is the dividend and MP is the divisor. The modulo operation returns the remainder after the division of m by MP.
Figure 7 presents the demonstration of the rectangular pulse sequence. The rectangular pulse sequence is acquired according to Equation (9). In
Figure 7, O denotes the origin of coordinates. The
y(
m) is plotted on the vertical axis against
m on the horizontal axis in
Figure 7. The black solid lines in
Figure 7 represent elements that equal “1” in the rectangular pulse sequence, and the red solid lines in
Figure 7 represents elements that equal “0” in the rectangular pulse sequence. The
y(
m) is an N
a×1 vector.
Azimuth periodically gapped raw data can be regarded as the multiplication between the complete raw data and rectangular pulse sequence in the azimuth time domain after zero padding. Hence, the azimuth spectrum of gapped data after zero padding can be represented as the convolution between the azimuth spectrum of complete data and the spectrum of the rectangular pulse sequence. Consequently, it is feasible to restore the azimuth spectrum of complete data by deconvoluting the azimuth spectrum of the azimuth periodically gapped data with the spectrum of the rectangular pulse sequence. In complex deconvolution, the spectrum of the rectangular pulse sequence acts as the point spread function. Therefore, it is necessary to derive the expression for the spectrum of the rectangular pulse sequence.
The expression for the spectrum of the rectangular pulse sequence in the discrete domain is derived with Equation (9) and the definition of Fast Fourier Transform (FFT), as follows:
The definitions of
WNa and
q are expressed in Equations (11) and (12), as follows:
As shown in Equation (10), the spectrum of the rectangular pulse sequence can be represented as the multiplication of two geometric sequences. According to the summation formula of the geometric sequence, the spectrum of the rectangular pulse sequence in the discrete domain can be expressed as follows:
Figure 8 presents the procedure for restoration via complex deconvolution. The azimuth periodically gapped raw data are processed in the Doppler domain after phase compensation. The
g(
τ,η) denotes the azimuth periodically gapped data after phase compensation in the range frequency domain and a subsequent adding zeros operation in the time domain. The adding zeros operation fills the positions of gaps with zero vectors. The size of the
g(
τ,η) is N
r×N
a. The
sc(
τ,η) denotes the complete echo data in the time domain after phase compensation in the range frequency domain. The size of
sc(
τ,η) is N
r×N
a.
The N
a×1 vector
x is defined as the transposed vector of any range time
τ in the data
sc(
τ,η). The N
a×1 vector
z is defined as the transposed vector of any range time
τ in the data
g(
τ,η). Thus, there exists a connection, as follows:
In Equation (14), the ◦ denotes the pointwise multiplication operation between two vectors. On the basis of the properties of Fourier transform, the relationship between the spectrums of
x,
y, and
z can be expressed as follows:
In Equation (15), ⊙ denotes the circular convolution operation between two vectors. As the lengths of X, Y, and Z are all Na, the convolution in Equation (15) is circular convolution rather than linear convolution.
This is the key point to solving the unknown X with the known Y and Z in Equation (15). To solve this deconvolution problem more conveniently, it is feasible to transform Equation (15) into another discrete linear system, as follows:
In Equation (16), the matrix
Ψ is the circular convolution operator. Multiplication between the matrix
Ψ and the vector
X equals the circular convolution between vector
Y and vector
X. The matrix
Ψ is a circulant matrix, which is formed with vector
Y according to the definition of circular convolution. The matrix
Ψ can be expressed as follows:
As shown in Equation (17), the matrix Ψ has a form where each row is a cyclic shift of the row above it. The size of the matrix Ψ is Na×Na.
Consequently, the deconvolution problem is transformed by estimating the unknown
X from the known
Z and
Ψ. This problem can be cast as a linear inverse problem, and the ISTA is capable of dealing with this problem. The ISTA (Iterative Shrinkage-Thresholding Algorithm) [
33] solves the linear inverse problem via the method of
l1 regularization. The deconvolution belongs to an ill-conditioned problem and has a very large norm. In this case, regularization is utilized to replace the large norm by approximants with a smaller norm, so numerically stable solutions can be defined and used as meaningful approximations of the true solution corresponding to the exact data [
33]. The
l1 regularization seeks to find the solution of
In Equation (18), the ║•║
1 stands for the sum of the absolute values of the components of
X. The general step of ISTA is
In Equation (19),
t is the proper stepsize,
p denotes the iteration number, and
Γα is the shrinkage operator defined as
In Equation (20), the max(∙) denotes finding the maximum value operation and the sgn(∙) denotes the sign function. As the sign function is included in Equation (20), the shrinkage operator in Equation (20) can only be implemented in the field of real numbers. However, SAR data are complex data. To process complex data, the shrinkage operator needs modification. The modified shrinkage operator for dealing with complex data is given in [
37], as follows:
With the implementation of ISTA via Equations (19) and (21),
X can be restored from the known
Y and
Z via complex deconvolution. Consequently, the azimuth spectrum of complete data can be recovered by deconvoluting the azimuth spectrum of the azimuth periodically gapped data with the spectrum of the rectangular pulse sequence in the range of the Doppler domain. The estimation of
Sc(
τ,fη) is denoted as
, which is restored from
g(
τ,fη) and
Y via the operation of deconvolution. Then, the recovery of the two-dimensional (2D) spectrum of the raw data can be acquired as follows:
The IFTa[∙] denotes inverse Fourier Transform (FT) along azimuth direction. FTa[∙] denotes the FT along the azimuth direction. FTr[∙] denotes the FT along the range direction and conj[∙] represents the conjugate operation. After the raw data have been recovered, traditional SAR imaging algorithms are capable of focusing the recovered SAR raw data.
2.3. Range Migration Algorithm
A brief introduction on the Range Migration Algorithm (RMA) is presented in this section. The RMA is proposed with the condition of uniform linear motion. By operating two-dimensional (2D) FT on Equation (1) along with the range model in Equation (2), the expression of the 2D spectrum of the echo signal can be given as follows:
In Equation (23), fτ and fη are the range frequency and azimuth frequency. In addition, Wr(•) is the envelope of the range frequency and Wa(•) is the envelope of the azimuth frequency.
The first key step in RMA is the Reference Function Multiplication (RFM). The reference function in the 2D frequency domain can be selected as conj[S2df(fτ,fη;Tref)], which is the conjugated 2D spectrum of the reference target. Tref represents the reference point target, and conj[•] represents the conjugation operation.
The step of the RFM operation can be given as follows:
The RFM operation totally removes the range migration of every target in the reference range. However, the RFM only partly removes the range migration of each target in other ranges. Hence, a subsequent Stolt interpolation is used to cancel the residual quadratic and higher order phase modulation. In uniform linear motion, the Stolt interpolation is presented as follows:
By performing the Stolt interpolation, the SAR data are transformed into a new 2D frequency domain (
fτ́,
fη), as follows:
By operating the 2D Inverse FT according to Equation (26), the echo data can be transformed into the time domain. Consequently, a well-focused SAR image is obtained as follows: