1. Introduction
Hyperspectral images (HSIs) usually consist of hundreds of narrow contiguous wavelength bands carrying rich spectral information. With such abundant spectral information, HSIs have been widely used in many fields, such as resource management [
1], scene interpretation [
2], and precision agriculture [
3]. In these applications, a commonly encountered problem is HSI classification, aiming to classify each pixel to one certain land-cover category based on its unique spectral characteristic [
4].
In the last few decades, extensive efforts have been made to fully exploit the spectral information of HSIs for classification, and many spectral classifiers have been proposed, including support vector machines (SVMs) [
5,
6], random forest [
7], and multinomial logistic regression [
8]. However, the classification maps obtained are still noisy, as these methods only exploit spectral characteristics and ignore the spatial contextual information contained in HSIs. To achieve more accurate classification results, spectral-spatial classifiers were developed, which exploit both the spatial and spectral information embedded in HSIs [
9,
10,
11,
12]. In [
11], extended morphological profiles (EMPs) were employed to extract spatial morphological features, which were combined with the original spectral features for HSI classification. In [
12], Kang et al. proposed an edge preserving filtering method for optimizing the pixelwise probability maps obtained by the SVM. In addition, methods of multiple kernel learning [
13,
14], sparse representation [
15,
16], and superpixels [
17] have also been introduced for spectral–spatial classification of HSIs. Nonetheless, the above mentioned methods rely on human engineered features, which need prior knowledge and expert experience during the feature extraction phase. Therefore, they cannot consistently achieve satisfactory classification performance, especially in the face of challenging scenarios [
18].
Recently, deep learning based approaches have drawn broad attention for the classification of HSIs, due to their capability of automatically learning abstract and discriminative features from raw data [
19,
20,
21,
22,
23]. Chen et al. first employed the stacked auto-encoder (SAE) to learn useful high level features for hyperspectral data classification [
24]. In [
25], a deep belief network (DBN) was applied to the HSI classification task. However, owing to the requirement of 1D input data in the two models, the spatial information of HSIs cannot be fully utilized. To solve this problem, a series of convolutional neural network (CNN) based HSI classification methods was proposed, which can exploit the relevant spatial information by taking image patches as input. In [
26], Zhang et al. proposed a dual channel CNN model that combines 1D CNN with 2D CNN to extract spectral-spatial features for HSI classification. In [
27], Zhao et al. employed the CNN and the balanced local discriminative embedding algorithm to extract spatial and spectral features from HSIs separately. In [
28], Devaram et al. proposed a dilated convolution based CNN model for HSI classification and applied an oversampling strategy to deal with the class imbalance problem. In [
29], a 2D spectrum based CNN framework was introduced for pixelwise HSI classification, which converts the spectral vector into 2D spectrum image to exploit the spectral and spatial information. In [
30], Guo et al. proposed an artificial neural network (ANN) based spectral-spatial HSI classification framework, which combines the softmax loss and the center loss for network training. To exploit multiscale spatial information for the classification, image patches with different sizes were considered simultaneously in their model. In addition, 3D CNN models have also been proposed for classifying HSIs, which take original HSI cubes as input and utilize 3D convolution kernels to extract spectral and spatial features simultaneously, achieving good classification performance [
31,
32,
33].
In a CNN model, shallower convolutional layers are sensitive to local texture (low level) features, whereas deeper convolutional layers tend to capture global coarse and semantic (high level) features [
34]. In the above mentioned CNN models, only the last layer output, i.e., global coarse features, is utilized for HSI classification. However, in addition to global features, local texture features are also important for the pixel level HSI classification task, especially when distinguishing objects occupying much smaller areas [
22,
35]. To obtain features with finer local representation, methods that aggregate features from different layers in the CNN were proposed for HSI classification [
36,
37,
38]. In [
36], a multiscale CNN (MSCNN) model was developed, which combines features created by each pooling layer to classify HSIs. In [
37], a deep feature fusion network (DFFN) was proposed, which fuses different levels of features produced at three stages in the network for HSI classification. Although feature fusing mechanisms were utilized in the MSCNN and the DFFN, only three layers were fused for HSI classification. In [
38], Zhao et al. proposed a fully convolutional layer fusion network (FCLFN), which concatenates features extracted by all convolutional layers to classify HSIs. Nonetheless, FCLFN employs a plain CNN model for feature extraction, which suffers from the vanishing gradient and declining accuracy problems when learning deeper discriminative features [
39]. In [
40], a densely connected CNN (DenseNet) was introduced for HSI classification, which divides the network into dense blocks and creates shortcut connections between layers within each block. This connectivity pattern alleviates the vanishing gradient problem and allows the utilization of various features from different layers for HSI classification. However, only layers within each block are densely connected in the network, which presents local dense connectivity pattern and focuses more on the high level features generated by the last block for HSI classification. These methods have demonstrated that taking advantage of features from different layers in the CNN can achieve good HSI classification performance, but not all of them fully exploit the hierarchical features.
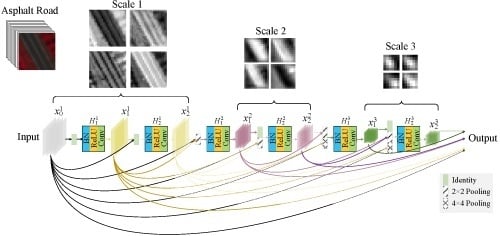
In this paper, inspired by [
41], we propose a novel fully dense multiscale fusion network (FDMFN) to achieve full use of the features generated by each convolutional layer for HSI classification. Different from the DenseNet that only introduces dense connections within each block, the proposed method connects any two layers throughout the whole network in a feed-forward fashion, leading to fully dense connectivity. In this way, features from preceding layers are combined as the input of the current layer, and its own output is fed into the subsequent layers, achieving the maximum information flow and feature reuse between layers. In addition, all hierarchical features containing multiscale information are fused to extract more discriminative features for HSI classification. Experimental results conducted on three publicly available hyperspectral scenes demonstrate that the proposed FDMFN can outperform several state-of-the-art approaches, especially under the condition of limited training samples.
In the rest of this paper,
Section 2 briefly reviews the CNN based HSI classification procedure. In
Section 3, the proposed FDMFN method is described. In
Section 4, the experimental results conducted on three real HSIs are reported. In
Section 5, we give a discussion on the proposed method and experimental results. Finally, some concluding remarks and possible future works are presented in
Section 6.
2. HSI Classification Based on CNN
Deep neural networks can automatically learn hierarchical feature representations from raw HSI data [
42,
43,
44]. Compared with other deep networks, such as SAE [
24], DBN [
25], and the long short-term memory network (LSTM) [
45], CNN can directly take 2D data as input, which provides a natural way to exploit the spatial information of HSIs. Different from natural image classification that uses a whole image input for CNNs, HSI classification, as a pixel level task, generally takes image patches as the input, utilizing the spectral-spatial information contained in each patch to determine the category of its center pixel.
Convolutional (Conv) layers are the fundamental structural elements of CNN models, which use convolution kernels to convolve the input image patches or feature maps to generate various feature maps. Supposing the
lth Conv layer takes
as input, its output
can be expressed as:
where * represents the convolution operator.
and
are the weights and biases of the convolution kernels in the
lth Conv layer, respectively.
Behind each Conv layer, a batch normalization (BN) [
46] layer is generally attached to accelerate the convergence speed of the CNN model. The procedure of BN can be formulated as:
where the learnable parameter vectors
and
are used to scale and shift the normalized feature maps.
To enhance the nonlinearity of the network, the rectified linear unit (ReLU) function [
20] is placed behind the BN layer as the activation layer, which is defined as:
In addition, a pooling layer (e.g., average pooling or max pooling) is periodically inserted after several Conv layers to reduce the spatial size of feature maps, which not only reduces the computational cost, but also makes the learned features more invariant with respect to small transformations and distortions of the input data [
47].
Finally, the size reduced feature maps are transformed into a feature vector through several fully connected (FC) layers. By feeding the vector into a softmax function, the conditional probability of each class can be obtained, and the predicted class is determined based on the maximum probability.
5. Discussion
There are mainly two reasons why FDMFN achieved a superior classification performance. First, the proposed method achieved comprehensive reuse of abundant information from different layers and provided additional supervision for each intermediate layer, enforcing discriminant feature learning. Second, the multiscale hierarchical features learned by all Conv layers were combined for HSI classification, which allowed finer recognition of various objects and hence enhancing the classification performance.
From the comparison of the execution time of different deep neural networks, we can find that the proposed model was not computationally efficient. However, our method could achieve better classification performance in comparison with other methods on the three real hyperspectral datasets. Furthermore, when limited training samples were utilized, the proposed method significantly outperformed other approaches on the IP and KSC datasets, further demonstrating its effectiveness for HSI classification. In our future work, to reduce the computational load, a memory efficient implementation of the proposed network will be investigated.