Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery
Abstract
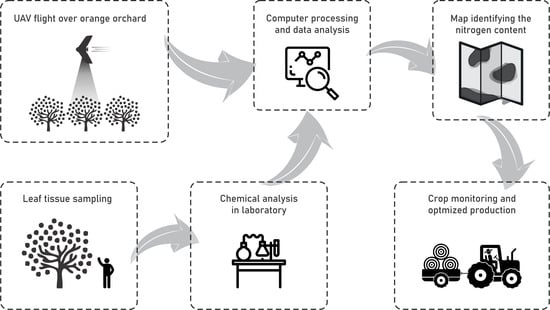
:1. Introduction
2. Related Work
3. Materials and Method
3.1. Data Survey
3.2. Image Pre-Processing and Sampling Points
3.3. Spectral Vegetation Indices
3.4. Analysis
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, S.; Miao, Y.; Yuan, F.; Cao, Q.; Ye, H.; Lenz-Wiedemann, V.I.S.; Bareth, G. In-season diagnosis of rice nitrogen status using proximal fluorescence canopy sensor at different growth stages. Remote Sens. 2019, 11, 1847. [Google Scholar] [CrossRef] [Green Version]
- Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. A new integrated vegetation index for the estimation of winter wheat leaf chlorophyll content. Remote Sens. 2019, 11, 974. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Ge, X.; Shen, P.; Li, W.; Liu, X.; Cao, Q.; Tian, Y. Predicting rice grain yield based on dynamic changes in vegetation indexes during early to mid-growth stages. Remote Sens. 2019, 11, 387. [Google Scholar] [CrossRef] [Green Version]
- Brinkhoff, J.; Dunn, B.W.; Robson, A.J.; Dunn, T.S.; Dehaan, R.L. Modeling mid-season rice nitrogen uptake using multispectral satellite data. Remote Sens. 2019, 11, 1837. [Google Scholar] [CrossRef] [Green Version]
- Tilly, N.; Bareth, G. Estimating nitrogen from structural crop traits at field scale—A novel approach versus spectral vegetation indices. Remote Sens. 2019, 11, 2066. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Jin, X.; Yang, G.; Drummond, J.; Yang, H.; Clark, B.; Zhao, C. Remote sensing of leaf and canopy nitrogen status in winter wheat (Triticum aestivum L.) based on N-PROSAIL model. Remote Sens. 2018, 10, 1463. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, J. Soybean canopy nitrogen monitoring and prediction using ground based multispectral remote sensors. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6389–6392. [Google Scholar] [CrossRef]
- Cilia, C.; Panigada, C.; Rossini, M.; Meroni, M.; Busetto, L.; Amaducci, S.; Boschetti, M.; Picchi, V.; Colombo, R. Nitrogen status assessment for variable rate fertilization in maize through hyperspectral imagery. Remote Sens. 2014, 6, 6549–6565. [Google Scholar] [CrossRef] [Green Version]
- Ciampitti, I.A.; Salvagiotti, F. New insights into soybean biological nitrogen fixation. Agron. J. 2018, 110, 1185–1196. [Google Scholar] [CrossRef] [Green Version]
- Chhabra, A.; Manjunath, K.R.; Panigraphy, S. Non-point source pollution in Indian agriculture: Estimation of nitrogen losses from rice crop using remote sensing and GIS. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 190–200. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Li, D.; Zhou, X.; Yao, X.; Tian, Y.; Zhu, Y. Evaluation of RGB, color-infrared and multispectral images acquired from unmanned aerial systems for the estimation of nitrogen accumulation in rice. Remote Sens. 2018, 10, 824. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Li, W.; Jiang, J.; Liu, Y.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Zhang, Y.; Yao, X. A Comparative assessment of different modeling algorithms for estimating LNC in winter wheat using multispectral images from an unmanned aerial vehicle. Remote Sens. 2018, 10, 2026. [Google Scholar] [CrossRef] [Green Version]
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V.; Halin, A.A.; Ueda, N.; Mansor, S. Land cover classification from fused DSM and UAV images using convolutional neural networks. Remote Sens. 2019, 11, 1461. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Zhu, X.; Lawes, R.; Dunkerley, D.; Zhang, H. Comparison of machine learning algorithms for classification of LiDAR points for characterization of canola canopy structure. Int. J. Remote Sens. 2019, 40, 5973–5991. [Google Scholar] [CrossRef]
- Dyson, J.; Mancini, A.; Frontoni, E.; Zingaretti, P. Deep learning for soil and crop segmentation from remotely sensed data. Remote Sens. 2019, 11, 1859. [Google Scholar] [CrossRef] [Green Version]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Wolanin, A.; Camps-Valls, G.; Gómez-Chova, L.; Mateo-García, G.; van der Tol, C.; Zhang, Y.; Guanter, L. Estimating crop primary productivity with Sentinel-2 and Landsat 8 using machine learning methods trained with radiative transfer simulations. Remote Sens. Environ. 2019, 225, 441–457. [Google Scholar] [CrossRef]
- Ashapure, A.; Oh, S.; Marconi, T.G.; Chang, A.; Jung, J.; Landivar, J.; Enciso, J. Unmanned aerial system based tomato yield estimation using machine learning. Proc. SPIE 11008, Autonomous Air and Ground Sensing Systems for Agricultural Optimization and Phenotyping IV. In Proceedings of the SPIE Defense + Commercial Sensing, Baltimore, MD, USA, 16–18 April 2019. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote sensing approaches for monitoring mangrove species, structure, and biomass: Opportunities and challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Di, L.; Huang, T.; Wang, J.; Lin, L.; Wang, L.; Yang, M. Estimation of leaf nitrogen content in wheat using new hyperspectral indices and a random forest regression algorithm. Remote Sens. 2018, 10, 1940. [Google Scholar] [CrossRef] [Green Version]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Bajpai, V.; Patra, H.; Kumar, S.; Sahoo, P.M. Comparison of various modelling approaches for water deficit stress monitoring in rice crop through hyperspectral remote sensing. Agric. Water Manag. 2019, 213, 231–244. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A random forest machine learning approach for the retrieval of leaf chlorophyll content in wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef] [Green Version]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Miao, Y.; Yuan, F.; Gnyp, M.L.; Yao, Y.; Cao, Q.; Wang, H.; Lenz-Wiedemann, V.I.S.; Bareth, G. Potential of RapidEye and WorldView-2 satellite data for improving rice nitrogen status monitoring at different growth stages. Remote Sens. 2017, 9, 227. [Google Scholar] [CrossRef] [Green Version]
- Kalacska, M.; Lalonde, M.; Moore, T.R. Estimation of foliar chlorophyll and nitrogen content in an ombrotrophic bog from hyperspectral data: Scaling from leaf to image. Remote Sens. Environ. 2015, 169, 270–279. [Google Scholar] [CrossRef]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Baoguo, L. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Cammarano, D.; Fitzgerald, G.J.; Casa, R.; Basso, B. Assessing the robustness of vegetation indices to estimate wheat N in Mediterranean environments. Remote Sens. 2014, 6, 2827–2844. [Google Scholar] [CrossRef] [Green Version]
- Hunt, E.R.J.; Doraiswamy, P.C.; Mcmurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Kooistra, L.; Clevers, J.G.P.W. Estimating potato leaf chlorophyll content using ratio vegetation indices. Remote Sens. Lett. 2016, 7, 611–620. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Y.; Cui, L.; Zhou, X.; Gao, Y.; Fei, T.; Gao, W. Estimation of nitrogen, phosphorus, and potassium contents in the leaves of different plants using laboratory-based visible and near-infrared reflectance spectroscopy: Comparison of partial least-square regression and support vector machine regression methods. Int. J. Remote Sens. 2013, 34, 2502–2518. [Google Scholar] [CrossRef]
- Min, M.; Lee, W. Determination of significant wavelengths and prediction of nitrogen content for citrus. Am. Soc. Agric. Eng. 2005, 48, 455–461. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, J.; Guo, D.; Chang, L.; Huang, D. Non-Invasive Sensing of Nitrogen in Plant Using Digital Images and Machine Learning for Brassica Campestris ssp. Chinensis L. Sensors 2019, 19, 2448. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2013, 34, 712–728. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; van de Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Liu, X.F.; Lyu, Q.; He, S.L.; Yi, S.L.; Hu, D.Y.; Wang, Z.T.; Deng, L. Estimation of carbon and nitrogen contents in citrus canopy by low-altitude remote sensing. Int. J. Agric. Biol. Eng. 2016, 9, 149–157. [Google Scholar] [CrossRef]
- Osco, L.P.; Marques Ramos, A.P.; Saito Moriya, É.A.; de Souza, M.; Marcato Junior, J.; Matsubara, E.T.; Creste, J.E. Improvement of leaf nitrogen content inference in Valencia-orange trees applying spectral analysis algorithms in UAV mounted-sensor images. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101907. [Google Scholar] [CrossRef]
- Katabuchi, M. LeafArea: An R package for rapid digital image analysis of leaf area. Ecol. Res. 2015, 30, 1073–1077. [Google Scholar] [CrossRef]
- Nitrogen Determination by Kjeldahl Method PanReac AppliChem ITW Reagents. Available online: https://www.itwreagents.com/uploads/20180114/A173_EN.pdf (accessed on 9 February 2019).
- Sequoia, P. Parrot Sequoia Manual. © 2019 Parrot Drones SAS. Available online: https://parrotcontact.parrot.com/website/user-guides/sequoia/sequoia_user_guide.pdf (accessed on 19 November 2019).
- Ling, B.; Goodin, D.G.; Mohler, R.L.; Laws, A.N.; Joern, A. Estimating canopy nitrogen content in a heterogeneous grassland with varying fire and grazing treatments: Konza Prairie, Kansas, USA. Remote Sens. 2014, 6, 4430–4453. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Lantinga, E.A.; Schapendonk, A.H.C.M.; Zhong, X. Some quantitative relationships between leaf area index and canopy nitrogen content and distribution. Ann. Bot. 2003, 91, 893–903. [Google Scholar] [CrossRef] [Green Version]
- IDB. Index DataBase. A Database for Remote Sensing Indices. The IDB Project, 2011–2019. Available online: https://www.indexdatabase.de/ (accessed on 7 February 2019).
- XGBoost. eXtreme Gradient Boosting. Available online: https://github.com/dmlc/xgboost (accessed on 23 November 2019).
- Mitchell, T.M. Machine Learning, 1st ed.; McGraw-Hill, Inc.: New York, NY, USA, 1997. [Google Scholar]
- RapidMiner. RapidMiner Python Package. Available online: https://github.com/rapidminer/python-rapidminer (accessed on 23 November 2019).








| Band | Wavelength (nm) | Spectral Resolution | 10 Bits | Flight High | 120 m |
|---|---|---|---|---|---|
| Green | 550 (± 40) | Spatial Resolution | 12.9 cm | Flight Time | 01:30 P.M. |
| Red | 660 (± 40) | HFOV | 70.6° | Weather | Partially cloudy |
| Red-edge | 735 (± 10) | VFOV | 52.6° | Precipitation | 0 mm |
| Near-infrared | 790 (± 40) | DFOC | 89.6° | Wind | At 1–2 m/s |
| Index | Equation | Variable | Scale |
|---|---|---|---|
| ARVI2 (Atmospherically Resistant Vegetation Index 2) | Vitality | Canopy | |
| CCCI (Canopy Chlorophyll Content Index) | Chlorophyll | Leaf/Canopy | |
| CG (Chlorophyll Green) | Chlorophyll | Leaf/Canopy | |
| CIgreen (Chlorophyll Index Green) | Chlorophyll/LAI | Leaf/Canopy | |
| CIrededge (Chlorophyll Index RedEdge) | Chlorophyll/LAI | Leaf/Canopy | |
| Ctr2 (Simple Ratio 695/760 Carter2) | Chlorophyll/Stress | Leaf | |
| CTVI (Corrected Transformed Vegetation Index) | Vegetation | Leaf/Canopy | |
| CVI (Chlorophyll Vegetation Index) | Chlorophyll | Canopy | |
| GDVI (Difference NIR/Green Difference Vegetation Index) | Vegetation | Leaf | |
| GI (Simple Ratio 554/677 Greenness Index) | Chlorophyll | Leaf | |
| GNDVI (Normalized Difference NIR/Green NDVI) | Chlorophyll | Leaf | |
| GRNDVI (Green-Red NDVI) | Vegetation | Leaf/Canopy | |
| GSAVI (Green Soil Adjusted Vegetation Index) | Vegetation | Canopy | |
| IPVI (Infrared Percentage Vegetation Index) | Vegetation | Canopy | |
| MCARI1 (Modified Chlorophyll Absorption in Reflectance Index 1) | Chlorophyll | Leaf/Canopy | |
| MSAVI (Modified Soil Adjusted Vegetation Index) | Vegetation | Canopy | |
| MSR (Modified Simple Ratio) | Vegetation | Leaf | |
| MTVI (Modified Triangular Vegetation Index) | Vegetation | Leaf/Canopy | |
| ND682/553 (Normalized Difference 682/553) | Vegetation | Leaf/Canopy | |
| NDVI (Normalized Difference Vegetation Index) | Biomass/Others | Leaf/Canopy | |
| Norm G (Normalized G) | Vegetation | Leaf/Canopy | |
| Norm NIR (Normalized NIR) | Vegetation | Leaf/Canopy | |
| Norm R (Normalized R) | Vegetation | Leaf/Canopy | |
| OSAVI (Optimized Soil Adjusted Vegetation Index)I | Vegetation | Canopy | |
| RDVI (Renormalized Difference Vegetation Index) | Chlorophyll | Leaf/Canopy | |
| SAVI (Soil-Adjusted Vegetation Index)II | Biomass | Canopy | |
| SR672/550 (Simple Ratio 672/550 Datt5) | Chlorophyll | Leaf | |
| SR750/550 (Simple Ratio 750/550 Gitelson and Merzlyak 1) | Chlorophyll | Leaf/Canopy | |
| SR800/550 (Simple Ratio 800/550) | Chlorophyll/Biomass | Leaf | |
| TraVI (Transformed Vegetation Index) | Vegetation | Leaf/Canopy | |
| TriVI (Triangular Vegetation Index) | Chlorophyll | Leaf/Canopy | |
| SR (Simple Ratio) | Vegetation | Leaf | |
| WDRVI (Wide Dynamic Range Vegetation Index) | Biomass/LAI | Leaf/Canopy |
| Index | R2 | RMSE | Equation | r |
|---|---|---|---|---|
| ARVI2 | 0.12 | 2.014 | y = 67.36x − 31.18 | 0.3504 |
| CCCI | 0.57 | 1.145 | y = 86.55x − 0.004121 | 0.6954 |
| CG | 0.57 | 1.123 | y = 3.008x − 5.782 | 0.6796 |
| CIgreen | 0.26 | 1.853 | y = 3.008x − 2.774 | 0.4796 |
| CIrededge | 0.57 | 1.223 | y = 26.13x + 6.714 | 0.6072 |
| Ctr2 | 0.11 | 2.031 | y = −125.5x + 34.09 | −0.2282 |
| CTVI | 0.12 | 2.020 | y = 178.9x − 184.1 | 0.2430 |
| CVI | 0.51 | 1.359 | y = 3.572x + 0.2191 | 0.6424 |
| GDVI | 0.43 | 1.515 | y = −698.6x2 + 607.1x − 104.9 | 0.5996 |
| GI | 0.30 | 1.797 | y = −23.09x + 62.69 | −0.3493 |
| GNDVI | 0.42 | 1.431 | y = 186x − 126.6 | 0.5853 |
| GRNDVI | 0.26 | 1.821 | y = 82.78x − 33.62 | 0.3996 |
| GSAVI | 0.52 | 1.279 | y = −1608x2 + 1989x − 588.1 | 0.6690 |
| IPVI | 0.13 | 2.006 | y = 87.83x − 51.58 | 0.2607 |
| MCARI1 | 0.45 | 1.188 | y = −394.2x2 + 523.7x − 46.9 | 0.5731 |
| MSAVI | 0.62 | 1.013 | y = −1748x2 + 2431x − 817.1 | 0.7626 |
| MSR | 0.23 | 1.887 | y = 6.52x + 2.101 | 0.3792 |
| MTVI | 0.45 | 1.288 | y = −394.2x2 + 523.7x − 46.9 | 0.5731 |
| ND682/553 | 0.11 | 2.029 | y = 37x + 33.79 | 0.2319 |
| NDVI | 0.12 | 2.014 | y = 78.81x − 43.3 | 0.2504 |
| Norm G | 0.47 | 1.134 | y = −438.4x + 63.11 | −0.6188 |
| Norm NIR | 0.32 | 1.621 | y = 165.6x − 116.4 | 0.4996 |
| Norm R | 0.11 | 2.030 | y = −168.6x + 35.29 | −0.2288 |
| OSAVI | 0.39 | 1.529 | y = 68.43x − 25.89 | 0.5032 |
| RDVI | 0.54 | 1.154 | y = −2168x2 + 2671x − 795.3 | 0.6028 |
| SAVI | 0.58 | 1.045 | y = −2123x2 + 2747x − 861.5 | 0.6813 |
| SR672/550 | 0.10 | 2.175 | y = −881.4x2 + 1197x − 379.4 | 0.0982 |
| SR750/550 | 0.61 | 1.022 | y = 7.301x − 18.77 | 0.7991 |
| SR800/550 | 0.57 | 1.083 | y = 3.008x − 5.782 | 0.7296 |
| TraVI | 0.12 | 2.020 | y = 178.9x − 184.1 | 0.2430 |
| TriVI | 0.63 | 1.001 | y = −0.782x2 + 24.49x − 164.3 | 0.8012 |
| VIN | 0.27 | 1.832 | y = 0.9866x + 9.754 | 0.3238 |
| WDRVI | 0.58 | 1.076 | y = −466.2x2 + 238.9x − 3.666 | 0.7166 |
| Model | MSE | CVRMSE | MAE | R2 |
|---|---|---|---|---|
| Support Vector Machine | 2.055 | 5.149 | 1.011 | 0.65 |
| Decision Tree | 0.347 | 2.225 | 0.462 | 0.85 |
| Random Forest | 0.307 | 2.098 | 0.341 | 0.90 |
| Random Forest (XGBoost) | 0.300 | 2.043 | 0.327 | 0.90 |
| Artificial Neural Network | 1.676 | 4.168 | 0.865 | 0.70 |
| Linear Regression (Ridge) | 2.041 | 5.895 | 0.984 | 0.63 |
| Linear Regression (Lasso) | 2.010 | 5.790 | 0.965 | 0.65 |
| Model | Indices (n) | MSE | CVRMSE | MAE | R2 |
|---|---|---|---|---|---|
| Random Forest | 5 | 0.376 | 2.342 | 0.477 | 0.83 |
| Random Forest (XGBoost) | 5 | 0.350 | 2.253 | 0.412 | 0.85 |
| Random Forest | 10 | 0.345 | 2.215 | 0.401 | 0.85 |
| Random Forest (XGBoost) | 10 | 0.318 | 2.127 | 0.357 | 0.88 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prado Osco, L.; Marques Ramos, A.P.; Roberto Pereira, D.; Akemi Saito Moriya, É.; Nobuhiro Imai, N.; Takashi Matsubara, E.; Estrabis, N.; de Souza, M.; Marcato Junior, J.; Gonçalves, W.N.; et al. Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery. Remote Sens. 2019, 11, 2925. https://doi.org/10.3390/rs11242925
Prado Osco L, Marques Ramos AP, Roberto Pereira D, Akemi Saito Moriya É, Nobuhiro Imai N, Takashi Matsubara E, Estrabis N, de Souza M, Marcato Junior J, Gonçalves WN, et al. Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery. Remote Sensing. 2019; 11(24):2925. https://doi.org/10.3390/rs11242925
Chicago/Turabian StylePrado Osco, Lucas, Ana Paula Marques Ramos, Danilo Roberto Pereira, Érika Akemi Saito Moriya, Nilton Nobuhiro Imai, Edson Takashi Matsubara, Nayara Estrabis, Maurício de Souza, José Marcato Junior, Wesley Nunes Gonçalves, and et al. 2019. "Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery" Remote Sensing 11, no. 24: 2925. https://doi.org/10.3390/rs11242925
APA StylePrado Osco, L., Marques Ramos, A. P., Roberto Pereira, D., Akemi Saito Moriya, É., Nobuhiro Imai, N., Takashi Matsubara, E., Estrabis, N., de Souza, M., Marcato Junior, J., Gonçalves, W. N., Li, J., Liesenberg, V., & Eduardo Creste, J. (2019). Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery. Remote Sensing, 11(24), 2925. https://doi.org/10.3390/rs11242925