Color Calibration of Proximal Sensing RGB Images of Oilseed Rape Canopy via Deep Learning Combined with K-Means Algorithm

Abstract

Plant color is a key feature for estimating parameters of the plant grown under different conditions using remote sensing images. In this case, the variation in plant color should be only due to the influence of the growing conditions and not due to external confounding factors like a light source. Hence, the impact of the light source in plant color should be alleviated using color calibration algorithms. This study aims to develop an efficient, robust, and cutting-edge approach for automatic color calibration of three-band (red green blue: RGB) images. Specifically, we combined the k-means model and deep learning for accurate color calibration matrix (CCM) estimation. A dataset of 3150 RGB images for oilseed rape was collected by a proximal sensing technique under varying illumination conditions and used to train, validate, and test our proposed framework. Firstly, we manually derived CCMs by mapping RGB color values of each patch of a color chart obtained in an image to standard RGB (sRGB) color values of that chart. Secondly, we grouped the images into clusters according to the CCM assigned to each image using the unsupervised k-means algorithm. Thirdly, the images with the new cluster labels were used to train and validate the deep learning convolutional neural network (CNN) algorithm for an automatic CCM estimation. Finally, the estimated CCM was applied to the input image to obtain an image with a calibrated color. The performance of our model for estimating CCM was evaluated using the Euclidean distance between the standard and the estimated color values of the test dataset. The experimental results showed that our deep learning framework can efficiently extract useful low-level features for discriminating images with inconsistent colors and achieved overall training and validation accuracies of 98.00% and 98.53%, respectively. Further, the final CCM provided an average Euclidean distance of 16.23 ΔΕ and outperformed the previously reported methods. This proposed technique can be used in real-time plant phenotyping at multiscale levels.

1. Introduction

The digital camera has emerged as an essential tool for high-throughput plant phenotyping, and it is widely used to reveal genotypic traits associated with the structure and color of plants. The reliability and repeatability of these traits are highly related to the color constancy of the images [1]. However, images acquired using different digital cameras (or the same camera with changing its settings) produce an inconsistent color, due to the different specifications (e.g., spatial resolution, spectral responses, and signal-to-noise ratio). Moreover, images captured using the same camera at different points in time and dates could vary in color, despite no changes in the object (e.g., plant) characteristics. In such cases, the variability in the image color is a result of sunlight intensity, sun inclination angle, temperature, and other prevailing weather conditions. Such variations in image color have a serious influence on the evaluation of plant physical, chemical, and biological characteristics when color is considered as a relevant and significant trait in studying plant phenotyping [2,3].

Color is an important feature that needs to be automatically characterized by the computer vision-based plant phenotyping measurements [4,5,6]. One of the image processing steps for extracting the plant phenotypic traits is image segmentation, which is considerably dependent on the image color feature [7]. The variability in image color could lead to poor and inconsistent image segmentation results [8]. Barbedo [9] reported that illumination variations during image acquisition under uncontrolled conditions are a critical issue in image segmentation and feature extraction that should be taken care of. Therefore, color-based features extracted from such digital camera images to assess plant phenotypic traits could lead to inaccurate results due to variability in lighting conditions. The color-based features were also used as an early indicator of plant stress due to biotic and abiotic factors, and it was found that they can highly correlate with plant physiological traits like chlorophyll content [10,11]. Furthermore, the color is essential in understanding the degradation of phenolic and antioxidant content of herbal plants during the storage under normal conditions. It was found to be a valuable feature to evaluate the conservation status of plants for preparing infusions, as it can be visually observed [12]. Image color features have also been used as parameters to establish and characterize global biological changes (e.g., ocean and vegetation ecosystems) extracted from satellite-based color images [13,14]. However, visual image color estimation is ephemeral, subjective, and susceptible to changes in plant age, time of the day, weather, adjacent object color, and haze [15]. Without efficient and accurate color calibration, researchers have not been able to estimate and describe plant colors precisely [16].

Generally, the color calibration methods can be divided into two groups: (i) device-based methods and (ii) image-based methods. The former approach has been investigated in several studies, in which the sensor of the camera was established to automatically adjust the color values based on the scene lighting conditions [17,18]. While the latter methods are used to compensate for color distortion due to variations in illumination conditions or different responses of camera sensors. The image-based approach is the most popular way to preserve the same color tone in object scenes and it often uses a standard color chart to transform the pixel values of an image to the target color values measured under know-illuminant [19,20]. Various types of relationships between pixel values of the image and the reference color values have been already established in the literature. For instance, color calibrations using least-squares polynomial regression [21,22,23], linear regression [24], and neural networks [25] were previously established, and they have been applied successfully in different areas such as dentistry [26], photography [27,28], printing technologies [29], and the food industry [24,30]. However, there is insufficient information about color calibration for agricultural applications. Akkaynak et al. [31] introduced a color calibration method using a color calibration chart. This method performed color calibration using a three-dimension (XYZ) color space and then converted the image into the RGB color space for better display. Shajahan et al. [20] developed an efficient semi-automated color calibration method using linear regression. In their method, the optimum number of color patches of a color chart that can provide accurate image calibration was specified. Although the regression-based methods are computationally inexpensive and do not need training datasets, their real-time applications under in situ field conditions are difficult, particularly for plant phenotyping whereby a large number of images are commonly collected on a daily basis. Also, these regression-based methods are time-consuming, laborious, and require the color checker to be included in every image. An automated and efficient approach for image color standardization is therefore highly required.

In this study, we developed an automated approach for image color calibration using a deep learning framework combined with a k-means algorithm. Deep learning networks have proved to be valuable for automatically learning representative features from large datasets. Among many deep learning approaches, convolutional neural networks (CNNs) have recently gained considerable attention due to their outstanding success in studies related to object detection [32,33], classification [34], and recognition [35]. One of the essential reasons for the high capability of deep CNN in resolving various complex computer vision problems is that it does not require hand-engineered features such as scale-invariant feature transform (SIFT) and speeded up robust features (SURF) features [36,37]. Instead, CNN automatically learns useful representative features from a huge number of image datasets during the training process. Inspired by these learning capabilities, deep learning-based methods for the illuminant’s color estimation have recently been proposed [38,39,40]. In these methods, the illuminant’s color estimation is dealt with as a regression problem. CNN is employed to correlate pixel values with the scene-illuminant chromaticity and produce a reasonably accurate result. However, the main difference between our proposed method and the previously developed deep learning-based methods for image color calibration is that we dealt with the image color calibration issue as a classification issue. CNN learned useful low-level features through the training process. The learned features are then used to efficiently distinguish the classes of training samples acquired under different illumination conditions. The outputs (probabilities) of the CNN are then used as dynamic fusion weights to fuse the output of the unsupervised k-means algorithm (final color calibration matrix (CCM) estimate). As far as we know, the deep learning technique has not been applied for calibrating the color of agricultural images. This technique is mainly for application related to high-throughput image-based plant phenotyping where color features are beneficial to estimate plant (e.g., oilseed rape) physiological traits.

The objective of this study was to develop a deep learning-based framework for automatic color calibration of proximal sensing RGB images. Specifically, we combined CNN and unsupervised k-means algorithm to estimate the CCM efficiently. We demonstrated that our framework can produce output images with a consistent color in an automated fashion and outperformed previously reported methods.

2. Materials and Methods

2.1. Image Acquisition and Camera Parameters

A total of 3150 RGB images were collected using a portable visible light camera (model: PowerShot SX720 HS, Canon Inc., Tokyo, Japan) for oilseed rape experimental plots at the Agricultural Research Station of Zhejiang University (30°16′N, 120°07′07″E), Hangzhou City, Zhejiang Province, P.R. China. The camera was installed on a tripod, keeping a distance of 1.1 m from the crop canopy with a field of view of 53.1 o. All acquired images were saved in RAW image quality with a spatial resolution of 3888 × 5186 pixels. The color calibration chart was placed in such a way to be viewed at the image corner. The images were captured on sunny and cloudy days in the morning (08:30–11:30 local time) and afternoon (13:30–17:30 local time) Greenwich Mean Time (GMT+8). The image samples were divided into 67% (2100), 28% (900), and 5% (150) for the training, validation, and testing of our CNN modelling framework for the CCM estimation, respectively.

It is worth mentioning that variations in the image illumination were not only due to outdoor lighting that struck the camera sensor but also due to using different camera parameter settings, such as aperture settings (f-stop) and manual white balance [41]. In our experiment, all camera parameters were set and optimized, except for the aperture and the white balance. The aperture or opening of a camera lens varied from f/3.3 to f/8. The white balance (WB) was set manually to daylight, cloudy, tungsten, fluorescent to simulate capturing images in different lighting conditions. For example, daylight WB for shooting outdoor on clear days, cloudy for shooting on cloudy days or in the shade, tungsten for shooting under tungsten lighting, and fluorescent under white fluorescent light. However, to make a significant variation on the dataset, all these settings were used under sunny and cloudy days.

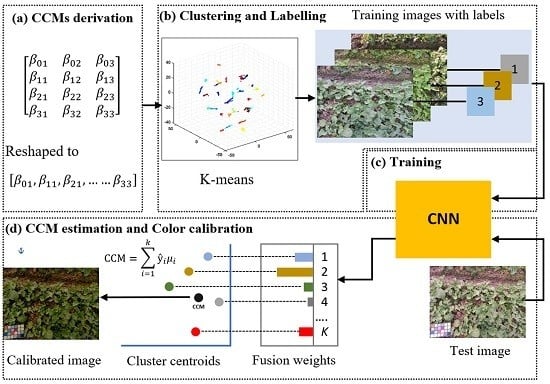
2.2. Overview of the Proposed Method

We proposed to combine the k-means algorithm and deep learning to calibrate the color of our images. Specifically, our proposed framework includes four main steps, as described in Figure 1: (a) the color calibration matrix of each image was firstly computed (ground truth, it should be noted that the manually derived CCM is a ground truth to the final CCM estimated using CNN. The reader should not confuse between this ground truth and standard color values supplied by the X-Rite company.); (b) the training images were categorized based on the color calibration matrix allocated to each image sample; (c) a labeled image dataset was then used to train and validate self-designed deep CNN, and the system was trained to assign scores to a given image to belong to each CCM cluster with some degree of membership; and (d) the CCM of a testing image was calculated by combining the outputs of our deep learning CNN and cluster centroids of the k-means algorithm.

2.2.1. Color Calibration Matrices Derivation

In order to minimize the difference between the standard and measured color values, linear multivariate regression (Equations (1) and (2)) was utilized to regress the average RGB values measured from each color patch (i.e., using the color calibration chart in the acquired image) to the standard color values as suggested by the X-Rite company [42].

$${\mathit{S}}_{\left(\mathit{R}\mathit{G}\mathit{B}\right)\mathit{i}}={\mathit{I}}_{\left(\mathit{R}\mathit{G}\mathit{B}\right)\mathit{i}}\mathit{C}\mathit{C}\mathit{M}$$

(1)

In expanded form

$$\left[\begin{array}{ccc}{\mathit{S}}_{\mathit{R}\mathbf{1}}& {\mathit{S}}_{\mathit{G}\mathbf{1}}& {\mathit{S}}_{\mathit{B}\mathbf{1}}\\ \begin{array}{c}{\mathit{S}}_{\mathit{R}\mathbf{2}}\\ ⋮\end{array}& \begin{array}{c}{\mathit{S}}_{\mathit{G}\mathbf{2}}\\ ⋮\end{array}& \begin{array}{c}{\mathit{S}}_{\mathit{B}\mathbf{2}}\\ ⋮\end{array}\\ {\mathit{S}}_{\mathit{R}\mathit{n}}& {\mathit{S}}_{\mathit{G}\mathit{n}}& {\mathit{S}}_{\mathit{B}\mathit{n}}\end{array}\right]=\left[\begin{array}{cccc}\mathbf{1}& {\mathit{I}}_{\mathit{R}\mathbf{1}}& {\mathit{I}}_{\mathit{G}\mathbf{1}}& {\mathit{I}}_{\mathit{B}\mathbf{1}}\\ \begin{array}{c}\mathbf{1}\\ ⋮\end{array}& \begin{array}{c}{\mathit{I}}_{\mathit{R}\mathbf{2}}\\ ⋮\end{array}& \begin{array}{c}{\mathit{I}}_{\mathit{G}\mathbf{2}}\\ ⋮\end{array}& \begin{array}{c}{\mathit{I}}_{\mathit{B}\mathbf{2}}\\ ⋮\end{array}\\ \mathbf{1}& {\mathit{I}}_{\mathit{R}\mathit{n}}& {\mathit{I}}_{\mathit{G}\mathit{n}}& {\mathit{I}}_{\mathit{B}\mathbf{3}}\end{array}\right]\left[\begin{array}{ccc}{\mathit{\beta }}_{\mathbf{01}}& {\mathit{\beta }}_{\mathbf{02}}& {\mathit{\beta }}_{\mathbf{03}}\\ \begin{array}{c}{\mathit{\beta }}_{\mathbf{11}}\\ {\mathit{\beta }}_{\mathbf{21}}\end{array}& \begin{array}{c}{\mathit{\beta }}_{\mathbf{12}}\\ {\mathit{\beta }}_{\mathbf{22}}\end{array}& \begin{array}{c}{\mathit{\beta }}_{\mathbf{13}}\\ {\mathit{\beta }}_{\mathbf{23}}\end{array}\\ {\mathit{\beta }}_{\mathbf{31}}& {\mathit{\beta }}_{\mathbf{32}}& {\mathit{\beta }}_{\mathbf{33}}\end{array}\right]$$

(2)

where S and I are standard and measured color values and subscripts R, G, and B are the R-channel, G-channel, and B-channel of RGB color space, respectively. n is the number of color patches, and in our case, there were 24 color patches. The CCMs were represented by the coefficients of the linear multiple regression model. Then the CCM was reshaped to a 1 × 12 row vector as follows (Equation (3)):

$$\left[{\mathit{\beta }}_{\mathbf{01}},{\mathit{\beta }}_{\mathbf{11}},{\mathit{\beta }}_{\mathbf{21}},{\mathit{\beta }}_{\mathbf{31}},{\mathit{\beta }}_{\mathbf{02}},{\mathit{\beta }}_{\mathbf{12}},{\mathit{\beta }}_{\mathbf{22}},{\mathit{\beta }}_{\mathbf{32}},{\mathit{\beta }}_{\mathbf{03}},{\mathit{\beta }}_{\mathbf{13}},{\mathit{\beta }}_{\mathbf{23}},{\mathit{\beta }}_{\mathbf{33}}\right]$$

(3)

A total of 3000 CCMs were derived from training and validation image samples (3000 images) and concatenated to form a 3000 × 12 matrix. This matrix was used as the input of the k-means algorithm to provide two outputs, including cluster centers and labels, as described in the next subsection. The CCMs derivation method in this study was modified from work by Shajahan et al. [20]. We derived 4 × 3 CCM that performed both rotation and translation to the color space, which could improve the calibration performance compared with the 3 × 3 CCM that excluded the bias or translation term.

2.2.2. Clustering and Image Labeling

Image clustering is considered as one of the vital steps that improves the performance of the CNN model to estimate the CCMs. In principle, the CNN learns rich features that can best distinguish among different classes [43]. The CNN model is expected to perform more accurately in the cases where classes are well separable as opposed to the cases where the classes are indistinguishable. The CCMs estimation problem falls in the indistinguishable classis’s scenario because images acquired under very similar illumination conditions have similar CCMs. If we directly trained our deep CNN model on this image dataset without grouping, the CNN model might have not been able to distinguish the classes accurately. Therefore, we proposed to first group the images into categories according to the CCM assigned to each image, so as to maximize inter-class differences. This could improve the performance of our CNN model. We employed the k-means algorithm for this purpose. The number of the clusters k was defined using sort of domain knowledge about the illumination variations of our image dataset, which is associated with the number of camera parameters and weather conditions. After the grouping, the labeled images were for training and validation of the deep CNN model.

2.2.3. Network Architecture and Training Strategy

After a large number of experiments in which we adjusted the architecture of the network, the sequence of layers was selected taking into account both classification accuracy and training difficulty (see Figure 2 for a graphical representation). The CNN architecture consists of ten convolutional layers (Conv.), two fully-connected (FC) layers, and four max-pooling layers. Each convolution layer is followed by a batch normalization (BN) layer and a rectified linear unit (ReLU) layer. The first FC layer had a 4096 dimensional activation vector and followed by the ReLU layer. The number of output neurons in the final FC layer was set to 30 to be equivalent to the classes used in our study. The softmax layer was stacked at the end to provide probability distribution for the classes (optimal fusion weights). Other hyperparameters of the CNN included filter size, number of filters, and the stride, which were borrowed from the visual geometry group network [35]. We used 3 × 3 receptive fields throughout the network, which were convolved with input at every pixel. The stack of two consecutive 3 × 3 Conv. layers (without spatial pooling in between) had an effective receptive field of 5 × 5, and three such layers had a 7 × 7 effective receptive field, which allowed us to incorporate three ReLU layers instead of a single one and make the decision function more discriminative. By using the small receptive field, the number of parameters can be decreased significantly, and therefore reducing the computation time. Small-size convolution filters have been previously employed by Ciresan et al. [44], but their network is larger than ours. The four max-pooling layers followed some of the Conv. layers instead of all of them, and they were performed over a 2 × 2 pixel window with the stride of 1 × 1. The width of Conv. layers (the number of channels) started from 64 in the first layer and then increased by a factor of two after each max-pooling layer until it reached 512. The number of Conv. layers was decided by fixing the other parameters of the network and steadily increased the depth of the network by adding more convolutional layers until there was no improvement in the validation accuracy. As the network is utilized to provide optimum fusion weights, we placed the softmax layer at the end of the CNN to output a probability distribution over 30 classes [45,46]. The fusion weights were a column vector whose length is equal to k elements and sum to 1. Our final goal of the proposed framework was to compute the CCM, so we should infer the precise CCM from the outputs of the CNN. The estimation procedure of the CCM is described in the following subsection.

Images were resized to 224 × 224 × 3 to match the input of the CNN. During the training of the CNN, the color checker chart was masked out to control its influence on the CNN, and to come up with a model that can describe a real-world application. The CNN model learnable parameters were optimized with the stochastic gradient descent with a momentum of 0.09, a mini-batch size of 66 samples, a learning rate of 0.001, and max epochs of 20. All our modelling framework procedures were conducted in MATLAB 2018a (MathWorks, Inc., Natick, Massachusetts, United States) using deep learning, statistics, machine learning, and computer vision ToolboxTM as a computing software. Our model was run on a graphics processing unit NVIDIA GeForce GTX1080Ti equipped with 3548 compute unified device architecture (CUDA) Cores and 16 GB of graphics processing unit (GPU) memory.

2.2.4. The Network Testing and Image Color Calibration

As already mentioned, our deep CNN was trained to provide the probability (P) of an input image x belonging to one of the k CCM groups. We estimated the CCM of a certain input image from the prediction: ŷ = N(x) using Equation (4).

$$\mathbf{ŷ}=\left[\begin{array}{c}\mathit{P}\left(\mathit{y}=\mathbf{1}|\mathit{x}\right)\\ \begin{array}{c}\mathit{P}\left(\mathit{y}=\mathbf{2}|\mathit{x}\right)\\ ⋮\end{array}\\ \mathit{P}\left(\mathit{y}=\mathit{k}|\mathit{x}\right)\end{array}\right]$$

(4)

One trivial solution to calculate the CCM is to take the one center of the k-means clusters that corresponds to the highest probability given by the deep CNN model. However, this solution is not suitable for estimating the CCM, because it constrains the possible CCM to only one class. Therefore, we estimated the final CCM by calculating the weighted average of all cluster centers of the k-means (µ) with the fusion weights being P(y = i|x) from the network output following Equation (5), a so-called soft combination method [47,48].

$$\mathbf{C}\mathbf{C}\mathbf{M}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{k}}{\mathbf{ŷ}}_{\mathit{i}}{\mathit{\mu }}_{\mathit{i}}$$

(5)

Using the soft combination method enables our system to estimate the CCM more accurately. As shown in Figure 3, the computed CCM is indicated by a yellow dot, the blue squares show the k-means cluster centers, and the percentage numbers denote the membership scores of a certain image belonging to each CCM class. The CCM was calculated as a weighted average of the cluster centers with the fusion weights being the scores from the deep CNN. The ground truth (GT) is shown as a red diamond. It needs to be mentioned that the 12 length CCM was projected onto a 2D plane in order to obtain a better visualization. This method supposed that the color of the illuminant is spatially unvarying across the image scene. Hence, after the global estimation of the CCM, it can be applied to the uncalibrated image to obtain an image with standard color values. It needs to be mentioned that the standard RGB (sRGB) color space used throughout this work is the linear sRGB color space, in which the gamma-correction was removed.

2.3. Performance Evaluation of the Proposed Framework

The CCM derivation method (4 × 3 CCM) using multivariate linear regression was compared to the method (3 × 3 CCM) proposed by Shajahan et al. [20]. In order to demonstrate the success of the k-means algorithm for accurately differentiating among the image classes based on the CCM assigned to each image, the 12 length CCMs were projected onto a 3D plane using a t-distributed stochastic neighbor embedding (t-SNE) technique [49]. It is a common technique used to reduce non-linear dimensional data. One merit of this technique is that it attempts to preserve the distribution of clusters in the original high-dimensional space when projecting the data into a 3D plane for visualization purposes.

To evaluate the performance of the CNN, a confusion matrix was used to summarize the precision and recall of each class, and the overall accuracy was also computed using Equation (6). We compared the measured color of the uncalibrated image and the standard color on a color reference chart. The color values of the calibrated image were also assessed based on a reference color value. Furthermore, we used Delta_E (ΔΕ) calculated with Equation (7) to measure the color difference among the measured and the reference color values in the international commission on illumination (CIE) 1976 L*a*b* color model. The lower the value of ΔΕ (approach to 1), the more accurate the color calibration is.

$$\mathit{O}\mathit{v}\mathit{e}\mathit{R}\mathit{a}\mathit{l}\mathit{l}\mathit{a}\mathit{c}\mathit{c}\mathit{u}\mathit{R}\mathit{a}\mathit{c}\mathit{y}=\frac{\mathit{T}\mathit{P}+\mathit{T}\mathit{N}}{\mathit{T}\mathit{P}+\mathit{T}\mathit{N}+\mathit{F}\mathit{P}+\mathit{F}\mathit{N}}$$

(6)

$$\Delta \mathit{E}=\frac{\mathbf{1}}{\mathbf{24}}\left[{\displaystyle \sum }_{\mathbf{1}}^{\mathbf{24}}\sqrt{{\left({\mathit{L}}_{\mathbf{2}}^{*}-{\mathit{L}}_{\mathbf{1}}^{*}\right)}^{\mathbf{2}}+{\left({\mathit{a}}_{\mathbf{2}}^{*}-{\mathit{a}}_{\mathbf{1}}^{*}\right)}^{\mathbf{2}}+{\left({\mathit{b}}_{\mathbf{2}}^{*}-{\mathit{b}}_{\mathbf{1}}^{*}\right)}^{\mathbf{2}}}\right]$$

(7)

We also tested the color consistency among images acquired from the same plot under different illumination conditions and used different camera parameter settings. The color intensities of the RGB channels of these images were compared before and after image calibration. Finally, to further confirm the claim considering the progress being made using deep learning methods for image color calibration, the output of our proposed method was compared with previously reported color calibration algorithms, including gray world (GW) [50], principal component analysis (PCA) [51], and white patch (WP) [52]. The comparison was performed using the test dataset (i.e., 150 images). The performance of these algorithms was evaluated by implementing different metrics to describe the error distribution, including mean (µ), median, trimean, best-25% (µ), and worst-25% (µ). In addition to these summarizing statistics, more insight into the performance of the algorithms can be obtained by performing a significant test, like Wilcoxon signed-rank test, which is usually performed between two methods to show that the difference between two algorithms is statistically significant [53].

3. Results and Discussion

In this section, we first demonstrate the improvement being made to the CCM derivation method by comparing it with a method proposed in the literature and then verify the capability of the k-means algorithms for correctly clustering or grouping the images according to the CCM assigned to each image. The classification results of CNN are summarized using a confusion matrix, followed by the evaluation of the CNN training process. The calibration performance of the proposed framework is discussed in two scenarios; in the first scenario, we introduce and discuss the results of the color errors between measured and target colors; while in the second scenario, we demonstrate the color consistency between the calibrated images and discuss its implications for real-world applications. Finally, we prove the claim that using our framework adds considerable enhancement by comparing it with commonly used statistical-based methods in terms of both calibration accuracy and computation time.

3.1. The CCMs Derivation

The CCM derivation is a very critical step in our framework because the CCMs manually derived from whole image samples will finally be combined into one optimal CCM, as described in Section 2.2.4. As depicted in Figure 4, the proposed CCM derivation method reveals that when adding bias or a translation component to the CCM, the color difference between the measured and reference color values was less than 17 ΔΕ, while it was larger than 30 ΔΕ by using 3 × 3 CCM. The color model plays a key role in the color calibration process and can significantly influence the calibration accuracy. This study only used sRGB color space for color calibration, therefore the influence of different color spaces is a topic for future research. Since the digital camera produces non-linearized gamma-corrected images, the linearization of gamma-corrected sRGB color space is an essential step when using sRGB color space with multivariate linear regression. Because the CCM derived by multivariate linear regression only performs a linear transformation, it cannot work well with sRGB color space without removing gamma-correction or linearizing the image. Otherwise, high-order polynomial regression is highly recommended to obtain the mapping coefficient matrix without image linearization [54].

3.2. Performance of the K-Means Clustering

Figure 5 shows the result of the k-means clustering of images based on the CCMs similarity. The classes can be easily discriminated on the 3D space, which reveals that the k-means algorithm can cluster CCMs further apart. We observed that the images acquired under similar illumination conditions often have the same CCM. Therefore, grouping such images together will improve the classification performance of the CNN model. Although many unsupervised learning algorithms (such as the Gaussian mixture model and self-organizing map) can be combined with CNN, the k-means algorithm is simple and more computationally efficient for practical applications [3]. It needs to be mentioned that the optimal number of classes should be carefully selected when combining the k-means algorithm with CNN. When k is small, the training of the deep CNN can be easily performed to classify a test image accurately, but the CCM could not be well estimated from the coarse probability distribution. In contrast, when k is large, the training of CNN becomes difficult, but more accurate CCM can be calculated for correctly classified image samples. Therefore, a trade-off between the complexity of training CNN and final CCM approximation should be considered when selecting k. In our study, the k was selected using some sort of domain knowledge about the variations in the illumination of our image samples, which is associated with the number of camera parameters and variation in the outdoor illumination conditions.

3.3. Performance Evaluation of the CNN Classification

Figure 6 shows the confusion matrix for the CNN classification performance. Our results show that most of the classes were correctly classified with a precision and recall of 100%. Class 17 was partially confused with class 30, which could be due to the similarity between the illumination of two classes.

The CCN model yielded an overall training accuracy of 98.00%, validation accuracy of 98.53 %, and the training time of 2345 minutes, as shown in

Table 1. Overall accuracies of the convolutional neural network (CNN) for training and validation images. Note that classification time denotes the time needed to classify one image and does not include the time needed for color calibration. The training time is the time required to train the entire network from scratch over 20 epochs, and no stopping criterion was used.

Training No. of Images	Validation No. of Images	Training Time (min)	Classification Time (s/Image)	Training Accuracy (%)	Validation Accuracy (%)
2100	900	2345	0.12	98.00	98.53

. This high training accuracy indicated that the model successfully fit the training dataset. No overfitting problem was observed during the entire training process with a very small difference of 0.53% between the training and the validation accuracies. Besides, the training time was also reasonable since the model only needs to be trained one time. Further, our results showed that the classification was fast enough for real-time applications in the field condition with the classification time of 0.12 s.

Figure 7 shows the training and validation accuracies and losses for each iteration of the training and validation image dataset using the CNN classification model. The training and validation accuracies are gradually improved even after 190 iterations and the training and validation losses more or less established after 150 iterations. This result indicates that CNN has reached the highest accuracy and the lowest loss and did not require any more epochs or iterations. No overfitting problem was observed during the whole training process.

3.4. Performance of Image Color Calibration

In the first column of Figure 8, we showed the imaging conditions and camera parameters as an example of the test images. Because of the different illumination conditions and/or settings of the camera parameters, there was a color inconsistency among images. After applying the color calibration, all the images were turned into a similar color characteristic, as shown in the third column of Figure 8. Based on the visual assessment, it appears reasonable to claim that with using deep learning, the color values of the resulting calibrated images were brought to the reference color values measured under known illuminants.

It is worth mentioning that the color change characteristics of the plant canopy are not only due to variation of illumination conditions, but it is also related to illumination-observation geometries. The plant behaves as an anisotropic reflector that requires characterization of the spectral reflectance (and therefore color) in the different irradiation/viewing directions. Therefore, to account for the effects of illumination and observation directions, it would be better to train the CNN model using images collected from different viewing zenith/azimuth angles.

The quantitative analysis results of the differences between the measured and reference colors before and after the color calibration are presented in Figure 9. It was observed that the measured color errors were smaller for the calibrated image (ranging between 4.9 ΔΕ and 30.70 ΔΕ) than those in the original image (ranging between 4.20 ΔΕ and 66.00 ΔΕ), indicating the colors of the color-corrected image better agreed with the reference colors in most color patches, except in the patch 19 whereby the measured color error of 20.2 ΔΕ was relatively high.

Figure 10 shows mean canopy color in RGB channels for 100 images of a single oilseed rape plot acquired under different illumination conditions using different camera parameter settings. The aim of this figure is not to prove the mean color intensities themselves, but rather to describe the constancy of color measurements over different conditions and varying camera parameter settings. The color before calibration implies too severe changes in color to be associated with a biological phenomenon, as shown in Figure 10a. Although all images were collected from the same plot, the mean color intensities varied among image sessions due to the different illumination conditions and camera parameter settings. While the intensity remained more consistent after the color calibration, as presented in Figure 10b. It was also noted that the color corrected images had consistently higher green intensity than red and blue due to the high chlorophyll content at the seedling stage. While at the senescence stage, the red value is expected to be increased, as plants begin to turn yellow with decreased chlorophyll content (data was not shown here) [55]. It would be very difficult to observe such chlorophyll-related changing patterns of plants from RGB images without color calibration.

Our study focused on improving the efficiency of the color calibration process using a deep learning-based method and demonstrating its applicability in real-time series data and did not consider its implications and usefulness for typical plant phenotyping analyses since this was demonstrated in several studies [55,56]. For example, color-corrected images are useful for detecting the variations among different plant varieties or plants grown under different nitrogen concentrations, and even plants grown under inconsistent illumination conditions [57]. Also, studies have used color-corrected images to detect the senescence stage of the crops [58]. In this context, our color-corrected images could be employed to estimate oilseed rape phenotypic traits, such as yield, biomass, and chlorophyll content.

3.5. Comparison of Different Color Calibration Methods

Table 2. Comparison of the performance of different image color calibration algorithms, including our proposed framework, grey world (GW), white patch (WP), and principal component analysis (PCA). The algorithm with the best performance is highlighted in bold. N/A = not available.

Method	Mean (µ)	Median	Trimean	Best-25% (µ)	Worst-25% (µ)	Time (s)
No calibration	41.94	40.39	42.58	38.25	46.28	N/A
Proposed method	16.23	13.27	14.85	10.92	23.37	0.150
GW	35.09	33.72	34.18	27.93	42.98	0.132
WP	38.97	36.09	37.94	34.39	44.47	0.112
PCA	35.46	33.85	34.72	29.11	42.23	0.146

shows the comparison between our proposed color calibration method and the previously reported algorithms like GW, WP, and PCA, and the statistical significance by Wilcoxon signed-rank test is presented in

Table 3. Wilcoxon signed-rank test compared the performance difference of each two methods. A positive value (1) at the location (i,j) indicates the median of the method i is significantly lower than the median of method j at the 95% confidence level. A negative value (−1) indicates the opposite and zero (0) indicates there is no significant difference between the two methods.

PCA	WP	GW	Proposed
1	1	1	0	Proposed
1	1	0	−1	GW
−1	0	−1	−1	WP
0	1	−1	−1	PCA

. Although GW, WP, and PCA were fast enough in the color calibration process, their calibration errors were high. The average color errors using these methods range between 35 ΔΕ and 38 ΔΕ. While our proposed framework achieved the best performance with an accuracy of 16.23 ΔΕ, which is significantly lower than GW, WP, and PCA algorithms, the time is comparably longer than GW, WP, and PCA methods. The processing time of color calibration using GW, WP, and PCA was fast because these algorithms calibrated the color by simply scaling the color value of each pixel with a certain constant. While our calibration method was performed by using multiple steps, including classification, CCM estimation, and color correction, which takes a little bit longer but is still acceptable for real-time applications as suggested by Bosilj et al. [59], our future work will focus on improving the computation time by further reducing the learnable parameters of the CNN architecture while keeping the same level of the calibration accuracy.

4. Conclusions

In this study, we proposed an efficient deep learning framework combined with the k-means algorithm for calibrating the color of oilseed rape images. We demonstrated the potential of deep CNN for extraction of low-level features (e.g., color of the illuminant) to discriminate between images collected under different illumination conditions and using various camera parameter settings. The deep learning model achieved overall training and validation accuracies of 98.00% and 98.53%, respectively. The output of the deep CNN combined with k-means cluster centers estimated the CCM automatically. Our proposed approach outperformed previously reported methods with a mean color error of 16.23 ΔΕ, and the deep learning framework showed superior performance for rapidly calibrating images in an automated fashion in a relatively short time of 0.15 s. The proposed framework can be incorporated with any aerial- or ground-based platforms for accurately performing color calibration of RGB images to characterize the phenotypic traits of the plant consistently. Future work will be focused on exploring the capability of unsupervised deep learning methods, using a more comprehensive dataset from different crops under controlled and natural conditions, and performing color calibration on a per pixel-level.