Multi-Scale Relationship between Land Surface Temperature and Landscape Pattern Based on Wavelet Coherence: The Case of Metropolitan Beijing, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Preprocessing
2.3. Land Surface Temperature Retrieval
2.4. High Temperature Center and Landscape Metrics
2.5. Wavelet Transform and Coherency Analysis
2.5.1. Continuous Wavelet Transform
2.5.2. Wavelet Coherency Analysis
2.6. Pearson Correlation Coefficient
3. Results
3.1. Urban Land Surface Temperature Dynamics
3.1.1. High Temperature Center Variation of Different Administrative Zones
3.1.2. High Temperature Center Variation of Different Land Cover Types
3.2. Wavelet Coherency Analysis of Landscape Metrics and Land Surface Temperature
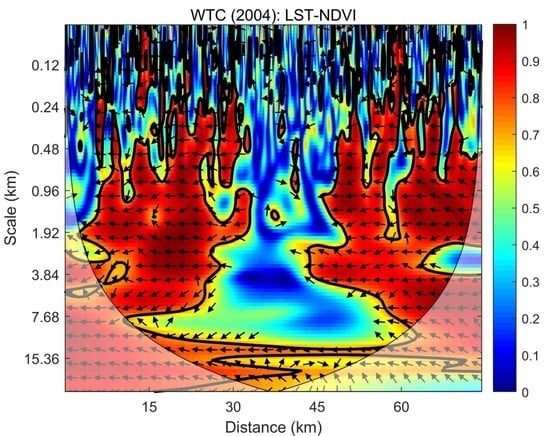
3.2.1. The Wavelet Coherencies between Landscape Composition and Land Surface Temperature
3.2.2. The Wavelet Coherencies between Landscape Configuration and Land Surface Temperature
3.3. Pearson Correlation Coefficient on Different Analysis Scales
4. Discussion
5. Conclusions
- The HTC of Beijing has a tendency to spread outwards from 2004 to 2017. In 2004, it mainly concentrated in the main urban zone and urban function extended zone, forming a spatial pattern of monocenter distribution. In 2017, the HTC gradually expanded to the new urban development zone and far suburb zone, with a spatial pattern of polycentric distribution, and gradually connected to the main urban zone and urban function extended zone, which has an adverse effect on urban LST.
- Land cover types have a significant impact on the spatial pattern of LST. The mean LST and HTC distribution of the impervious surface were the highest, while the forest land and water body were lower. Urban green space has a cooling effect on the LST, but due to its small area and scattered distribution, easily affected by the large-area impervious surface, causing the mean temperature and HTC distribution to be higher than forest land and water body.
- Wavelet coherent analysis showed that the correlation between landscape pattern metrics (landscape composition and configuration) and LST has significant multi-scale effects. The landscape composition indices NDBI and NDVI showed a correlation with LST at all scales, especially at large scales, which showed a strong positive correlation and negative correlation, respectively. The space configuration indices CONTAG, DIVISION, and LSI have no significant correlation with LST at smaller scales. With the increase of scale, it showed a strong correlation around the urban area.
- The wavelet coherence and Pearson correlation coefficients showed that the landscape composition and spatial configuration have significant effects on the LST, but the landscape composition has a greater impact on the LST in the Beijing metropolitan area.
- Totally, compared with Pearson correlation coefficient calculated by spatial rectangle sampling, the wavelet coherence diagram is smoother and less affected by the location and rectangle size, which is more conducive to describing the correlation between landscape pattern index and LST at different scales and locations.
Author Contributions
Funding
Conflicts of Interest
References
- Foster, S.S.D. The interdependence of groundwater and urbanisation in rapidly developing cities. Urban Water 2001, 3, 185–192. [Google Scholar] [CrossRef]
- Seto, K.C.; Sánchez-Rodríguez, R.; Fragkias, M. The New Geography of Contemporary Urbanization and the Environment. Annu. Rev. Environ. Resour. 2010, 35, 167–194. [Google Scholar] [CrossRef] [Green Version]
- Siswanto, S.; van Oldenborgh, G.J.; van der Schrier, G.; Jilderda, R.; van den Hurk, B. Temperature, extreme precipitation, and diurnal rainfall changes in the urbanized Jakarta city during the past 130 years. Int. J. Climatol. 2016, 36, 3207–3225. [Google Scholar] [CrossRef]
- Mander, Ü.; Kull, A.; Tamm, V.; Kuusemets, V.; Karjus, R. Impact of climatic fluctuations and land use change on runoff and nutrient losses in rural landscapes. Landsc. Urban Plan. 1998, 41, 229–238. [Google Scholar] [CrossRef]
- Luck, M.; Wu, J. A gradient analysis of urban landscape pattern: a case study from the Phoenix metropolitan region, Arizona, USA. Landsc. Ecol. 2002, 17, 327–339. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Z.; Liu, Y.; Wu, J.; Han, Y. Trend analysis of vegetation dynamics in Qinghai–Tibet Plateau using Hurst Exponent. Ecol. Indic. 2012, 14, 28–39. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhu, F.; Song, C.; Wu, J. Spatiotemporal pattern of urbanization in Shanghai, China between 1989 and 2005. Landsc. Ecol. 2013, 28, 1545–1565. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: a review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Peng, J.; Xie, P.; Liu, Y.; Ma, J. Urban thermal environment dynamics and associated landscape pattern factors: A case study in the Beijing metropolitan region. Remote Sens. Environ. 2016, 173, 145–155. [Google Scholar] [CrossRef]
- Song, J.; Du, S.; Feng, X.; Guo, L. The relationships between landscape compositions and land surface temperature: Quantifying their resolution sensitivity with spatial regression models. Landsc. Urban Plan. 2014, 123, 145–157. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, J.; He, C. A hierarchical analysis of the relationship between urban impervious surfaces and land surface temperatures: Spatial scale dependence, temporal variations, and bioclimatic modulation. Landsc. Ecol. 2016, 31, 1139–1153. [Google Scholar] [CrossRef]
- Berger, C.; Rosentreter, J.; Voltersen, M.; Baumgart, C.; Schmullius, C.; Hese, S. Spatio-temporal analysis of the relationship between 2D/3D urban site characteristics and land surface temperature. Remote Sens. Environ. 2017, 193, 225–243. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Gustafson, E.J. Quantifying Landscape Spatial Pattern: What Is the State of the Art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Du, S.; Xiong, Z.; Wang, Y.-C.; Guo, L. Quantifying the multilevel effects of landscape composition and configuration on land surface temperature. Remote Sens. Environ. 2016, 178, 84–92. [Google Scholar] [CrossRef]
- Owen, T.W.; Carlson, T.N.; Gillies, R.R. An assessment of satellite remotely-sensed land cover parameters in quantitatively describing the climatic effect of urbanization. Int. J. Remote Sens. 1998, 19, 1663–1681. [Google Scholar] [CrossRef]
- Streutker, D.R. Satellite-measured growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
- Frey, C.M.; Rigo, G.; Parlow, E. Urban radiation balance of two coastal cities in a hot and dry environment. Int. J. Remote Sens. 2007, 28, 2695–2712. [Google Scholar] [CrossRef]
- Xie, M.; Wang, Y.; Chang, Q.; Fu, M.; Ye, M. Assessment of landscape patterns affecting land surface temperature in different biophysical gradients in Shenzhen, China. Urban Ecosyst. 2013, 16, 871–886. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Sun, R.; Chen, A.; Chen, L.; Lü, Y. Cooling effects of wetlands in an urban region: The case of Beijing. Ecol. Indic. 2012, 20, 57–64. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T.L. Landscape configuration and urban heat island effects: assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Xiao, R.B.; Weng, Q.H.; Ouyang, Z.Y.; Li, W.F.; Schienke, E.W.; Zhang, Z.M. Land surface temperature variation and major factors in Beijing, China. Photogramm. Eng. Remote Sens 2008, 74, 451–461. [Google Scholar]
- Zhang, X.; Zhong, T.; Feng, X.; Wang, K. Estimation of the relationship between vegetation patches and urban land surface temperature with remote sensing. Int. J. Remote Sens. 2009, 30, 2105–2118. [Google Scholar] [CrossRef]
- Wu, J. Effects of changing scale on landscape pattern analysis: scaling relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Xu, C.; Liu, M.; Hong, C.; Chi, T.; An, S.; Yang, X. Temporal variation of characteristic scales in urban landscapes: an insight into the evolving internal structures of China’s two largest cities. Landsc. Ecol. 2012, 27, 1063–1074. [Google Scholar] [CrossRef]
- Biswas, A.; Si, B.C. Scales and locations of time stability of soil water storage in a hummocky landscape. J. Hydrol. 2011, 408, 100–112. [Google Scholar] [CrossRef]
- Guo, L.; Liu, R.; Men, C.; Wang, Q.; Miao, Y.; Zhang, Y. Quantifying and simulating landscape composition and pattern impacts on land surface temperature: A decadal study of the rapidly urbanizing city of Beijing, China. Sci. Total Environ. 2019, 654, 430–440. [Google Scholar] [CrossRef]
- Dale, M.R.T.; Mah, M. The Use of Wavelets for Spatial Pattern Analysis in Ecology. J. Veg. Sci. 1998, 9, 805–814. [Google Scholar] [CrossRef]
- Lark, R.M.; Webster, R. Analysis and elucidation of soil variation using wavelets. Eur. J. Soil Sci. 1999, 50, 185–206. [Google Scholar] [CrossRef]
- Dong, X.; Nyren, P.; Patton, B.; Nyren, A.; Richardson, J.; Maresca, T. Wavelets for Agriculture and Biology: A Tutorial with Applications and Outlook. BioScience 2008, 58, 445–453. [Google Scholar] [CrossRef] [Green Version]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin Process. Geophys 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Vadrevu, K.P.; Choi, Y. Wavelet analysis of airborne CO2 measurements and related meteorological parameters over heterogeneous landscapes. Atmos. Res. 2011, 102, 77–90. [Google Scholar] [CrossRef]
- Wu, Q.; Guo, F.; Li, H. Wavelet-Based Correlation Identification of Scales and Locations between Landscape Patterns and Topography in Urban-Rural Profiles: Case of the Jilin City, China. Remote Sens. 2018, 10, 1653. [Google Scholar] [CrossRef] [Green Version]
- Biswas, A. Landscape characteristics influence the spatial pattern of soil water storage: Similarity over times and at depths. CATENA 2014, 116, 68–77. [Google Scholar] [CrossRef]
- Saunders, S.C.; Chen, J.; Drummer, T.D.; Gustafson, E.J.; Brosofske, K.D. Identifying scales of pattern in ecological data: a comparison of lacunarity, spectral and wavelet analyses. Ecol. Complex. 2005, 2, 87–105. [Google Scholar] [CrossRef]
- Qiao, Z.; Tian, G.; Xiao, L. Diurnal and seasonal impacts of urbanization on the urban thermal environment: A case study of Beijing using MODIS data. Isprs J. Photogramm. Remote Sens. 2013, 85, 93–101. [Google Scholar] [CrossRef]
- Jiang, G.; Ma, W.; Qu, Y.; Zhang, R.; Zhou, D. How does sprawl differ across urban built-up land types in China? A spatial-temporal analysis of the Beijing metropolitan area using granted land parcel data. Cities 2016, 58, 1–9. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, L.; Sun, Z.; Meng, F.; Wang, L.; Sun, Y. Characterizing spatial and temporal trends of surface urban heat island effect in an urban main built-up area: A 12-year case study in Beijing, China. Remote Sens. Environ. 2018, 204, 826–837. [Google Scholar] [CrossRef]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Heider, D.L.; Hook, S.J.; Markham, B.L.; Chander, G.; O'Donnell, E.M. Landsat TM and ETM+ thermal band calibration. Can. J. Remote Sens 2003, 29, 141–153. [Google Scholar]
- Liu, L.; Zhang, Y. Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data: A Case Study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef] [Green Version]
- Chander, G.; Groeneveld, D.P. Intra-annual NDVI validation of the Landsat 5 TM radiometric calibration. Int. J. Remote Sens. 2009, 30, 1621–1628. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Weng, Q.; Liu, H.; Liang, B.; Lu, D. The Spatial Variations of Urban Land Surface Temperatures: Pertinent Factors, Zoning Effect, and Seasonal Variability. Ieee J. Sel. Top. Appl. Earth Obs. Remote Sens. 2008, 1, 154–166. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Azhdari, A.; Soltani, A.; Alidadi, M. Urban morphology and landscape structure effect on land surface temperature: Evidence from Shiraz, a semi-arid city. Sustain. Cities Soc. 2018, 41, 853–864. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef] [Green Version]
- Farge, M. WAVELET TRANSFORMS AND THEIR APPLICATIONS TO TURBULENCE. Annu. Rev. Fluid Mech. 1992, 24, 395–458. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
- Si, B.C.; Zeleke, T.B. Wavelet coherency analysis to relate saturated hydraulic properties to soil physical properties. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, W.; Pickett, S.T.A.; Yu, W.; Li, W. A multiscale analysis of urbanization effects on ecosystem services supply in an urban megaregion. Sci. Total Environ. 2019, 662, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Turner, B.L.; Lambin, E.F.; Reenberg, A. The emergence of land change science for global environmental change and sustainability. Proc. Natl. Acad. Sci. 2007, 104, 20666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taha, H. Urban climates and heat islands: albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Qi, Z.-F.; Ye, X.-Y.; Cai, Y.-B.; Ma, W.-C.; Chen, M.-N. Analysis of land use/land cover change, population shift, and their effects on spatiotemporal patterns of urban heat islands in metropolitan Shanghai, China. Appl. Geogr. 2013, 44, 121–133. [Google Scholar] [CrossRef]
- Dissanayake, D.; Morimoto, T.; Ranagalage, M.; Murayama, Y. Land-Use/Land-Cover Changes and Their Impact on Surface Urban Heat Islands: Case Study of Kandy City, Sri Lanka. Climate 2019, 7, 99. [Google Scholar] [CrossRef] [Green Version]








| Sensor | Scene ID | Acquisition Data | Season |
|---|---|---|---|
| Landsat-5 TM | LT51230322004252BJC00 | 8 September 2004 | Summer |
| Landste-8 OLI/TIRS | LC81230322017255LGN00 | 12 September 2017 | Summer |
| Types | Bare Land | Water | Urban Green Space | Cultivated Land | Forest Land | Impervious Surface | User’s Accuracy |
|---|---|---|---|---|---|---|---|
| 2004 | |||||||
| Bare land | 285 | 0 | 0 | 7 | 47 | 8 | 82.13% |
| Water | 0 | 719 | 7 | 16 | 117 | 23 | 81.53% |
| Urban green space | 0 | 8 | 563 | 23 | 86 | 17 | 80.77% |
| Cultivated land | 19 | 9 | 13 | 7513 | 1836 | 49 | 79.60% |
| Forest land | 30 | 76 | 43 | 1525 | 16,077 | 580 | 87.70% |
| Impervious surface | 9 | 15 | 6 | 76 | 947 | 3847 | 78.51% |
| Producer’s accuracy | 83.09% | 86.94% | 89.08% | 82.02% | 84.13% | 85.04% | |
| OA: 83.84% Kappa coefficient: 0.737 | |||||||
| 2017 | |||||||
| Bare land | 535 | 0 | 5 | 6 | 83 | 16 | 82.95% |
| Water | 0 | 590 | 9 | 10 | 96 | 24 | 80.93% |
| Urban green space | 0 | 3 | 747 | 37 | 117 | 13 | 81.46% |
| Cultivated land | 56 | 55 | 15 | 5193 | 963 | 69 | 81.77% |
| Forest land | 34 | 31 | 43 | 668 | 14,452 | 1144 | 88.27% |
| Impervious surface | 23 | 24 | 17 | 192 | 1483 | 7843 | 81.85% |
| Producer’s accuracy | 82.56% | 83.93% | 89.35% | 85.05% | 84.05% | 86.10% | |
| OA: 84.87% Kappa coefficient: 0.770 | |||||||
| Type | Metrics | Formula | Instructions |
|---|---|---|---|
| Landscape Composition | Normalized Difference Built-up Index (NDBI) | A measure of the abundance of built-up area in the landscape. Band 4 and 5 of Landsat TM sensor, Band 5 and 6 of Landsat OIL sensor. | |
| Normalized Difference Vegetation Index (NDVI) | A measure of the abundance of vegetation in the landscape. Band 3 and 4 of Landsat TM sensor, Band 4 and 5 of Landsat OIL sensor. | ||
| Shannon Diversity Index (SHDI) | equals the plane area of class i, divided by the landscape area. | ||
| Landscape Spatial Configuration | Contagion Index (CONTAG) | The contagion index refers to the non-random or aggregation degree of patch types in the landscape. Additionally, a larger metric value means larger aggregation degree, conversely lower. | |
| Landscape Division Index (DIVISION) | A measure of the fragmentation of land covers. DIVISION deals with the degree to which the landscape is broken up into separate patches. | ||
| Landscape Shape Index (LSI) | Landscape shape index refers to the deviation degree between the real shape of patch and the circle or square with the same area, indicating the complexity of landscape. |
| Zone 1 | Year | Mean LST (°C) | Percentage of HTC | DI |
|---|---|---|---|---|
| MUZ | 2004 | 34.92 | 85.91% | 6.96 |
| 2017 | 34.13 | 84.70% | 6.17 | |
| UFEZ | 2004 | 31.61 | 58.12% | 4.71 |
| 2017 | 32.01 | 49.94% | 3.64 | |
| NUDZ | 2004 | 28.23 | 17.49% | 1.42 |
| 2017 | 29.86 | 20.03% | 1.46 | |
| FSZ | 2004 | 24.35 | 1.96% | 0.16 |
| 2017 | 26.32 | 3.07% | 0.22 | |
| Beijing | 2004 | 26.21 | 12.34% | - |
| 2017 | 27.88 | 13.72% | - |
| Landscape Type | Year | Mean LST (°C) | Percentage of HTC | DI |
|---|---|---|---|---|
| Impervious surface | 2004 | 31.08 | 53.74% | 4.35 |
| 2017 | 31.84 | 47.39% | 3.45 | |
| Bare land | 2004 | 28.36 | 12.30% | 1.92 |
| 2017 | 27.74 | 9.71% | 1.26 | |
| Cultivated land | 2004 | 27.66 | 12.67% | 1.03 |
| 2017 | 29.21 | 11.96% | 0.87 | |
| Urban green space | 2004 | 28.74 | 24.04% | 1.95 |
| 2017 | 28.19 | 7.79% | 1.17 | |
| Water | 2004 | 26.64 | 12.34% | 0.86 |
| 2017 | 27.09 | 5.22% | 0.38 | |
| Forest | 2004 | 24.29 | 23.08% | 0.19 |
| 2017 | 25.68 | 1.01% | 0.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Tan, J.; Guo, F.; Li, H.; Chen, S. Multi-Scale Relationship between Land Surface Temperature and Landscape Pattern Based on Wavelet Coherence: The Case of Metropolitan Beijing, China. Remote Sens. 2019, 11, 3021. https://doi.org/10.3390/rs11243021
Wu Q, Tan J, Guo F, Li H, Chen S. Multi-Scale Relationship between Land Surface Temperature and Landscape Pattern Based on Wavelet Coherence: The Case of Metropolitan Beijing, China. Remote Sensing. 2019; 11(24):3021. https://doi.org/10.3390/rs11243021
Chicago/Turabian StyleWu, Qiong, Jinxiang Tan, Fengxiang Guo, Hongqing Li, and Shengbo Chen. 2019. "Multi-Scale Relationship between Land Surface Temperature and Landscape Pattern Based on Wavelet Coherence: The Case of Metropolitan Beijing, China" Remote Sensing 11, no. 24: 3021. https://doi.org/10.3390/rs11243021
APA StyleWu, Q., Tan, J., Guo, F., Li, H., & Chen, S. (2019). Multi-Scale Relationship between Land Surface Temperature and Landscape Pattern Based on Wavelet Coherence: The Case of Metropolitan Beijing, China. Remote Sensing, 11(24), 3021. https://doi.org/10.3390/rs11243021