Atmospheric Correction of OLCI Imagery over Extremely Turbid Waters Based on the Red, NIR and 1016 nm Bands and a New Baseline Residual Technique
Abstract
:1. Introduction
- P1.
- P2.
- P3.
- Top of atmosphere (TOA) reflectance may even exceed the photodetector saturation values of certain ocean colour sensors rendering these wavelengths unusable (Dogliotti et al., 2011 [8]).
2. Materials and Methods
2.1. In Situ Radiometric Measurements
2.2. Radiative Transfer Simulations
2.3. Ocean and Land Colour Instrument (OLCI) Imagery
2.4. Algorithm Theoretical Basis
2.5. Band Choice
2.6. Transmittance Factor Treatment
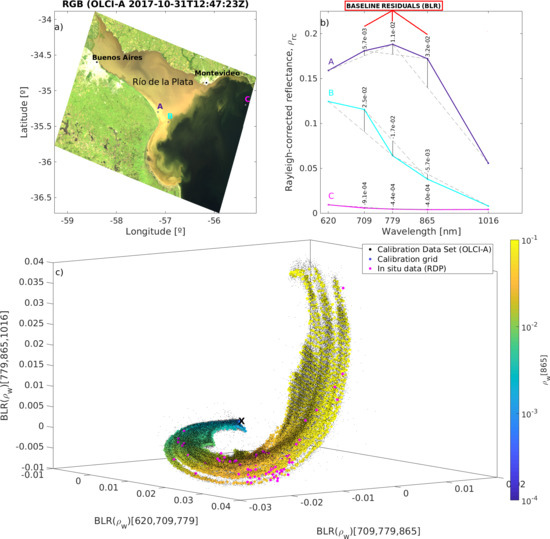
2.7. Relation between Baseline Residuals and Water Reflectances
2.8. Estimation of Aerosol Reflectance at Bands 865 nm and 1016 nm
2.9. Atmospheric Correction Scheme: Summary
- The PPE correction (Gossn 2018 [34]) is applied on L1B imagery (TOA radiances).
- Rayleigh (and gaseous absorption) correction is applied using SeaDAS v7.5 software.
- , and are computed from the corresponding Rayleigh-corrected reflectances (see Section 2.4 and Section 2.5, Equation (5)).
- A transmittance factor correction is applied to relate with (see Section 2.6, Equation (13)).
- For each pixel, the computed BLRs are matched to the BLRs from the calibration surface that minimize the Euclidean distance in BLR space. The corresponding water reflectance at 865 nm and 1016 nm is assigned to the pixel (see Section 2.7).
- The atmospheric residual at these bands is obtained by subtracting the assigned water signal to the RC reflectance (see Section 2.8, Equation (16)).
- A final constraint is applied to to limit inside the reasonable range of (see Section 2.8, Equation (17)).
3. Results
3.1. Baseline Residuals in Clear and Turbid Waters
3.2. Atmospheric Correction Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BL | Baseline term |
| BLR | Baseline Residual |
| BLR-AC | Baseline Residual Atmospheric Correction Scheme |
| CCD | Charged-Coupled Devices |
| CNES-SOS | Centre National d’Études Spatiales-Successive Orders of Scattering |
| CODA | Copernicus Online Data Access |
| ESA | European Space Agency |
| FAI | Floating Algal Index |
| Fix-AC | Fix Clear Window Atmospheric Correction Scheme |
| FLH | Fluorescence Line Height |
| HICO | Hyperspectral Imager for the Coastal Ocean |
| IOP | Inherent Optical Property |
| MCI | Maximum Chlorophyll Index |
| MERIS | MEdium Resolution Imaging Spectrometer |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NASA | National Aeronautics and Space Administration |
| NIR | Near Infra-Red |
| OBPG | Ocean Biology Processing Group |
| OLCI | Ocean and Land Colour Instrument |
| PPE | Prompt Particle Event |
| CHRIS/PROBA | Compact High Resolution Imaging Spectrometer/Project for On-Board Autonomy |
| qSSA | quasi-Single Scattering Approximation |
| RC | Rayleigh-corrected |
| RNS | Red-NIR-SWIR |
| SABIA-Mar | Satélite Argentino-Brasileño para la Información del Mar |
| SPM | Suspended Particulate Matter |
| SWIR | Short-Wave-Infra-Red |
| TOA | Top of atmosphere |
| WMO | World Meteorological Organization |
Appendix A. Quasi-Single Scattering Approximation Reflectance Model
References
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.; Arnone, R.; Gould, R.; Martinolich, P.M.; Ransibrahmanakul, V. A partially coupled ocean-atmosphere model for retrieval of water-leaving radiance from SeaWiFS in coastal waters. NASA Tech. Memo 2003, 206892, 51–59. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Ruddick, K.; Vanhellement, Q. Use of OLCI and SLSTR Bands for Atmospheric Correction over Turbid Coastal and Inland Waters. In Proceedings of the Sentinel-3 for Science Workshop, Casinò, Italy, 2–5 June 2015; Volume 734, p. 55. [Google Scholar]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Shang, S.; Lin, G.; Chen, J.; Doxaran, D. On the modeling of hyperspectral remote-sensing reflectance of high-sediment-load waters in the visible to shortwave-infrared domain. Appl. Opt. 2016, 55, 1738–1750. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Doxaran, D.; Ruddick, K.; Shen, F.; Gentili, B.; Yan, L.; Huang, H. Saturation of water reflectance in extremely turbid media based on field measurements, satellite data and bio-optical modelling. Opt. Express 2018, 26, 10435–10451. [Google Scholar] [CrossRef]
- Dogliotti, A.; Ruddick, K.; Nechad, B.; Lasta, C. Improving Water Reflectance Retrieval from MODIS Imagery in the Highly Turbid Waters of La Plata River. In Proceedings of the VI International Conference: Current Problems in Optics of Natural Waters (ONW 2011), St. Petersburg, Russia, 6–10 September 2011; p. 152. [Google Scholar]
- Wang, M.; Shi, W. Estimation of ocean contribution at the MODIS near-infrared wavelengths along the east coast of the US: Two case studies. Geophys. Res. Lett. 2005, 32, L13606. [Google Scholar] [CrossRef]
- Knaeps, E.; Dogliotti, A.I.; Raymaekers, D.; Ruddick, K.; Sterckx, S. In situ evidence of non-zero reflectance in the OLCI 1020nm band for a turbid estuary. Remote Sens. Environ. 2012, 120, 133–144. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Chomko, M.; Gordon, H. Atmospheric Correction of Ocean Color Imagery: Test of the Spectral Optimization Algorithm with the Sea-Viewing Wide Field-of-View Sensor. Appl. Opt. 2001, 40, 2973–2984. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Philpot, W. The derivative ratio algorithm: Avoiding atmospheric effects in remote sensing. IEEE Trans. Geosci. Remote Sens. 1991, 29, 350–357. [Google Scholar] [CrossRef]
- Letelier, R.; Abbott, M. An analysis of chlorophyll fluorescence algorithms for the Moderate Resolution Imaging Spectrometer (MODIS). Remote Sens. Environ. 1996, 58, 215–223. [Google Scholar] [CrossRef]
- Dogliotti, A.; Ruddick, K.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef] [Green Version]
- Dogliotti, A.; Ruddick, K.; Guerrero, R. Seasonal and inter-annual turbidity variability in the Río de la Plata from 15 years of MODIS: El Niño dilution effect. Estuar. Coast. Shelf Sci. 2016, 182, 27–39. [Google Scholar] [CrossRef] [Green Version]
- Nechad, B.; Ruddick, K.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.X.; Li, D.J.; Zhu, W.J.; Salama, M. Medium resolution imaging spectrometer (MERIS) estimation of chlorophyll-a concentration in the turbid sediment-laden waters of the Changjiang (Yangtze) Estuary. Int. J. Remote Sens. 2010, 31, 4635–4650. [Google Scholar] [CrossRef]
- Moreira, D.; Simionato, C.; Gohin, F.; Cayocca, F.; Luz Clara, M. Suspended matter mean distribution and seasonal cycle in the Rio de La Plata estuary and the adjacent shelf from ocean color satellite (MODIS) and in-situ observations. Cont. Shelf Res. 2013, 68, 51–66. [Google Scholar] [CrossRef]
- Gilerson, A.A.; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S.A. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar] [CrossRef]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Gons, H.J.; Rijkeboer, M.; Ruddick, K.G. Effect of a waveband shift on chlorophyll retrieval from MERIS imagery of inland and coastal waters. J. Plankton Res. 2005, 27, 125–127. [Google Scholar] [CrossRef]
- Framiñan, M.; Brown, O. Study of the Río de la Plata turbidity front, Part 1: Spatial and temporal distribution. Cont. Shelf Res. 1996, 16, 1259–1282. [Google Scholar] [CrossRef]
- Mueller, L.J.; Morel, A.; Frouin, R.; Davis, C.; Arnone, R.; Carder, K.; Li, Z.; Steward, R.; Hooker, S.; Mobley, C.; et al. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume III: Radiometric Measurements and Data Analysis Protocols; Technical Report NASA/TM-2003-21621/Rev-Vol III; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003.
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Lenoble, J.; Herman, M.; Deuzé, J.L.; Lafrance, B.; Santer, R.; Tanré, D. A successive order of scattering code for solving the vector equation of transfer in the earth’s atmosphere with aerosols. J. Quant. Spectrosc. Radiat. Transf. 2007, 107, 479–507. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Programme, W.C.R. A Preliminary Cloudless Standard Atmosphere for Radiation Computation; Technical Report WMO/TD, no. 24.; WCP (Series), 112; International Association of Meteorology and Atmospheric Physics: Boulder, CO, USA, 1986. [Google Scholar]
- Bodhaine, B.A.; Slusser, J.R. On Rayleigh Optical Depth Calculations. J. Atmos. Ocean. Technol. 1999, 16, 1854–1861. [Google Scholar] [CrossRef]
- Mobley, C.; Werdell, J.; Franz, B.; Ahmad, Z.; Bailey, S. Atmospheric Correction for Satellite Ocean Color Radiometry; Technical report; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2016.
- Copernicus Online Data Access. EUMETSAT. Available online: coda.eumetsat.int (accessed on 1 February 2018).
- S3 Mission Performance Centre (2017), Sentinel-3 Product Notice S3A.PN-OLCI-L2L.02, Issue/Rev Date 06/11/2017. Available online: sentinel.esa.int/documents/247904/2702575/Sentinel-3-OLCI-Product-Notice-Level-2-Land (accessed on 20 November 2017).
- Gossn, J.I. Effect of Prompt Particle Events on OLCI Ocean Color Imagery in the South Atlantic Anomaly: Detection and Removal. IEEE Geosci. Remote Sens. Lett. 2018. [Google Scholar] [CrossRef]
- D’Amico, G.; Corsini, M.D.; Nieke, J. Prompt-Particle-Events in ESA’s Envisat/MERIS and Sentinel-3/OLCI Data: Observations, Analysis and Recommendations. Master’s Thesis, University of Pisa, Pisa, Italy, 2015. [Google Scholar]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef]
- Antoine, D.; Morel, A. A multiple scattering algorithm for atmospheric correction of remotely sensed ocean colour (MERIS instrument): Principle and implementation for atmospheres carrying various aerosols including absorbing ones. Int. J. Remote Sens. 1999, 20, 1875–1916. [Google Scholar] [CrossRef]
- Moore, G.F.; Aiken, J.; Lavender, S.J. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: Application to MERIS. Int. J. Remote Sens. 1999, 20, 1713–1733. [Google Scholar] [CrossRef]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Gower, J.; King, S. Distribution of floating Sargassum in the Gulf of Mexico and the Atlantic Ocean mapped using MERIS. Int. J. Remote Sens. 2011, 32, 1917–1929. [Google Scholar] [CrossRef]
- Shettle, E.; Fenn, R. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on their Optical Properties. Environ. Res. Pap. 1979, 676, 1–94. [Google Scholar]
- European Space Agency, Sentinel Online. S3-OLCI Document Library: Sentinel-3 OLCI-A Spectral Response Functions. Available online: sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-olci/olci-instrument/spectral-response-function-data (accessed on 11 December 2017).
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light scattering properties of marine particles in coastal and open ocean waters as related to the particle mass concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef] [Green Version]
- Babin, M.; Stramski, D.; Ferrari, G.M.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. 2003, 108, 3211–3231. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Tang, J.; Wang, D. Atmospheric correction of satellite ocean color imagery using the ultraviolet wavelength for highly turbid waters. Opt. Express 2012, 20, 20754–20770. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef]
- Loisel, H.; Morel, A. Non-isotropy of the upward radiance field in typical coastal (Case 2) waters. Int. J. Remote Sens. 2001, 22, 275–295. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. III. Implication of bidirectionality for the remote-sensing problem. Appl. Opt. 1996, 35, 4850–4862. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]














| CNES-SOS Parameter | Input Values |
|---|---|
| (Wavelength) | 615–1040 nm (step 5 nm) |
| (Solar zenith angle) | 0°–60° (step 30°) |
| (Viewing zenith angle) | 0°–60° (step 30°) |
| (Relative azimuth angle) | 0°–180° (step 45°) |
| (Water reflectance) | ASD in situ (RdP) |
| W (Wind speed) | 3 m/s |
| (Relative air-water refractive index) | 1.334 |
| (Rayleigh optical thickness) | Bodhaine et al., 1999 [30] |
| (Molecular depolarization factor) | Bodhaine et al., 1999 [30] |
| (Molecular e-folding height) | 8 km |
| (Aerosol optical thickness at 500 nm) | 0:0.1:0.4 |
| / (Aerosol granulometry) | WMO-C, -M, -U [29] |
| (Aerosol e-folding height) | 2 km |
| (Maximum scattering order) | 20 |
| (Polarization flag) | 1 (consider polarization) |
| Region | Aquisition Date-Time | Calibration/Validation Window (s) | Fix Window Atmospheric Correction (Fix-AC) Window | Cal/Val |
|---|---|---|---|---|
| yyyy-mm-ddThh:mm:ssZ | lines; pixels | lines; pixels | Cal | |
| RdP | 2016-08-17T12:55:02Z | 1347–1636; 1258–1528 | 1750–1764; 1143–1157 | Cal |
| RdP | 2016-11-10T12:51:59Z | 1057–1446; 521–685 | 1598–1612; 567–581 | Cal |
| RdP | 2016-11-29T12:58:49Z | 1643–1796; 1218–1332 | 2117–2131; 1267–1281 | Cal |
| RdP | 2017-01-14T13:06:26Z | 2254–2589; 838–1052 | 2655–2669; 1155–1169 | Cal |
| RdP | 2017-03-13T13:02:29Z | 1890–2013; 1177–1258 2044–2124; 1130–1256 | 2140–2154; 1462–1476 | Cal |
| RdP | 2017-05-01T13:32:08Z | 4301–4525; 1126–1177 4381–4561; 1216–1356 | 4549–4563; 1271–1285 | Cal |
| RdP | 2017-07-02T13:24:47Z | 3761–3840; 1220–1254 | 4133–4147; 1498–1512 | Cal |
| RdP | 2017-10-15T13:02:34Z | 1586–1927; 1088–1182 | 2460–2474; 1635–1649 | Cal |
| RdP | 2017-11-19T12:54:31Z | 1355–1576; 2252–2366 1367–1718; 2108–2247 862–1262; 2025–2108 | 1895–1909; 2178–2192 | Cal |
| BE | 2016-07-19T10:00:32Z | 1613–1823; 1525–1649 | 1497–1511; 1790–1804 | Val |
| BBl | 2016-10-09T13:22:33Z | 2359–2701; 970–1094 | 2917–2931; 1077–1091 | Val |
| RdP | 2017-10-31T12:47:47Z | 724–927; 1398–1452 | 1104–1118; 1774–1788 | Val |
| RdP | 2017-01-21T13:24:42Z | Full RdP | Not applied | Val |
| RdP | 2016-06-08T13:09:51Z | Full RdP | Not applied | Val |
| RdP | 2017-12-12T12:59:01Z | Full RdP | Not applied | Val |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gossn, J.I.; Ruddick, K.G.; Dogliotti, A.I. Atmospheric Correction of OLCI Imagery over Extremely Turbid Waters Based on the Red, NIR and 1016 nm Bands and a New Baseline Residual Technique. Remote Sens. 2019, 11, 220. https://doi.org/10.3390/rs11030220
Gossn JI, Ruddick KG, Dogliotti AI. Atmospheric Correction of OLCI Imagery over Extremely Turbid Waters Based on the Red, NIR and 1016 nm Bands and a New Baseline Residual Technique. Remote Sensing. 2019; 11(3):220. https://doi.org/10.3390/rs11030220
Chicago/Turabian StyleGossn, Juan Ignacio, Kevin George Ruddick, and Ana Inés Dogliotti. 2019. "Atmospheric Correction of OLCI Imagery over Extremely Turbid Waters Based on the Red, NIR and 1016 nm Bands and a New Baseline Residual Technique" Remote Sensing 11, no. 3: 220. https://doi.org/10.3390/rs11030220
APA StyleGossn, J. I., Ruddick, K. G., & Dogliotti, A. I. (2019). Atmospheric Correction of OLCI Imagery over Extremely Turbid Waters Based on the Red, NIR and 1016 nm Bands and a New Baseline Residual Technique. Remote Sensing, 11(3), 220. https://doi.org/10.3390/rs11030220