A Recursive Update Model for Estimating High-Resolution LAI Based on the NARX Neural Network and MODIS Times Series
Abstract
:1. Introduction
2. Methods
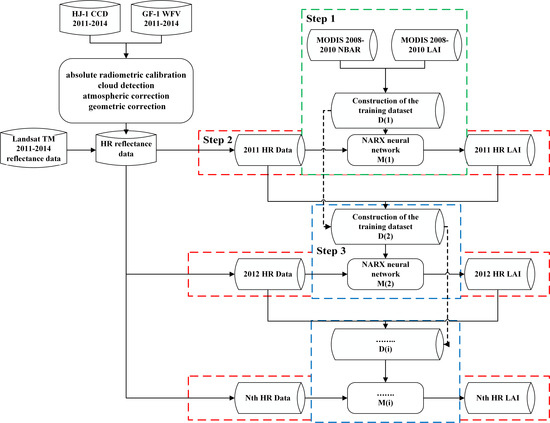
2.1. Recursive Update Model
2.2. Application of the NARX Network
3. Materials
3.1. Study Area
3.2. Field Data
3.3. Satellite Image Pre-Processing
3.3.1. HR Reflectance Data
3.3.2. MCD43A4 NBAR Product
3.3.3. MCD15A2 LAI Product
3.3.4. Surface Reflectance Normalization
4. Results
4.1. 2013 and 2014 LAI Estimations from Satellite Data
4.2. Regional LAI Estimation
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Black, T. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Hernández, C.; Nunes, L.; Lopes, D.; Graña, M. Data fusion for high spatial resolution lai estimation. Inf. Fusion 2014, 16, 59–67. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V. Albedo and lai estimates from formosat-2 data for crop monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Chern, J.-S.; Wu, A.-M.; Lin, S.-F. Lesson learned from formosat-2 mission operations. Acta Astronaut. 2006, 59, 344–350. [Google Scholar] [CrossRef]
- Pu, R.; Cheng, J. Mapping forest leaf area index using reflectance and textural information derived from worldview-2 imagery in a mixed natural forest area in Florida, US. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 11–23. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental sentinel-2 lai estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Novelli, A.; Tarantino, E.; Fratino, U.; Iacobellis, V.; Romano, G.; Gentile, F. A data fusion algorithm based on the kalman filter to estimate leaf area index evolution in durum wheat by using field measurements and modis surface reflectance data. Remote Sens. Lett. 2016, 7, 476–484. [Google Scholar] [CrossRef]
- Eklundh, L.; Hall, K.; Eriksson, H.; Ardö, J.; Pilesjö, P. Investigating the use of landsat thematic mapper data for estimation of forest leaf area index in southern sweden. Can. J. Remote Sens. 2003, 29, 349–362. [Google Scholar] [CrossRef]
- Baret, F.; Clevers, J.; Steven, M. The robustness of canopy gap fraction estimates from red and near-infrared reflectances: A comparison of approaches. Remote Sens. Environ. 1995, 54, 141–151. [Google Scholar] [CrossRef]
- Walthall, C.; Dulaney, W.; Anderson, M.; Norman, J.; Fang, H.; Liang, S. A comparison of empirical and neural network approaches for estimating corn and soybean leaf area index from landsat etm+ imagery. Remote Sens. Environ. 2004, 92, 465–474. [Google Scholar] [CrossRef]
- Potithep, S.; Nasahara, K.; Muraoka, H.; Nagai, S.; Suzuki, R. What is the actual relationship between lai and vi in a deciduous broadleaf forest? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 609–614. [Google Scholar]
- Fan, L.; Gao, Y.; Brück, H.; Bernhofer, C. Investigating the relationship between ndvi and lai in semi-arid grassland in inner mongolia using in-situ measurements. Theor. Appl. Climatol. 2009, 95, 151–156. [Google Scholar] [CrossRef]
- Lee, B.; Kwon, H.; Miyata, A.; Lindner, S.; Tenhunen, J. Evaluation of a phenology-dependent response method for estimating leaf area index of rice across climate gradients. Remote Sens. 2016, 9, 20. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation lai and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C. Inversion of a forest reflectance model to estimate structural canopy variables from hyperspectral remote sensing data. Remote Sens. Environ. 2006, 100, 281–294. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for lai mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnere, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Pan, J. Retrieve leaf area index from hj-ccd image based on support vector regression and physical model. Proc. SPIE 2013, 8887, 88871R. [Google Scholar]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating leaf area index (lai) at multiple spatial scales through lidar remote sensing: A case study in sierra national forest, ca. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Qin, J.; Qu, Y. An upscaling algorithm to obtain the representative ground truth of lai time series in heterogeneous land surface. Remote Sens. 2015, 7, 12887–12908. [Google Scholar] [CrossRef]
- Danson, F.M.; Rowland, C.S.; Baret, F. Training a neural network with a canopy reflectance model to estimate crop leaf area index. Int. J. Remote Sens. 2003, 24, 4891–4905. [Google Scholar] [CrossRef]
- Noble, P.A.; Tribou, E.H. Neuroet: An easy-to-use artificial neural network for ecological and biological modeling. Ecol. Model. 2007, 203, 87–98. [Google Scholar] [CrossRef]
- Li, Z.; Fox, J.M. Integrating mahalanobis typicalities with a neural network for rubber distribution mapping. Remote Sens. Lett. 2011, 2, 157–166. [Google Scholar] [CrossRef]
- Shupe, S.M.; Marsh, S.E. Cover-and density-based vegetation classifications of the sonoran desert using landsat tm and ers-1 sar imagery. Remote Sens. Environ. 2004, 93, 131–149. [Google Scholar] [CrossRef]
- Jensen, J.; Qiu, F.; Ji, M. Predictive modelling of coniferous forest age using statistical and artificial neural network approaches applied to remote sensor data. Int. J. Remote Sens. 1999, 20, 2805–2822. [Google Scholar]
- Muukkonen, P.; Heiskanen, J. Estimating biomass for boreal forests using aster satellite data combined with standwise forest inventory data. Remote Sens. Environ. 2005, 99, 434–447. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of lai, fapar, fcover and lai×cab, from top of canopy meris reflectance data: Principles and validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S. Retrieving leaf area index with a neural network method: Simulation and validation. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2052–2062. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S. A hybrid inversion method for mapping leaf area index from modis data: Experiments and application to broadleaf and needleleaf canopies. Remote Sens. Environ. 2005, 94, 405–424. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the landsat and modis surface reflectance: Predicting daily landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Liu, Y.; Wang, X.; Liu, Y. Asynchronous harmonic analysis based on out-of-sequence measurement for large-scale residential power network. In Proceedings of the Instrumentation and Measurement Technology Conference, Pisa, Italy, 11–14 May 2015; pp. 1693–1698. [Google Scholar]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetan, G.B.; Talebi, H.A. Nonlinear load sharing and voltage compensation of microgrids based on harmonic power-flow calculations using radial basis function neural networks. IEEE Syst. J. 2016, PP, 1–11. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (narx). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Sauter, T.; Weitzenkamp, B.; Schneider, C. Spatio-temporal prediction of snow cover in the black forest mountain range using remote sensing and a recurrent neural network. Int. J. Climatol. 2010, 30, 2330–2341. [Google Scholar] [CrossRef]
- Chai, L.; Qu, Y.; Zhang, L.; Liang, S.; Wang, J. Estimating time-series leaf area index based on recurrent nonlinear autoregressive neural networks with exogenous inputs. Int. J. Remote Sens. 2012, 33, 5712–5731. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in narx recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar] [PubMed]
- Demuth, H.; Beale, M. Neural Network Toolbox for Use with Matlab; Mathworks Inc.: Natick, MA, USA, 1992; p. 355. [Google Scholar]
- Qu, Y.; Han, W.; Fu, L.; Li, C.; Song, J.; Zhou, H.; Bo, Y.; Wang, J. Lainet—A wireless sensor network for coniferous forest leaf area index measurement: Design, algorithm and validation. Comput. Electron. Agric. 2014, 108, 200–208. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Y.; Han, W.; Wang, J.; Ma, M. Crop leaf area index observations with a wireless sensor network and its potential for validating remote sensing products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 431–444. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, J.; Qu, Y. A prior knowledge-based method to derivate high-resolution leaf area index maps with limited field measurements. Remote Sens. 2016, 9, 13. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.K. A landsat surface reflectance dataset for north america, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: an overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the landsat 8/oli land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Sun, L.; Wei, J.; Bilal, M.; Tian, X.; Jia, C.; Guo, Y.; Mi, X. Aerosol optical depth retrieval over bright areas using landsat 8 oli images. Remote Sens. 2015, 8, 23. [Google Scholar] [CrossRef]
- Sun, L.; Sun, C.; Liu, Q.; Zhong, B. Aerosol optical depth retrieval by hj-1/ccd supported by modis surface reflectance data. Sci. China Earth Sci. 2010, 53, 74–80. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P. First operational brdf, albedo nadir reflectance products from modis. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R. Global products of vegetation leaf area and fraction absorbed par from year one of modis data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Yang, W.; Huang, D.; Tan, B.; Stroeve, J.C.; Shabanov, N.V.; Knyazikhin, Y.; Nemani, R.R.; Myneni, R.B. Analysis of leaf area index and fraction of par absorbed by vegetation products from the terra modis sensor: 2000–2005. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1829–1842. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of modis lai/fpar product collection 6. Part 2: Validation and intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize landsat reflectance data to nadir brdf adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Vermote, E.; Vermeulen, A. Atmospheric Correction Algorithm: Spectral Reflectances (mod09), Algorithm Theoretical Background Document. 1999; version 4.0. Available online: https://lpdaac.usgs.gov/sites/default/files/public/product_documentation/atbd_mod09.pdf (accessed on 28 January 2019).
- Descloitres, J.; Vermote, E. Operational retrieval of the spectral surface reflectance and vegetation index at global scale from seawifs data. International Conference on Aerosols, Radiation Budget–Land Surfaces–Ocean Colour: The Contribution of POLDER and New Generation Spaceborne Sensors to Global Change Studies; Land Surfaces-O-02; CNES: Meribel, France; Toulouse, France, 1999; pp. 1–4.
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal modis–landsat data fusion for relative radiometric normalization, gap filling, and prediction of landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Li, F.; Jupp, D.L.B.; Reddy, S.; Lymburner, L.; Mueller, N.; Tan, P.; Islam, A. An evaluation of the use of atmospheric and brdf correction to standardize landsat data. IEEE J. Sel. Top. Appl. Earth Obs.Remote Sens. 2010, 3, 257–270. [Google Scholar] [CrossRef]
- Feng, G.; Tao, H.; Masek, J.; Shuai, Y.; Wang, Z. Angular effects and correction for medium resolution sensors to support crop monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4480–4489. [Google Scholar]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B. Validation and intercomparison of global leaf area index products derived from remote sensing data. J. Geophys. Res. Biogeosci. 2015, 113. [Google Scholar] [CrossRef]










| Data | Band | Spectral (nm) | Spatial (m) | Temporal (day) | Year | Images for Huailai |
|---|---|---|---|---|---|---|
| HJ-1 CCD | Red | 630–690 | 30 | 4 | 2011 | 31 |
| 2012 | 25 | |||||
| NIR | 760–900 | 2013 | 40 | |||
| 2014 | 26 | |||||
| GF-1 WFV | Red | 630–690 | 16 | 2 | 2013 | 9 |
| NIR | 770–890 | 2014 | 8 | |||
| Landsat 5 TM | Red | 630–690 | 30 | 16 | 2011 | 7 |
| NIR | 760–900 | |||||
| Landsat 7 ETM+ | Red | 630–690 | 30 | 16 | 2012 | 6 |
| NIR | 770–900 | |||||
| Landsat 8 OLI | Red | 640–670 | 30 | 16 | 2013 | 6 |
| NIR | 850–880 | 2014 | 8 | |||
| MCD43A4 | Red | 620–670 | 500 | 8 | 2008 | 12 |
| 2009 | 12 | |||||
| NIR | 841–876 | |||||
| 2010 | 12 | |||||
| MCD15A2 | - | - | 500 | 8 | 2008 | 12 |
| 2009 | 12 | |||||
| 2010 | 12 |
| Parameter Description | Parameter Name | Range |
|---|---|---|
| geometrical conditions | Solar zenith angle | 20–60 (°) |
| Satellite zenith angle | 20–60 (°) | |
| Relative azimuth angle | 0–180 (°) | |
| atmospheric model | Midlatitude summer | - |
| Midlatitude winter | - | |
| aerosol model | continental model | - |
| urban model | - | |
| aerosol optical depth | aerosol optical depth at 550 | 0–1 |
| reflectance | TOA | 0–0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, J.; Shi, Y.; Zhou, H.; Liao, L. A Recursive Update Model for Estimating High-Resolution LAI Based on the NARX Neural Network and MODIS Times Series. Remote Sens. 2019, 11, 219. https://doi.org/10.3390/rs11030219
Wang J, Wang J, Shi Y, Zhou H, Liao L. A Recursive Update Model for Estimating High-Resolution LAI Based on the NARX Neural Network and MODIS Times Series. Remote Sensing. 2019; 11(3):219. https://doi.org/10.3390/rs11030219
Chicago/Turabian StyleWang, Jian, Jindi Wang, Yuechan Shi, Hongmin Zhou, and Limin Liao. 2019. "A Recursive Update Model for Estimating High-Resolution LAI Based on the NARX Neural Network and MODIS Times Series" Remote Sensing 11, no. 3: 219. https://doi.org/10.3390/rs11030219
APA StyleWang, J., Wang, J., Shi, Y., Zhou, H., & Liao, L. (2019). A Recursive Update Model for Estimating High-Resolution LAI Based on the NARX Neural Network and MODIS Times Series. Remote Sensing, 11(3), 219. https://doi.org/10.3390/rs11030219