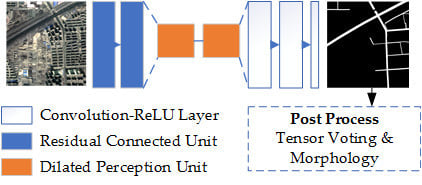
In this section, the proposed framework for extracting roads in high-resolution imagery is illustrated. The method does not require any preprocessing stage. First, the RDRCNN architecture and basic unit framework are discussed. Second, a tensor voting algorithm is used to alleviate the problem of local broken roads and enhance the outputs at the postprocessing stage.
2.1. The Structure of the Refined Deep Residual Convolutional Neural Network
The RDRCNN architecture is an end-to-end symmetric training structure to predict pixel-level results and was inspired by ResNet [
25], U Net [
26], and Deeplab [
28]. RDRCNN consists of two core units, including an RCU and a DPU, followed by a full convolution layer.
The architecture is designed with three parts, as shown in
Figure 2. The first part is designed to extract the features using some RCUs (the blue blocks shown on the left of
Figure 2) with a shrinking structure via some max-pooling operators. The second part at the bottom of
Figure 2 (orange blocks) is for enlarging the field of view (FOV) without losing resolution by using consecutive multi-scaled dilated connected units. The third part is an extensive structure for generating a road extraction map that is the same size as the input.
The basic components of each unit usually consist of different operators, including convolution (dilated convolution, full convolution [
29], etc.), nonlinear transformation (ReLU, sigmoid, etc.), pooling (max-pooling, average-pooling, etc.), dropout, concatenate and batch normalization. The convolution produces new features, each element of which is obtained by computing a dot product between the FOV and a set of weights (convolutional kernels). The convolution layer needs to be activated by a nonlinear function to improve its expression capability. However, the repeated combination of max-pooling and striding at consecutive layers of these networks significantly reduces the spatial resolution of the resulting feature maps. A partial remedy is to use the up-sampling layer, which requires additional memory and time. Because of the characteristics of remote sensing imagery (e.g., large cover regions, high resolution, complex backgrounds), a deeper network structure can theoretically gain more effective information for the goal task. However, the exploding gradient problem and vanishing gradient problem may occur [
30]. Therefore, an RCU and a multi-scaled DPU based on [
28] and [
31] are used to alleviate these problems, and these units are discussed as follows.
2.1.1. Residual Connected Unit
Residual learning and identity mapping by shortcuts were first proposed in [
25]. This procedure exhibits good performance in the field of computer vision. In [
25], the building block was defined by the equation below:
where
and
are the output and input vectors of the considered layers, respectively. The function
represents ReLU [
32], and the biases are omitted to simplify the notations. Equation (1) is performed by a shortcut connection and elementwise addition. Then, the second activation function is followed by the addition. He et al. [
25] presented a detailed discussion of the impacts of different combinations and suggested a full pre-activation design. In this paper, the shortcut connected unit is modified as shown in
Figure 3, whose details are depicted in
Table 1. To prevent the overfitting gap, we add the batch normalized layer [
33] to the bottom of the basic unit.
2.1.2. Dilated Perception Unit
To satisfy both the large receptive field and the high spatial resolution, we adopt dilated convolution [
31]. The dilated convolutions enlarge the receptive field while maintaining the resolution [
34]. As shown in
Figure 4, a DPU consists of the dilated convolution layer and the full convolution layer. The former utilizes specific kernels with sparsely aligned weights to enlarge the FOV, and the latter retains the relationships among the neighborhood. Both kernel size and the interval of sparse weights expand exponentially with the increase in the dilation factor. By increasing the dilation factor, the FOV also expands exponentially [
35].
In this paper, we design four scales for the DPUs, as done in a previous study [
31]. Details of the experimental parameters are described in
Table 2.
2.2. Postprocessing
RDRCNN detects road regions but does not guarantee continuous road regions, especially around road intersections. However, it can lead to broken roads that were blocked by shadows or trees in the RDRCNN outputs. To solve address this disadvantage, a postprocessing step is used to reduce broken regions and improve topology expression.
In this work, the tensor voting (TV) algorithm [
36], which is a blind voting method between voters, is used in postprocessing. In this paper, the algorithm implements the smoothness constraint to generate descriptions in terms of regions from RDRCNN outputs. The method is based on tensor calculus for representation and linear voting for communication [
37].
• Encoding the RDRCNN outputs into tensors
First, a second-order symmetric semipositive tensor is used to encode the data of the predicted structures in the input image. In this section, these tensors can be visualized as ellipses [
37]. A second-order symmetric tensor T in 2D can be represented as a nonnegative definite 2 × 2 symmetric matrix, which can be generated by the following equation:
where
and
are the eigenvectors of
, and
and
are their respective eigenvalues.
describes a stick tensor, and
describes a ball tensor.
• Fundamental stick voting field and stick votes
Second, while voting, tensors cast votes in different positions along the space. The votes constitute the voting field of a tensor at every location. During TV, the direction of each tensor is cast as a vote at a certain site that has a normal along the radius of the osculating circle that connects the voter with the vote location, as illustrated in
Figure 5. This condition comes out of the observation that the osculating circle represents a smooth continuation of an oriented feature. The received vote is rotated at an angle of 2θ with respect to the voter. The original formulation crops the votes at outside locations (
).
The vote of the broken road region descends with distance along the osculating circle to reduce the correlation between positions that are far apart. The decay function is described in the following equation:
where
denotes the arc length along the osculating circle,
represents the curvature, which can be computed after
,
is the scale parameter, and
controls the decay of the field with curvature, which can be optimally adjusted as a function of the scale parameter
. The expression is described as Equation (4).
The vote SV cast by a stick tensor
T at position
is then expressed as Equation (5):
where
is a rotation matrix for an angle
. The voting tensor is rotated and scaled following the decay function to produce the vote at a position in space.
• Ball votes
The ball voting field can be computed by integrating the votes of a rotating stick. It is assumed that
is a unitary stick tensor oriented in the direction
in polar coordinates. Let this tensor have two degrees of freedom in its orientation that represent
and
. The vote cast by a ball
B can then be described as follows:
where
is the surface of a unitary sphere,
is any of the eigenvalues of
B, and SV is defined in Equation (5).
• Tensor decomposition
As shown in equitation (2), refined tensors are decomposed into stick and ball components by a general saliency tensor. To improve the connectivity of the RDRCNN outputs, the curvature is expressed by for the tangent orientation by for curve saliency.
• Voting collection and constraints with the RDRCNN results
Votes are collected by tensorial addition, which is equivalent to adding the matrix representations of the votes. The outputs and salient features are added and subtracted to detect the location of broken roads. Then, a morphology algorithm is used to thicken the outputs to the same size as their neighborhood.