Fusion of Multispectral and Panchromatic Images via Spatial Weighted Neighbor Embedding
Abstract
:1. Introduction
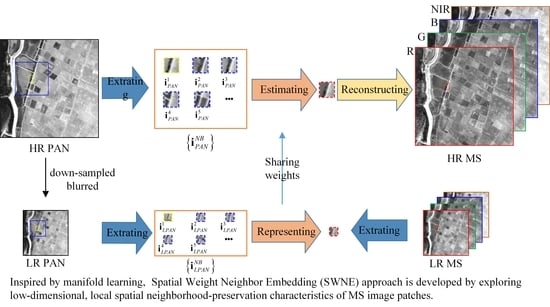
2. Spatial Weighted Neighbor Embedding (SWNE) for Image Fusion
2.1. Spatial Weighted Neighbor Embedding (SWNE)
2.2. Multispectral (MS) and Panchromatic (PAN) Images Fusion Based on SWNE
3. Experiments Results and Analysis
3.1. Datasets and Experimental Conditions
3.2. Evaluation Indexes
3.3. Investigation of SWNE
3.4. Investigation of
3.5. Investigation of Patch Size and Window Size
3.6. Experiments on Reduced-Scale Datasets
3.7. Experiments on Full-Scale Datasets
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2019, 57, 574–586. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Wang, N.; Cen, Y. Joint sparse and low-rank multi-task learning with extended multi-attribute profile for hyperspectral target detection. Remote Sens. 2019, 11, 150. [Google Scholar] [CrossRef]
- Yin, H. Sparse representation based pansharpening with details injection model. Signal Process. 2015, 113, 218–227. [Google Scholar] [CrossRef]
- Javan, F.D.; Samadzadegan, F.; Reinartz, P. Spatial quality assessment of pan-sharpened high resolution satellite imagery based on an automatically estimated edge based metric. Remote Sens. 2013, 5, 6539–6559. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, D.M.; Garzelli, A.; Licciardi, A.G.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Chavez, P.S.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data: Landsat TM and SPOT Panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 265–303. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening, Eastman Kodak Company. U.S. Patent 6011875, 4 January 2000. [Google Scholar]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2012, 3, 177–186. [Google Scholar] [CrossRef]
- Strait, R.S.; Merkurjev, M.D.; Moeller, M.; Wittman, T. An adaptive IHS pan-sharpening method. IEEE Geosci. Remote Sens. Lett. 2010, 7, 746–750. [Google Scholar]
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image fusion—The ARSIS concept and some successful implementation schemes. ISPRS J. Photogramm. Remote Sens. 2003, 58, 4–18. [Google Scholar] [CrossRef]
- Pradhan, P.S.; King, R.L.; Younan, N.H.; Holcomb, D.W. Estimation of the number of decomposition levels for a wavelet-based multiresolution multisensor image fusion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3674–3686. [Google Scholar] [CrossRef]
- Zheng, S.; Shi, W.Z.; Liu, J.; Tian, J. Remote sensing image fusion using multiscale mapped LS-SVM. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1313–1322. [Google Scholar] [CrossRef]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Kahaki, S.M.M.; Jan, N.M.; Ashtari, A.H.; Zahra, J.S. Deformation invariant image matching based on dissimilarity of spatial features. Neurocomputing 2016, 175, 1009–1018. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef]
- Wang, W.; Jiao, L.; Yang, S. Fusion of multispectral and panchromatic images via sparse representation and local autoregressive model. Inf. Fusion 2014, 20, 73–87. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, H.; Gong, W.; Zhang, H. Adjustable model-based fusion method for multispectral and panchromatic images. IEEE Trans. Syst. Man Cybern. B Cybern. 2012, 42, 1693–1704. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Wang, M.; Yang, S.; Xing, Y.; Qu, R. Fusion of panchromatic and multispectral images via coupled sparse non-negative matrix factorization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5740–5747. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. A new pan-sharpening method using a compressed sensing technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 736–746. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Remote sensing image fusion via sparse representations over learned dictionaries. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4779–4789. [Google Scholar] [CrossRef]
- Yin, H. A joint sparse and low-rank decomposition for pansharpening of multispectral images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4779–4789. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, K.; Wang, M. Learning low-rank decomposition for pan-sharpening with spatial-spectral offsets. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3647–3657. [Google Scholar] [PubMed]
- Schultz, R.R.; Stevenson, R.L. Extraction of high-resolution frames from video sequences. IEEE Trans. Image Process. 1996, 5, 996–1011. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.-W. Nonlocal tensor sparse representation and low-rank regularization for hyperspectral image compressive sensing reconstruction. Remote Sens. 2019, 11, 193. [Google Scholar] [CrossRef]
- Ying, H.; Leung, Y.; Cao, F.; Fung, T.; Xue, J. Sparsity-based spatiotemporal fusion via adaptive multi-band constraints. Remote Sens. 2018, 10, 1646. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Xie, X.; Li, Y. Salient object detection via recursive sparse representation. Remote Sens. 2018, 10, 652. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, M.; Cao, Z.; Pi, Y. SAR image recognition with monogenic scale selection-based weighted multi-task joint sparse representation. Remote Sens. 2018, 10, 504. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Hu, Z.; Ye, R. Self-dictionary regression for hyperspectral image super-resolution. Remote Sens. 2018, 10, 1574. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Convolution structure sparse coding for fusion of panchromatic and multispectral images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1117–1130. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. A sparse image fusion algorithm with application to pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2827–2836. [Google Scholar] [CrossRef]
- Zhu, X.X.; Grohnfeldt, C.; Bamler, R. Exploiting joint sparsity for pansharpening: The J-SparseFI algorithm. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2664–2681. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, H.; Shen, H.; Zhang, L. Two-step sparse coding for the pan-sharpening of remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1792–1805. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, K.; Pan, X.; Yang, S. Sparse tensor neighbor embedding based pan-sharpening via N-way block pursuit. Knowl. Based Syst. 2018, 149, 18–33. [Google Scholar] [CrossRef]
- Caiafa, C.; Cichocki, A. Block sparse representations of tensors using Kronecker bases. IEEE Trans. Geosci. Remote Sens. 2012, 7, 1–5. [Google Scholar]
- Lin, T.; Zha, H. Riemannian manifold learning. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 796–807. [Google Scholar] [PubMed]
- Chang, H.; Yeung, D.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2004), Washington, DC, USA, 27 June–2 July 2004; pp. 1–9. [Google Scholar]
- Zhang, K.; Wang, M.; Yang, S. Multispectral and hyperspectral image fusion based on group spectral embedding and low-rank factorization. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1363–1371. [Google Scholar] [CrossRef]
- Sun, L.; Zhan, T.; Wu, Z.; Xiao, L.; Jeon, B. Hyperspectral mixed denoising via spectral difference-induced total variation and low-rank approximation. Remote Sens. 2018, 10, 1956. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Saul, L.K.; Roweis, S.T. Think globally, fit locally: Unsupervised learning of low dimensional manifolds. J. Mach. Learn. Res. 2003, 4, 119–155. [Google Scholar]
- Yu, H.; Gao, L.; Liao, W.; Zhang, B. Group Sparse representation based on nonlocal spatial and local spectral similarity for hyperspectral imagery classification. Sensors 2018, 18, 1695. [Google Scholar] [CrossRef] [PubMed]
- Ehsan, E.; Vidal, R. Sparse manifold clustering and embedding. In Proceedings of the Advances in Neural Information Processing Systems 24 (NIPS 2011), Granada, Spain, 12–15 December 2011; pp. 1–9. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Treads Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Kahaki, S.M.M.; Arshad, H.; Nordin, M.J.; Ismail, W. Geometric feature descriptor and dissimilarity-based registration of remotely sensed imagery. PLoS ONE 2018, 13, 0200676. [Google Scholar] [CrossRef] [PubMed]
- Fraser, C.; Ravanbakhsh, M. Georeferencing performance of Geoeye-1. Photogramm. Eng. Remote Sens. 2009, 75, 634–638. [Google Scholar]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A fast Intensity–Hue–Saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Otazu, X.; Audicana, G.M.; Nunez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef] [Green Version]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Rodriguez-Esparragon, D.; Marcello-Ruiz, J.; Medina-Machín, A.; Eugenio-Gonzalez, F.; Gonzalo-Martín, C.; Garcia-Pedrero, A. Evaluation of the performance of spatial assessments of pansharpened images. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1619–1622. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the 4th JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Xiao, C.; Liu, M.; Nie, Y.; Dong, Z. Fast exact nearest patch matching for patch-based image editing and processing. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1122–1134. [Google Scholar] [CrossRef] [PubMed]












| Metric | GIHS [49] | PCA [6] | AWLP [50] | SVT [13] | SparseFI [32] | NE | SWNE |
|---|---|---|---|---|---|---|---|
| CC | 0.8700 | 0.8563 | 0.8642 | 0.8705 | 0.8798 | 0.8830 | 0.8909 |
| Q4 | 0.8187 | 0.6741 | 0.8019 | 0.7932 | 0.8328 | 0.7943 | 0.8276 |
| FC | 0.9730 | 0.9701 | 0.9778 | 0.9713 | 0.9750 | 0.9759 | 0.9790 |
| SAM | 9.7731 | 9.8995 | 10.6052 | 9.7133 | 9.4060 | 9.2355 | 9.1420 |
| ERGAS | 4.3984 | 5.3566 | 4.4717 | 4.4366 | 4.1915 | 4.2329 | 4.0089 |
| Metric | GIHS [49] | PCA [6] | AWLP [50] | SVT [12] | SparseFI [32] | NE | SWNE |
|---|---|---|---|---|---|---|---|
| CC | 0.9670 | 0.9632 | 0.9687 | 0.9693 | 0.9699 | 0.9691 | 0.9715 |
| Q4 | 0.8939 | 0.8571 | 0.8965 | 0.8982 | 0.9021 | 0.8783 | 0.8834 |
| FC | 0.9798 | 0.9718 | 0.9850 | 0.9839 | 0.9791 | 0.9841 | 0.9854 |
| SAM | 4.1535 | 3.4104 | 4.7313 | 4.4978 | 4.2024 | 4.2186 | 4.0642 |
| ERGAS | 1.6761 | 1.7801 | 1.5507 | 1.5272 | 1.5033 | 1.5437 | 1.4631 |
| Metric | GIHS [49] | PCA [6] | AWLP [50] | SVT [12] | SparseFI [32] | NE | SWNE |
|---|---|---|---|---|---|---|---|
| FC | 0.9519 | 0.9508 | 0.9679 | 0.9662 | 0.9599 | 0.9565 | 0.9690 |
| 0.0820 | 0.0875 | 0.0669 | 0.0659 | 0.0476 | 0.0784 | 0.0838 | |
| 0.0909 | 0.0977 | 0.0777 | 0.0843 | 0.0976 | 0.0678 | 0.0609 | |
| QNR | 0.8346 | 0.8322 | 0.8606 | 0.8562 | 0.8594 | 0.8591 | 0.8604 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, F.; Yang, S. Fusion of Multispectral and Panchromatic Images via Spatial Weighted Neighbor Embedding. Remote Sens. 2019, 11, 557. https://doi.org/10.3390/rs11050557
Zhang K, Zhang F, Yang S. Fusion of Multispectral and Panchromatic Images via Spatial Weighted Neighbor Embedding. Remote Sensing. 2019; 11(5):557. https://doi.org/10.3390/rs11050557
Chicago/Turabian StyleZhang, Kai, Feng Zhang, and Shuyuan Yang. 2019. "Fusion of Multispectral and Panchromatic Images via Spatial Weighted Neighbor Embedding" Remote Sensing 11, no. 5: 557. https://doi.org/10.3390/rs11050557
APA StyleZhang, K., Zhang, F., & Yang, S. (2019). Fusion of Multispectral and Panchromatic Images via Spatial Weighted Neighbor Embedding. Remote Sensing, 11(5), 557. https://doi.org/10.3390/rs11050557